变化检测是利用不同时期的观测确定地物或现象变化的过程[1-2]。遥感影像具有覆盖面积大、获取周期短的特点,是一种重要的变化检测数据源,在土地利用/覆盖变化检测[3]、城市扩张监测[4]、地形图更新[5]等领域中应用广泛。
遥感影像变化检测依据数据源划分,可分为影像-影像法与矢量-影像法两类[6]。影像-影像法以时序遥感影像为数据源,采用一定的相似性测度衡量影像间的差异,在一定阈值基础上进行变化检测。经典的影像-影像法有影像差值法[7]、影像比值法[8]、变化向量分析法[9]、分类后比较法[10]。矢量-影像法以矢量图与遥感影像作为数据源。现有的矢量-影像法可以划分为分类后比较法与类别特征法两类。分类后比较法将矢量图套合在遥感影像上,提取类别不变的像斑作为训练样本,对遥感影像进行监督分类,并通过比较矢量图类别与分类结果进行变化检测[11-12];类别特征法将矢量图套合在遥感影像上,提取各类别像斑在遥感影像上的特征,以类别为单位分析像斑的特征规律,从中找出发生变化的像斑,并综合各类别的变化结果实现变化检测[13]。
现有矢量-影像法的研究相对较少,且已有的类别特征法对局部变化像斑的检测效果较差,因此本文提出一种基于类别的矢量图与遥感影像变化检测方法。该方法在矢量图约束下对遥感影像进行分割,在影像分割结果的基础上构建像斑的类别异质度,逐类别对像斑进行变化/未变化判别,能够有效检测发生局部变化的像斑,同时实现变化检测的自动化。
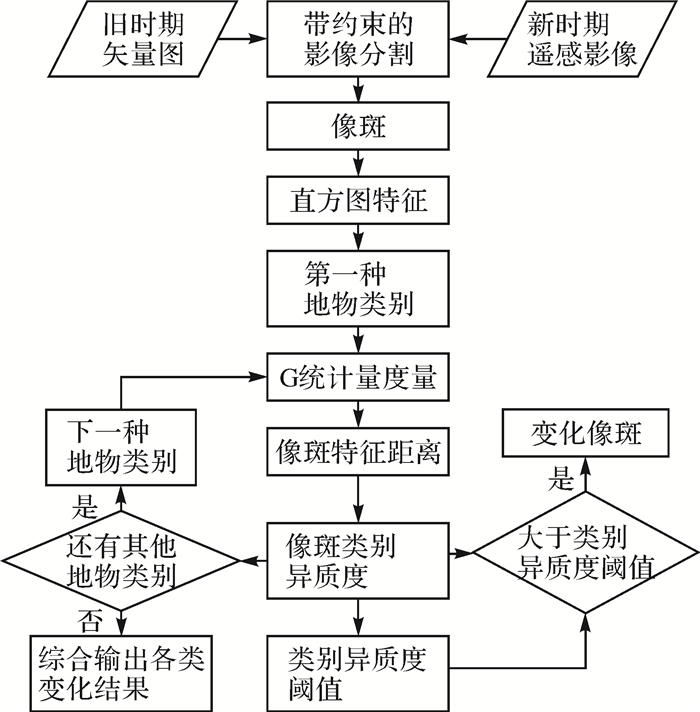
1 本文方法本文方法属于矢量-影像法中的类别特征法,方法流程如图 1所示。
|
| 图 1 本文方法流程 |
以矢量图为约束,对遥感影像进行分割获取像斑;提取直方图作为像斑的特征,采用G统计量度量像斑的特征距离;利用像斑与同类别像斑的特征距离计算单波段上像斑的类别异质度,依据像斑各波段上的信息熵自适应确定各波段的权重,加权组合各波段上像斑的类别异质度构建像斑的类别异质度;采用最大熵法获取各地物类别对应的异质度阈值,以类别为单位,比较该类下各像斑的类别异质度与该类的异质度阈值,实现该类中变化像斑的检测,综合各类的变化检测结果得到完整的变化检测结果。
1.1 带约束的影像分割矢量图中多边形的变化分为全局变化与局部变化两种。全局变化是多边形整体类别发生了改变,局部变化是多边形局部区域发生了改变。为了有效检测矢量图中发生局部变化的区域,需要在矢量图约束下对遥感影像进行分割,将局部变化的区域分割出来。
矢量图约束下的影像分割既要保留原始的矢量图边缘,又要产生影像中新的边缘。常用的带约束影像分割方法通过栅矢套合将矢量图与遥感影像叠加,然后以矢量图中的多边形为单位,对各多边形进行非约束的影像分割获取像斑[14]。非约束的影像分割方法包括区域增长法、区域合并法、边缘检测法等。带约束影像分割后获取的像斑包含新时期遥感影像上的特征,还包含旧时期矢量图中的地物类别属性。为了简单,下文中将像斑在历史时期矢量图中的类别简称为像斑的类别。
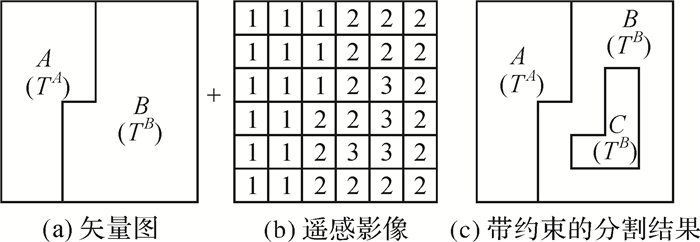
图 2是带约束影像分割的示意图。图 2(a)是矢量图,包含A和B两个多边形,对应的地物类别依次为TA、TB;图 2(b)是遥感影像;图 2(c)是矢量图约束下的遥感影像分割结果。多边形A内部未产生新的边缘,多边形B内部产生了新的多边形C,多边形C在矢量时期对应的地物类别为TB。
|
| 图 2 带约束的影像分割示意图 |
像斑是一系列光谱相似、空间相邻的像元的集合[15]。像斑特征是内部所有像元特征的综合表达,能反映内部像元特征的分布。直方图是一种统计学特征,能够描述变量的分布。灰度直方图用来描述像斑内部像元灰度值及其出现频数的函数关系,可以较好地表达像斑内部像元灰度值的分布,在表达像斑灰度特征的同时,还能在一定程度上表达像斑的纹理特征。灰度直方图可以表示成一张二维图,其横坐标是像元灰度值,纵坐标是灰度值出现的频数。
灰度直方图与灰度级密切相关。灰度级过大,直方图分布过于稀疏,直方图距离度量的准确性会较差,从而降低变化检测的精度;灰度级过小,直方图分布较为紧凑,但会丢失部分细节信息,从而降低变化检测的精度。因此,要在合理的灰度级下提取像斑特征,才能获得最优的变化检测精度。
1.3 像斑特征距离度量利用直方图提取像斑的特征后,像斑的特征距离就转换为直方图距离度量。常用的直方图距离度量方法有G统计量[16-17]、直方图相交距离[18]、相交熵[19]等。文中采用G统计量度量像斑间的特征距离。令两个像斑在第b个波段上归一化直方图分别为fb、hb,其中1≤b≤B,B为遥感影像的波段数,则这两个像斑在该波段上的G统计量如下
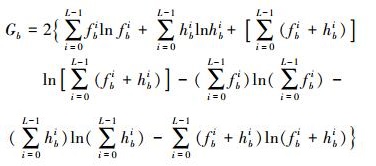 (1)
(1) 式中,Gb表示两个像斑在第b个波段的G统计量;fbi、hbi分别表示两个直方图中灰度值i出现的频率;L表示灰度级。归一化直方图中,所有灰度值的累积频率之和为1,即
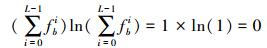 (2)
(2) 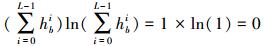 (3)
(3) 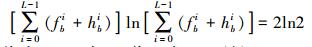 (4)
(4) 将式(2)-式(4) 代入式(1) 可得
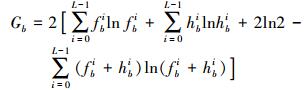 (5)
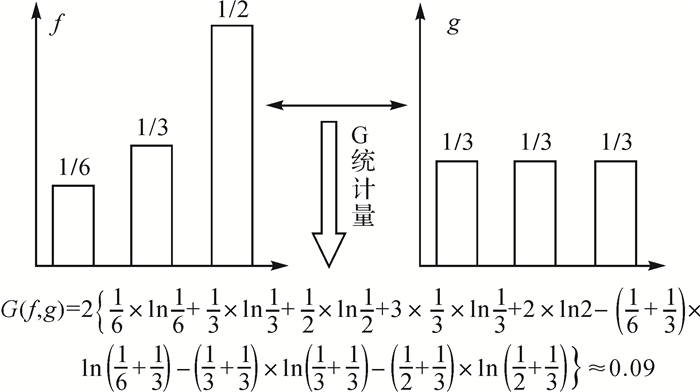
(5) Gb的取值在[0, 4ln2]内。两个像斑直方图的距离越大,则对应的Gb的值越大,反之则越小。当两个直方图完全相同时,Gb取最小值0;当两个直方图不相关时,Gb取最大值4ln2。图 3为两个直方图间G统计量计算的示意图。
|
| 图 3 G统计量计算示意图 |
利用各波段上像斑间G统计量的加权平均值计算像斑的特征距离,即
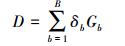 (6)
(6) 式中,Gb、δb分别表示第b个波段的G统计量及其归一化权重值;D为像斑的特征距离。各波段上G统计量权重的确定思想如下:对于某个波段,如果两个像斑中某一个像斑直方图的信息熵较大,表明像斑在该波段中包含更多的信息量,则该波段设定较大的G统计量权重,否则设定较小的权重值。归一化权重的计算如下
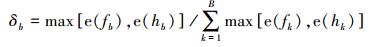 (7)
(7) 式中,e(fb)、e(hb)分别表示直方图fb、hb的信息熵;max()表示取较大值。从式(7) 中可以看出:某个波段上,两个像斑直方图中某个直方图的信息熵较大,则该波段对应G统计量的权重较大;当两个像斑直方图的信息熵均较小时,则该波段对应G统计量的权重较小。
式(7) 中两个直方图信息熵的计算如下
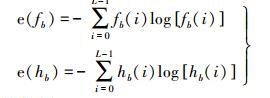 (8)
(8) 像斑直方图的分布越分散,则对应的信息熵越大;分布越集中,则对应的信息熵越小。
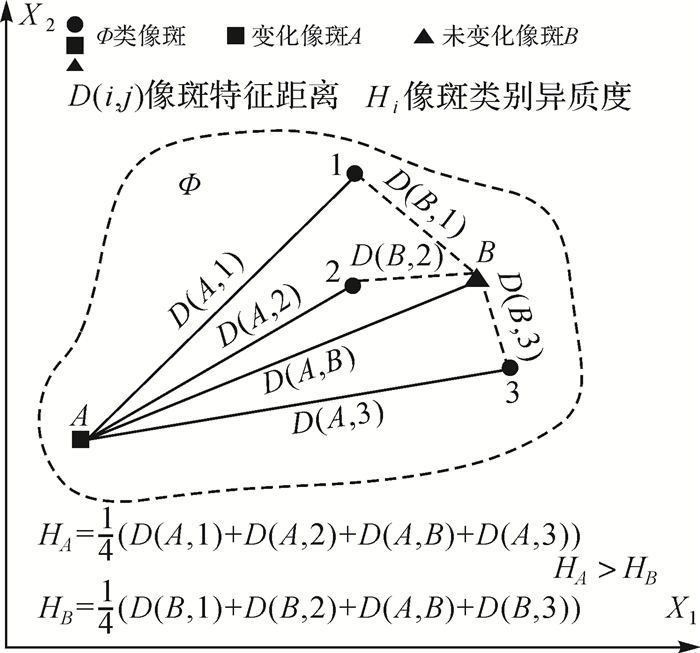
1.4 像斑类别异质度构建像斑类别异质度用来衡量像斑与其所属类别之间的异质度。像斑类别异质度越大,则表明该像斑变化的强度越大。当像斑类别在新时期发生了变化,则该像斑与其他旧时期同类别像斑之间的特征距离较大,对应特征距离的平均值也较大。因此,文中利用像斑与其他同类别像斑之间特征距离的平均值来表达。令Φ类像斑的集合为{Φ1, Φ2, …, Φm},其中m表示该类像斑的个数,Φj(1≤j≤m)表示该类中第j个像斑。像斑Φj的类别异质度计算如下
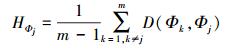 (9)
(9) 式中,HΦj表示像斑Φj的类别异质度;D(Φk, Φj)表示像斑Φk与像斑Φj之间的特征距离。图 4为像斑类别异质度计算的示意图。
|
| 图 4 像斑类别异质度示意图 |
各类像斑中,变化像斑对应的类别异质度较大,未变化像斑对应的类别异质度较小。文中通过设定类别异质度阈值实现各类像斑的变化判别。常用的阈值获取方法有大津法[20]、最大熵法[21]。最大熵法基于熵最大化理论获取最优阈值,不需要预先对数据的分布作任何假设。文中采用最大熵法获取各地物类别对应的阈值。令阈值为λ,Φ类像斑的类别异质度被阈值划分为两类:HΦS={HΦ1S, HΦ2S, …, HΦmsS}与HΦB={HΦ1B, HΦ2B, …, HΦmbB}。其中,HΦS是小于λ的像斑类别异质度集合;ms是对应的像斑个数;HΦB是大于λ的像斑类别异质度集合;mb是对应的像斑个数;m=ms+mb,为Φ类像斑总数。则HΦS、HΦB的信息熵如下
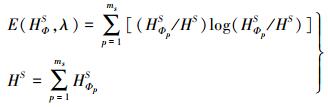 (10)
(10) 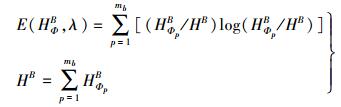 (11)
(11) 式中,E(HΦS, λ)、E(HΦB, λ)分别为在阈值λ下HΦS、HΦB两类的信息熵。Φ类最优的异质度阈值λΦ对应着两类信息熵之和的最大值,即
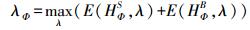 (12)
(12) 每种地物类别均对应一个异质度阈值。各地物类别的异质度阈值取决于该类别所属所有像斑的类别异质度,为此不同的地物类别对应不同的异质度阈值。
1.6 基于类别的像斑变化判别获取各地物类别的异质度阈值后,以类别为单位,对各类地物所属的像斑进行变化判别。Φ类像斑的变化判别如下
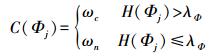 (13)
(13) 式中, Φj表示Φ类中第j个像斑;C(Φj)、H(Φj)分别表示该像斑的变化/未变化类别及类别异质度;λΦ表示Φ类的异质度阈值。
本文变化检测方法的具体流程如下:① 以旧时期矢量图为约束,对新时期遥感影像进行分割获取像斑;② 提取像斑的直方图特征,并利用式(1) 计算单波段上像斑间的直方图距离,采用式(6) 综合各波段的直方图距离计算像斑的特征距离;③ 利用式(9) 逐类计算各像斑的类别异质度,依据式(12) 采用最大熵法计算各地物类别的异质度阈值;④ 比较像斑的类别异质度与对应类别的异质度阈值,采用式(13) 对各像斑进行变化判别。
2 试验及分析文中使用的试验数据为武汉市2002年的土地利用矢量图与2005年的QuickBird遥感影像。2002年土地利用矢量图包含多边形64个,共有道路、耕地、湖泊、居民地、林地、裸地6类地物。遥感影像大小为990×1027像元,包含蓝、绿、红、近红外4个波段,影像空间分辨率为2.4 m。以2002年土地利用矢量图为约束,对2005年遥感影像进行分割,分割后获取像斑219个。为了便于对变化检测结果进行定量评价,采用目视解译的方法制作了标准的地表变化结果。2002-2005年间,武汉城市化进程较快,大量的城市裸地被填平改建为居民地。图 5(a)为2002年土地利用矢量图,图 5(b)为利用QuickBird的红、绿、蓝3个波段合成的2005年真彩色遥感影像,图 5(c)为矢量图约束下的影像分割结果套合在2005年遥感影像上的结果,其中灰色线条表示矢量边界,图 5(d)为地表标准变化结果,其中黑色区域表示变化,白色区域表示未变化。从图 5(c)中可以看出,2002年的许多多边形内部发生了变化,经过带约束的影像分割后,这部分内部边缘被分割出来形成新的多边形,如图 5(c)中黑色箭头指向区域。

|
| 图 5 试验数据 |
文中分别采用正确率、误检率、漏检率3个指标来衡量变化检测的精度。正确率是检测类别与实际类别一致的像元在全部像元中的比例,误检率是实际未变化、检测变化的像元在检测变化像元中的比例,漏检率是实际变化、检测未变化的像元在实际变化像元中的比例。正确率越高,误检率、漏检率越低,则变化检测的精度越高。
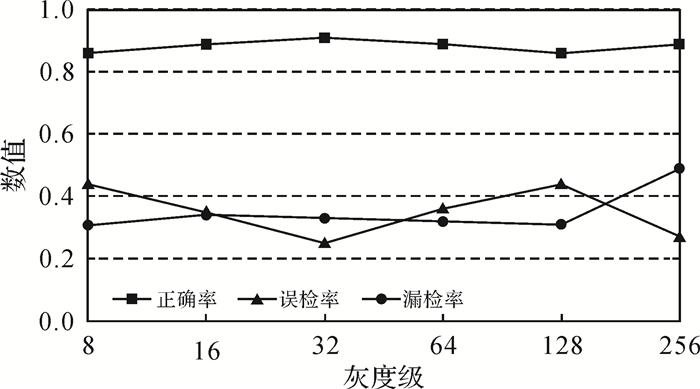
2.1 灰度级试验不同的灰度级对应不同的变化检测结果。为了获取最优的灰度级,文中分别选取了8、16、32、64、128、256共6组灰度级进行变化检测,对应的变化检测如图 6所示。
|
| 图 6 变化检测精度随灰度级变化关系 |
从图中可以看出:当灰度级从8开始增大到32时,正确率呈上升趋势,误检率呈下降趋势,漏检率的波动幅度较小;当灰度级为32时,正确率达到最大值0.91,误检率达到最小值0.25,此时漏检率为0.33;当灰度级从32增大到128时,正确率呈下降趋势,误检率呈上升趋势,漏检率呈微弱下降趋势;灰度级从128增大到256时,正确率及漏检率呈上升趋势,误检率呈下降趋势。当灰度级L=32时,正确率及误检率均为最优,且此时的漏检率为0.33,与最优的漏检率0.31相差较小。因此文中选取灰度级L=32进行变化检测,此时变化检测结果的混淆矩阵见表 1。
| 类别 | 检测未变化 | 检测变化 | 合计 |
| 实际未变化 | 816 092 | 36 742 | 852 834 |
| 实际变化 | 54 695 | 109 201 | 163 896 |
| 合计 | 870 787 | 145 943 | 1 016 730 |
| 正确率/(%) | 91 | ||
| 误检率/(%) | 25 | ||
| 漏检率/(%) | 33 | ||
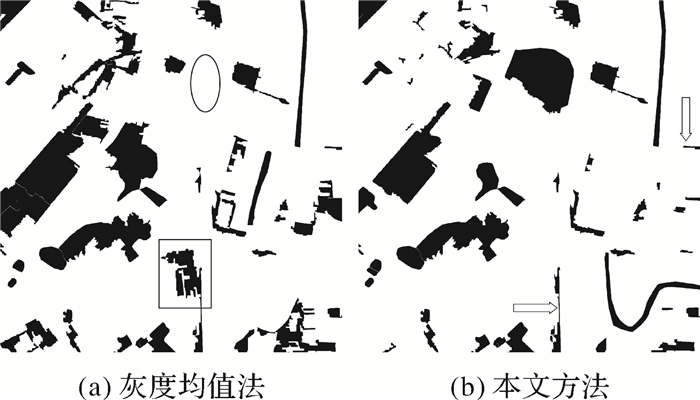
为了验证本文方法的有效性,将本文方法同基于像斑灰度均值的方法进行对比。像斑灰度均值利用像斑内像元的灰度均值表达像斑的特征,利用欧氏距离计算像斑间的特征距离,构建类别异质度后进行变化检测。两种方法的变化检测结果如图 7所示。图中黑色区域表示变化,白色区域表示未变化。
|
| 图 7 不同方法的变化检测结果 |
从图中可以看出:像斑灰度均值法存在大量的误检(图 7(a)中黑色矩形内部区域)与漏检(图 7(a)中黑色椭圆形内部区域)。图 7(a)中椭圆形区域在2002年土地利用矢量图中地物类别为裸地,在2005年遥感影像上变化为居民地,两者的反射率均较强,对应的灰度均值均较大且相差较小,两者之间的特征距离较小,导致裸地像斑的类别异质度较小,从而产生漏检;图 7(a)中矩形区域在2002年土地利用矢量图中地物类别为居民地,由于居民地的多样性,不同类型居民地之间的灰度均值会相差较大,对应的特征距离也较大,导致居民地像斑的类别异质度较大,从而产生误检。图 7(b)的变化检测精度较好,图 7(a)中部分误检及漏检的区域均能得到正确检测。这是因为利用直方图表达像斑特征后,一方面可以增大不同类别地物之间的特征距离,另一方面可以减小相同类别地物之间的特征距离,构建的像斑类别异质度能够合理表达像斑的变化大小,从而提高了变化检测的精度。然而本文方法会将部分线状像斑误判为变化(图 7(b)中箭头指向区域),这是因为线状像斑包含的像元数较少,导致像斑直方图较为稀疏,影响了直方图距离度量的准确性,从而导致误检和漏检。
两种方法变化检测结果的精度对比见表 2。
从表 2中可以看出:灰度均值法的误检率及漏检率均较高,本文方法的各项精度均优于灰度均值法。
3 结论矢量-影像法是一种重要的变化检测方法。矢量图不仅包含地物的空间位置信息,还包括了地物的类别信息。本文提出了一种基于类别的矢量图与遥感影像的变化检测方法,实现了变化检测的自动化。通过矢量图约束的影像分割获取像斑,提取像斑的直方图特征,采用G统计量计算像斑的特征距离,利用像斑及同类别像斑特征距离的平均值构建像斑的类别异质度,依据最大熵法获取各地物类别对应的异质度阈值,比较像斑的类别异质度及对应类别的异质度阈值实现像斑的变化判别。在QuickBird遥感影像上的试验验证了本文方法的有效性,同时可以得出以下结论:
(1) 利用直方图提取像斑特征时,直方图的灰度级应适中。灰度级过大,直方图过于稀疏,会降低直方图距离度量的准确性,降低变化检测的精度;灰度级过小,直方图较为紧凑,但会丢失部分地物细节信息,减小地物之间的可分性,导致变化检测中的漏检。
(2) 本文方法能够实现矢量图与遥感影像变化检测的自动化。不需要人工选取训练样本,采用自动的阈值获取方法,因此能够实现自动化的变化检测,提高变化检测的效率。
(3) 本文方法的适用前提为各类地物下发生变化的像斑比例较小。当某类地物下发生变化的像斑较多,并朝着同一地物类别变化时,会导致变化像斑的类别异质度较小,未变化像斑的类别异质度反而较大,从而导致错误的变化检测结果。
如何去除或弱化本文方法的适用前提是下一阶段研究工作的重点。
| [1] | SINGH A. Review Article Digital Change Detection Techniques Using Remotely-sensed Data[J]. International Journal of Remote Sensing, 1989, 10(6): 989–1003. DOI:10.1080/01431168908903939 |
| [2] | 吴炜, 沈占锋, 吴田军, 等. 联合概率密度空间的遥感自适应变化检测方法[J]. 测绘学报, 2016, 45(1): 73–79. |
| [3] | 佃袁勇, 方圣辉, 姚崇怀. 多尺度分割的高分辨率遥感影像变化检测[J]. 遥感学报, 2016, 20(1): 129–137. |
| [4] | 王琳, 徐涵秋, 李胜. 福州城市扩展的遥感动态监测[J]. 地球信息科学学报, 2006, 8(4): 129–135. |
| [5] | 赵敏, 陈卫平, 王海燕. 基于遥感影像变化检测技术的地形图更新[J]. 测绘通报, 2013(4): 65–67. |
| [6] | 李德仁. 利用遥感影像进行变化检测[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 7–12. |
| [7] | BRUZZONE L, PRIETO D F. Automatic Analysis of the Difference Image for Unsupervised Change Detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(3): 1171–1182. DOI:10.1109/36.843009 |
| [8] | 王桂婷, 王幼亮, 焦李成. 自适应空间邻域分析和瑞利-高斯分布的多时相遥感影像变化检测[J]. 遥感学报, 2009, 13(4): 639–646. DOI:10.11834/jrs.20090407 |
| [9] | VARSHNEY A, ARORA M K, GHOSH J K. Median Change Vector Analysis Algorithm for Land-use Land-cover Change Detection from Remote-sensing Data[J]. Remote Sensing Letters, 2012, 3(7): 605–614. DOI:10.1080/01431161.2011.648281 |
| [10] | 李雪, 舒宁, 王琰, 等. 利用土地利用状态转移分析的变化检测[J]. 武汉大学学报(信息科学版), 2011, 36(8): 952–955. |
| [11] | WALTER V. Object-based Classification of Remote Sensing Data for Change Detection[J]. ISPRS Journal of photogrammetry and Remote Sensing, 2004, 58(3): 225–238. |
| [12] | 张继贤, 杨贵军. 单一时相遥感数据土地利用与覆盖变化自动检测方法[J]. 遥感学报, 2005, 9(3): 294–299. DOI:10.11834/jrs.20050343 |
| [13] | 谢仁伟, 牛铮, 孙睿, 等. 基于多波段统计检验的土地利用变化检测[J]. 国土资源遥感, 2009, 21(2): 66–70. DOI:10.6046/gtzyyg.2009.02.14 |
| [14] | 袁媛, 刘顺喜, 陈静波, 等. 土地利用现状图斑约束下的并行图像分割[J]. 国土资源遥感, 2013, 25(4): 160–165. DOI:10.6046/gtzyyg.2013.04.26 |


