常见的单面阵数码相机影像存在视场角窄、像幅小等常见问题,而全景影像则具有超大视场角、超强立体感和真实感、旋转不变性及成像一体化等显著特点[1-3],可以使人们更加直观、快捷、全面地建立对周围环境的整体认识。全景影像技术目前已被广泛应用到街景地图制作、测绘、旅游、交通、数字城市建设等多个领域[4-6],全景影像与激光点云数据的融合是目前数字城市三维信息的重要表达形式之一[6-8],全景相机逐渐成为车载移动测量系统中必不可少的重要传感器之一。车载全景相机一般是由多台单面阵数码相机按照一定的几何结构集成在一起的(如Ladybug系列全景相机),通过单相机间的同步曝光获取周围场景的影像,然后经过影像拼接与融合形成全景影像[2, 7-9]。
全景影像的质量主要受单影像质量和影像拼接方法的影响,常用的全景影像拼接方法有基于影像匹配的方法和基于全景相机标定参数的拼接方法[10];顾忌影像采集方式、拼接速度、效率、质量和后续应用等因素的综合影响,车载全景影像的生成一般采用后一种方法。文献[11]提出了一种全景相机的严格成像模型;文献[8, 12]对多拼全景相机的理想成像模型和严格成像模型进行了定位精度比较,得出严格成像模型的全景影像定位精度要高于理想成像模型,并推荐采用严格成像模型,特别是对自主集成的多拼全景相机。无论是理想成像模型,还是严格成像模型均需提供全景相机的标定参数才能完成全景影像的拼接,标定参数的精度是影响全景影像拼接效果和几何量测精度的重要因素之一,因此,全景相机的精确标定是生成车载全景影像必不可少的关键步骤之一。
国内外学者对全景相机的标定方法进行了相关研究。如文献[13]采用不同摄影距离的标定板完成了Ladybug全景相机的标定;文献[4]提出了一种借助三维激光扫描数据提供的特征点作为控制点,然后利用单张影像完成全景相机标定的方法。在没有理想标定场的情况下,本文提出一种利用物方少量控制点和多个摄影方向的多张影像联合进行光束法空三平差完成全景相机严密标定的方法,推导了平差的数学模型,并进行了相关标定试验验证。
1 标定场建立全景相机中相邻相机间的摄影重叠度一般较小,因此一般需要借助物方足够数量的高精度控制点辅助完成全景相机内参数的几何标定。由于室内具有稳定、不易受天气影响、易于长期保存和可多次重复利用等优势,本文利用现有资源,将全景相机标定场布设在一个长×宽×高约为52 m×20 m×12 m、采光效果相对较好的实验室内,如图 1所示。

|
| 图 1 全景相机标定场 |
人工标志点主要选用了铝合金材质的黑白色“宝马标”图案,地面上部分临时点采用了不干胶材质。由于室内白色墙壁纹理特征匮乏,为保证标定时能够获取足够数量的影像连接点,以及满足其他不同目的的应用需求,在室内不同景深位置的四周墙壁、顶部和地面均匀布设了约1000个人工标志点,并采用徕卡TM5100A工业测量系统进行标志点物方坐标测量,所有标志点坐标统一后最差点位精度不大于0.3 mm。
2 标定原理标定流程如图 2所示。
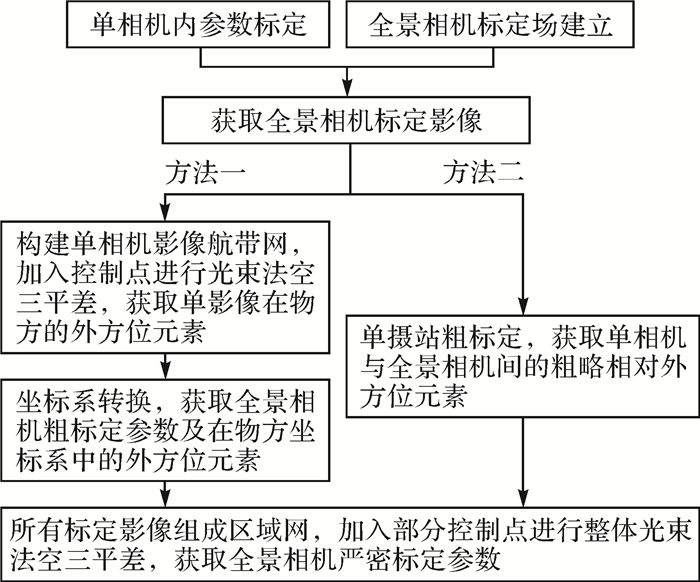
|
| 图 2 全景相机严密标定流程 |
全景相机标定过程中涉及物方和像方两类坐标系,各坐标系定义如下:
(1) 单相机像平面坐标系o-xy。x轴平行于像片的上下边,指向像片的右侧,y轴垂直于x轴向上,坐标系原点位于像片主点。
(2) 单相机像空间坐标系S-xyz。Sx轴平行于像平面坐标系的x轴,Sz轴平行于像平面坐标系的y轴,Sy轴指向像主点。
(3) 单相机像空间辅助坐标系S-x′y′z′。坐标轴的朝向和全景相机辅助坐标系的朝向一致,坐标系原点位于摄影中心。
(4) 全景相机坐标系S全-X全Y全Z全。坐标原点S全取单相机摄影中心的几何重心,S全-X全Y全面与单相机摄影中心基本处于同一平面内,根据全景相机在移动平台中的安装方位确定坐标系三轴的朝向。
(5) 物方坐标系O-XYZ。坐标原点和朝向根据测量时的测站情况而定,Z轴垂直于地面朝上。
(6) 全景相机辅助坐标系S全-X′全Y′全Z′全。坐标系原点与全景相机坐标系原点相同,3个坐标轴平行于物方坐标系的三轴,朝向相同。
除像平面坐标系为二维平面直角坐标系外,其余坐标系均为右手空间直角坐标系。如图 3所示。
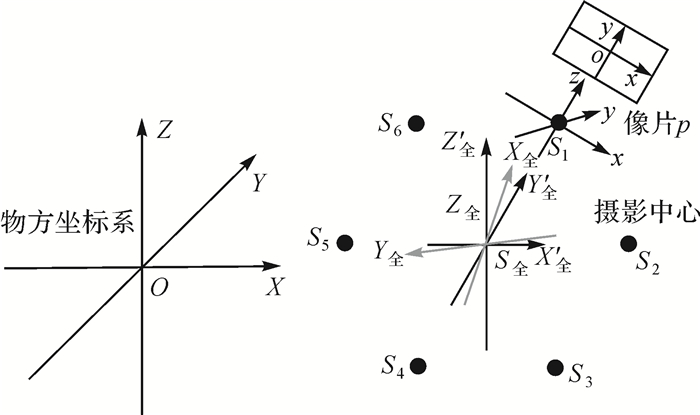
|
| 图 3 坐标系示意图 |
组成全景相机的单相机一般采用非量测型工业数码相机,为保证影像的几何量测精度,整体标定前其内方位元素和各项畸变参数必须进行检校。单相机标定前,首先要根据全景相机作业时大概的摄影距离对单相机进行调焦至清晰状态并固定焦距,然后对室内高精度三维数码相机标定场进行摄影获取所需标定影像,利用空间后方交会原理进行单相机内参数的标定[14], 详细标定过程此处不再详述。
2.3 全景相机标定全景相机一般是按照事先设计好的位置和姿态将所有单相机固定在同一平台上,通过相机之间的同步曝光控制完成全景影像的采集。但由于机械设计、加工和安装误差的存在,以及单相机摄影中心和像片姿态的不可见性,致使全景相机组装完成后,单相机之间的精确相对位置关系未知,因此全景相机组装后必须进行全景相机的精确标定,以便为全景影像的拼接、量测等应用提供准确的参数。
文中将全景相机的标定分为粗标定和严密标定两部分,最终目的是获取每台单相机像空间坐标系与全景相机坐标系之间的6个坐标转换参数,即每台单相机在全景坐标系中的3个线元素(ΔXSj ΔYSj ΔZSj)和3个角元素(Δφj Δωj Δκj),组成旋转矩阵ΔRj。
2.3.1 粗标定粗标定的目的是获取单相机之间的粗略相对方位元素,为严密标定平差提供初始值。在物方坐标系O-XYZ中,全景相机坐标系原点S全的物方坐标为
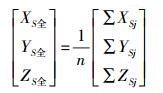 (1)
(1) 式中,n为组成全景相机的单相机个数;j为单相机的序号;(XSj YSj ZSj)为单相机摄影中心在物方坐标系中的位置。单相机摄影中心与全景相机坐标系原点之间的坐标差为
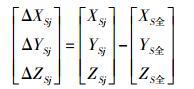 (2)
(2) 假设全景相机坐标系的三轴与其中的5号单相机(为方便公式表达,根据实际需要选择轴向)的像空间坐标系三轴朝向相同,由式(1) 和式(2) 联合推算待求标定参数中的线元素为
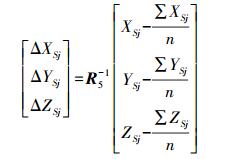 (3)
(3) 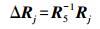 (4)
(4) 式(3) 中,R5-1为5号单相机像空间坐标系与物方坐标系间的旋转矩阵的逆矩阵。式(4) 中,ΔRj为待求单相机像空间坐标系与全景相机坐标系间的旋转矩阵;Rj为单相机像空间坐标系与物方坐标系间的旋转矩阵。
若全景相机的标定只采用单个曝光点位置的标定影像,利用物方和像方相对应的一定数量的控制点,通过单片后方交会的方法求出每张像片在物方坐标系中的外方位元素后,再利用式(3) 和式(4) 即可解算出全景相机的标定参数。但采用此方法进行全景相机标定时,标定结果的精度易受控制点在单片中的数量、分布等因素的影响,而且现实环境中建立理想的全景相机标定场存在一定难度,因此采用单摄站单片空间后方交会的方法进行多拼全景相机的标定不能保证标定结果的可靠性和精度,文中将其作为粗标定结果使用。
2.3.2 严密标定数学模型多个摄影方向获取的多张影像联合平差,可以有效提高摄影测量解算结果的精度和可靠性。文中提出的全景相机严密标定方法就是以多方向多影像为前提基础,参考航测中空中三角测量的思想,利用影像间的重叠区域建立整体区域网,通过对多张影像联合进行光束法空三平差的方法解算每台单相机在全景坐标系中的方位元素。相对于单摄站影像的标定方法,多方向多影像的全景相机严密标定方法可有效提高标定结果的可靠性和精度,减小对标定场中控制点数量和布设方案的过多依赖,同时多影像的联合平差可以使标定结果更为严密。
单相机影像的空间定位方程为
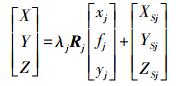 (5)
(5) 式中,[X Y Z]为像点对应的物点的物方坐标;[xj yj]为单相机影像上像点的像平面坐标;fj为单相机影像的像片主距;λi为比例因子;Rj为单相机影像的像空间坐标系与物方坐标系之间的旋转矩阵。
将全景相机作为一个整体,联合式(2)-式(5) 推算全景相机的空间定位方程为
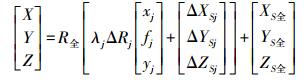 (6)
(6) 式中,R全为全景相机坐标系与物方坐标系间的坐标变换旋转矩阵,由全景相机在物方控制点坐标系中的3个姿态角(φ全 ω全 κ全)构成。令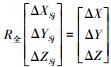
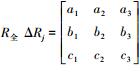
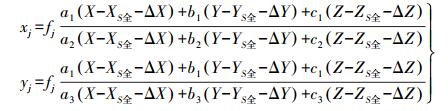 (7)
(7) 参数解算方法一:首先将每台单相机所获取的标定影像建立单相机影像航带网,加入部分控制点进行光束法空三平差,获得单张标定影像在物方坐标系中的6个外方位元素,再利用式(3) 和式(4) 解算出每个摄站点全景相机坐标系在物方坐标系中的位置和姿态;将式(7) 进行线性化,其中,单相机影像上的像点坐标为观测值,物方控制点坐标、全景相机的外方位元素和单相机内参数为已知值,加入部分控制点将所有影像组成的区域网进行整体空三平差,解算全景相机的内标定参数,即每台单相机相对于全景相机的6个方位元素,以及连接点的地面三维坐标。区域网空三平差的误差方程式如下
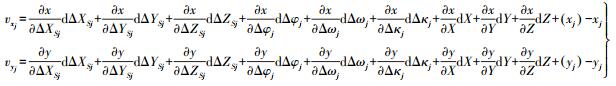 (8)
(8) 参数解算方法二:无需事先解算每张单相机影像在标定场坐标系中的6个外方位元素,而是将所有单影像根据摄影位置参数构建一个整体区域网,加入控制点后进行整体光束法空三平差。将单影像中像点坐标作为观测值,控制点物方坐标和单相机内参数作为已知值,待求量为全景相机在物方的位置和姿态、单相机与全景相机的相对方位元素及连接点的地面三维坐标,对式(7) 进行线性化,建立如下误差方程式
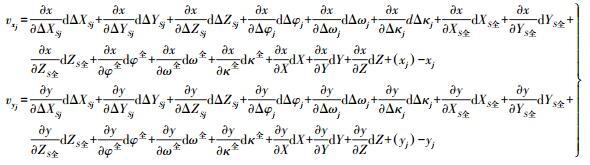 (9)
(9) 方法一中,首先对全景相机中每台单相机获取的标定影像构建单影像航带网并加入控制点进行光束法空三,解算出每张单影像在物方的绝对位置和姿态,然后将所有单影像构建区域网,整体平差解算全景相机的标定参数;方法二中,直接根据摄影参数构建区域网,加入控制点后进行光束法空三。两种方法相比较,方法一的解算流程相对复杂一些,方法二更直接方便;两种方法都利用了多摄站的多张标定影像构建整体区域网进行光束法空三平差,相对于单摄站的标定方法,减少了对控制点的依赖,多方向多影像联合平差解算的全景相机参数更加可靠和严密。
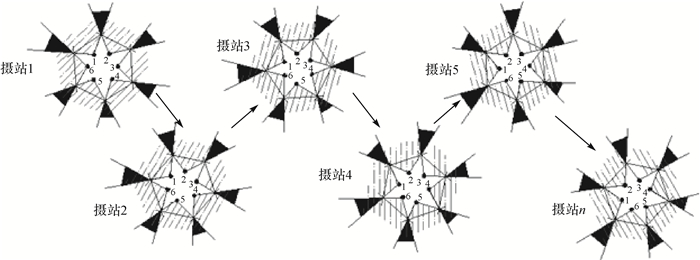
3 试验分析采用由6台PointGrey系列工业相机集成的柱面全景相机进行试验分析,如图 4所示,相邻相机影像间的重叠度约20%左右。将全景相机大致水平固定在一个可移动的小型平台上进行标定影像的采集。考虑到标定场的摄影条件及影像自动化匹配时的理想交会角大致在5°~10°[15-16]的范围内,标定影像采集时,采用多方向旋转摄影的方式,每次旋转的角度保持在10°左右,如图 5所示。

|
| 图 4 多拚柱面全景相机 |
|
| 图 5 标定影像摄影方式示意图 |
将摄影平台放置在标定场大致中间的位置,首先在摄站1进行摄影,之后将摄影平台移向离摄站1的斜前方大约0.5 m左右的位置,同时将全景相机相对于摄站1的方位旋转大约10°左右,摄站3位于摄站2的另一斜前方大约0.5 m处,全景相机继续朝同一旋转方向再次旋转10°左右,以此类推,共采集了10个摄站的60张标定影像,如图 6所示。

|
| 图 6 同步曝光的单摄站6张标定影像 |
根据摄影位置参数,通过影像自动匹配,构建整体平差区域网。同一单相机不同摄站的多基线影像组成一个单航带自由网,6个单相机共有6个单航带,通过相邻相机影像之间的重叠区域将单航带之间联系起来,组成一个大区域网。按照式(9) 对每个同名像点建立误差方程,加入控制点进行整体光束法空三平差,标定结果见表 1。利用此次标定参数进行了柱面全景影像的拼接,效果如图 7所示。可以看出全景影像接边处的拼接误差较小,完全可以满足视觉需求。
| 相机编号 | ΔXSj/m | ΔYSj/m | ΔZSj/m | Δφj/(°) | Δωj/(°) | Δκj/(°) |
| 1号相机 | 0.172 5 | -0.099 1 | 0.008 6 | -116.298 7 | 1.532 2 | 8.088 1 |
| 2号相机 | -0.006 8 | -0.194 0 | 0.041 7 | 179.953 2 | 18.446 2 | 0.162 2 |
| 3号相机 | -0.178 9 | -0.102 0 | 0.011 5 | 114.615 7 | 24.594 3 | 9.367 2 |
| 4号相机 | -0.180 6 | 0.089 2 | -0.019 3 | 60.377 2 | 14.750 4 | 8.023 7 |
| 5号相机 | -0.012 8 | 0.190 4 | -0.022 9 | 0.002 2 | 0.010 5 | 0.036 9 |
| 6号相机 | 0.171 5 | 0.093 3 | -0.025 7 | -64.268 1 | 9.775 1 | 9.047 5 |

|
| 图 7 由标定参数拼接的柱面全景影像 |
本文参考航空摄影测量中空中三角测量的思想,提出了一种采用具有一定重叠度的多个摄影方向的多张标定影像构建整体区域网并加入部分物方控制点后联合进行光束法空三平差进行全景相机的标定方法,该方法可提高标定结果的可靠性和精度,降低对标定场中控制点布设方案的过多依赖。严密标定结果用于全景影像的拼接,拼接效果不仅可以满足视觉上的需求,还可以提供全景影像与单影像之间的坐标映射关系,为全景影像的量测应用提供详细具体的参数,为车载系统多传感器之间的相互标定提供便利。本文提出的全景相机严密标定方法也可为其他组合形式的多拼相机的精确标定提供参考。
| [1] | 石丽梅, 赵红蕊, 李明海, 等. 车载移动测图系统外方位元素标定方法[J]. 测绘学报, 2015, 44(1): 52–58. DOI:10.11947/j.AGCS.2015.20130203 |
| [2] | 闫利, 曹亮, 陈长军, 等. 车载全景影像与激光点云数据配准方法研究[J]. 测绘通报, 2015(3): 32–36. |
| [3] | 季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94–100. |
| [4] | 钟若飞, 孙振兴, 宫辉力. 基于三维激光点云的全景相机标定方法: 中国, 103994779[P]. 2014-05-27. |
| [5] | 李艳红, 李海亭, 庞小平, 等. 采用投影回归原理的全景影像测量方法[J]. 武汉大学学报(信息科学版), 2014, 39(1): 32–36. |
| [6] | ANGUELOV D, DULONG C, FILIP D, et al. Google Street View:Capturing the World at Street Level[J]. Computer, 2010, 43(6): 32–38. DOI:10.1109/MC.2010.170 |
| [7] | 宋杨, 曾凡洋, 李长辉, 等. 基于共线原理的全景影像真彩色点云生成算法[J]. 测绘工程, 2015, 24(4): 1–5. |
| [8] | 季顺平, 史云. 多镜头组合型全景相机两种成像模型的定位精度比较[J]. 测绘学报, 2014, 43(12): 1252–1258. |
| [9] | PARIAN A, GRUEN A. Sensor Modeling, Self-calibration and Accuracy Testing of Panoramic Cameras and Laser Scanners[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65: 60–70. DOI:10.1016/j.isprsjprs.2009.08.005 |
| [10] | 李邓邓. 全景图像拼接算法的研究与实现[D]. 杭州: 浙江工业大学, 2012. http: //cdmd. cnki. com. cn/Article/CDMD-10337-1013146493. htm |
| [11] | SHI Yun, JI Shunping, SHI Zhongchao, et al. GPS-supported Visual SLAM with a Rigorous Sensor Model for a Panoramic Camera in Outdoor Environments[J]. Sensors, 2013, 13(1): 119–136. |
| [12] | JI Shunping, SHI Yun, SHI Zhongchao, et al. Comparison of Two Panoramic Sensor Models for Precise 3D Measurements[J]. Photogrammetric Engineering and Remote Sensing, 2014, 80(3): 229–238. DOI:10.14358/PERS.80.3.229 |
| [13] | IKEDA S, SATO T, YOKOYA N.A Calibration Method for an Omnidirectional Multi-camera Systen[C]//Stereoscopic Displays and Virtual Reality Systems X.Ikoma:[s.n.], 2003. |
| [14] | 王冬. 基于多片空间后方交会的CCD相机检校[D]. 青岛: 山东科技大学, 2003. http: //cdmd. cnki. com. cn/Article/CDMD-10424-2003124300. htm |
| [15] | 张剑清, 胡安文. 多基线摄影测量前方交会方法及精度分析[J]. 武汉大学学报(信息科学版), 2007, 32(10): 847–851. |
| [16] | 柯涛, 张祖勋, 张剑清. 旋转多基线数字近景摄影测量[J]. 武汉大学学报(信息科学版), 2009, 34(1): 44–51. |


