作为一种先进的对地观测技术,干涉合成孔径雷达(InSAR)技术已经成为快速获取三维地形的一种重要工具。1974年,Graham首次提出InSAR地图制图的设想,开创了InSAR对地观测中获取三维信息的先河[1]。Goldstein[2-3]和Lin[4]研究了InSAR技术生成高精度DEM的潜在性。2000年,美国国家航空航天局航天飞机雷达测图任务(SRTM)实现了北纬60°与南纬56°之间大部分陆地面积的测图任务[5]。
在重复轨道模式中,时间去相干影响了DEM的精度,特别是在两次成像期间地表属性不稳定的地区。对于这种情况,可以采用时间间隔比较短的干涉对来削弱时间去相干的误差。2007和2010年,德国分别发射了TerraSAR-X和TanDEM-X卫星组成了双星系统,其时间间隔为几秒,很好地解决了时间去相干的影响[6-8]。众多学者对TanDEM-X InSAR生成DEM开展了研究。K.Dldhuset等采用TanDEM-X数据融合立体SAR和干涉SAR来生成DEM[9];Cristian Rossi等利用TanDEM-X对城市进行DEM的生成和分析[10];Astrid等研究了多方向TanDEM-X DEM的拼接[11]。这些充分显示了TanDEM获取高精度DEM的优势。
相对于C波段的ERS、ASAR和L波段的ALOS,X波段的高分辨率TerraSAR影像干涉条纹更密集,解缠更加困难。针对这一问题,本文设计了一种低分辨率SRTM辅助高分辨率的X波段的TerraSAR干涉相位解缠方案,提高了解缠的效率和精度。为了分析验证TanDEM获取的DEM能否满足测图的要求,需要对生成的DEM进行精度分析。目前,InSAR DEM的精度评价主要采取均方根误差的方法[9-10, 12-15]。该方法通过对InSAR DEM与参考DEM作差得到高程差,然后求取高程差的均方根。也有采用求高程差的均值和方差的方式。在地形起伏很大或相干性较低的地区,TanDEM干涉生成的DEM会存在错误,在某些地形发生了改变的局部地区,InSAR干涉生成的DEM与参考DEM也会存在很大的差异。在这种情况下,采用均方根误差对InSAR生成的DEM进行精度评价会不符合真实情况。针对这一问题,本文研究一种基于协方差函数的方法对TDX/TSX DEM进行精度分析和评价。最后选择一实际区域的TDX/TSX SAR影像数据进行研究,验证方法的可行性。
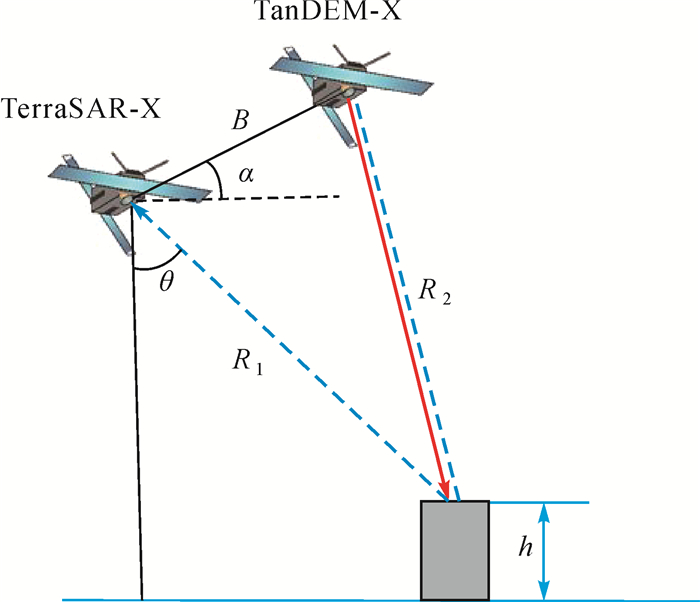
1 方法 1.1 TanDEM-X/TerraSAR-X干涉生成DEM原理TanDEM是德国宇航局为生产高精度DEM提供的高分辨率SAR影像像对,分辨率为3 m,覆盖范围为35 km×50 km。该数据由TerraSAR-X和TanDEM-X两颗成像参数一致的SAR卫星组成双星系统,其成像几何如图 1所示。
|
| 图 1 TanDEM-X/TerraSAR-X成像几何 |
根据图 1的几何关系,两颗卫星收到的脉冲相位信息分别为
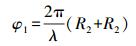 (1)
(1) 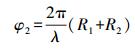 (2)
(2) 式中,R1和R2分别是卫星TerraSAR-X和TanDEM-X到地面的距离;λ为雷达波长。则干涉相位差为
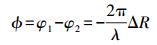 (3)
(3) 式中,ΔR=R1-R2。
由于TanDEM特殊成像几何条件,干涉相位不用考虑大气误差和形变的影响,因此干涉相位由三部分组成
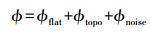 (4)
(4) 式中,ϕflat称为平地相位;ϕtopo为地形相位;ϕnoise为噪音。
通过去平地效应可以去除平地相位ϕflat,通过滤波可以去除噪音ϕnoise,这样即可得到最终的地形相位ϕtopo。
进而利用式(5),可以将地形相位转换为高程,经过地理编码可以得到最终所需要的高精度的DEM
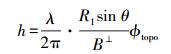 (5)
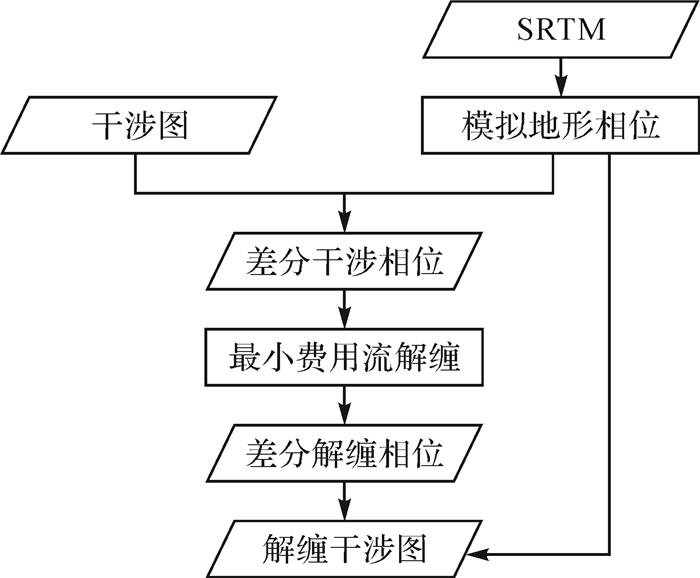
(5) 在式(5) 中,当高差固定不变时,波长越短,相位差变化越大,在未解缠的干涉图中表现为更多的条纹数。相比于C波段的ERS、ASAR及L波段的PALSAR卫星,X波段的TerraSAR的波长更短,因此干涉图的条纹更密集,给解缠带来了困难。在传统的解缠方法中,都有一个假设前提,即相邻像素之间的相位差不超过2π。对于X波段的TerraSAR干涉图来说,相邻像素之间相位差超过2π的可能性越大(尤其是地形起伏较大的地区),导致在一定程度上会降低解缠结果的精度。针对这一问题,本文设计了一种SRTM辅助TerraSAR相位解缠方法,具体流程如图 2所示。
|
| 图 2 SRTM辅助相位解缠流程 |
由于X波段的TerraSAR干涉图条纹比较密集,尤其是在地形起伏较大的区域,常规的3种解缠方法直接对该干涉图进行解缠有两个缺陷:一是因为条纹密集,解缠困难;二是因为该干涉图更容易发生相位的不连续,解缠也容易发生错误。SRTM辅助TerraSAR相位解缠方法通过两步走策略可以解决上面的两个问题。步骤1是基于SRTM的干涉图条纹稀疏化;步骤2是基于最小费用流的干涉图相位解缠。
步骤1的主要目的是从干涉图中去除主要地形对相位的贡献,这样可以减少条纹的密度程度,同时改善干涉图的相位连续性。首先基于TerraSAR轨道参数和距离多普勒SAR构像模型,并结合式(5) 对SRTM进行相位模拟得到TerraSAR坐标系下的SRTM对应的相位。在此基础上,将高分辨率X波段的TerraSAR干涉相位减去模拟的相位,得到低条纹率的干涉图。
步骤2使用最小费用流方法对低条纹率的干涉图进行相位解缠,将得到的解缠结果与SRTM模拟的地形相位相加即可得到最终的解缠结果。
1.3 TanDEM-X/TerraSAR-X DEM精度评价一般用于评价TanDEM-X/TerraSAR-X DEM精度的方法为均方根误差法,该方法是对TanDEM-X DEM每个像素的高程值与其对应外部DEM像素的高程值之间的差异进行估计的。采用均方根误差e对DEM数据进行精度评定,其具体的表达式如下
 (6)
(6) 式中,ZTanDEMi和ZReali分别表示TanDEM-X DEM高程值与外部DEM真实值。用该方法评定精度有两个问题:一是不能考虑各高程差之间的相关性。对于同一像对相干求得的各像素的高程具有很强的相关性,上述计算方法难以体现。二是难以小范围内的高程差异常对InSAR DEM精度评价的影响。即在地形起伏很大、相干性较低的地区或某些地形发生改变的局部地区,高程差在很小的范围内会可能出现较大的变化,直接使用上述方法对InSAR DEM进行的评价结果会产生误差,从而难以客观、真实地反映InSAR DEM的精度。
在地学领域中,经常使用协方差函数来描述空间点位误差及变化[16-17]。根据地统计学中的变异函数理论,斜变差函数可以表示为
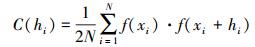 (7)
(7) 式中,hi表示距离间隔;N表示给定距离hi时采样点对的个数;xi表示影像中随机采样点位置;f(xi)表示在影像随机采样点xi上的高差值,表示为
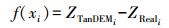 (8)
(8) 在选取的研究区域内,针对每个距离hi,根据式(7) 计算其斜变差函数。然后使用一个非负协方差函数来拟合协方差函数
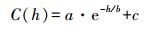 (9)
(9) 在式(7) 中,令hi=0,则C(0) 等价于均方根误差(RMSE)的平方,即式(6) 中e的平方。通过协方差函数法以后,在式(9) 中令h=0,然后对C(0) 开方即可得到TDX/TSX干涉生成的DEM的精度估计值,即
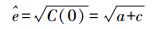 (10)
(10) 在理想情况下,InSAR DEM与参考DEM之间的高程误差都趋于0,是一个比较连续的曲面。但是在地形起伏很大、相干性较低的地区或某些地形发生改变的局部地区,高程误差在很小的范围内会出现较大的变化,采用常规的均方根误差法作为InSAR DEM的评价结果会产生误差。因为式(6) 计算得到的值等价于式(7) 中距离为0的高差值的协方差,也就是说常规的均方根误差法会受到小范围内高程异常的影响。将所有距离的协方差值通过式(10) 借助最小二乘拟合后,然后根据式(10) 再计算距离为0高差值之间的协方差,就可以消除小范围内造成高程差异常的影响,从而得到更符合实际情况的InSAR DEM精度值。
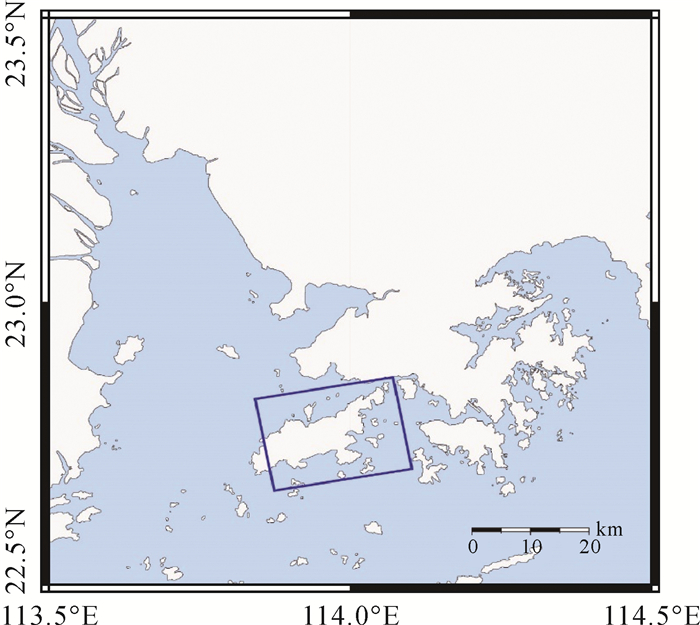
2 试验及分析 2.1 试验数据本文选取研究区域的一对TanDEM-X/TerraSAR-X影像作为试验数据,其影像地理位置如图 3所示。
|
| 图 3 TanDEM-X/TerraSAR-X影像地理位置 |
两幅影像的成像时间为2013年1月1日,成像模式为条带模式。最初获得的影像数据格式并非SLC格式,需要将初始的数据格式转换为单视复数影像数据。
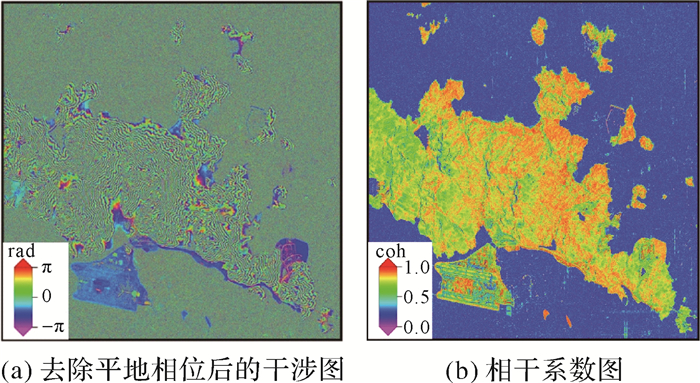
2.2 TanDEM-X/TerraSAR-X干涉生成DEMTanDEM-X/TerraSAR-X干涉生成DEM首先是影像的配准,用来消除同一地区成像的两幅影像之间的位置偏移及旋转。影像配准后,两幅影像经过共轭相乘可得到干涉相位图。生成干涉图后需要去除平地相位的影响。由于地球曲率的影响,即使是在平地上,各点之间也存在着有规律变化的相位差,称为平地相位。因此在分析各点之间由于高差变化引起的相位差时,必须先去除前者,去除平地相位的干涉图如图 4(a)所示。从图 4(a)中可以看见表示地形的清晰的密集的条纹。
|
| 图 4 去平干涉图及相干系数图 |
在处理过程中,也同时得到了研究区域的相干性,如图 4(b)所示。从图 4(b)中可以看到相干值大部分都在0.7以上,这也说明了TanDEM-X/TerraSAR-X干涉生成高精度数DEM有明显的优势。
经过上面处理以后,就得到了仅仅包含地形的相位。因为干涉图中的地形相位值是处于(-π, π]的缠绕值,因此需要将相位由主值恢复到真值,该过程之为相位解缠。由于TanDEM-X/TerraSAR-X采用的波长是更短的X波段,干涉条纹率也大大增加,从而造成了解缠的困难。本文采用C波段的SRTM来辅助高分辨率的X波段TanDEM-X/TerraSAR-X干涉的相位解缠。首先将干涉相位减去SRTM模拟的相位,这样可以使干涉条纹变得稀疏,从而大大减轻相位解缠的难度,并提高解缠结果的可靠性。获得解缠相位后,将该相位加上外部SRTM模拟的相位就是解缠的地形相位。
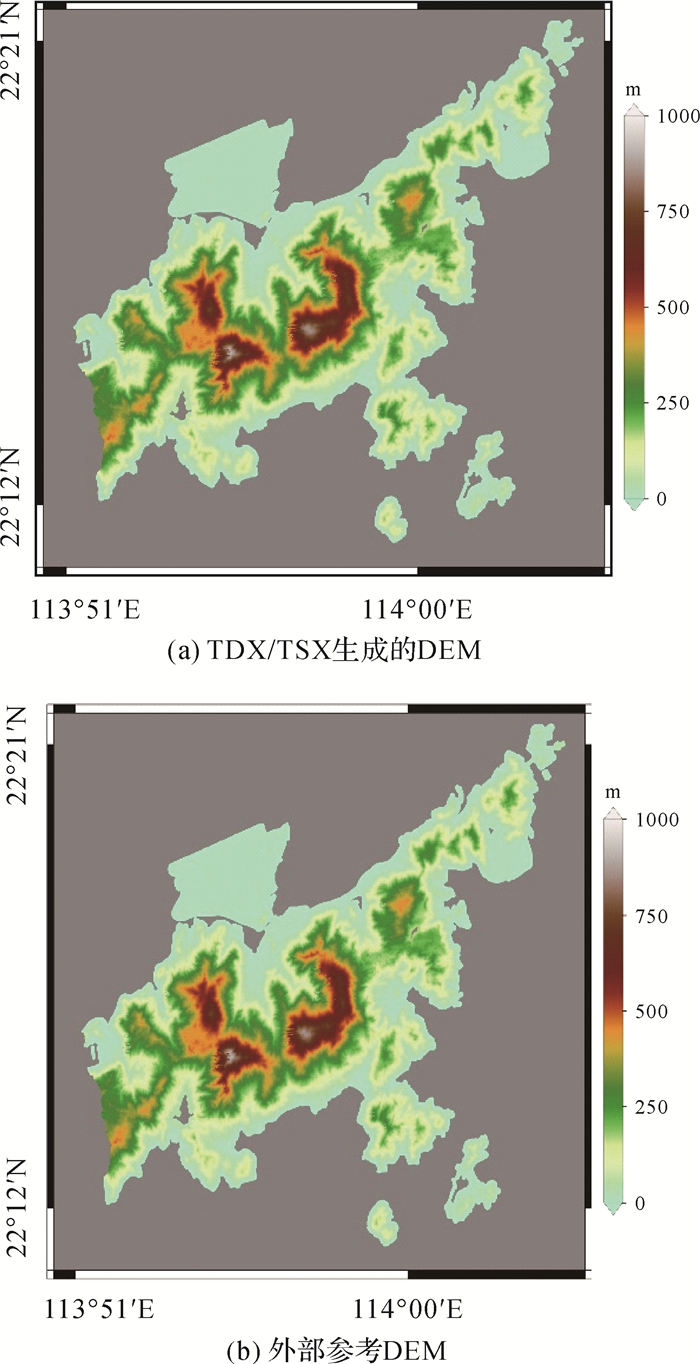
通过相位到高程的计算处理,即可生成SAR坐标系下的高程图,最后将SAR坐标系下的高程图进行地理编码处理,从而获取最终的高精度DEM,如图 5(a)所示。
|
| 图 5 TDX/TSX生成的DEM及外部参考DEM |
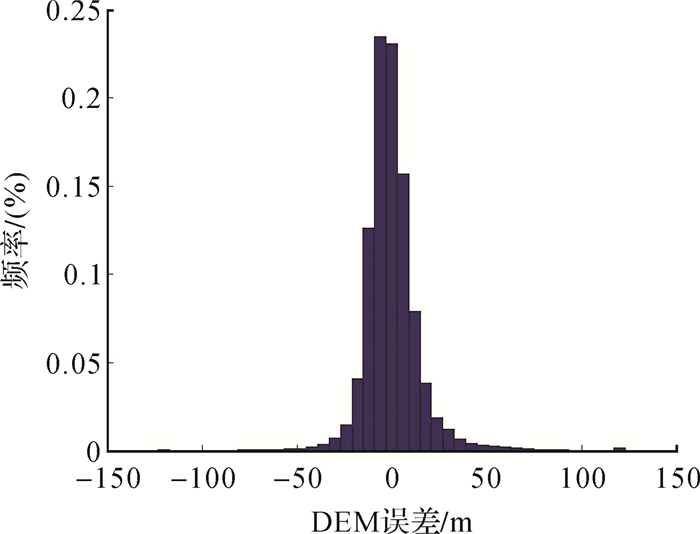
试验采用的外部验证数据为5 m分辨率和1 m高程精度的DEM,如图 5(b)所示。将TanDEM干涉生成的DEM与外部验证DEM作差得到高程误差,然后对高程误差进行统计,结果如图 6所示。
|
| 图 6 TDX/TSX干涉DEM高程误差统计 |
从图 6中可以看出,高程误差的绝对值绝大多数集中在0~4 m之间,占比达到90%以上。
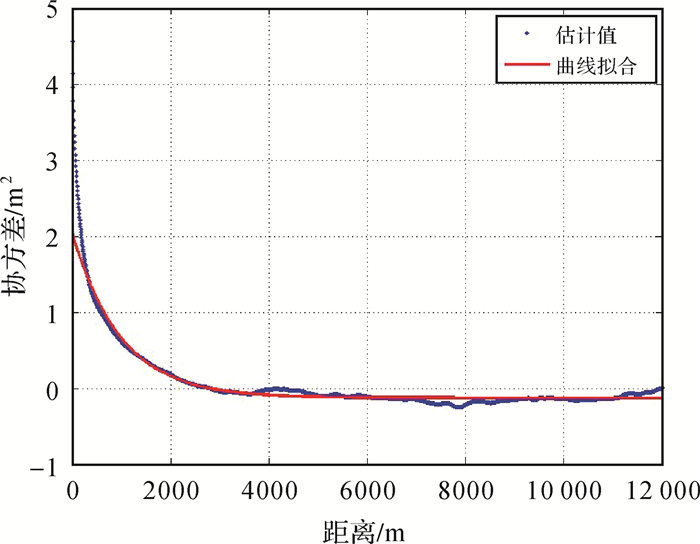
下面采用协方差来对高程误差进行分析。在研究区域内,针对每个距离h利用式(7) 计算其相应的协方差,如图 7所示。这里选取的距离范围为0~12 km。从图 7中可以看到,在距离大于3 km时,协方差估计值趋于稳定;当距离大于6 km时,协方差估计值基本不再变化。从图 7中可以看出,只需要选取最大距离为6 km即可拟合出满足要求的协方差函数。
|
| 图 7 不同距离的协方差估计值及拟合结果 |
接着采用式(9) 来对协方差计算值进行函数拟合,得到协方差函数,如图 7所示,具体表达式如下
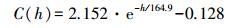 (11)
(11) 在式(11) 中,令h=0,则C(0)=2.024 m2,TDX/TSX干涉获取的DEM的均方根误差估计值为ê=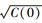
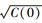
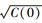
从上面的计算结果来看,拟合后的协方差函数在h=0处的函数值小于均方根误差。因为在地形起伏很大或相干性较低的地区,TanDEM干涉生成的DEM会存在错误。另外,在某些地形发生改变的局部地区,InSAR干涉生成的DEM与参考DEM会存在很大的差异。这些情况造成了小范围内高程误差的异常,也就是说,在较小距离之间的高程误差发生了很大的变化。这也进一步说明了在利用协方差函数法对协方差进行最小二乘拟合后再计算距离为0的协方差值,可以在一定程度上消除小范围内高程误差异常对精度评价的影响,最终得到的精度更客观,更接近真实精度。
3 结语近年来,随着TanDEM-X和TerraSAR-X卫星的发射,生成高精度的DEM已成为可能。本文对试验地区的TanDEM-X/TerraSAR-X影像进行了干涉处理,采用DInSAR的处理手段获取了高精度的DEM。为了验证TanDEM获取的DEM能否满足测图的要求,本文采用协方差函数法对其生成的DEM进行了精度分析。该方法能更真实反映出DEM的精度,结果显示,采用协方差函数方法来评价DEM的精度是可行的。TerraSAR-X/TanDEM-X干涉生成的DEM总体精度达到了1.42 m,这也表明了TanDEM-X在1:10 000测图方面的可行性,能够为我国测图提供有力的技术支撑。
| [1] | GRAHAM L C. Synthesis Interferometric Radar for Topographic Mapping[J]. Proceedings of The IEEE, 1974, 62(6): 763–768. DOI:10.1109/PROC.1974.9516 |
| [2] | ZEBKER H, GOLDSTEIN R M. Topographic Mapping from Interferometric Synthetic Aperture Radar Observations[J]. Journal of Geophysics Research, 1986, 91(B5): 4993–4999. DOI:10.1029/JB091iB05p04993 |
| [3] | GOLDSTEIN R M, ZEBKER H A, WERNER C L. Satellite Radar Interferometry:Two-dimensional Phase Unwrapping[J]. Radio Science, 1988, 23(4): 713–720. DOI:10.1029/RS023i004p00713 |
| [4] | LIN Q, VESECKY J, ZEBKER H. Comparison of Elevation Derived from InSAR Data with DEM over Large Relief Terrain[J]. International Journal of Remote Sensing, 1994, 15(9): 1775–1790. DOI:10.1080/01431169408954208 |
| [5] | MOHR J J, MADSEN S N. Automatic Generation of Large Scale ERS DEMs and Displacement Maps[C]//Fringe'99. Liege, Belgium:[s.n.], 2000. |
| [6] | BREIT H, FRITZ T, BALSS U, et al. TerraSAR-X SAR Processing and Products[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 727–740. DOI:10.1109/TGRS.2009.2035497 |
| [7] | MARTONE M, BRAUTIGAM B, KRIEGER G. Decorrelation Effects in Bistatic TanDEM-X Data[C]//IEEE International Geoscience and Remote Sensing Symposium. Munich:IEEE, 2012. |
| [8] | HAJNSEK I, BUSCHE T. TanDEM-X:Science activities[C]//IEEE International Geoscience and Remote Sensing Symposum (IGARSS).Milan:IEEE, 2015. |
| [9] | ELDHUSET K, WEYDAHL D J. Using Stereo SAR and InSAR by Combining the COSMO-SkyMed and the TanDEM-X Mission Satellites for Estimation of Absolute Height[J]. International Journal of Remote Sensing, 2013, 34(23): 8463–8474. DOI:10.1080/01431161.2013.843808 |
| [10] | ROSSI C, GERNHARDT S. Urban DEM Generation, Analysis and Enhancements Using TanDEM-X[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 85(8): 120–131. |
| [11] | GRUBER A, WESSEL B, MARTONE M, et al. The TanDEM-X DEM Mosaicking:Fusion of Multiple Acquisitions Using InSAR Quality Parameters[J]. IEEE Journal of Selected Topics in Applied Earth Observation and Remote Sensing, 2016, 9(3): 1047–1057. DOI:10.1109/JSTARS.2015.2421879 |
| [12] | SHABOU A, TUPIN F. A Markovian Approach for DEM Estimation from Multiple InSAR Data with Atmospheric Congtributions[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 764–768. DOI:10.1109/LGRS.2011.2181326 |
| [13] | MURA J C, PINHEIRO M, ROSA R, et al. A Phase-Offset Estimation Method for InSAR DEM Generation Based on Phase-Offset Function[J]. Remote Sensing, 2012, 4(3): 745–761. |
| [14] | PERNA S, ESPOSITO C, BERARDINO P, et al. Phase Offset Calculation for Airborne InSAR DEM Generation Without Corner Refectors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2713–2726. DOI:10.1109/TGRS.2014.2363937 |
| [15] | YUAN Z H, DENG Y K, LI F, et al. Multichannel InSAR DEM Reconstruction through Improved Closed-Form Robust Chinese Remainder Theorem[J]. IEEE Geoscience and Remote Sensing, 2013, 10(6): 1314–1318. DOI:10.1109/LGRS.2013.2238886 |
| [16] | ISAAKS E H, SRIVASTAVA R M. Applied Geostatistics[M]. New York: Oxford University Press, 1989: 196-236. |
| [17] | 刘爱利, 王培法, 丁园圆. 地统计学概论[M]. 北京: 科学出版社, 2012: 53-56. |


