2. 中国测绘科学研究院, 北京 100830
2. Chinese Academy of Surveying & Mapping, Beijing 100830, China
地球自转参数(earth rotation parameters,ERP)在空间大地测量、激光测月、深空探测等领域具有很大的影响,因此高精度的地球自转参数预报具有重大意义。地球自转参数包括极移参数、日长变化、UT1-UTC,极移参数又包括X、Y两个方向上的极移分量。地球的公转和自转是周期性变化的,在一定的时间范围内,地球自转参数变化是能够找出一定规律的,若掌握并加以利用这种规律将给予导航定位、航空航天事业及其产业带来无限的裨益。如今国际上常用的地球自转参数预报方法有最小二乘、卡尔曼滤波、神经网络方法、协方差法等,地球自转参数预报精度达到了一定的水平。近几年随着航空航天技术和测量技术的发展,ERP预报的方法得到重大改进,预报精度也有很大的提高。陈略等于2014年提出了地球极移参数高精度双差分LS+AR预报方法[1];许雪晴等提出了AR和卡尔曼滤波组合的地球定向参数高精度预报方法[2];张卫星等研究了EOP预报误差对自主定轨结果的影响[5];姚宜斌等于2013年基于试验提出了一种适用于极移预报的附加误差修正的LS+AR新模型[6];李军等利用LS+AR模型和激发函数方法预报了地球自转参数[8];杨杰等于2013年进行了基于ARIMA模型的地球自转参数预报研究[9];2014年叶修松等于2014年采用长自回归白噪化方法对地球自转参数进行了短期预报[10]。本文利用LS+AR方法对ERP进行进一步研究和预报,以发现ERP新的预报规律。
1 LS+AR模型一般情况下,极移信号中存在半年项、周年项和钱德勒项等信号,因此可将极移信号设定为
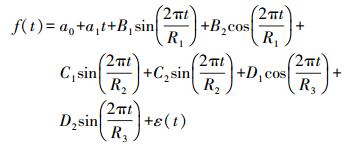 (1)
(1) 式中,a0为常数项;a1为趋势项的拟合系数;B1、B2表示极移序列模型中半年摆动项参数; C1、C2表示极移序列模型中周年摆动项参数; D1、D2表示极移序列模型中钱德勒摆动项参数。
长期预报所用的时间序列长度包含了半年项、周期项、钱德勒项等,而在短期预报中数据序列长度较短不足以显示出半年项、周期项、钱德勒项,因此式(1) 就简化为
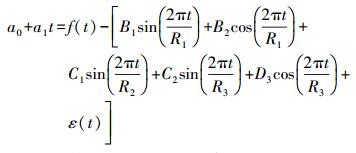 (2)
(2) AR模型表示平稳随机序列xt(t=1, 2, …, n)在t时刻以前的规律性变化和t时刻白噪声的关系,其数学模型为
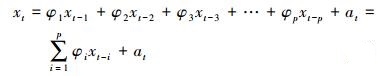 (3)
(3) 式中,φ1、φ2、…、φp为模型参数; at为白噪声; p为模型阶数; at~N(0,σ),σ为白噪声的方差。式(3) 称为p阶自回归模型,简记为AR(p)。
运用AR模型的关键在于确定合适的模型阶数p。常用的模型定阶方法有最终预测误差(FPE)准则、信息论(AIC)准则及传递函数(BIC)准则。本文采用FPE准则来确定,FPE准则依据模型预报误差来确定自回归模型的最佳阶数,即使得模型的最终预报误差最小。关于AR(p),FPE函数定义如下
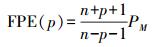 (4)
(4) 式中
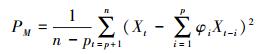 (5)
(5) 使FPE(p)达到最小值的p就确定为AR模型的阶数。
在建立自回归模型时,关于AR模型阶数的确定可以利用Matlab工具箱中的函数来解决。确定阶数后,即可用最小二乘方法估计出模型参数。
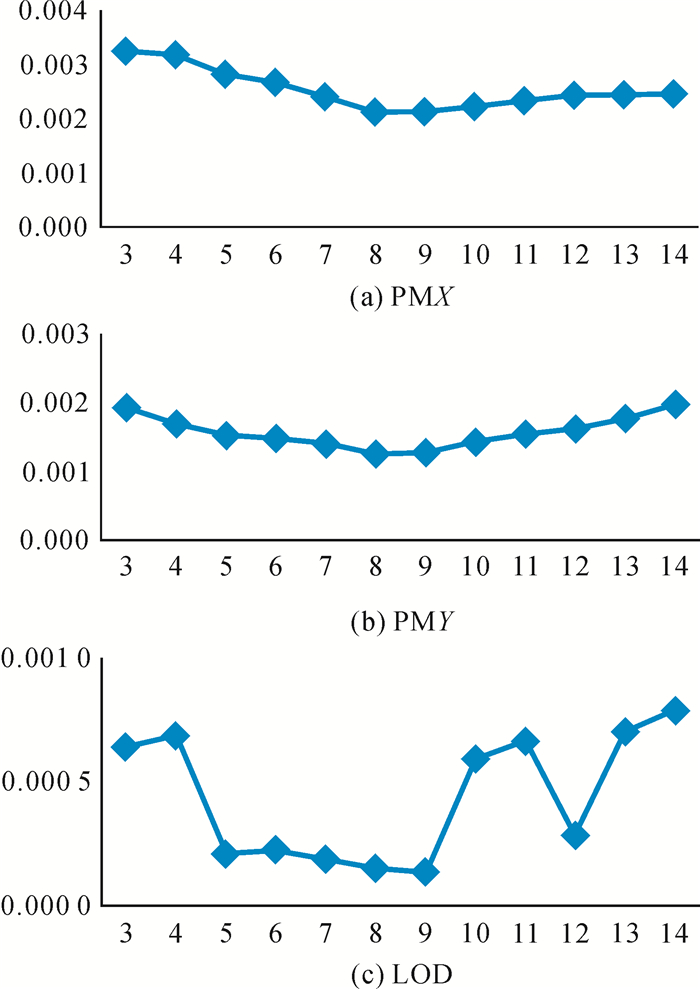
2 数据处理及精度对比分析本文的试验数据皆来自北斗分析中心(CGS),试验方法是利用最小二乘法和自回归模型算法自主编程处理,将试验结果与IGS预报结果进行作差对比。首先用最小二乘单独进行试验,探究出预报的最佳数据。试验结果如图 1所示。
|
| 图 1 |
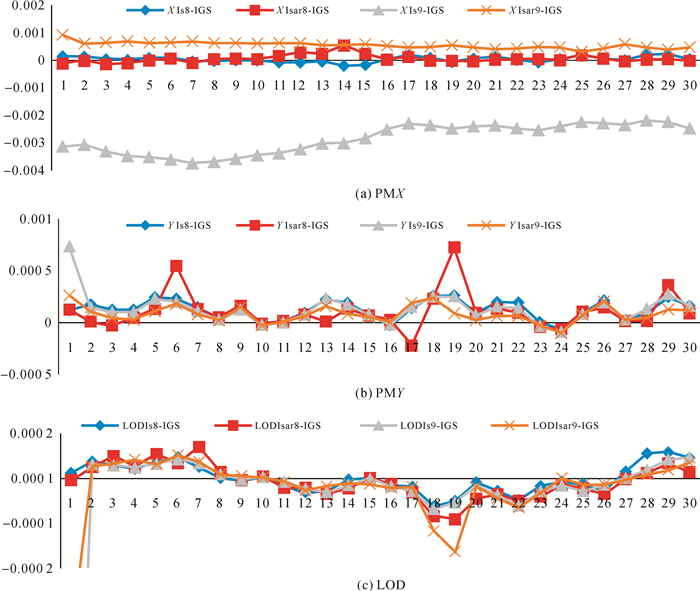
从图中可以看出,试验中8个时段与9个时段处理的结果精度相对较高。以下的对比试验中用8个时段与9个时段数据长度单独进行试验分析。试验结果对比如图 2所示。
|
| 图 2 |
从图中可以看出,用LS+AR联合进行预报的精度高于LS单独预报,且在进行PMX预报时利用8个时段数据和9个时段数据的预报精度对比之后发现,利用8个时段数据的预报精度较高,而进行PMY预报时利用9个时段数据的预报精度较高,进行LOD预报时在进行极移预报时利用8个时段精度较高。
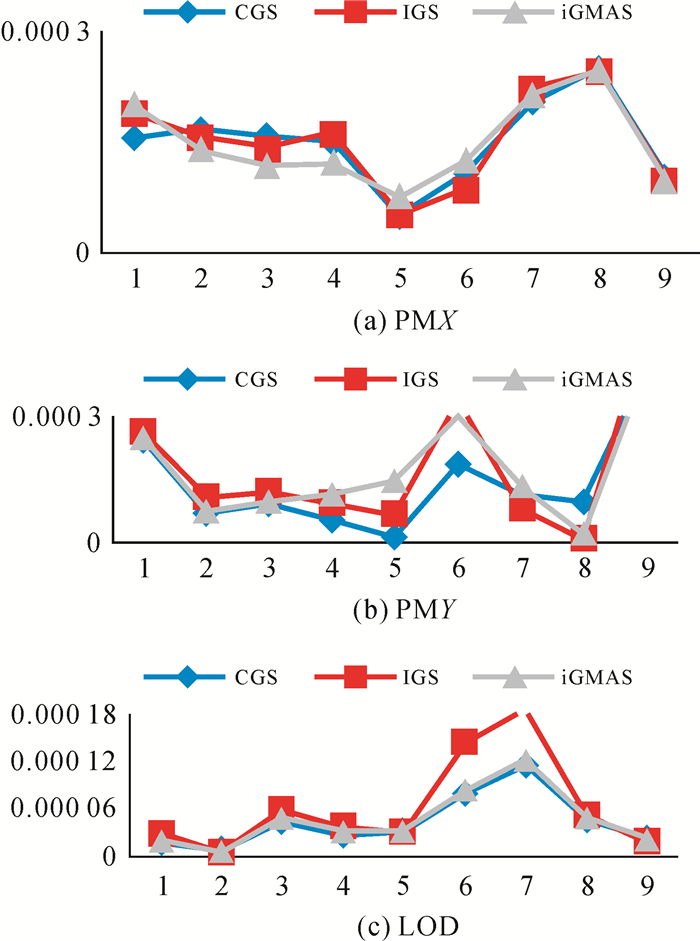
将预报结果和国际国内知名预报单位的预报结果进行对比分析,部分结果如图 3所示。
|
| 图 3 |
从图中趋势上可以看出,X、Y两个方向上的极移和日长变化的预报上的结果与IGS、iGMAS的预报结果有很强的一致性。这样就引出了以时段为单位预报和以天为单位预报的精度应有所不同的猜想,以及猜想的试验验证,用连续的U00/U06/U12/U18的数据进行预报,然后与以天为单位的数据试验进行对比,将以天为单位的数据预报与以时段为单位的数据预报的试验结果加入分析中心当前线性预报,作对比,如图 4所示。
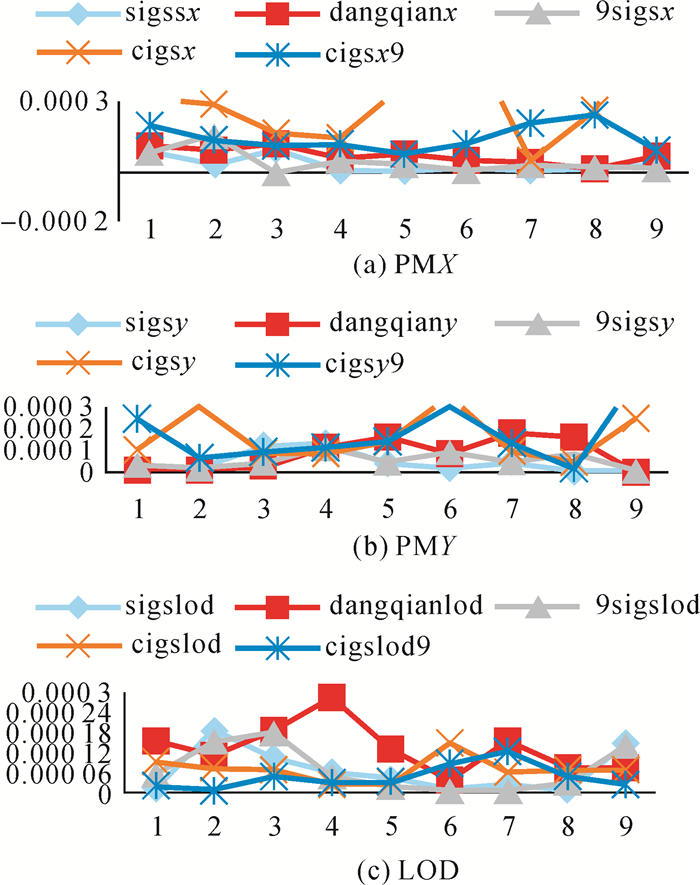
|
| 图 4 |
从图中可以看出,以时段为单位预报和以天为单位预报时,PMX和PMY的以连续时段为预报单位时预报精度较以天为单位数据预报精度高,但在日长变化的预报中以天为单位数据预报结果精度更高;同时从图中可以得出,极移预报使用的数据以天为单位预报时不如线性的精度高,当以时段为单位预报时LS+AR方法精度要高于线性预报模型,而在LOD预报时线性模型不如LS+AR模型的精度高。在利用高频数据进行预报时极移预报的精度有了很大的提升,日长变化的预报在利用高频数据进行预报时精度反而有一定的降低且不够稳定。
3 结论(1) 从预报模型的选择上来说,LS+AR组合模型的预报精度最高,分析中心的线性模型预报的精度介于LS模型单独预报和LS+AR组合模型预报之间。因此,在进行ERP预报时应当选择合适模型。
(2) 在数据长度适用方面,极移预报中利用8个时段的数据进行预报能得出更高精度的结果,进行日长变化的预报时利用8个时段的数据长度预报的结果精度稍好,因此参数预报类型不同所选择的最佳数据长度应有所区别。
(3) 在使用数据类型方面,在极移预报时用连续的U00/U06/U12/U18的数据进行预报和以天为单位的数据试验进行对比可以明显得出,使用连续的时段数据预报极移能得出精度更高的预报结果,在日长变化的预报中,用连续的U00/U06/U12/U18的数据预报和以天为单位的数据进行预报时,以天为单位的数据进行预报精度更高更稳定,这说明在不同产品的预报中应根据预报产品选择对应的数据类型选择。
| [1] | 陈略, 唐歌实, 许雪晴. 地球极移参数高精度双差分LS+AR预报方法研究[J]. 大地测量与地球动力学, 2015, 35(5): 844–848. |
| [2] | 许雪晴. 地球定向参数高精度预报方法研究[D]. 北京: 中国科学院大学, 2012. http: //cpfd. cnki. com. cn/Article/CPFDTOTAL-WXDH201005002006. htm |
| [3] | 严凤, 姚宜斌. 地球自转参数短期预报方法及实现[J]. 大地测量与地球动力学, 2012, 32(4): 71–75. |
| [4] | 徐爱功, 赵亮, 周阳. 基于PANDA软件的GPS静态精密单点定位精度分析[J]. 测绘通报, 2013(10): 5–7. |
| [5] | 张卫星, 刘万科, 龚晓颖. EOP预报误差对自主定轨结果影响分析[J]. 大地测量与地球动力学, 2011, 31(5): 106–110. |
| [6] | 姚宜斌, 岳顺强, 陈鹏. 一种适用于极移预报的附加误差修正的LS+AR新模型[J]. 中国科学(地球科学), 2013(4): 665–676. |
| [7] | 徐君毅. 地球定向参数预报理论与方法研究[D]. 郑州: 信息工程大学, 2010. http: //cdmd. cnki. com. cn/Article/CDMD-90008-1011056793. htm |
| [8] | 李军, 赵德军, 陈永祥. 利用LS+AR模型和激发函数预报地球自转参数[J]. 大地测量与地球动力学, 2015, 35(3): 57–459. |
| [9] | 杨杰, 叶修松, 曾光, 等. 基于ARIMA模型的地球自转参数预报研究[J]. 导航定位学报, 2016, 4(1): 68–74. |
| [10] | 叶修松, 何雨帆, 曾光, 等. 采用自回归平均模型的地球自转参数短期预报[J]. 导航定位学报, 2014, 2(3): 52–60. |
| [11] | 党亚民, 秘金钟, 成英燕. 全球导航卫星系统原理与应用[M]. 北京: 测绘出版社, 2007. |
| [12] | 王小辉, 王琪洁, 刘建. 经验模式分解在极移超短期预报中的应用[J]. 天文学报, 2012, 53(3): 519–526. |


