2. 中国矿业大学地球科学与测绘工程学院, 北京 100083
2. College of Geoscience and Surveying Engineering, China University of Mining and Technology, Beijing 100083, China
浅地层剖面探测是一种基于水声学原理的连续走航式探测水下浅部地层结构和构造的地球物理方法[1-2]。浅地层剖面仪是对海洋、江河、湖泊底部地层进行剖面显示的设备,结合地质解译,可以探测到水底以下地质构造情况。本文数据采集工作所用仪器为德国Innomar公司生产的SES-2000型参量阵浅地层剖面仪,该仪器有较高的地层分辨率和地层穿透能力,并可以根据数据采集显示界面的实时显示效果选择不同发射频率,现场实时地设计调整工作参量,可以在航道勘测中测量河(海)底的淤泥层厚度,也可以测量在海上油田钻井中的基岩深度和厚度[1-3],因而是一种在海洋地质调查,地球物理勘探和海洋工程,海洋观测、海底资源勘探开发,航道港湾工程,海底管线铺设中广泛应用的仪器。与传统海底探测方法相比,浅剖仪探测浅地层剖面具有成本低、效率高、电子自动成图等优点。但是由于受噪声、多次波等因素的影响,对浅剖图像判读之后的底质层界划分结果往往不尽如人意,近年来,国内不少专家学者针对浅剖数据的这些影响因素进行了分析与研究,王鹏伟等提出了应用变周期预测反褶积压制多次波的方法,试验表明该方法对多次波压制效果明显[4];李淑阔等利用淤泥层反射图像识别技术对淤泥层空间分布与水下淤积进行测定,也得到了较好的结果[5];刘玉萍等利用浅剖资料海底振幅的特征属性直接进行底质分析,通过试验验证了其可行性[6]。本文在消除浅剖图像中噪声、多次波等因素的基础上,依据浅剖原始数据,采用信号分析方法并结合试验区域少量钻孔资料,实现了淤泥层层界的准确划分。
1 浅剖图像处理浅地层剖面数据采集过程中受噪声、气泡、紊流等海洋环境的影响,导致浅剖图像出现模糊、失真及多次波等问题,为后期图像判读和地层提取工作带来困难。通常在判读图像之前都要对浅剖图像数据进行消噪,压制二次波的处理。
1.1 消除噪声受有源噪声和环境噪声影响,浅剖换能器接收的声波信号中会出现大量的噪声信号,实际工作中应滤除。有源噪声是声源或次生源形成的干扰,环境噪声主要是船舶发动机噪声,二者均可采用中值滤波法进行消除。中值滤波属于非线性滤波方法[7-9],是一种基于排序统计理论能有效抑制噪声的平滑滤波信号处理技术。
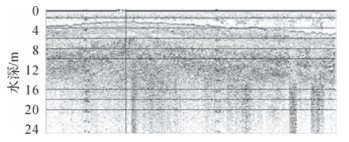
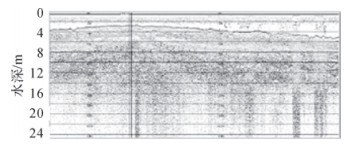
对浅剖原始图像数据进行中值滤波消噪的过程为:首先确定一个以某个像素为中心点的窗口,一般为方形,然后将窗口中各像素的灰度值排序,取排序后的灰度值的中间值作为窗口中心点像素的灰度值,当窗口移动时,利用中值滤波可以对图像进行平滑处理。中值滤波模板的大小决定着滤波的质量,如果模板过小,滤波不明显,如果滤波模板过大,图像会丢失有效信息,这需要结合实际进行试验来选取最合适的滤波模板。图 1与图 2分别为加盐噪声浅剖原始灰度图像和进行中值滤波后的图像,可以看出进行滤波后的噪声得到了明显压制。
|
| 图 1 加盐噪声浅剖灰度图像 |
|
| 图 2 3×3模板中值滤波图像 |
换能器发射的声波波束从海底反射到海面时,因海面与空气的分界面(自由界面)是一个波阻抗差别很明显的界面,其反射系数可以认为是-1,因此是一个良好的反射界面,反射波又可能从这个反射界面向下传播;当遇到反射界面时,又可以再次发生反射返回海面被换能器所接收,这样在浅剖图像上就出现了多次波。
多次波是影响地层层界划分的主要因素,判读浅剖图像前需对其进行压制[10-11]。与地震波相比,浅剖图像中出现的多次波多为规则干扰波,文献[12—14]表明在众多压制多次波的方法中,预测反褶积法压制该类多次波效果最为明显。
设换能器发射的声波b(t)满足最小相位条件,反射系数为白噪声,褶积模型为
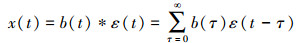 (1)
(1) 式中:x(t)为t时刻反射波强度值;ε(t)为反射系数;*为褶积运算符。
则t+l时刻输出的反射波强度值为(包含一次波和多次波)
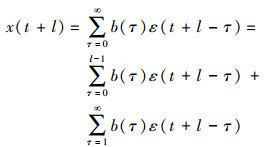 (2)
(2) 与误差公式相对照
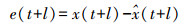 (3)
(3) 式中, e(t+l)为t+l时刻一次波能量值(预测误差);(t+l)为t+l时刻与x(t+l)对应的预测值。
从式(2) 和式(3) 得出
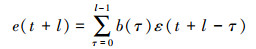 (4)
(4)  (5)
(5) 设b′(t)= b(0), b(1), …,b(τ),则
 (6)
(6) 即将前一个子波的前部与反射系数的褶积就得到了一次反射波。反之,用这种方法可压缩子波长度,提高浅剖图像的分辨率。
由于预测反褶积后,子波被切成l长,因此预测反褶积实际上是一种子波波形1切除反褶积。特别当l=1时,子波变成了δ脉冲,以上预测反褶积实际上变成了脉冲反褶积。
设预测因子c(t)= c(0), c(1), …,c(m)使得
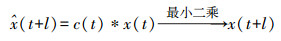 (7)
(7) 根据解经典维纳滤波问题的方法[15],依据最小二乘原则求得预测因子c(t),从而预测出多次波,结合式(3) 即可去除浅剖原始图像中多次波的影响。
2 层界提取浅地层剖面仪按照一定的时间间隔向海底发射声波,由于海水及海底沉积物对声波会有不同程度的吸收,因此声波向海底传播过程中会出现能量的衰减,同时在声阻抗较大的界面也会发生反射。声波在海底处反射的能量取决于反射界面的反射系数,可用瑞利反射系数公式表示为
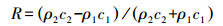 (8)
(8) 式中,ρ1、c1、ρ2、c2分别表示两个层界中介质的密度和声速。
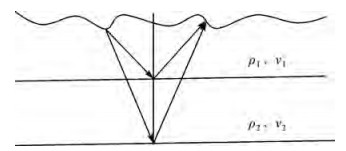
当两个层界中的介质密度与声波传播速度的乘积有较大差值时反射系数将会变大,从而使两不同层界之间的层界面产生相对大的声强,在浅剖图像中会以明显的灰度界面线表现出来,判读浅剖图像时可依据此灰度界面线进行淤泥层层界划分。
|
| 图 3 声波在层间的传播路径 |
从浅剖原始数据中提取出单道剖面数据声强文件,以此表示出声波在一个剖面上不同介质中的振幅大小。声波的振幅与反射能量成正比,可以把一个剖面上不同深度位置的样本反射的声强表现为振幅图像,根据图像中声强的变化趋势分析样本差异性,在信号处理软件选中振幅接近的两个层界面点,利用式(9) 可计算出相似样本的层厚度,达到层界提取目的。
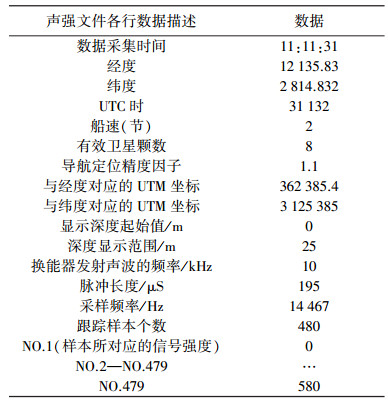
如图 4中M022竖线是浅剖进行数据采集过程中经过钻孔位置时打下的标记,便于后期淤泥层界提取与钻孔资料作对比。图 5是从浅剖原始数据中提取出的在标记M022处的单道信号强度文件,由于单道剖面上跟踪样本数多达480个,因此图 5只是展现了声强数据的一部分,具体说明详见表 1。某一样本的声强对应的深度数据可以按照式(9) 自行计算

|
| 图 4 带有标记M022的原始图像 |

|
| 图 5 与标记M022对应的信号文件 |
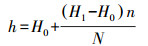 (9)
(9) 式中, h为某一样本对应的深度;H0为深度起始值;H1为深度变化范围值;n为第n个样本;N为该声强文件中总的样本数。
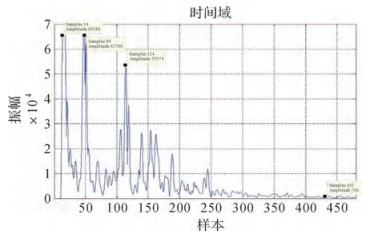
图 6中有3个明显的波峰,结合图 4带有M022标记的经消噪、多次波压制的浅剖灰度图像,可判断样本14、样本48、样本114分别为图中标注的位置,水底位置及层间夹杂有坚硬物质的位置,按照式(9) 可分别求得3个样本位置的深度值分别为0.73 m、2.50 m、5.94 m,则两者之间的差值分别为1.77和3.44 m, 与图 4中样本所处位置的深度值基本符合。
|
| 图 6 标记M022振幅图像 |
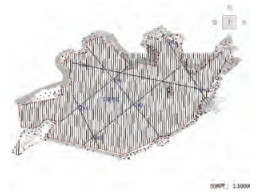
为验证本文方法所划分层界的准确性,在浙江温岭某港池进行了数据采集,并钻孔获取工程地质剖面数据等钻孔资料(ZK1,ZK2,…, ZK7),钻孔位置及测线图如图 7所示,图中高亮圆点的分布为钻孔位置分布。数据采集所用仪器为德国Innomar公司产的SES-2000型参量阵浅地层剖面仪,仪器声波发射频率为10 kHz, 增益水平为18 dB,换能器吃水深度65 cm,数据采集软件中显示深度范围25 m,测量船速度为2~4节,由声速仪测得海水中声速为1507 m/s,并在浅剖数据采集软件中进行声速参数设置。
|
| 图 7 测线与钻孔位置分布 |
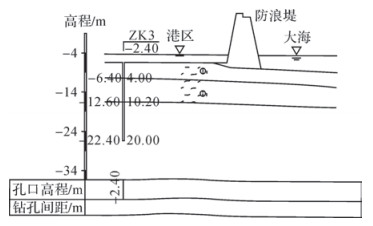
以钻孔3为例,图 4中标记M022即为钻孔3的坐标位置,相应的图 5与图 6分别为该剖面上的声强数据与振幅图像,文章第二部分已确定图 6中样本49为海水与海底沉积物的界面点。考虑到声波能量的衰减及振幅变化趋势,选定样本431为淤泥层与下一层界的界面点,根据式(9) 计算得到两界面点处的深度值分别为2.55和22.45 m, 可得两界面间的层间厚度为19.90 m,与钻孔3的工程地质剖面图 8所示的20.00 m层厚比较,层间厚度相差0.1 m。
|
| 图 8 钻孔3工程地质剖面 |
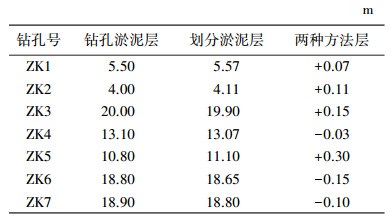
对以上方法提取的层界厚度进行结果分析,结合测区的7个钻孔ZK1、ZK2、…、ZK7提供的层界信息及对应深度信息,分析以上层界划分的准确性。比较二者淤泥层厚度及其层间厚度偏差,结果见表 2。
从表 2可看出,基于本文方法提取的淤泥层层间厚度与钻孔数据提供的淤泥层层间厚度最大偏差为+0.30 m,最小偏差为-0.03 m, 平均偏差为+0.05 m。本文方法提取的层间厚度达到了分米级,与钻孔提供的分米级淤泥层厚度值一致。
4 结论(1) 在浅剖数据预处理过程中,采用中值滤波法对浅剖图像数据进行了消噪处理,使得浅剖原始图像的灰度图像更清晰,同时利用预测反褶积算法进行了多次波压制,使得原始数据可靠性更高。
(2) 提取单道剖面数据的声强文件,借助信号分析技术形成样本-振幅关系图像,选取样本-振幅图像中跳变样本点进行深度计算进而确定出淤泥层层厚,与钻孔资料相较差异性较小,证明基于浅剖数据的淤泥层层界提取方法可行。
(3) 从理论上讲,本文淤泥层层界提取方法在其他海底沉积物层界提取中应同样适用,但是其可靠性有待今后验证。
致谢: 衷心感谢无锡智海科技有限公司李太春总经理和廖荣发工程师在浅剖数据采集工作方面提供的帮助。| [1] | 祝鸿浩. 参量阵浅地层剖面技术研究[D]. 北京: 中国舰船研究院, 2015. |
| [2] | 李平, 杜军. 浅地层剖面探测综述[J]. 海洋通报, 2011, 30(3): 344–350. |
| [3] | 王方旗. 浅地层剖面仪的应用及资料解译研究[D]. 青岛: 国家海洋局第一海洋研究所, 2010. |
| [4] | 薛长虎, 聂桂根, 汪晶. 扩展卡尔曼滤波与粒子滤波性能对比[J]. 测绘通报, 2016(4): 10–14. |
| [5] | 李淑阔. 淤泥层空间分布与水下淤积测定[D]. 济南: 山东大学, 2013. |
| [6] | 刘玉萍, 丁龙翔, 杨志成, 等. 利用浅剖资料进行海底底质分析[J]. 物探与化探, 2016, 40(1): 66–72. |
| [7] | 耿帅. 基于数学形态的图像去噪[D]. 济南: 山东师范大学, 2012. |
| [8] | 赵文胜, 蒋弥, 何秀凤. 干涉图像第二类统计Goldstein自适应滤波方法[J]. 测绘学报, 2016, 45(10): 1200–1209. DOI:10.11947/j.AGCS.2016.20150457 |
| [9] | 赵铁虎. 海底高分辨率声学探测及其应用[D]. 青岛: 中国海洋大学, 2011. |
| [10] | 李列, 谢玉洪, 李志娜, 等. 海上多次波压制与成像方法研究进展[J]. 地球物理学进展, 2015, 30(1): 446–453. DOI:10.6038/pg20150166 |
| [11] | 赵建虎, 冯杰, 施凤, 等. 基于图像处理技术的浅地层层界划分方法[J]. 中国矿业大学学报, 2016, 45(2): 411–417. |
| [12] | 雍凡, 罗水余, 李颜贵, 等. F-K变换与预测反褶积压制多次波效果对比[J]. 物探化探计算技术, 2014, 36(6): 700–707. |
| [13] | 王彦江. 多次波压制方法及应用研究[D]. 北京: 中国地质科学院, 2009. |
| [14] | 刘建辉. 基于波动理论压制多次波方法研究[D]. 北京: 中国石油大学, 2010. |
| [15] | 张军华, 缪彦舒, 郑旭刚, 等. 预测反褶积去多次波几个理论问题探讨[J]. 物探化探计算技术, 2009, 31(1): 6–10. |