2. 深圳大学空间信息智能感知与服务深圳市重点实验室, 广东 深圳 518060;
3. 海军海洋测绘研究所, 天津 300061;
4. 武汉大学地理国情监测国家测绘地理信息局重点实验室, 湖北 武汉 430079
2. Shenzhen Key Laboratory of Spatial Smart Sensing and Services, Shenzhen University, Shenzhen 518060, China;
3. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China;
4. Key Laboratory for National Geographic Census and Monitoring, National Administration of Surveying, Mapping and Geoinformation, Wuhan University, Wuhan 430079, China
目前,在高精度海道测量中,验潮站提供潮位观测值通常受有限距离的限定,验潮站的有效范围取决于深度测量的精度、验潮站与深度点上瞬时(同一时间)的最大潮高差[2]。本文利用FVCOM模式模拟计算得到模拟海域整个场的天文潮潮位值。然后根据模拟区域内分布的长短期验潮站资料提取水位修正模型,将修正水位利用反距离加权算法配置到模拟计算的网格中,得到整个网格每个格点的潮位时间序列,对于区域内的任意点的潮位都可以通过插值得到高精度的潮位。
1 FVCOM水动力模型 1.1 模型方程模型控制方程包括连续性方程、动量方程、温盐扩散方程和密度方程。σ坐标下的控制方程如下
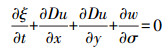 (1)
(1) 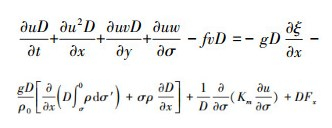 (2)
(2)  (3)
(3) 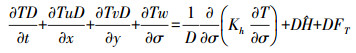 (4)
(4) 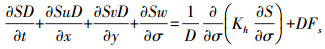 (5)
(5) 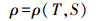 (6)
(6) 式中,t为时间;D为总水深;ξ为水位;u、v、w分别为σ坐标下x、y和σ方向的速度分量,σ取值从海底处的-1到海表面处的0;g为重力加速度;ρ为海水密度;ρ0为水体参考密度;f为科氏参数;Fx、Fy、FT分别为水平向动量、温度和盐度扩散项;T为海水温度;S为海水盐度;
海表面和底部速度边界条件为
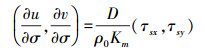 (7)
(7) 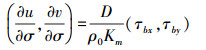 (8)
(8) 式中,(τsx, τsy)和(τbx, τby)分别为海表面风切应力和海底摩擦切应力在x和y方向上的分量。
海表面和底部温盐边界条件为
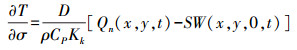 (9)
(9) 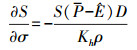 (10)
(10) 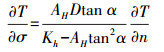 (11)
(11)  (12)
(12) 式中,Qn(x, y, t)为表面净热通量,包括短波辐射、长波辐射、感热和潜热通量4部分;SW(x, y, 0, t)为海表面处短波辐射通量;cp为海水比热系数;
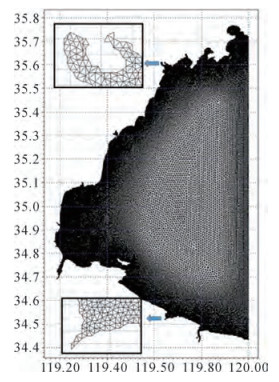
研究区域位于南黄海,包括海州湾及其附近海域,整体范围为119°42′—120°,35°78′—34°41′,水深数据采用电子海图数据,调和常数选用潮汐数据反演模式OTIS。计算网格对岸边和岛屿的网格进行了局部加密,开边界平均分辨率约0.01°,岸线及岛屿附近平均分辨率约0.002°,共包含49 333个网格节点、96 252个水平网格单元。开边界水位采用M2、S2、N2、K2、K1、O1、P1和Q1 8个分潮调和常数给出的预报水位。模式模拟了2007年1月16至2007年2月15日期间海州湾及其外海海域内的潮汐、潮流运动状况,计算过程中每小时输出一次结果。如图 1所示。
|
| 图 1 区域不规则三角网结构 |
本文采用了日照、岚山头、连云港、开山岛和车牛山岛5个验潮站的资料,其中日照和连云港为长期验潮站,岚山头、开山岛和车牛山岛为短期验潮站,短期验潮站进行了一个月的连续验潮。
2.2 水位修正模型设计本文设计的水位修正模型主要包括短周期分潮的水位修正、长周期分潮的水位修正和余水位修正。
2.2.1 长周期分潮水位修正模型长周期分潮必须利用6个月以上的潮位资料才能调和分析出长周期分潮。对日照、连云港两个长期站一年水位资料进行调和分析,得到了Sa、SSa两个主要的长期分潮调和常数,然后对长周期分潮调和常数进行水位预报,从而获取两个长期验潮站的长周期分潮引起的水位起伏时间序列,截取2007年1月27日7时至2007年2月14日16时的水位序列作为长周期分潮水位订正。
2.2.2 短周期分潮及余水位修正模型本文研究区域分布2个长期验潮站和3个短期验潮站,截取5个验潮站2007年1月16日0时至2007年2月15日23时的水位资料进行调和分析,得到了32个常数调和常数。在32个常数中选取了M2、S2、N2、K2、K1、O1、P1和Q1 8个主要分潮的调和常数进行了水位预报。修正水位算法是利用实测水位减去8个分潮的预报水位的方法得到,利用该算法提取了5个验潮站的修正水位时间序列,其数学表达式为
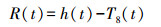 (13)
(13) 式中,h(t)为实测水位;T8(t)为8个分潮的预报水位;R(t)为修正水位,修正水位包括了剩余短周期天文潮和余水位。
2.3 修正水位配置算法通过修正水位算法得到了两组水位修正模型,利用反距离加权算法将两组修正模型的修正水位值插入网格的格点水位值中。在确定的空间尺度L和时间尺度T范围内,单个网格点的水位值的数学表达式为
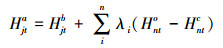 (14)
(14)  (15)
(15) 式中,Hjta为水位H在网格点j处t时刻所求得的水位值;i表示网格点的空间位置;t表示不同的时刻;n表示验潮站点数;Hjtb为水位H在网格点j处t时刻数值模拟的水位值;Hnto为水位H在验潮站n处t时刻的实测潮位值;Hntc为水位H在验潮站n处t时刻的预报水位值;p表示指数值。
3 修正模型验证选用了车牛山岛站、连云港站2个具有代表性的验潮站作为实测资料进行对比试验。其中,车牛山岛验潮站为岛礁短期验潮站,距陆地43 km;连云港站为岸基长期验潮站。提取验潮站站点位置的模拟潮位资料,潮高基准采用理论深度基准面,将模拟潮位资料和验潮站潮位资料的水位和调和常数分别作对比。
3.1 潮位验证图 2和图 3分别为截取两个验潮站部分模拟水位和实测水位的对比,时间为2007年1月20日0时到2007年2月5日23时。可以清楚看到模拟结果和实测结果吻合较好,水位误差不超过50 cm,相位基本一致,模拟的高潮和低潮的发生时间与实测的基本一致。

|
| 图 2 车牛山站模拟水位与实测水位对比 |
|
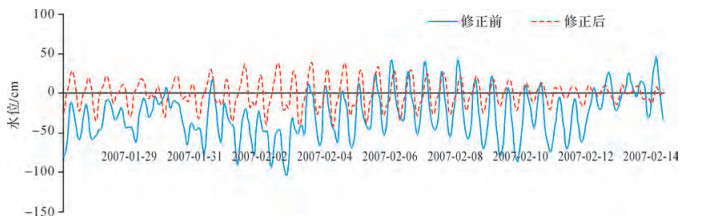
| 图 3 连云港站模拟水位与实测水位对比 |
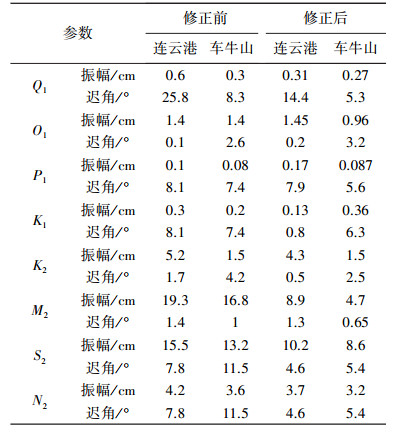
模型计算与验潮站实测调和常数的差值比较见表 1。
对于修正后的水位数据精度评估,采用测量数据处理理论中的中误差指标表示,即
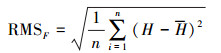 (16)
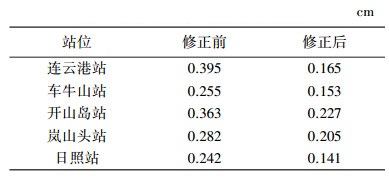
(16) 式中,RMSF表示修正后的水位数据的中误差;H表示修正前后的水位值;H表示验潮站潮位值。比较水位修正前后两个站位的中误差值,结果见表 2。
通过图 1和图 2、图 3比较可以看出,经过水位修正后的潮位相对于模拟结果得到了明显改进,与实测结果吻合度提高,水位误差精度提高了10 cm左右,相位和实测结果也无差别。从表 2中的中误差对比也可以看出,模拟结果的修正前后,潮位得到了明显改善。潮位剩余误差主要来自于两方面:一方面主要来自数值模拟精度不够;另一方面验潮站分布和数量还比较少,使得改正水位模型的精度还不够完善。
4 结语本文利用了FVCOM对海州湾及其外海进行了潮汐数值模拟,利用区域内验潮站资料对数值进行了模拟,得到了各个网格点的潮位,并进行了水位修正,使得修正后的潮位精度相对于数值模拟结果有了明显的改善。通过对修正后的网格水位进行插值可以得到区域内任一点的潮位值,为近海离岸工程和海上作业提供了精准的潮位信息,解决了临时验潮站布设的难题。
| [1] | 黄祖珂. 潮汐原理与计算[M]. 青岛: 中国海洋大学出版社, 2005. |
| [2] | 刘军. 余水位的主要特性分析及其在海洋测绘中的应用[J]. 测绘通报, 2013(9): 105–107. |
| [3] | 李家彪. 多波束勘测原理技术与方法[M]. 青岛: 海洋出版社, 1999. |
| [4] | 刘雷, 李宝森, 李冬, 等. 基于余水位修正的海洋潮位推算关键技术研究[J]. 海洋测绘, 2012, 32(2): 11–14. |
| [5] | 张双成, 南阳, 李振宇, 等. GNSS-MR技术用于潮位变化监测分析[J]. 测绘学报, 2016, 45(9): 1042–1049. DOI:10.11947/j.AGCS.2016.20150498 |
| [6] | 陈春, 黄辰虎, 王智明, 等. 海道测量中几种水位改正方法的比较与分析[J]. 海洋测绘, 2014, 34(1): 16–20. |
| [7] | 许军, 暴景阳, 刘雁春, 等. 基于区域潮汐场模型的水位控制可行性研究[J]. 海洋测绘, 2011, 31(4): 8–12. |
| [8] | 侯世喜, 黄辰虎, 陆秀平, 等. 基于余水位配置的海洋潮汐推算研究[J]. 海洋测绘, 2005, 25(6): 29–33. |
| [9] | 倪晓东, 邹德华, 邓德标. 薄板样条函数支持下的等深线追踪算法研究[J]. 测绘通报, 2016(1): 132–135. |
| [10] | 黄辰虎, 陆秀平, 申家双, 等. 海道测量水位改正通用模式研究[J]. 海洋测绘, 2011, 31(4): 13–16. |
| [11] | 刘洪博, 潘国富, 应元康, 等. 基于海洋潮汐动力模型的水位改正方法研究[J]. 海洋学研究, 2014, 32(2): 35–39. |
| [12] | 吴頔. 泰国湾潮汐潮流的数值模拟与理论模型研究[D]. 青岛: 国家海洋局第一海洋研究所, 2013. |
| [13] | 桂新, 秦海波, 王胜平, 等. 基于相关系数迭代法的水下地形测量时间延迟探测方法研究[J]. 测绘通报, 2015(5): 57–59, 62. |
| [14] | 许军, 暴景阳, 章传银, 等. 最小二乘水位拟合法的应用优化设置[J]. 海洋测绘, 2016, 36(1): 21–24. |
| [15] | 刘雷, 董玉磊, 曲萌, 等. 基于潮汐模型与余水位监控法的实例分析[J]. 海洋测绘, 2015, 35(4): 36–39. |