2. 精密工程测量实验室, 湖北 武汉 430079;
3. 中建三局第二建设工程有限责任公司, 湖北 武汉 430079
2. Key Laboratory of Precise Engineering and Industry Surveying of SBSM, Wuhan 430079, China;
3. The Second Construction Co. Ltd of China Construction Third Bureau, Wuhan 430079, China
随着经济的快速发展,城市中修建的超高层建筑越来越多。超高层建筑施工过程中,需要将地面控制点逐层向上传递,目前主要是利用激光投点仪将控制点垂直投射到施工所在的顶部楼层。但激光投点仪的投射距离有限,对于超过200 m甚至更高的建筑,需要分段向上传递投点,这会造成投点误差累积,且施工现场环境复杂,投点过程中需要清除大量障碍物,严重影响作业效率,对于夜间工作也存在着安全隐患。
相对于利用激光投点仪进行坐标传递,全球导航卫星系统(GNSS)具有操作简单、精度高、工作效率高、工作时间不受限制等优点[1-2]。北斗导航定位系统(BDS)是我国独立研制的卫星导航定位系统,目前已成功发射23颗卫星,在亚太地区已经具备定位、导航及授时功能(PNT)[3-7],但在工程领域,尤其是超高层建筑监测领域应用还相对较少。
本文以武汉绿地中心超高层建筑项目为依托,采用BDS+GPS技术对激光投点位置进行观测和分析,研究了超高层建筑BDS+GPS相应的数据处理方法。试验结果表明,BDS、GPS、BDS+GPS 3种解算方式的定位结果经垂线偏差改正之后,均可以满足施工需要,一方面较好地对激光投点精度进行了监测,另一方面也验证了我国的BDS系统在超高层建筑施工监测和测量基准传递方面的可行性。
1 数据处理策略 1.1 事后RTK模式处理超高层建筑由于风和日照等作用可能存在摆动,而事后静态处理的前提是所观测的建筑物在观测时段内处于稳定状态[8]。本文通过单历元RTK模式进行解算,可以得到监测点的坐标时间序列,能够较好地评估楼层的稳定性。以地面稳定控制点作为基站,在监测网内选择合适的监测点,利用武汉大学自主研制的GNSS RTK动态数据处理软件进行动态解算,动态数据解算应注意以下两点:
(1) 由于超高层建筑监测网内基线一般为短基线,故采用双频L1、L2无组合观测值进行解算,通过站星双差模式,可以消除钟差及绝大部分电离层误差,考虑到楼层较高,对流层误差难以完全通过双差消除,本文对残余对流层误差采用参数估计进一步削弱其影响[9-10]。
(2) 超高层楼顶观测环境复杂,楼顶施工设备遮挡比较严重,解算时截止高度角设置为10°,考虑到超高层实际摆动情况,在RTK解算过程中,采用单历元独立解算模式。
1.2 事后静态处理静态数据处理主要包括基线解算和网平差两部分,超高层楼顶监测点平面坐标的解算精度主要取决于基线解算的精度。基线解算采用武汉大学自主研制的软件CosaBaseline及由美国麻省理工学院与斯克里普斯海洋研究所联合开发的高精度科研软件GAMIT。
(1) CosaBaseline是单条基线独立解算,可以进行BDS、GPS、BDS+GPS 3种方式的解算,数据处理中,卫星截止高度角设置为15°,观测值采用L1、L2无组合观测值。
(2) GAMIT是科研领域采用的高精度基线解算软件,采用整体网解的方式,且对观测数据中的粗差和周跳作了较好的预处理,具有较高的解算精度和可靠性,解算模式选择适用于短基线的L1, L2_INDEPENDENT(双频观测中独立的L1、L2基线解)[11-13],目前GAMIT还无法解算北斗数据,利用其对GPS数据进行处理得到GPS基线解,作为参考依据。
网平差采用武汉大学自主研制的高精度数据处理软件CosaGPS。首先进行三维无约束平差,得到各点的空间直角坐标;然后进行固定一点一方向二维平差,得到各点在施工坐标系中的平面坐标。
1.3 垂线偏差改正地面一点上的重力向量和相应椭球面上的法线向量之间的夹角定义为该点的垂线偏差。超高层建筑施工是以垂线为依据,楼顶监测点是由激光投点仪在地面沿重力方向垂直投射上去的,而基于GNSS观测值平差得到的监测点的平面坐标是沿法线方向投影到地面施工坐标系的高程投影面。由于超高层建筑顶部高程较大,垂线偏差影响不容忽视,因此需要对平差后的平面坐标进行垂线偏差改正[14-15]。
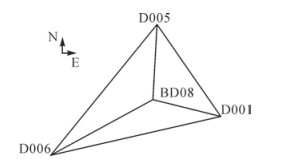
2 试验分析 2.1 数据采集方案本文数据采集于正在施工的武汉绿地中心大楼,分别于2016年1月和6月采集2期数据,同时期的楼高分别为210和310 m,该超高层建筑建成后将达到636 m,是世界第三高楼。试验仪器采用天宝NetR9接收机和大地型天线Zephyr Geodetic model 2,同时接收北斗和GPS数据。试验观测网如图 1所示,其中点D001、D005、D006是位于超高层建筑周围稳定点上的强制对中观测墩;点BD08是位于超高层建筑楼顶的监测点,是激光投点仪投射点。观测网中水平距离最长的基线为D005—D006,长度约为1100 m;水平距离最短的基线为BD08—D001,长度约为370 m。
|
| 图 1 观测网 |
两期数据单历元RTK解算均选取地面控制点D005作为基准站,超高层楼顶监测点BD08作为监测站,按照5 s的时间间隔对GPS数据进行解算,剔除浮点解并采用高阶多项式对北(N)、东(E)坐标时间序列进行拟合,以拟合曲线作为标准,计算两期N、E坐标的中误差,即
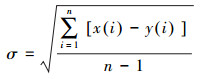 (1)
(1) 式中,σ为坐标中误差;n为解算历元总数;x(i)、y(i)分别为各个历元对应的解算坐标和拟合坐标。
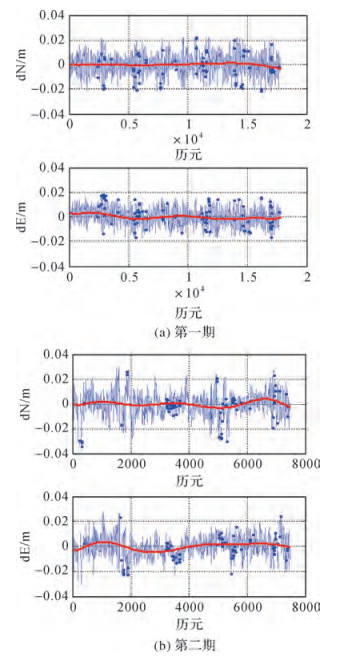
将两期解算与拟合相对应的N、E坐标求差,超过3倍中误差的视为粗差并剔除。图 2为第一期、第二期监测点BD08的N、E坐标在剔除浮点解和粗差并减去平均值后的时间序列图,图中黑色曲线是采用高阶多项式拟合的坐标变化趋势线。
|
| 图 2 监测点N、E坐标变化时间序列 |
从图 2可以看出,两期监测点BD08在监测时间内,N、E坐标整体上在均值上下约2 cm范围内随机波动。经统计,第一期监测点N、E坐标平均值分别为-458.419 5、-14.297 1 m,中误差分别为6.3、5.1 mm;拟合N、E坐标平均值分别为-458.419 5、-14.297 1 m,中误差分别为0.9、1.5 mm,拟合N、E坐标最大值与最小值差值分别为4.7、5.2 mm。第二期监测点N、E坐标平均值分别为-458.424 5、-14.291 7 m,中误差分别为8.0、7.0 mm;拟合N、E坐标平均值分别为-458.424 9、-14.292 3 m,中误差分别为2.6、3.2 mm,拟合N、E坐标最大值与最小值差值分别为10.5、12.9 mm。
综上所述,两期监测点N、E坐标时间序列符合白噪声规律,中误差均在毫米级,拟合趋势线整体上较为平稳。因此可以认为两期观测时间内楼顶监测点位置没有变化,即超高层楼顶是稳定的。
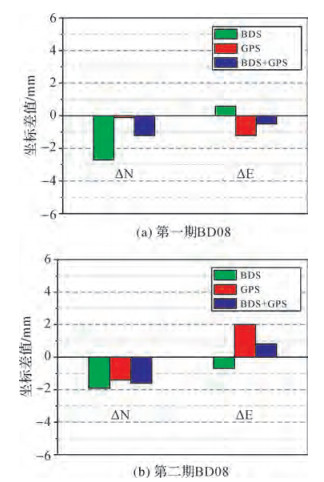
2.3 静态处理结果分析 2.3.1 内符合精度分析将两期超高层楼顶监测点BD08利用CosaBaseline计算的BDS、GPS和组合BDS+GPS 3种模式的定位结果与GAMIT结果进行比较分析,比较结果如图 3所示。从坐标差值结果统计图中可以看出,两期监测点N、E坐标与GAMIT结果差值均小于3 mm,其中第一期采用BDS计算的N坐标差值最大,为-2.7 mm,其他坐标差值均小于2 mm。整体来说,GPS和组合BDS+GPS两种模式定位精度相当,BDS模式稳定性稍差于前两者,3种模式解算结果整体上与GAMIT坐标结果相吻合。
|
| 图 3 CosaBaseline 3种模式结果与GAMIT结果差值统计 |
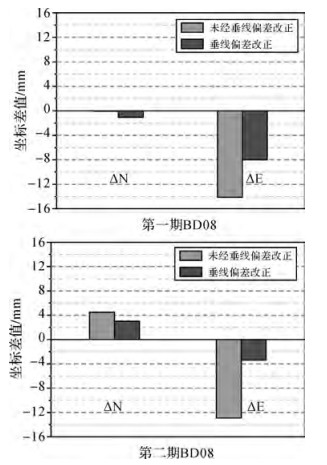
将两期超高层楼顶监测点平差后的平面坐标与对应的地面点已知坐标进行对比分析。超高层建筑所占面积相对较小,属于局部区域,认为该区域内各点垂线偏差相同,根据EGM2008模型计算得到该区域的垂线偏差的南北分量为1.1″,东西分量为-7.0″。将采用单BDS模式计算的监测点BD08在垂线偏差改正前后的坐标与对应的地面点已知坐标进行求差,差值结果统计如图 4所示。可以看出,两期未经垂线偏差改正的N坐标与投点之前已知N坐标的差值分别为-0.1、-4.5 mm,经过垂线偏差改正后差值分别为-1.1、-3.0 mm;两期未经垂线偏差改正的E坐标与投点之前已知E坐标的差值分别为-14.7、-12.9 mm, 均超过了1 cm,经过垂线偏差改正后差值分别为-8.0、-3.4 mm。
|
| 图 4 垂线偏差改正前后北斗系统结果与已知坐标差值统计 |
综上所述,经过垂线偏差改正后的坐标与已知坐标差值均在毫米级,满足工程施工需求,说明利用北斗技术进行超高层建筑基准传递工作具有可行性。
3 结束语本文通过单历元RTK解算,验证了施工中武汉绿地中心超高层楼顶的稳定性。利用BDS、GPS、组合BDS+GPS 3种模式计算了超高层楼顶监测点的坐标,并与GAMIT结果进行了比较,结果表明BDS定位结果稳定性稍差于GPS和组合BDS+GPS定位结果,但也满足超高层楼顶监测要求。此外,超高层楼顶监测点平差后的GNSS平面坐标是沿法线投影到地面控制施工控制网坐标系所在的高程投影面,由于垂线偏差的影响,平差后的施工楼层监测点平面坐标与对应的已知地面点平面坐标之间存在明显差异,需要对平差后的坐标进行垂线偏差改正,改正后坐标与已知坐标差异满足工程施工要求,表明采用北斗技术进行超高层建筑监测和基准传递工作具有可行性。
| [1] | HOFMANN-WELLENHOF B, LICHTENEGGER H, COLLINS J. Global Positioning System[M].[S.l.]:Nova Science Publishers, 2010. |
| [2] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010: 9-14. |
| [3] | 李昕, 郭际明, 周吕, 等. 一种精确估计区域北斗接收机硬件延迟的方法[J]. 测绘学报, 2016, 45(8): 929–934. DOI:10.11947/j.AGCS.2016.20160044 |
| [4] | 于盼, 席瑞杰, 肖玉钢. 北斗卫星导航系统于东北地区高精度变形监测性能分析[J]. 测绘通报, 2016(4): 33–37. |
| [5] | 何俊, 袁小玲, 曾琪, 等. GPS/BDS/GLONASS组合单点定位研究[J]. 测绘科学, 2014, 39(8): 124–128. |
| [6] | LI X, GUO J M, ZHOU L. Preformance Analysis of BDS/GPS Kinematic Vehicle Positioning in Various Observation Conditions[J]. Sensor Review, 2016, 36(3): 249–256. DOI:10.1108/SR-12-2015-0198 |
| [7] | 王仲锋, 林灿, 历亮. 北斗静态定位实验与精度分析[J]. 测绘与空间地理信息, 2014, 37(1): 17–18. |
| [8] | 殷文彦, 黄声享, 刁建鹏. 超高层倾斜建筑周日变形监测数据分析[J]. 测绘信息与工程, 2008, 33(2): 19–21. |
| [9] | 肖玉钢, 姜卫平, 陈华, 等. 北斗卫星导航系统的毫米级精度变形监测算法与实现[J]. 测绘学报, 2016, 45(1): 16–21. |
| [10] | 高兴国, 刘焱雄, 冯义楷, 等. GNSS对流层延时映射函数影响分析比较研究[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1401–1404. |
| [11] | 姜卫平, 赵倩, 刘鸿飞, 等. 子网划分在大规模GNSS基准站网数据处理中的应用[J]. 武汉大学学报(信息科学版), 2011, 36(4): 389–391. |
| [12] | 周命端, 郭际明, 许映林, 等. 水电站GPS变形监测网的数据处理及稳定性分析[J]. 测绘通报, 2011(7): 30–33. |
| [13] | 张双成, 曹海洋, 高涵, 等. 基于GAMIT的GPS短基线解类型分析及应用[J]. 测绘通报, 2011(10): 27–29. |
| [14] | 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉: 武汉大学出版社, 2010: 84-96. |
| [15] | 丁一帆, 李月锋, 丁行斌. 现代大地测量学中的垂线偏差[J]. 大地测量与地球动力学, 2006, 26(2): 115–119. |


