2. 中国测绘科学研究院, 北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
地理国情普查采集的数据包括地理国情要素和地表覆盖图斑两类数据。在对普查成果图进行综合时,地表覆盖图斑化简的一般原则为:图斑轮廓正确反映地表形态特征,并保持图斑轮廓主要转折点位置正确,以及图斑轮廓的弯曲特征和形状,同时还要尽量减少数据的存储量。因此,研究图斑边界的化简方法,保证图面整洁,符合地图制图要求,对地表覆盖图斑综合具有重要的实际意义。
普通地形图综合过程中,呈多边形状的地物类通常比较分散和独立,且多边形的构成与一般曲线类似,都是采用连续坐标序列存储的,对该类图斑的化简一般无需作特殊处理,通常采用曲线化简算法来实现。但地理国情普查成果图中,由于地表覆盖在空间分布上具有全覆盖、无缝隙、无重叠等特征,且具有丰富的属性信息,因此对图斑边界的处理不能简单类同于一般曲线的化简方法,而需要采用顾及图斑空间拓扑关系的化简方法。如果对每个图斑边界进行逐一化简,就会使相邻图斑之间产生缝隙或重叠碎片,从而造成共享边界不一致、无法保持图斑间的拓扑关系的结果,而且还产生人工地物与自然地物难以区分、化简结果不符合实际情况等问题。
本文根据地图制图对图斑的表示要求,在结合考虑各个线要素化简算法的基础上,提出一种基于构建拓扑的图斑化简方法。该方法能够保持原有图斑之间的拓扑关系,并可根据原始数据的属性信息,对构建的拓扑弧段进行分类,通过在地理国情普查图制图综合中对图斑的化简应用,取得了较好的效果。
1 顾及拓扑关系的化简方法 1.1 拓扑关系构建拓扑关系是一种不随空间旋转、平移、缩放等变换而发生改变的定性空间信息,在地图图形的连续变换过程中,其邻接性、包含性、相交性和空间目标的几何类型(点、线、面特征类型)等保持不变。为实现图斑化简时保持拓扑关系不变,需要对原始数据构建拓扑关系。根据文献[1]提出的4-交叉模型,拓扑关系可表示为
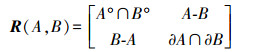 (1)
(1) 式中,A°∩B°表示两面目标A内部与B内部的交集;A-B表示A与B的差集;B-A表示B与A的差集;∂A∩∂B表示A边界与B边界的交集。
从任意的起始弧段开始,搜索该弧段的其他邻近弧段,直至再次搜索到起始弧段,完成对一个多边形的搜索。当地图中所有弧段都完成两个方向的搜索,即生成所有的多边形时,计算所有多边形的面积,并判断其正、负值,以判断属于岛状多边形还是网络状多边形,若为岛状多边形,则需找出其所在的外网络多边形,以此建立完整的多边形拓扑关系[2]。
基于构建的拓扑,拓扑结点可用于对线的追踪,拓扑弧段可用于对点、面的追踪,拓扑岛可用于对线、面的追踪,拓扑面可用于对线、面的追踪。因此,对图斑边界的化简可转化为对拓扑弧段的化简。自然地物图斑的边界一般呈流线性,其化简方法类同于一般曲线。建(构)筑物呈多边形的直角化特征,需要进行特殊的处理。目前,国内外许多学者对线要素化简算法进行了研究,如文献[3]提出的DP算法,文献[4]提出的渐进式化简算法,文献[5]提出的基于客观自然规律的线要素化简算法等;对建(构)筑物多边形的化简领域也取得了一些研究成果[6—10],文献[6—10]通过建立外接矩形或对其凹凸结构的类型判别,实现了呈多边形状的建(构)筑物快速化简,文献[9]采用线型化简方法对三点或多点进行的局部处理拓展为邻近四点,较好地保持了建(构)筑物形态特征。
1.2 保持拓扑关系的化简方法图斑保持拓扑关系的化简是一种基于拓扑构建的方法,其拓扑弧段的结构为:
其中,_LineString表示弧段,_StartNode表示弧段的起始结点,_EndNode表示弧段的终止结点,_LeftPolygon表示弧段的左多边形,_RightPolygon表示弧段的右多边形,_ID表示当前的Feature ID,_Flag表示属性标记。化简的具体技术流程为:
(1) 从设定的起始弧段起始结点开始搜索,根据起始结点与起始弧段依次搜索拓扑多边形组成弧段,并判断弧段左右呈多边形的地物类型。
(2) 若多边形中含有人工地物,则将该弧段类别字段的属性标记为“人工”,否则标记为“自然”,同时将搜索过的弧段指针保存在_TopoArcs容器中,其结点加到等待_TopoNodes容器中。
(3) 遇到单弧或与闭合多边形相连的岛,则退回到上一条弧段,删除_TopoArcs容器和_TopoNodes容器里相应的记录,重新选择搜索的下一条弧段;若满足结束搜索的条件,返回必要的信息。
根据拓扑构建时弧段的分类原则,属于自然类型的采用基于Li-Openshaw的算法进行化简。该方法以人的视觉原理为基础,基于客观综合自然规律的自适应对线状要素进行化简,具体的矢量算法过程为:
(1) 根据比例尺估算目标的圆形SVO(人眼在图上能够分辨的最小目标的直径)的实地距离Fc,其中
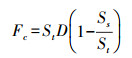 (2)
(2) 式中,St为目标比例尺的分母;Ss为源比例尺的分母;D为最小可视目标SVO的直径。文献[10]建议根据人眼分辨能力取图上(目标比例尺)距离为0.4 mm。
(2) 以曲线起点A为圆心、Fc为半径画圆,与曲线相交于C点,AC的中点作为综合后的选择点。
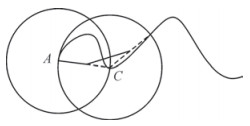
(3) 继续以C点开始,重复步骤(2),直至曲线终点(化简效果如图 1所示)。
|
| 图 1 Li-Openshaw算法化简过程 |
拓扑弧段若为人工类型,则采用基于邻近四点判断其凹凸结构,并以最小可视长度作为阈值,通过对凸凹结构的类型判别与区别处理,来实现呈多边形状的建(构)筑物的化简。
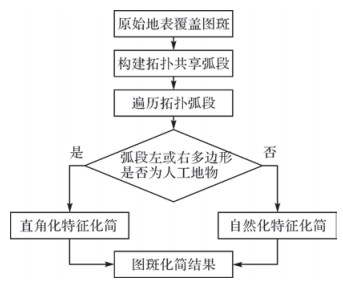
2 实例验证与分析本文以Microsoft Visual Studio2010作为开发环境,利用中国测绘科学研究院自主研制的WJ-Ⅲ无极地图工作站,对本文方法进行实例验证。试验选取某地区1:1万地表覆盖原始图斑作为试验数据,设定图上距离0.4 mm作为最小可视距离。基本试验过程如图 2所示。
|
| 图 2 实例验证流程 |
(1) 对原始图斑数据进行预处理,检查并修正拓扑关系,保证图斑数据无重叠、无缝隙。
(2) 构建拓扑,并根据属性信息对弧段进行区分。
(3) 根据拓扑构建的拓扑弧段,判断弧段是否为人工地物的弧段。若为人工,则采用直角化特征进行化简;若为自然,则采用自然化特征方法对图斑边界进行化简。
(4) 遍历所有弧段,同时对各弧段进行化简处理,试验结果如图 3、图 4所示。
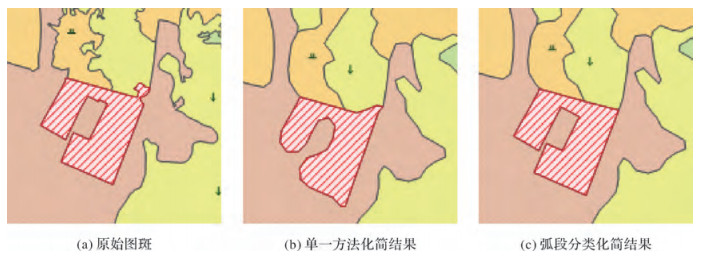
|
| 图 3 弧段分类法的化简结果 |

|
| 图 4 顾及拓扑的化简结果 |
由图 3、图 4的化简结果可以看出,采用分类化简方法对所有弧段进行化简可消除大部分弧段的凹凸部分,较好地体现了整体结构,而且保留了转角处的直角化特征,整体图斑保持了拓扑关系,没有出现缝隙和重叠现象。试验结果表明,顾及拓扑的化简方法可以保持图斑化简前的形态结构,弥补了对各类地物逐一化简方法难以图斑之间拓扑关系的不足。
3 结语本文提出了基于构建空间拓扑关系对地图图斑边界进行化简的方法;并通过共享弧段分类,对不同类型的弧段采用相应的化简方法。该方法可使图斑化简过程中的拓扑关系保持一致,并能够保持图斑化简前后的整体结构。通过在某地区地理国情普查制图综合的实际应用,表明了该方法的有效性。
| [1] | 邓敏, 刘文宝, 冯学智. GIS面目标间拓扑关系的形式化模型[J]. 测绘学报, 2005, 34(1): 85–90. |
| [2] | 程双伟. GIS拓扑关系的建立与更新[D]. 郑州: 信息工程大学, 2002. |
| [3] | DOUGLAS D H, PECUKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Lineor Its Caricatured[J]. The Canadian Cartographer, 1973, 10(2): 112–122. DOI:10.3138/FM57-6770-U75U-7727 |
| [4] | 郭庆胜. 线状要素图形综合的渐进方法研究[J]. 武汉大学学报(信息科学版), 1998, 23(1): 54–58. |
| [5] | LI ZHILIN, OPENSHAW S. Algorithms for Line Generalzation-Based on Natural Objective Principles[J]. International Journal of Geographic Information Systems, 1992, 6(5): 373–389. DOI:10.1080/02693799208901921 |
| [6] | 郭庆胜. 以直角方式转折的面状要素图形简化方法[J]. 武汉测绘科技大学学报, 1999, 24(3): 255–258. |
| [7] | 郭仁忠, 艾廷华. 制图综合中建筑物多边形的合并与化简[J]. 武汉测绘科技大学学报, 2000, 25(1): 25–30. |
| [8] | 艾廷华, 郭仁忠, 陈晓东. Delaunay三角网支持下的多边形化简与合并[J]. 中国图象图形学报, 2001, 6(7): 703–709. DOI:10.11834/jig.200107153 |
| [9] | 许文帅, 龙毅, 周侗, 等. 基于邻近四点法的建筑物多边形化简[J]. 测绘学报, 2013, 42(6): 929–936. |
| [10] | 陈文瀚, 龙毅, 沈婕, 等. 利用约束D-TIN进行建筑物多边形凹部结构识别与渐进式化简[J]. 武汉大学学报(信息科学版), 2011, 36(5): 584–587. |
| [11] | MULLERJ C. Fractal and Automated Line Generalization[J]. The Cartographic Journal, 1987, 24(1): 27–34. DOI:10.1179/caj.1987.24.1.27 |




