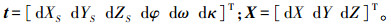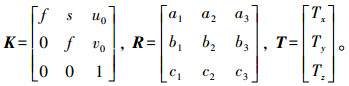2. 江苏师范大学测绘学院, 江苏 徐州 221008
2. School of Geodesy and Geomatics, Jiangsu Normal University, Xuzhou 221008, China
解析空中三角测量(又称摄影测量加密)是摄影测量内业测图和数字产品生成的第一道工序,其核心内容是以像片上的像点坐标为依据,用摄影测量的方法求解测区中所有影像的外方位元素,并基于摄影过程的几何反转,重建可量测的几何立体模型,然后解求出地面点的空间坐标[1]。由于无人机有作业费用低廉、作业方便及受气候条件限制少等优点,已广泛应用于摄影测量、土地用途调查等诸多领域。但是,无人机由于重量较轻,体积小,非常容易受气流干扰,飞行稳定性较差,航线保持较困难[2]。所拍摄的航摄影像相对于常规航空摄影像片旋偏角大、航线弯曲度大、影像重叠度不规则等,从而导致无人机机载POS系统定位定姿偏差较大[3],尤其在用于精度要求较高的大比例尺航空摄影测量领域时, 其后续摄影测量空三加密成果的精度将会受到不同程度的影响[4],是失败。
20世纪80年代后期兴起的GPS辅助空中三角测量技术[5]可大量减少甚至完全不使用地面控制点来进行摄影测量加密,以获取航测成图所需的图根控制点。尽管基于差分GPS定位(DGPS)[6]的空中三角测量技术在常规航空摄影测量中已被广泛应用,在我国的传统航测4D产品生产和西部测图困难区域的地形测绘中发挥了重要作用,但对于低空摄影测量数据的处理尚处于实验阶段,且DGPS系统的引入增加了系统成本、野外基站的布设及测量方面的工作。另一方面,GPS接收机在无人机高速飞行条件下容易发生信号失锁或周跳,定位结果易受影响[7]。
源于计算机视觉领域的多视几何(multiple-view geometry)[8]与传统摄影测量在很多方面有极大的相似性。多视几何由于对初始条件要求很低,因此对硬件条件及数据获取条件要求也很低。然而,多视几何理论与传统摄影测量理论并不完全一致,两者仍存在一定的差异。如何将多视几何理论引入传统摄影测量加密,使多视几何理论弥补传统摄影测量理论的不足与局限性,无疑具有重要的实践意义。
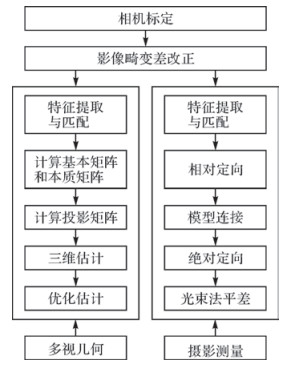
1 多视几何理论辅助的空三加密 1.1 二者的差异在已标定相机的前提下,给出摄影测量和多视几何的技术流程,如图 1所示。
|
| 图 1 多视几何与摄影测量空三加密技术流程 |
由图 1可以看出,多视几何与传统摄影测量的基本目的是一致的,即都是通过二维序列影像重建三维模型(相关技术细节详见文献[9],在此不再赘述)。但二者也存在一定的差异,从对最终测量成果精度的影响来看,主要包括:
(1) 算法差异:由于摄影测量源于测绘学科,测量数据处理方法——最小二乘迭代求解几乎贯穿于摄影测量的全过程;而计算机视觉更强调矩阵分解,总是设法将非线性问题转化为线性问题,尽可能避免求解非线性方程。因而,摄影测量较多视几何具有更高的定位精度。
(2) 初始数据:摄影测量利用最小二乘原理进行求解,因此所求未知数必须具有良好初始值。这些初始值通常与飞机拍摄瞬间的姿态和方向有关,而无人机机载POS定位定姿系统通常偏差较大,从而造成非线性最小二乘求解的困难;而多视几何理论并不要求未知数具备初始值,因为多视几何理论的已知数据仅需要影像上特征像点的像素坐标。
(3) 像点坐标观测值精度:多视几何中的立体影像匹配技术成果颇丰,但大多强调匹配结果的稳健性,如新近发展的基于块匹配技术的多视立体(patch-based multi-view stereo)[10],这些匹配方法在精度上尚低于如摄影测量领域所常用的最小二乘匹配技术。
基于以上的分析可知,多视几何技术对影像拍摄位置和方向无需严格约束,具有很好的鲁棒性和稳健性,其优化结果恰好为摄影测量加密提供了良好的初始数据。这也是二者可进行有效融合的理论和现实基础。
1.2 多视几何理论辅助的空三加密传统摄影测量加密采用理论较为严密的光束法区域平差,其使用的函数模型为共线方程
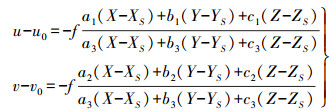 (1)
(1) 式中,(u, v)为像点坐标;(u0, v0)为像主点坐标;f为相机焦距;(X, Y, Z)为像点对应的物方空间点坐标;(XS, YS, ZS)为相机外方位元素的3个线元素;ai、bi、ci(i=1, 2, 3) 为外方位元素的3个角元素(φ,ω,κ)构成的旋转矩阵。
式(1) 线性化后得到
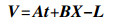 (2)
(2) 式中
其他各项参数的含义详见文献[11]。式(2) 的求解需要良好的初始值,可以通过多视几何技术获得,如下。
设以齐次坐标表示的空间点为Si(Xi, Yi, Zi, 1),投影点为si(ui, vi, 1),投影矩阵为P,则有
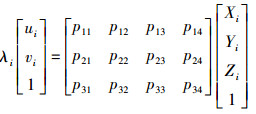 (3)
(3) 投影矩阵P包含11个自由变量,又可分解成为旋转矩阵R、平移矩阵T和相机检校矩阵K
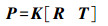 (4)
(4) 式中,λi为比例因子。
式中,f为相机焦距;s为透镜畸变参数;Tx、Ty、Tz为投影中心在世界坐标系下的坐标分量,其他参数的含义同式(1)。
基于式(3) 的结果可为式(2) 提供待求参数初始值。更进一步的,式(3) 的结果还可以再迭代优化。
不失一般性,假设摄影测量区域网(计算机视觉一般称之为影像场景)中共有n个三维空间点在m张相片中可见并令xij为第i个像点在第j张影像上的像点坐标,设定一个二进制变量vij,如果第i个像点在第j张影像上可见,则vij=1,否则vij=0;令aj表示相机参数,bj表示一个三维空间点,则多视几何采用的光束法平差即是按下式最小化通过三维空间点和相机参数计算得到的像点的重投影误差
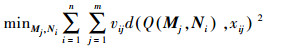 (5)
(5) 式中
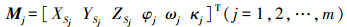
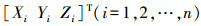
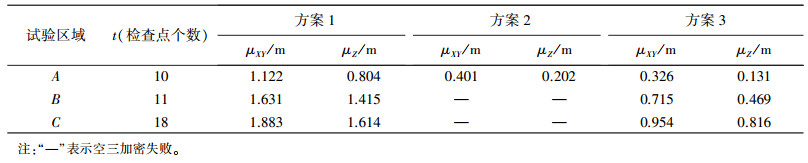
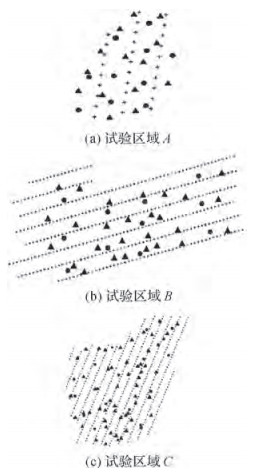
选择了不同地面分辨率及不同地形特征的3块区域(简记为A、B、C)开展试验(详见表 1)。A区域为平坦地形,地面高程约为45 m,共3条航带30张影像,覆盖面积约1.3 km2,布设了24个像控点,其中10个为检查点;B区域为丘陵地形,地面高程1300~1500 m,共8条航带392张影像,覆盖面积约10 km2,布设了38个像控点,其中11个为检查点;C区域为高山地地形,地面高程1300~2100 m,共14条航带520张影像,覆盖面积约16.5 km2,布设了72个像控点,其中18个为检查点。各区域航线布设及像控点分布如图 2所示,图中三角形为像控点,圆形为检查点,其余为航点。3个测区的无人机航摄参数见表 1。
|
| 图 2 各区域航线布设及像控点分布 |
多视几何和摄影测量加密算法分别选用目前使用较为广泛的Agisoft PhotoScan[12]和Inpho[13]软件系统。PhotoScan基于计算机视觉最新的多视图三维重建技术对序列立体影像进行全自动化的处理,也可以通过给予的控制点生成测量坐标系统下的真实坐标的三维模型[14]。Inpho对于各种航空框幅式相机、数字框幅式CCD相机、推扫式ADS40相机甚至无人机承载的数码相机等获取的影像均可实现完全自动化的高效空三处理,其用于空三加密处理的模块为MATCH-AT,该模块采用光束法区域网平差模型进行平差解算,其自动化的最小二乘匹配技术精度较高[15]。
2.2 试验结果及分析试验及分析主要是基于像控点采用不同的摄影测量加密方案完成空三加密,继而在各试验场地中布设的像控点中选取t个点,比较其GPS测量坐标与立体模型中的人工测量坐标的较差Δi(i=X, Y, Z)并计算其中误差,即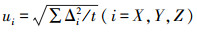
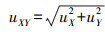
图 3和图 4分别给出了各区域采用方案1和方案3空三结果的图形显示;表 2给出了方案1和方案3空三外方位差值统计;表 3给出了各区域采用方案1和方案2和方案3的检查点立体量测精度统计;图 5所示为试验区域A检查点高程误差统计折线图(分析X、Y坐标误差分布,具有类似规律,因篇幅所限,这里未全部绘出)。

|
| 图 3 各区域方案1的空三结果 |

|
| 图 4 各区域方案3的空三结果 |
|
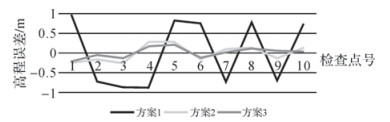
| 图 5 试验区域A检查点高程误差统计折线图 |
以上试验结果表明:
(1) 方案1(基于PhotoScan的摄影测量加密)得到的外方位元素与方案3(多视几何辅助的摄影测量空三加密)得到的外方位元素比较接近。两种方案获得的线元素差值均小于1 m,角元素差值均小于0.1°,因此将方案1得到的结果作为方案3的初始值具有很高的精度。
(2) 针对各区域检查点立体量测精度,比较方案1和方案3可以看出方案3精度更高。对于试验区域B和C,方案2(基于Inpho的摄影测量空三加密)结果失败,可以看出方案3可靠性更高。
(3) 从图 5可以看出,对于试验区域A,方案1得到的检查点高程误差较大,比较方案2和方案3可以看出方案3得到的检查点高程误差较小,因此方案3空三加密精度更高。
3 结语多视几何理论及其技术的发展为传统摄影测量领域提供了新的发展方向,针对无人机本身质量轻、载荷低,自带的POS数据精度不高等问题,其后续摄影测量空三加密成果的精度将会受到不同程度的影响,甚至失败。本文提出了将多视几何理论引入传统摄影测量的方案,采用不同地面分辨率和不同地形特征的多个测区试验,结果表明该方案能提高无人机低空摄影测量空三加密的可靠性和立体量测精度。
| [1] | 杨莉. POS辅助下Inpho软件空三加密研究及精度分析[J]. 科技创新导报, 2013(11): 25–26. DOI:10.3969/j.issn.1674-098X.2013.11.017 |
| [2] | 廖永生, 周宏霞. DGPS差分定位系统应用于低空摄影测量无人机气动参数计算[J]. 测绘与空间地理信息, 2011, 34(1): 121–123. |
| [3] | 任志明, 李永树, 何敬, 等. 基于姿态数据的无人机影像自动刺点功能研究[J]. 测绘通报, 2011(4): 44–46. |
| [4] | 程婷婷, 方源敏, 贾培哲. 提高我国西南地区空三加密精度的几种方法[J]. 测绘与空间地理信息, 2014(4): 216–218. |
| [5] | 石平, 张文安. IMU/GPS辅助航空摄影测量技术方法应用研究——以贵阳市航空摄影测量项目为例[J]. 测绘通报, 2016(1): 88–90. |
| [6] | GUO D H, WU L X, WANG J C, et al. The Application of IMU/DGPS-supported Photogrammetry[J]. Remote Sensing for Land & Resources, 2006, 18(1): 51–55. |
| [7] | 韩厚增, 王坚, 李增科. GPS/INS紧组合的INS辅助周跳探测与修复[J]. 测绘学报, 2015, 44(8): 848–857. DOI:10.11947/j.AGCS.2015.20140350 |
| [8] | ANDREW A M. Multiple View Geometry in Computer Vision[J]. Kybernetes, 2001, 30(9/10): 1865–1872. |
| [9] | 邓非, 张祖勋, 张剑清. 基于序列影像的城市三维建模[J]. 计算机工程, 2007, 33(8): 208–209. |
| [10] | SHEN S. Accurate Multiple View 3D Reconstruction Using Patch-based Stereo for Large-scale Scenes[J]. IEEE Transactions on Image Processing, 2013, 22(5): 1901–1904. DOI:10.1109/TIP.2013.2237921 |
| [11] | 吴巍, 魏富恒, 高振东, 等. 基于四元数的共线条件方程线性化[J]. 测绘科学, 2009(S2): 94–95. |
| [12] | 张小宏, 赵生良, 陈丰田. Agisoft photoscan在无人机航空摄影影像数据处理中的应用[J]. 价值工程, 2013(20): 230–231. DOI:10.3969/j.issn.1006-4311.2013.20.124 |
| [13] | MA D L, CUI J, DING N. The Making of Digital Orthophoto Map Based on INPHO[J]. Applied Mechanics & Materials, 2011, 90-93: 2818–2821. |
| [14] | 李秀全, 陈竹安, 张立亭. 非量测相机影像三维模型构建及精度检验[J]. 测绘科学, 2016, 41(6): 144–147. |
| [15] | 黎治坤, 郑史芳, 刘锐, 等. 几种无人机正射影像处理软件的比较[J]. 测绘通报, 2016(6): 82–86. |