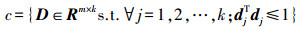2. 地理国情监测国家测绘地理信息局工程技术研究中心, 陕西 西安 710054
2. Engineering Research Center, Geographical Conditions Monitoring National Administration of Surveying, Mapping and Geoinformation, Xi'an 710054, China
在图像数据采集过程中,由于图像传感器、光学仪器设备及拍摄条件的限制,图像的空间分辨率在采集阶段提高渐难,但在众多图像应用领域,对图像空间分辨率的要求仍在提高。航空航天遥感正向高空间分辨率、高光谱分辨率、高时间分辨率、多极化、多角度的方向迅猛发展,为提高遥感影像空间分辨率,影像超分辨率重建技术成为一个颇具潜力的研究方向[1]。超分辨率重建技术(super resolution reconstruction, SRR)可通过对一幅或多幅低分辨率(low resolution, LR)的图像进行学习得到一幅高分辨率(high resolution, HR)的图像,并且该方法成本低廉,重建后空间分辨率提升效果明显[2]。随着压缩感知和机器学习技术的不断提高,基于学习的超分辨率重建方法已成为研究热点。此类方法主要是通过训练学习与输入影像相似的影像构成的训练样本数据,得到高低分辨率影像之间的关系,由先验知识推广用于类似的低分辨率影像的超分辨率重建。Freeman等[3]最早提出了基于样例学习的超分辨率算法,其基本思想是利用马尔可夫随机场描述输入图像中的图像块与示例样本块之间的匹配条件,最终生成高分辨率图像。Bishop等[4]对Freeman提出的方法作了一些改进,在图像块合并方面提出了新方法,提高了对应图像块的匹配速度。Jeong等[5]设计了K-means聚类字典,实现了快速的学习类SRR。Kim等[6]采用自适应的残差信息和图像块可信度提升了基于学习的SRR。Pu和Zhang等[7]提出了交互式领域嵌入(K-nearest neighbor, K-NN)的SR方法。近年来,随着压缩感知理论和稀疏表示模型的技术发展,Yang等[8-9]提出了一种基于稀疏表示的超分辨率算法(super-resolution via sparse representation, ScSR),通过联合训练两个高低分辨率图像块的过完备字典,利用L1正则优化进行稀疏编码,获得了较好的重建效果。Zeyde等[10]对Yang的方法作了改进,对训练样本集作了主成分分析(principal component analysis,PCA)以降低数据维度,有效地提高了运算效率。Mairal等[11]提出了在线字典学习的稀疏表示算法,该方法允许样本进行分批处理,显著降低了样本集的数量,自适应输入图像,且及时引入图像退化信息并更新字典原子,对基于超完备字典的应用有重要意义。
随着稀疏编码理论的发展,字典学习方法的研究成为稀疏表示理论的重要组成部分。目前,主要的字典学习方法有:Engan等[12]最早提出的最优方向方法(method of optimal directions, MOD)、Aharon等[13]提出的快速奇异值分解方法(K-SVD)、Lee等[14]提出的FSS(the feature sign search)方法、Mairal等[15]提出的在线字典更新方法(online dictionary learning, ODL)等。本文针对地物特征复杂、数据量巨大的遥感影像,深入研究了基于字典学习类算法的基本原理及优缺点。此外,本文根据遥感影像的特点,使用同一数据源进行字典学习,利用不同字典学习算法分别生成高、低联合字典对,采用不同尺寸大小及不同缩放倍数的测试图像,进行超分辨率重建,依据重建图像综合分析各种算法的重建性能、鲁棒性和复杂度,进一步研究针对遥感影像数据不同应用需求各种算法的适用性。
1 字典学习基本理论通常对于图像信号x ∈ RN,可以由过完备字典D =[d1 d2…dM]∈ RN×M(M>N)稀疏表示为
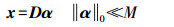 (1)
(1) 式中,α =[α1 α2…αM]T∈ RM,为稀疏表示系数。
对于图像SRR过程来说,关键是字典的构建。理想的字典使得稀疏系数求解过程更加快捷,并能简洁准确地表达图像。基于学习的过完备字典构建方法主要采用了机器学习的思想,通过对样本学习,构造出具有某种针对性的学习字典,从而更加准确地对图像进行稀疏表示[16]。设X =[x1 x2 … xM]为样本组成的矩阵,A =[α1 α2 … αM]为稀疏表示系数矩阵,其中M为样本个数。若T表示预设的非零元素的最大值,即可以容忍稀疏度的最小值,则学习字典的优化更新问题可采用下式进行求解
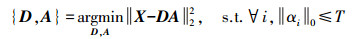 (2)
(2) 由式(2) 可知,字典学习就是已知X求解D与A的过程。而D和A为两个需要更新的变量,因而此问题属于非凸问题。对于此类问题,通常可采取交替优化的方法进行求解。该方法分为两步:第一步初始化一个过完备字典,通过稀疏表示优化算法对稀疏系数进行求解;第二步根据得到的稀疏表示系数,对初始字典的原子进行更新。交替迭代上述两步骤,得到优化解。其中第一步的稀疏表示优化算法有基追踪算法、匹配追踪算法等,由于正交匹配追踪算法(OMP)及其扩展算法收敛性较好,成为求解此类问题的首选[17]。OMP算法是通过每次迭代选择一个局部最优解来逐步逼近原始信号,首先采用相关性原则搜索字典中与残差量最相关的一列原子,然后将已选的原子进行Gram-Schmidt正交化处理,计算出最优稀疏系数,并更新残差,经逐次迭代求解得到字典的最优稀疏表示系数。第二步采用字典更新算法来更新优化字典原子,现阶段常用的更新算法有:MOD算法、K-SVD算法、ODL算法、主分量分析算法(PCA)及广义PCA(generalized PCA, GPCA)[18]等。其中GPCA是通过降维字典空间进行逼近求解,适用于与其他稀疏表示方法结合使用,本文不作详细介绍。
2 字典学习类算法 2.1 MOD算法MOD算法是通过对样本图像块的字典表示进行求解,并判断误差大小迭代更新字典,获得最优字典。数学定义的目标函数如式(2) 所示,实现过程首先是随机生成初始字典D0,迭代次数k初始值为1,每次迭代完成后增加1。迭代开始首先固定字典D,利用基匹配追踪算法求稀疏系数的逼近解
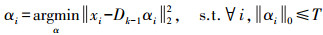 (3)
(3) 式中,αi为样本图像块关于字典的稀疏表示系数,即A =[α1 α2 … αi … αM]。将上式求得的A用于下式,更新字典原子
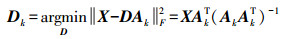 (4)
(4) 式中,Dk为第k次更新后得到的字典;Ak为第k次更新前的稀疏系数阵。经过多次迭代,当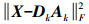
K-SVD算法本质与MOD算法相近,均采用交替迭代,先求解稀疏系数再更新字典。与MOD算法的不同之处在于更新字典时,采用奇异值分解方法逐个更新字典中的原子,完成更新需要进行k次分解。具体流程如下所述。
训练样本优化更新字典问题是求解式(2) 的问题,首先初始化字典D0,但对D0的每个原子作归一化;其次,固定字典D,采用基追踪算法求解稀疏分解因子αi;最后利用稀疏分解因子依次修正字典原子,定义样本集为Ωj0,字典原子为dj0,其中Ωj0={i|1≤i≤M,Ak[dj0, i]≠0}。
由式(2) 可得误差矩阵Ej0
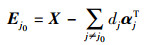 (5)
(5) 通过式(5) 选择Ej0与Ωj0相一致的列,得到ERj0。对矩阵ERj0进行奇异值分解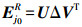
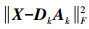
针对训练样本集大而导致字典学习效率不高的问题,Mairal等提出了在线字典学习算法。该算法基于随机逼近理论,可扩展实现不确定和大型数据集训练样本的学习,提高了字典训练的精度。其具体过程如下:
在初始化阶段,待训练的图像块为X,随机设置初始字典为D0,同时对At、Bt进行初始化设置:A0←0、B0←0。利用LARS稀疏编码计算稀疏系数
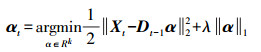 (6)
(6) 其次,对At、Bt进行更新,为了算法的加速收敛,每次迭代选择η>1个信号,则第t次迭代包含的信号可表示为xt, 1, …, xt, η,利用下式迭代更新At、Bt:
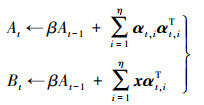 (7)
(7) 式中,β值的设置为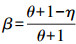
通过Dt-1,利用式(2) 计算并更新Dt
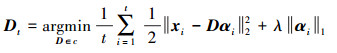 (8)
(8) 式中,c为字典D的约束条件
由于待求的Dt与式(8) 中的第二项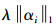
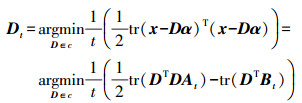 (9)
(9) 为满足约束条件D ∈c,必须对字典D逐列进行更新,采用牛顿迭代法对每列字典元素进行更新,共迭代t次,生成字典D,其重建所需的高低分辨率字典Dh、Dl均按照上述过程联合生成。该算法在联合字典的学习过程中,同时训练Dh、Dl可保证其在误差条件的约束下,生成最优的联合字典。同时将重建过程与字典学习阶段的正则化参数看作独立量,分别进行设置,这样可灵活调整字典学习阶段和重建阶段的稀疏表示误差,以获得最佳的超分重建效果。
3 试验结果及分析针对上述3种字典学习方法的分析,为验证其在不同图像大小下的重建性能差异,训练样本为100幅不同大小的遥感影像,采用5×5的低分辨率图像块和相应的10×10的高分辨率图像块提取特征,其中字典大小均设为2048,重叠像素设置为4。对于同一训练样本字典学习过程,ODL算法运行时间最短,500次迭代用时1 618.7 s,K-SVD算法50次迭代用时2 750.2 s,MOD算法最慢,50次迭代用时8 475.9 s。文中学习得到的字典均采用稀疏表示方法,利用L1范数求解得到稀疏系数,并与高分辨率字典结合重构得到高分辨率图像。
试验选取5幅不同像素大小同类地物的资源三号正射影像作为测试影像,比较不同算法的字典学习时间,并选取其中一幅影像进行不同缩放倍数的重建,比较3种算法的重建结果。为对各种算法的重建效果进行定量评价,测试影像由高分辨率影像降采样得到。以高分辨率影像作为参考影像,采用峰值信噪比PSNR作为定量评价指标。
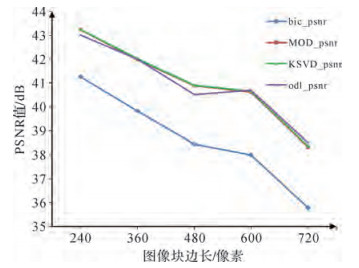
5幅测试图像均为正方形,边长分别为240、360、480、600、720像素,地物类型均为建筑物。试验结果如图 1所示,随着测试图像尺寸的增大,3种基于学习的超分辨率重建算法其重建结果的定量评价值相比于插值方法,其差值在逐渐增大,证明了在图像尺寸增大后,基于学习的方法重建效果远优于插值方法。在3种基于学习的超分辨率算法中,K-SVD算法的平均PSNR值仅比MOD算法高0.02 dB,而对于不同大小的图像,ODL算法的PSNR值时高时低,图像大小为480时,ODL算法的比MOD低0.36 dB,但随着图像尺寸的增大,ODL算法重建图像的PSNR值与K-SVD和MOD算法的值相近,且有高于两者的趋势。
|
| 图 1 不同图像大小各算法PSNR值 |
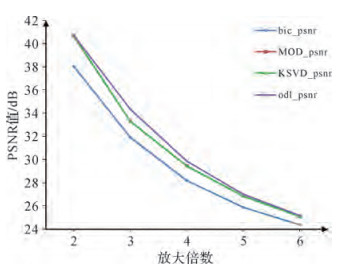
图 2显示了在不同的超分辨率重建放大倍数下,3种算法重建图像的PSNR值折线图,图 3显示了边长为600像素的测试图像进行3倍重建时几种算法的重建结果。由图 2显示,3种算法重建结果均优于插值方法,K-SVD与MOD算法重建图像PSNR值几乎一致,ODL算法重建图像PSNR值均高于K-SVD和MOD算法,平均PSNR高约0.36 dB左右,且在3倍放大时,ODL算法的PSNR值比MOD算法高1.08 dB。随着放大倍数的不断增大,基于学习的重建图像质量与插值图像质量无较明显的差别,其原因是放大倍数较大时,将字典用于稀疏重建,其稀疏表示误差增大,高频细节信息丢失过多,致使重建质量下降;可通过调节重建时的正则化参数,或融入残差高频信息进行重建,以提高遥感影像的重建质量[19-20]。由图 3显示,3倍重建时不同算法在建筑物及道路边缘清晰度不同,而ODL算法恢复了更多的细节信息,重建效果相对最优,其重建影像更加清晰,纹理边缘明显,总体来看各算法的重建视觉效果与PSNR指标评价值相一致。
|
| 图 2 不同放大倍数各算法PSNR值 |

|
| 图 3 同一测试影像3倍重建结果 |
本文对基于学习的3种超分辨率算法即MOD、K-SVD、ODL字典学习算法进行了梳理,介绍了各种算法的原理及优缺点。针对遥感影像的超分辨率重建,选取了PSNR值与运行时间作为3种字典学习方法重建质量的评价指标,通过对比试验发现,对于数据信息量较大的遥感影像,选择ODL在线字典学习的超分辨率重建方法,重建性能稍高于其余两种方法,但对于不同大小的图像进行超分辨率重建,ODL算法稳定性较差。此外,当放大倍数逐渐增大时,3种方法重建影像的质量都在降低,需要进一步改进重建阶段的算法,减小稀疏表示误差,更加有效地进行遥感影像的超分辨率重建。
| [1] | 李德仁, 童庆禧, 李荣兴, 等. 高分辨率对地观测的若干前沿科学问题[J]. 中国科学(地球科学), 2012(6): 805–813. |
| [2] | 钟九生. 基于稀疏表示的光学遥感影像超分辨率重建算法研究[D]. 南京: 南京师范大学, 2013: 1-14. |
| [3] | FREEMAN W T, JONES T R, PASZTOR E C. Example-based Super-resolution[J]. IEEE Computer Graphics and Applications, 2002, 22(2): 56–65. DOI:10.1109/38.988747 |
| [4] | BISHOP C M, BLAKE A, MARTHI B. Super-resolution Enhancement of Video[C]//AISTATS.[S.l.]:[s.n.], 2003. |
| [5] | JEONG S C, SONG B C. Fast Super-resolution Algorithm Based on Dictionary Size Reduction Using k-means Clustering[J]. ETRI Journal, 2010, 32(4): 596–602. DOI:10.4218/etrij.10.0109.0637 |
| [6] | KIM C, CHOI K, RA J B. Improvement on Learning-based Super-resolution by Adopting Residual Information and Patch Reliability[C]//2009 16th IEEE International Conference on Image Processing (ICIP).[S.l.]:IEEE, 2009:1197-1200. |
| [7] | PU J, ZHANG J, GUO P, et al. Interactive Super-resolution through Neighbor Embedding[C]//Asian Conference on Computer Vision. Berlin:Springer Berlin Heidelberg, 2009:496-505. |
| [8] | YANG J, WRIGHT J, HUANG T, et al. Image Super-resolution as Sparse Representation of Raw Image Patches[C]//IEEE Conference on CVPR 2008.[S.l.]:IEEE, 2008:1-8. |
| [9] | YANG J, WRIGHT J, HUANG T S, et al. Image Super-resolution via Sparse Representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861–2873. DOI:10.1109/TIP.2010.2050625 |
| [10] | ZEYDE R, ELAD M, PROTTER M. On Single Image Scale-up Using Sparse-representations[C]//International Conference on Curves and Surfaces. Berlin:Springer Berlin Heidelberg, 2010:711-730. |
| [11] | MAIRAL J, BACH F, PONCE J, et al. Online Learning for Matrix Factorization and Sparse Coding[J]. Journal of Machine Learning Research, 2010, 11(1): 19–60. |
| [12] | ENGAN K, AASE S O, HUSOY J H. Method of Optimal Directions for Frame Design[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing.[S.l.]:IEEE, 1999, 5:2443-2446. |
| [13] | AHARON M, ELAD M, BRUCKSTEIN A. The K-SVD:An Algorithm for Designing of Overcomplete Dictionaries for Sparse Representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311–4322. DOI:10.1109/TSP.2006.881199 |
| [14] | LEE H, BATTLE A, RAINA R, et al. Efficient Sparse Coding Algorithms[C]//Advances in Neural Information Processing Systems.[S.l.]:[s.n.], 2006:801-808. |
| [15] | MAIRAL J, BACH F, PONCE J. Task-driven Dictionary Learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(4): 791–804. DOI:10.1109/TPAMI.2011.156 |
| [16] | 李珅. 基于稀疏表示的图像去噪和超分辨率重建研究[D]. 西安: 西安光学精密机械研究所, 2014. |
| [17] | 杨真真, 杨震, 孙林慧. 信号压缩重构的正交匹配追踪类算法综述[J]. 信号处理, 2013, 29(4): 486–496. |
| [18] | VIDAL R, MA Y, SASTRY S. Generalized Principal Component Analysis (GPCA)[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(12): 1945–1959. DOI:10.1109/TPAMI.2005.244 |
| [19] | 倪浩, 阮若林, 刘芳华. 基于双正则化参数的在线字典学习超分辨率重建[J]. 计算机应用研究, 2016, 33(3): 277–281. |
| [20] | ZHANG J, ZHAO C, XIONG R, et al. Image Super-resolution via Dual-dictionary Learning and Sparse Representation[C]//2012 IEEE International Symposium on Circuits and Systems.[S.l.]:IEEE, 2012:1688-1691. |