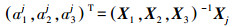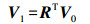Download PDF  
文章快速检索  
  高级检索
引用本文
李艳焕，徐振亮，邵良杉。一种新的影像位姿直接估计方法[J]. 测绘通报，2017(6)：17-20. DOI: 10.13474/j.cnki.11-2246.2017.0181.
LI Yanhuan, XU Zhenliang, SHAO Liangshan. A Novel Direct Estimation Method for Image Pose[J]. Bulletin of Surveying and Mapping, 2017(6): 17-20. DOI: 10.13474/j.cnki.11-2246.2017.0181.
一种新的影像位姿直接估计方法
李艳焕1, 徐振亮2, 邵良杉1     
1. 辽宁工程技术大学系统工程研究所, 辽宁 阜新 123009;
2. 中国资源卫星应用中心, 北京 100094
收稿日期：2016-10-23; 修回日期：2017-01-13
基金项目：国家自然科学基金（71371091）
作者简介：李艳焕(1979-), 女, 博士, 工程师, 主要研究方向为计算机视觉、数据分析及处理。E-mail:lyh09523162@163.com
通讯作者：徐振亮。E-mail:xuzhenliang@pku.edu.cn
摘要：针对影像位姿耦合不易直接求解的问题，建立了一种高精度分层位姿参数估计的方法。首先，通过选择3点构成面积最大的像点对应的物点作为基点，经投影方程的改化形式方程，得到估计深度及平移信息；然后利用旋转矩阵保范性获得相机外参线元素尺度参数；最后，将问题转化为由向量估计旋转关系问题，利用Procrustes理论得到外参角元素的最佳估值。该方法可有效解决该深度与耦合位姿参数难以处理的问题。试验证明，此方法确定的位姿参数估计模型形式简洁，容易收敛，参数估计精度较直接对投影矩阵分解方法质量要高。
关键词：齐次坐标     直接线性变换     基点     Procrustes     位姿估计    
A Novel Direct Estimation Method for Image Pose
LI Yanhuan1, XU Zhenliang2, SHAO Liangshan1    
1. System Engineering Institute, Liaoning Technical University, Fuxin 123009, China;
2. China Centre for Resources Satellite Data and Applications, Beijing 100094, China
Abstract: In order to solve the problem of image pose coupling calculating, this paper has established a high-precision hierarchical estimated pose parameters of image. Firstly, we select corresponding three image points of 3D points which constitute the largest area in image as a base to estimate the depth and translate information. Then based on the above method, we obtain the scale parameter of camera exterior information. Finally, the topic is transformed to a problem of estimating rotation relationship by vector, using Procrustes theory to obtain the best estimation of the angle elements of external parameters. The method can effectively solve problems which depth and coupling pose parameters can not deal with. Experimental results show that this method of determining position and orientation parameter estimation model is of briefness, easy convergence and it can also achieve higher parameter estimation accuracy than the direct projection matrix factorization.
Key words: homogeneous coordinates     direct linear transformation (DLT)     base point     Procrustes method     pose estimation    

图像位姿估计是计算机视觉及摄影测量学研究领域中的重要课题[1-2]，贯穿航空航天测绘整个学科，研究精度高、速度快的影像位姿算法具有十分重要的理论与现实意义。姿态估计常常采用迭代解法和直接解法两种方法。迭代解法在摄影测量领域有广泛应用，其解算精度高，具有很好的几何意义，解算的结果准确度比较均匀，是一种严密的方法，但其缺点是运算量大[3]，并且需要位姿初值。在没有初值的情况下，直接解法可以直接求解位姿参数，主要指直接线性变换(DLT)法，它是建立像点坐标和同名物方点坐标之间的直接线性关系，并采用最小二乘法获得最小代数误差解，由于不需要外参数(外方位元素)的初始近似值，如近景非量测数码影像或无人机影像处理[4-5]，因此具有解算速度快等优点，但同时具有解算精度不高且参数没有明确几何意义的缺点，该方法作为迭代方法姿态初始值，在计算机视觉领域有较多的应用。因此，学者开始研究对传统方法进行改进，文献[6]将二维DLT初值经解析后得到标定参数初值，再利用光束法平差予以精化，取得了很好的效果。计算机视觉领域对于相机姿态估计的文献也比较多，文献[7—8]提出了两种有效的线性解算姿态方法，其中文献[8]提出的EPnP算法得到了较高的评价，并在后期全景图像姿态估计上获得不断改进[9]。另外，还有学者将影像位姿参数求解转化为立体几何边角关系[10]。

本文从摄影测量学基本方程出发，提出一种基于Procrustes理论和基点组结合的影像姿态估计新方法，试验结果表明，通过该方法得到的姿态参数精度较改进的投影矩阵分解方法要高。

1 共线方程的矩阵表达

在摄影测量学研究中，采用欧几里得坐标表达物点和像点之间的关系，并且相关参数具有具体的物理意义，在相机经过检校并忽略影像畸变的情况下共线条件方程为

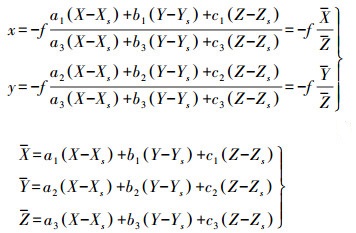(1)

式中，x、y为像点量测坐标；X、Y、Z为物点坐标；Xs、Ys、Zs为相机位置；a1—c3为姿态角(φ-ω-κ)构成的旋转矩阵元素；若将式(1) 转换为矩阵[11-13]，则可表示为

(2)

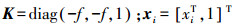
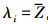
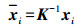
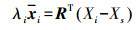式中，R为像空间辅助坐标系到地面摄影测量坐标系的旋转矩阵；为像点齐次坐标，xi为像点的欧氏坐标；Xi为同名物方点的欧氏坐标；λi为深度，。由于K已知，则，即像点坐标经过了规范化，则

(3)

为表示方便，下文表述中以xi代替xi。

2 本文方法步骤

在位姿估计研究中，关键是利用物方及像方同名点通过共线方程式(2) 估计式中的λi、R及Xs。由于这些参数耦合在一起，待求参数向量的显式表达式很难得到，因此所有参数解很难一次性解得，有必要对各个参数分别进行求解。

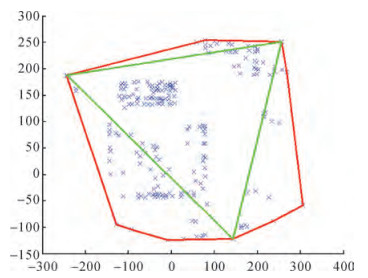
2.1 基点组选择

为求得各个待定参数，首先选择基点组，即选择分布合理、质量可靠的3个物点作为基点，所有物点坐标向量均可由基点坐标向量进行表达。由于参数估计的质量受到基点选择的直接影响，因此，在所有参与姿态估计的像点所构成的凸包中，选择3点构成面积最大的一组像点对应的物点作为基点。如图 1所示，×为所有的像点，黑线为像点的凸包络线，由其节点参与姿态估计，而灰色三角形顶点为选取的3个基点。

图 1 图像基点组选择
图选项
2.2 深度及平移向量的计算

{X1, X2, X3}为选择的基点组，由于基点不共线，则行列式|X1, X2, X3|≠0，令

(j=4, 5, …，N)，则式(3) 可转化为

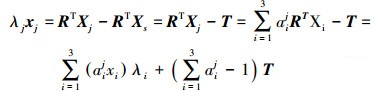(4)

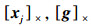
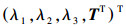
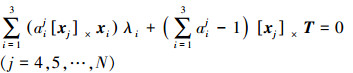式中，T = RTXs。对式(4) 两侧同乘为反对称矩阵。可以得到关于参数的齐次方程组

(5)

记式(5) 的最小二乘解为

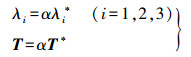(6)

式中，α>0为标量，将式(6) 代入式(3) 中，得

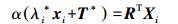(7)

由旋转矩阵的保范数特性知

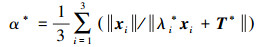(8)
2.3 旋转矩阵计算

由式(6) 和式(8) 可知，式(3) 转化为

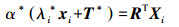(9)

或

式中，。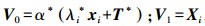

由此，问题转化为由V0和V1估计旋转矩阵R。这里直接采用Procrustes理论[14]计算三维相似变换模型，步骤如下：

2.3.1 计算幂等矩阵C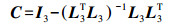
(10)

式中，I为单位阵；L为元素为1的列向量。

2.3.2 奇异值分解M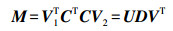
(11)

式中，D为单位阵；U和V为正交向量。

2.3.3 构建旋转矩阵R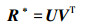
(12)
2.3.4 外参数分解

由旋转矩阵继而可得到图像外参数(角元素为φωκ转角系统)

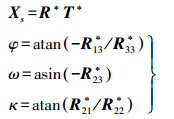(13)

需要特别指出，在估计过程中，位姿参数间的相关性及控制点的不合理分布(如共线共面或原点设置等)直接影响解的精度和稳定性，针对该情况本文采用物方坐标归一化预处理[15]，即Xi= WXi，W为相似变换矩阵。

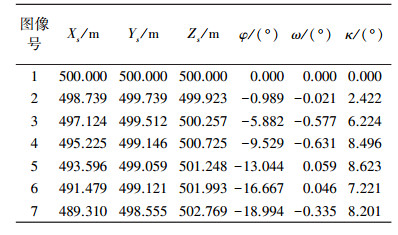
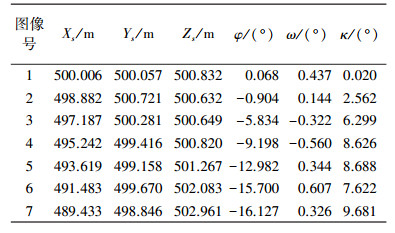
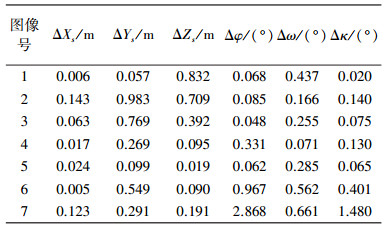
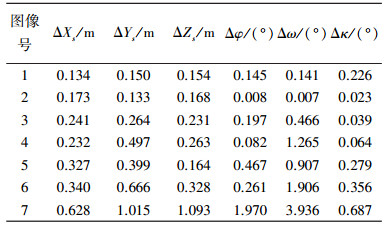
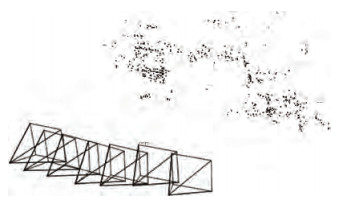
3 试验结果

试验中，选用稀疏光束法平差[16](SBA)中7幅近景图像数据，由于原数据尺度未知，为定量分析方法的有效性，首先对其进行尺度放大(1000倍)及原点平移(500 m)，使数据为米制，如图 2所示。选择所有数据中最大凸包点参与估计，每张像片参与估计的同名点数点见表 1，已知像点坐标、物方点坐标，外方位元素数据列于表 2。试验结果与已知位姿数据比较后，绝对误差分别见表 3、表 4。

图 2 7幅图像位姿及物方控制点分布情况
图选项
表 1 参与位姿估计的点数
表选项
表 2 已知图像外参数
表选项
表 3 本文方法估计后的图像外参数
表选项
表 4 本文方法估计后的图像外参数绝对误差
表选项

从表 4对比来看，本文方法最后得到的位置绝对误差最大值为0.983 m，基本在0.5 m内；姿态绝对误差最大值为2.868°，其余均在较小范围内，质量较好；相比改进的投影矩阵分解方法[9-10]，本文方法在姿态估计的精度上有了明显提高，结果见表 5。如果以此结果作为初值，进一步通过迭代精化，位姿参数精度会进一步提高。

表 5 奇异值分解方法得到的图像外参数绝对误差
表选项
4 结语

针对图像位姿估计问题，建立了一种分层估计位姿参数的方法，该方法通过选择分布质量较高的一组点作为基点，能有效提高图像姿态参数估计的质量。

(1) 建立了一种基于最大面积凸包的基点选择方法，该方法对于提高位姿参数估计质量具有重要意义。

(2) 由于DLT方法估计到的位姿参数精度较低，并且待估参数间具有很强的耦合性。为此，建立了分层最小二乘估计图像位姿方法，相比于直接对投影矩阵分解的方法，参数估计精度有很大提高，如果以此结果作为初值通过整体求解，位姿参数精度会进一步提高。

参考文献
[1] 张祖勋, 苏国中, 张剑清, 等. 基于序列影像的飞机姿态跟踪测量方法研究[J]. 武汉大学学报(信息科学版), 2004, 29(4): 287–291.
[2] 袁修孝, 余翔. 高分辨率卫星遥感影像姿态角系统误差检校[J]. 测绘学报, 2012, 41(3): 385–392.
[3] 王之卓. 摄影测量原理[M]. 北京: 测绘出版社, 1980.
[4] 冯文灏. 近景摄影测量——物体外形与运动状态的摄影法测定[M]. 武汉: 武汉大学出版社, 2002.
[5] 李德仁, 郑肇葆. 解析摄影测量学[M]. 北京: 测绘出版社, 1992.
[6] 张永军, 张祖勋, 张剑清. 利用二维DLT及光束法平差进行数字摄像机标定[J]. 武汉大学学报(信息科学版), 2002, 27(6): 566–571.
[7] FIORE P D. Efficient Linear Solution of Exterior Orientation[J]. IEEE Trans. Pattern Analysis and Machine Intelligence, 2001, 23(2): 140–148. DOI:10.1109/34.908965
[8] LEPETIT V, MORENO-NOGUER F, FUA P. EPnP:An Accurate O(n) Solution to the PnP Problem[J]. International Journal of Computer Vision, 2009, 81: 155–166. DOI:10.1007/s11263-008-0152-6
[9] 邓非, 吴幼丝, 胡玉雷, 等. 球形全景影像位姿估计的改进EPnP算法[J]. 测绘学报, 2016, 45(6): 677–684. DOI:10.11947/j.AGCS.2016.20150411
[10] 冯其强, 李广云, 黄桂平. 数字工业摄影测量中的单像空间后方交会[J]. 测绘通报, 2008(6): 4–6.
[11] 徐振亮, 闫利, 段伟, 等. 车载序列影像直接相对定向质量[J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(3): 321–325.
[12] 徐振亮, 李艳焕, 闫利. 单张大角度影像后方交会初值确定方法[J]. 辽宁工程技术大学学报(自然科学版), 2014, 33(7): 951–954.
[13] 徐振亮, 闫利. 轴角描述的光束法平差新方法[J]. 武汉大学学报(信息科学版), 2015, 40(7): 865–869.
[14] MAHBOUB V, SHARIFI M A. On Weighted Total Least-Squares with Linear and Quadratic Constraints[J]. Journal of Geodesy, 2013, 87(3): 279–286. DOI:10.1007/s00190-012-0598-8
[15] HARTLEY R, ZISSERMAN A. Multiple View Geometry in Computervision[M]. 2nd edition. Cambridge:Cambridge University Press, 2000.
[16] LOURAKIS M, ARGYROS A. The Design and Implementation of Ageneric Sparse Bundle Adjustment Software Package Based on the Levenberg-marquardt Algorithm[C]//Technical Report 340.[S.l.]:Institute of Computer Science-FORTH, 2004.
http://dx.doi.org/10.13474/j.cnki.11-2246.2017.0181
国家测绘地理信息局主管、中国地图出版社（测绘出版社）主办。
0

文章信息

李艳焕，徐振亮，邵良杉
LI Yanhuan, XU Zhenliang, SHAO Liangshan
一种新的影像位姿直接估计方法
A Novel Direct Estimation Method for Image Pose
测绘通报，2017(6)：17-20.
Bulletin of Surveying and Mapping, 2017(6): 17-20.
http://dx.doi.org/10.13474/j.cnki.11-2246.2017.0181

文章历史

收稿日期：2016-10-23
修回日期：2017-01-13

相关文章

工作空间