2. 长江水利委员会长江科学院, 湖北 武汉 430010;
3. 中国地质大学(北京), 北京 100083
2. Changjiang River Scientific Research Institute of Changjiang Water Resources Commission, Wuhan 430010, China;
3. China University of Geosciences (Beijing), Beijing 100083, China
大规模使用无人机进行遥感测量已经是航空测绘发展的一个重要趋势,总的来说,无人机遥感系统[1-2]具有运行成本低、反应速度快、人员安全性高等多种优点,从某种意义上讲,无人机已经是遥感数据获取的重要工具。近年来,随着技术的成熟发展,各种性能优异的无人机开始广泛地应用于军用战场侦察监视、民用资源调查等,随之而来的是大量具有高时效性、高精确度的地理影像数据;与此同时,各种具体应用已经不再是几张简单的图像信息就可以满足的了,人们需要从中获取更多的、更加详细的空间三维信息,这就需要研究人员加大无人机影像研究力度,以便更好更快地获取有效的空间三维地理信息。
在摄影测量[3]中,空间点需要在两张立体像对中找到同名点后进行交汇得到,而特征同名点的查找可以通过多种特征点检测算子得到,但是特征点检测算子进行匹配时整体效率低且缺乏有效的约束条件,也难以在匹配结果上进行进一步的精华校正。为了提高特征点匹配效率,减小匹配错误率,同时能有效进一步研究稠密匹配,在实际的无人机同名点匹配中,有必要预先对其进行核线影像[4]生成处理。与此同时,计算机视觉领域[5]近些年取得了一些突破性的研究成果,针对核线改正影像,计算机视觉领域采用了Graphic Cut图割[6]、belief propagation置信度传播[7-9]、联合区域优化[10]等算法,取得了良好的匹配结果,为稠密匹配提供了良好的理论基础,因此,有必要在核线同名点匹配方面引入计算机视觉稠密匹配的方法。
本文选取两张普通的含有重叠区域的无人机立体像对,对立体像对提取核线后进行核线重排生成核线影像,部分重叠区域如图 1所示,分辨率都为1000×1000像素;然后用尺度不变特性变换(scale invariant feature transform,SIFT)算子[11-13]和BP(belief propagation)算法[7-9]分别进行稀疏匹配与稠密匹配,对于获取的同名点,将其返回原始图像后结合投影矩阵可以进行同名点空间位置解算,最后两种方法都获取一组带颜色信息的空间点云。

|
| 图 1 核线立体像对 |
SIFT算子[11-13]是G.Lowe总结了当时已有的基于不变量技术的特征检测方法后提出的一种基于尺度空间、图像缩放、旋转甚至仿射变换保持不变形的图像局部特征描述算子。具体而言,SIFT算法是基于图像特征尺度选择的思想,SIFT算子首先建立图像的多尺度空间;然后在不同尺度下检测到同一个特征点,确定特征点位置的同时确定其所在尺度,以达到尺度抗缩放的目的;最后剔除一些对比度较低的点及边缘响应点,并提取旋转不变特征描述符,以达到抗仿射变换的目的。
在实际的处理过程中,SIFT算子处理能力较强,能快速获取少量同名点,若不加入核线约束、水平误差约束等条件,计算结果会出现不少错误匹配点。使用SIFT算子进行处理后,图 1中左片获取了4185个特征点,而右片得到了4103个特征点,在没有核线约束与水平误差约束的情况下,对左右影像的特征点进行匹配处理后可以得到420个匹配点。将同名匹配点两两间联立起来,其结果显示效果如图 2所示。

|
| 图 2 SIFT算子提取结果 |
从图 2可以看出,大部分正确匹配点都处于同一水平线上,但部分匹配点出现了较大的偏差,通过限定特征点的垂直误差阈值及最大视差范围,可以消除掉大部分的错误匹配点。若以图 2中两幅影像为例,限定同名点的匹配结果垂直误差为上下一个像素,水平视差为30个像素,处理可删除部分匹配点,最后可得到268对匹配点,结果如图 3所示。

|
| 图 3 核线约束下的SIFT算子特征点计算结果 |
从图 3可以看出,SIFT算子处理速度快,精度比较高,但是其处理效率低,对影像信息的利用率比较低。图 3中原始影像包含100万个像素,SIFT算子仅仅匹配了268对同名点,在这种情况下,若要获取更多的同名点,只能通过两种方法来实现:① 增加影像的数目。虽然单独的立体像对获取的同名点数目较少,但如果立体像对数目增加了,最终获取的同名点对数也会随之增加,在本次研究中,基于400余幅两两相邻的影像使用SIFT算子批次处理后最终获取了265 864对同名点,提取出了大范围区域的概要轮廓空间信息。② 对影像信息进行更深层次的挖掘。虽然增加影像的数目可以有效增加同名点的对数,但是对于小范围的地物而言同名点对数还是过少,这导致了地物三维重建时信息不足,因此在实际应用中有必要研究立体像对的稠密匹配技术,在立体像对中提取大量的同名点,从而有效提高影像的信息利用率。
2 基于BP算法[7-9]的稠密匹配BP算法是基于可尔可夫随机场(Markov random field,MRF)的一种最优化求解方法。假设每幅影像是一个规则排列的像素场,在计算机视觉领域中经常使用MRF来模拟像素场的像素排列方式与赋值情况,对于核线立体像对同名点匹配而言,参考影像上每个像素均会有多种候选值,将每一个像素的取值情况均转化为相应的MRF能量,然后联立所有的像素取值情况整体求解,按照某种最优化方法求解后就能得到像素场的整体最优解。
使用BP算法,以图 1中的两幅核线影像为试验对象,限定最大视差为30个像素,以右图为参考、左图为目标,可以计算出右图中每一个点与左图中同名点的水平距离差(即视差);随后把水平距离值乘以8就能得到一个灰度值,将每个像素的灰度值都求解出来,就能算出以右图为参考对象的视差图,如图 4所示。

|
| 图 4 视差空间(灰度值=同名点水平差异×8) |
可以看出,视差图与右核线图实际情况相符合,整体上包含了两层楼顶、地面背景的三层视差结构,4个屋顶的视差图都比较平整,可以看成一个整体,背景区域结算与实际区域也较符合,整体上也体现出了视差的真实排列情况,但是在视差图中左边缘不清晰,部分区域出现了整体性的结算错误,这也就给下一步的空间点坐标计算带来了误差。
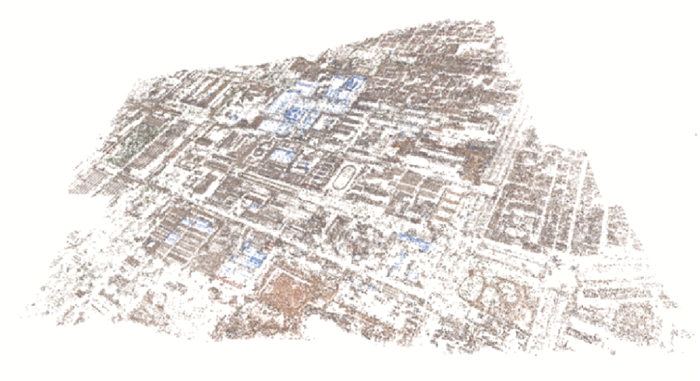
3 试验结果在核线影像上获取同名点后,可以将两个点返回立体像对,通过立体像对的两个摄像机矩阵就能直接求解出同名点的空间坐标,同时通过双线性插值方法也能得到同名点的颜色信息。在本文研究中使用SIFT算子来进行稀疏匹配时,处理了包含上述立体像对在内的5个航带的400余幅无人机影像,影像间隔约50 m,编写程序批次处理后获取了265 864个空间点,稀疏点云在Meshlab软件的显示效果如图 5所示。整个区域可以看出大致的空间结构,主要的地物框架都有所体现。
|
| 图 5 基于SIFT算子的稀疏匹配结果 |
使用BP算法进行稠密匹配时,以图 2中的核线立体像对为例可以计算出一个包含了大量匹配点的密集点云,对每一对同名点进行简单的RGB差异控制后能够获取约635 275个空间点,其空间效果如图 6所示。可以明显看出,地物的空间结构包含了6个独立的楼顶和相对完整的地表面, 而视差图中的错误部分也造成了空间点的计算错误,出现了不少缺失与空洞。

|
| 图 6 基于BP算法的稠密匹配结果 |
在试验中,两种方法都能够有效地获取同名点,根据相应的摄像机矩阵计算后都能够获取到有效的三维点云,具体而言,两种方法存在以下不同:
(1) 影像信息利用率不同,整体上而言,使用SIFT算子获取的同名点对数较少,而使用BP算法进行稠密匹配得到的同名点对数远远超过了SIFT算子的效果。图 2中包含了屋顶和四边形广场两种典型的空间地图结构,单幅核线影像包含100万个像素,其中6个屋顶由约30万个像素组成,垂直方向上分为两层,四边形广场由约19万个像素构成,使用SIFT算子和BP算法分别进行稀疏匹配和稠密匹配后的结果见表 1。
| 算法 | 整幅影像 | 屋顶 | 四边形广场 |
| 总像素/个 | 1 000 000 | 约280 000 | 约190 000 |
| SIFT算法同名点匹配对数/对 | 268 | 37 | 86 |
| BP算法同名点匹配对数/对 | 635 275 | 235 874 | 168 245 |
可以看到,使用BP算法后,从影像中获得的同名点对数远远超过了SIFT算法所得到的,SIFT算子所得到的结果对影像的利用率不到千分之一,而BP算法得到的结果对影像的利用率达到了63.5%。虽然BP算法的结果还存在许多误差匹配点,但是在庞大的匹配基数支持下,即使使用各种检验方法剔除了大量无匹配点,其结果信息利用率也会远远大于SIFT算子。
(2) 计算复杂度不同,SIFT算子进行处理时所耗费的时间远远少于BP算法。在SIFT算子进行处理的过程中,每张相片的像素都只会进行一次计算而不会进行迭代计算,以图 2为例,SIFT算子先处理左影像得到4185个特征点,随后处理右影像得到4103个特征点,在后面的计算中,SIFT算子进行匹配的时候只是在特征点间进行匹配而不会处理剩下的像素点;而上述像对在BP算法处理时,对于参考影像上的每一个像素点都会进行迭代处理,假设每个点的求解空间为30个像素,那么在计算时100万个像素点每个都会有30种求解候选值,每一个候选值的概率都会受上下左右4个方向上的传递消息的影响,每迭代一次,消息更新一次,每个候选值的概率也会随之更新,在这个过程中所耗费的计算资源远远大于SIFT算子计算处理方法,处理时间也大大超过了SIFT算子。
(3) 点云准确度不同,虽然SIFT算子处理得到的结果点较少,但其匹配点准确度要超过BP算法结果。SIFT算子在进行特征点计算时每一个特征点包含了128种信息,坐标计算可以达到亚像素级,这样每一对同名点在进行三维空间坐标计算时能够达到更好的精度;而BP算法在进行同名点计算时,受制于计算复杂度,每个像素点的求解区域只能达到像素级,这在后续的空间点坐标计算时产生了不利的影响。
(4) 适用范围不同,SIFT算法可以快速而有效地获取大范围的主要轮廓图,而BP算法能够获取到地物的详细空间信息。SIFT算法计算快速而准确,能够大批量处理影像,从而快速提取到大范围的主要空间信息;而BP算法在处理时会耗费大量的计算资源,虽然它能够获取到远远多于SIFT算子的空间点数,但是在处理相同多的影像时,BP算法耗时耗力,无法满足时效性的需求。
5 结论与展望(1) 无人机影像经过水平核线影像生成处理后能够有效减少空间同名点的搜索空间,在实际处理时给稀疏匹配与稠密匹配打下了良好的基础。
(2) SIFT特征算子在处理大范围的无人机影像数据时,可以准确有效地处理无人机影像数据,获取所在地区的简要三维轮廓信息,部分满足实际的需求。但是稀疏匹配中影像的信息利用率过低,在本次研究中使用了400余幅千万像素的影像,最后只获取了不足30万个特征点,虽然计算出来的三维空间点位置信息较为精确,但是点云分布极为稀疏,导致后续的三维物体重建信息量不足。
(3) BP算法在处理小范围的空间地物时能够最大限度地挖掘出影像的信息,在本次试验中,BP算法获取了远多于SIFT算法的空间点数,虽然匹配结果中存在较多的错误匹配点,且具有匹配点精度不够的缺点,但是结果点云已经能够较好地反映出地物的空间结构情况。在后续的研究中需要改进视差图,并且研究能够更好检验与消除错误匹配点方法。
(4) 在实际应用中,SIFT算法能够快速获取大范围的空间信息,而BP算法能够很好地计算出典型地物的空间点云图,两者可以互补,从而在生产研究中得到更好的空间数据产品。
| [1] | 韩杰, 王争. 无人机遥感国土资源快速监察系统关键技术研究[J]. 测绘通报, 2008(2): 4–15. |
| [2] | 崔红霞, 林宗坚, 孙杰. 大重叠度无人机遥感影像的三维建模方法研究[J]. 测绘科学, 2005, 30(2): 37–39. |
| [3] | 张祖勋, 张剑清. 数字摄影测量[M]. 武汉: 武汉测绘科技大学出版社, 1996. |
| [4] | 张祖勋. 数字影像定位及核线排列[J]. 武汉测绘学院学报, 1983(1): 12–14. |
| [5] | SCHARSTEIN D, SZELISKI R. A Taxonomy and Evaluation of Dense Two-frame Stereo Correspondence Algorithms[J]. International Journal of Computer Vision, 2002, 47(1-3): 7–42. |
| [6] | BLEYER M, GELAUTZ M. Graph Cut Based Stereo Matching Using Image Segmentation with Symmetrical Treatment of Occlusions[J]. Signal Processing:Image Communication, 2007, 22(2): 127–143. DOI:10.1016/j.image.2006.11.012 |
| [7] | SUN J, ZHENG N N, SHUM H Y. Stereo Matching Using Belief Propagation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(7): 787–800. DOI:10.1109/TPAMI.2003.1206509 |
| [8] | FELZENSZWALB P F, HUTTENLOCHER D P. Efficient Belief Propagation for Early Vision[J]. International Journal of Computer Vision, 2006, 70(1): 41–54. DOI:10.1007/s11263-006-7899-4 |
| [9] | YANG Q, WANG L, YANG R, et al. Stereo Matching with Color-weighted Correlation, Hierarchical Belief Propagation, and Occlusion Handling[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(3): 492–504. DOI:10.1109/TPAMI.2008.99 |
| [10] | WANG Z F, ZHENG Z G. A Region Based Stereo Matching Algorithm Using Cooperative Optimization[C]//IEEE Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE, 2008:1-8. |
| [11] | LOWE D G. Object Recognition from Local Scale-invariant Features[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision.[S.l.]:IEEE, 1999:1150-1157. |
| [12] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [13] | 王国美, 陈孝威. SIFT算法研究[J]. 盐城工学院学报(自然科学版), 2007, 20(2): 1–5. |


