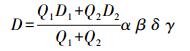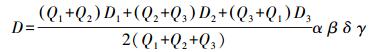2. 北京市测绘设计研究院, 北京 100038;
3. 城市空间信息工程北京市重点实验室, 北京 100038
2. Beijing Institute of Survey and Mapping, Beijing 100038, China;
3. Beijing Key Laboratory of Urban Spatial Information Engineering, Beijing 100038, China
室内定位技术填补了GNSS技术所不能涉及的领域,在一些特定的场合,如大型的建筑物内、车站、购物中心、地下停车场等室内环境,室内定位技术在应用上被寄予更多的期望,它不但能进行定位和导航,而且在此基础上可以开发出更多的增值服务。室内定位技术的应用场景主要包括:
(1) 安全措施与防范。在车站和商业购物中心内,如果发生了难以抗拒的突发事件,如火灾、地震、洪水、暴恐袭击等,可以利用室内定位与导航技术,准确、快速地找到被困者并施救。
(2) 大型建构筑物内的定位与导航。当进入一个陌生的环境,想要找到某一个特定地点,如厕所、出口、地下停车场或某一个商铺,利用室内定位技术可以完成自身定位,并且可以实现导航指引。
(3) 消息的推送与广告投放。通过室内定位技术,可以收集个人的行进轨迹,通过其轨迹的分布和停留点的位置,可以精确地将个人感兴趣的信息和广告进行推送[1]。
室内定位技术的应用极其广泛,其商业价值十分可观,因此,对于室内定位技术的研究具有很高的价值和意义。
室内定位技术的方法有很多种,包括无线网络技术、蓝牙、红外、RFID和行人航迹推算PDR(pedestrian dead reckoning)等[2]。不同的定位方法具有不同的定位原理,有基于传播时间的定位法、基于电波传播模型的定位法、位置指纹定位法等。不同的定位环境需要采用不同的定位方法。基于WiFi信号的三角形定位法定位精度高,建设费用低,适用于人群密集的大型车站和地下停车场等环境;基于传播时间的定位法需要很高的时间测量精度,对设备仪器的硬件条件很高,受外界的环境因素干扰较大,适合比较空旷的室内环境下定位;基于位置指纹定位法定位精度高,适用的范围广,但是建设成本比较高,需要建立大量的数据库作为定位的前提条件,花费较大,前期投入高。
1 基于WiFi信号的三角形定位法基于WiFi信号的三角形定位法是基于WiFi热点信号强度来进行定位的, 相比于其他的定位方法,三角形定位法的建设成本低,运行维护的投入小,适用的环境广泛,计算模型比较简单,受外界因素的干扰较小[3]。
1.1 三角形定位法的测距原理在进行测距阶段的过程中,首先要确定至少3个WiFi热点的坐标信息,通过移动接收端接收到的信号强度,按照式(1) 中无线电波传输过程中损耗模型公式计算出待定位点距离每一个WiFi热点的距离[4]
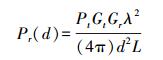 (1)
(1) 式中,Pr(d)表示移动接收终端接收到的信号功率;Pt为WiFi热点AP的传输功率;Gt为信号发射端的增益;Gr为移动接收端的增益;λ为电波的波长;L为损耗系数;d为WiFi热点AP和移动终端的距离。可以看出,式(1) 中只有距离d是未知的,可根据公式中的各个已知量来计算出移动终端距离WiFi热点的距离d,根据已知的3个WiFi热点的坐标,就可以利用三角定位法来计算出具体位置了[5]。
在进行定位的过程中,无线电波的信号会随着定位距离的增加而减弱,根据式(1) 中的等式可以看出它们之间的关系。但是,在实际定位过程中,由于定位的条件和环境都很复杂,电磁波在传输的过程中出现损耗,也可能出现电磁波信号的衰落,由于受到种种因素的影响。在一般的环境下,通常采用式(2) 的定位模型来代替式(1) 的电磁波传输损耗模型
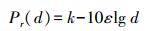 (2)
(2) 式中,ε表示非自由空间的消耗系数;d代表信号接收端与发射端的距离;k可以用式(3) 的常数表示
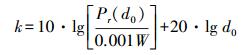 (3)
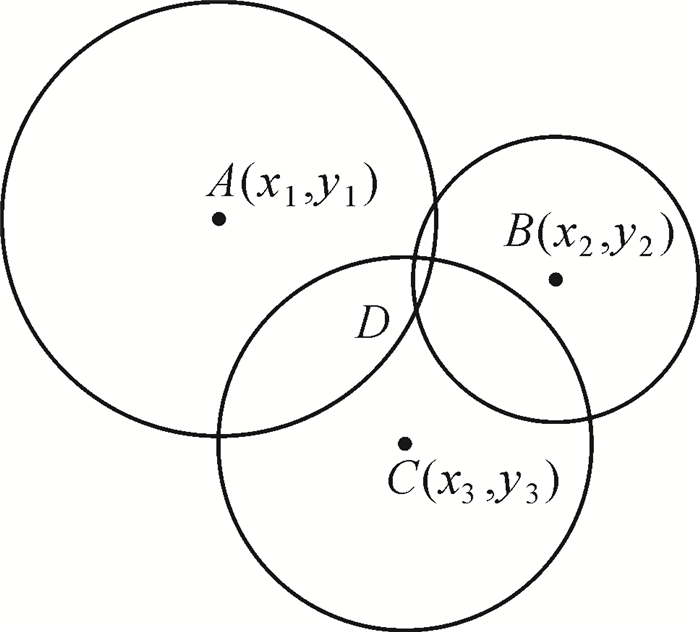
(3) 图 1中,A、B、C 3个点为已知坐标的WiFi热点,AD、CD、BD3条边分别是定位待定点到3个WiFi信号发射端的距离。分别以3个WiFi信号发射端作为圆心, AD、BD、CD3条边为半径作圆,使得这3个圆相交于一点,该点D的坐标即为所需要的待定点位坐标[6]。
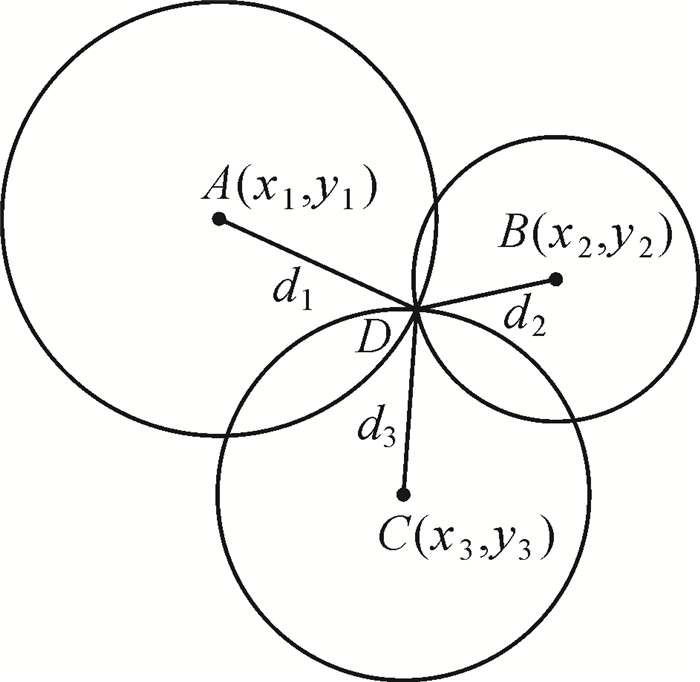
|
| 图 1 定位示意图 |
将待定点位D的坐标设为(x, y),A、B、C 3个已知WiFi热点的坐标分别为(x1, y1)、(x2, y2)、(x3, y3),通过式(1) 计算出3个已知WiFi热点到待定点D的距离分别为d1、d2、d3,通过以下方程组来确定D的位置(x, y)
 (4)
(4) 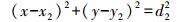 (5)
(5) 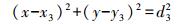 (6)
(6) 通过求解线性方程式(7),得出目标点位D的位置
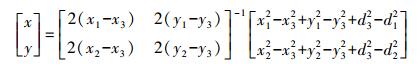 (7)
(7) 在理想的条件下,根据以上的方程组来确定D的位置(x, y)。但是在现实的定位过程中,会受到外界环境因素的干扰和影响,在计算待定点位D到3个已知WiFi热点的距离过程中,有可能出现3个圆不相交于一点的情况,那么在利用方程组求解的过程中就会出现无解的状态。图 2和图 3是两个典型的无解状态[7]。

|
| 图 2 方程组无解情况1 |
|
| 图 3 方程组无解情况2 |
为了解决这两个无解的状态,构造一个新的算法模型:首先根据式(4) 和式(5) 得到圆A与圆B的两个交点(xab1, yab1)和(xab2, yab2),根据式(4) 和式(6) 求解圆A与圆C的交点(xac1, yac1)和(xac2, yac2),根据式(5) 和式(6) 计算圆B与圆C的交点(xbc1, ybc1)和(xbc2, ybc2)。然后将圆A与圆C的交点(xac1, yac1)和(xac2, yac2)代入x-x22+y-y22中, 找出距离圆B圆心较近的点(xac, yac)。同理可求(xab, yab)和(xbc, ybc)。根据计算,可以得出待定位坐标的近似坐标[8]
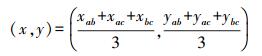 (8)
(8) 根据以上公式可以看出,在室内定位过程中,对定位精度影响较大的是电波在空气中的传播模型及3个WiFi热点的坐标位置。当在不同的环境下进行定位时,影响因素各不相同,因此要想达到更精准的定位精度,需要建立一个更加准确和周全的算法模型, 将环境影响因素和WiFi热点坐标信息进行加权去噪处理,称之为加权去噪模型。
2 加权去噪模型 2.1 三角形定位法的影响因素在进行室内定位的过程中,由于受外界条件的影响和各种因素的干扰,定位的精度会随之产生不同的变化,主要的影响因素如下[9]:
(1) 不同的障碍物对WiFi信号强度的影响。在WiFi信号的传播过程中,会随着距离的增加而减弱,遇到不同的障碍物会对信号的强度产生很大的影响,包括墙壁、家具、装饰材料等。这些物体可能对信号产生反射或吸收,如果将这些影响因素代入公式计算,就会对定位精度产生很大影响。将障碍物对信号的影响改正称为α。
(2) WiFi信号传播的多路径效应。在WiFi信号传播过程中,由于热点发射器发出的信号是发散的,从信号发射到接收的过程中,遇到不同的障碍物,所产生的反射和散射影响就会不同,会造成信号在传播过程中产生多个路径,在不同的传播路径中,到达的时间或相位就会不同,降低定位精度[10]。将多路径对信号的影响改正称为β,如图 4所示。
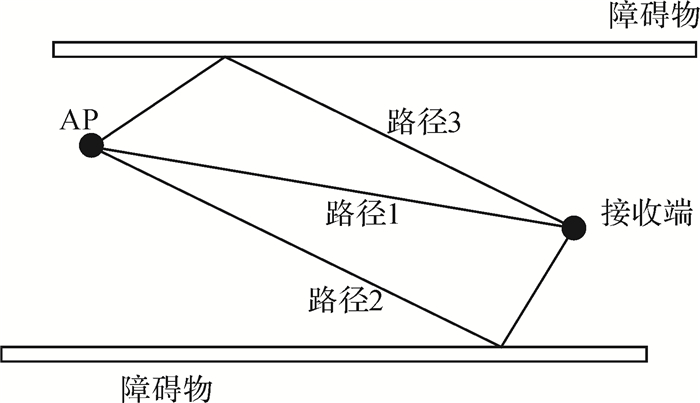
|
| 图 4 传播示意图 |
(3) 定位区域的大小对信号的影响。由于传播信号在传播过程中强度不断递减,如果定位的区域过大,在信号到达接收端时可能就会出现信号很弱甚至没有的情况[11]。将信号递减的影响改正称为δ。
(4) 其他信号的干扰。在复杂的环境中,可能还伴随着不同的信号在空气中传播,如手机、电视、电磁炉或微波炉的使用,这些信号都会对WiFi信号强度产生影响[12]。将其他因素的影响改正称为γ。
如何消除或减弱这些噪音对信号的影响,以便达到精度最高的定位精度,是需要解决的问题。
2.2 加权去噪模型的建立由于在室内WiFi信号的传播受到多种因素的干扰,信号强度的波动很大,需要将接收到的带有噪声的信号进行消除[13]。笔者采用加权的方法对WiFi信号进行去噪处理。
首先,要收集接收端的信号强度并与数据库的信号进行特征对比,选取距离热点比较近的接收端坐标为目标位置[14]。由于WiFi信号在传播的过程中有较大的波动,不会平稳地传输到各个收集端,因此在选取WiFi信号强度的过程中,不能将接收到的信号一一记录,需要进行试验,并且推算出每个信号接收端在接收过程中的变化区间,只有符合该区间内的信号强度,才能进行收集[15]。
在对收集信号进行特征匹配前,首先必须建立一个特征数据库,数据库的内容包括位置代码、点位距离热点的距离、WiFi信号强度和WiFi信号强度变化区间。位置代码是每一个信号接收端的唯一代码,利用这个代码区分每一个接收点;点位距离热点的距离是记录每一个接收点的位置距离WiFi信号热点的距离;WiFi信号强度指的是在该接收点上收集到的有意义的信号强度的平均数;WiFi信号强度变化区间指的是WiFi信号强度波动的半径,WiFi信号强度加上或减去这个值,就可以得出此处信号强度的波峰、波谷值及变化区间。
根据数据库中的WiFi信号强度和WiFi信号强度变化区间,利用这两个特征值对接收的位置进行判断。通过即时接收的信号与数据库中的特征值进行匹配,完成定位。笔者将收集到的信号来源和强度进行记录(AP1,STRONG1)、(AP2,STRONG2)、…、(APn,STRONGn),将记录的信息与数据库中的信息进行对比,采纳符合变化区间内的数值,并将该点位的权值加1。选取权值最大值Qmax的点位作为参考,将各个点的权值与权值最大值Qmax的差值在Δ以内的点位作为预设点位。Δ的值会随着不同的区域和位置而发生变化,在人流比较多的车站和商场,Δ的值就会比较大,Qmax-QP < Δ,Qp为第n个权值。
如果只得到一个预设点位,那么就可以认为该点位与数据库中的点位重合,数据库中的点位即为该点位。
如果得到的预设点位不止一个,那么先按照权值进行排列P1(Q1,D1), P2(Q2,D2), …,Pn(Qn,Dn), D为该点到WiFi信号热点的距离,Q为该点的权值。然后可以利用式(9) 计算得到WiFi信号热点的距离
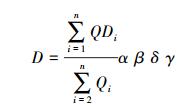 (9)
(9) 当预设点为两个时,套用式(9)
当预设点为3个时,套用式(9)
式中,α为障碍物对信号的影响改正;β为多路径效应对信号的影响改正;δ为信号递减的影响改正称;γ为其他因素的影响改正称。
利用以上模型可以得出该预设点位距离某一个热点信号的距离,通过加权配赋之后的距离值,会大大削弱噪声的影响,再利用三角形定位法计算该点坐标,可大大提高该点的定位精度。
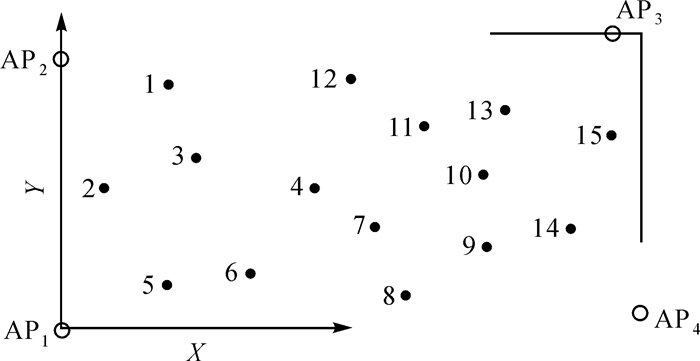
3 试验测试与分析 3.1 试验测试为了验证加权去噪模型的定位精度,开展定量试验测试。试验地点选定为某单位的室内定位检测场,测试环境为一个20 m×15 m室内场所,WiFi信号热点为4个,将AP1作为原点,建立坐标系。在本次试验中选择定位次数为15次,每一次定位都记录下实际的坐标,并且记录下每一次的定位结果。在试验前期,通过多次测试,收集了在试验过程中所需要的数据库,并且通过多次试验,得出了在试验过程中所需要的改正数α、β、δ、γ的数值。如图 5所示。
|
| 图 5 试验示意图 |
为了保障试验的准确性,在试验区域内平均选取了15个试验点,点位覆盖了整个试验区,为试验的准确性提供保障。试验结果如图 6所示。

|
| 图 6 结果对比 |
从结果对比图上可以看出,在相对空旷的室内检测场,经过加权减噪模型计算后的定位精度明显好于未经过改正的定位结果。在15个试验数据中,改正后的平均点位误差为0.80 m,超过1 m的点位误差共有4个,定位精度在1 m以下的有11个,占总比例的73.33%,最大的点位误差为1.35 m,最小的点位误差为0.46 m。没有经过加权减噪模型计算的点位的平均点位误差为1.22 m,超过1 m的点位误差共有10个,定位精度在1 m及以下的有5个,占总比例的33.33%,最大的点位误差为1.77 m,最小的点位误差为0.79 m。
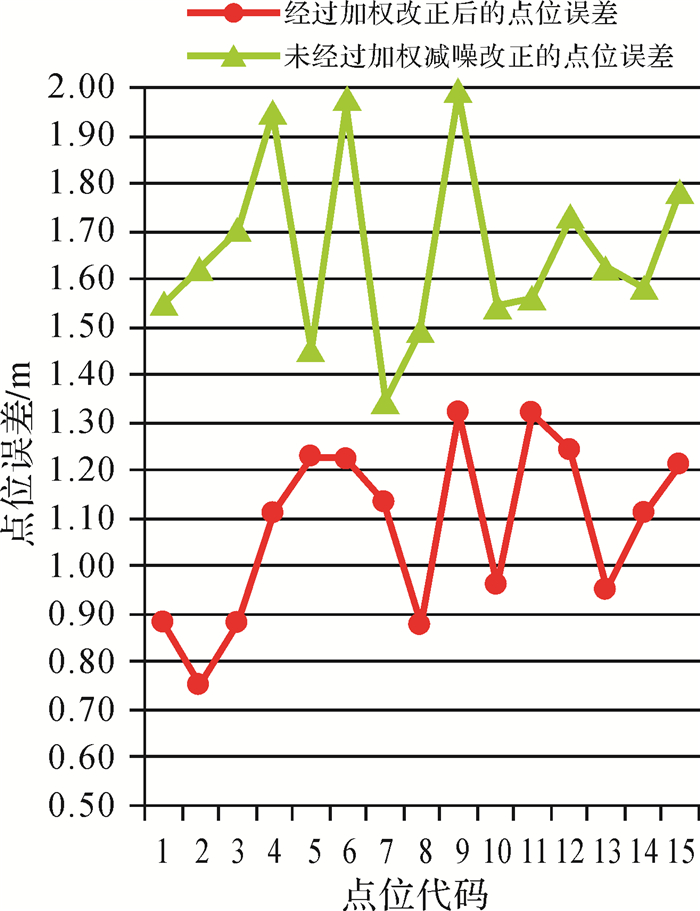
为了更好地检定加权减噪模型的稳定性,在相同的地点,增加定位区域内的环境因素,即在定位区域内,增加了携带手机的密集人员的流动,以及电脑、铁皮柜、电子设备等干扰因素,在其他条件不变的情况下进行试验,定位数据结果如图 7所示。
|
| 图 7 结果对比 |
从图 6、图 7可以看出,在这15个试验数据中,改正后的平均点位误差为1.08 m,没有经过加权减噪模型计算的点位的平均点位误差为1.66 m。
3.2 试验数据分析从上述试验结果可以看出,加权减噪模型在定位过程中提高了定位精度,不论是在空旷的条件下,还是在受到人员和电子设备干扰的情况下,加权减噪模型都起到了一定的作用,大大提升了定位的精度。除此之外,通过试验数据还可以看出,在复杂的条件下,加权减噪模型计算后的平均点位误差,比在空旷条件下的平均点位误差只增加了0.28 m,而没有经过加权减噪模型计算的那一组数据则增加了0.44 m。因此,加权减噪模型在抗干扰效果上稳定性更高。
4 结语加权去噪模型通过加权剔除了噪点,提升了定位的精度。无论是普通环境,还是在复杂的条件下,加权去噪模型的稳定性都得到了验证。随着社会的发展,室内定位的需求也会随之增加,定位的精度也会越来越高,应用的范围将会越来越广阔。
| [1] | 陈丽娜. WLAN位置指纹室内定位关键技术研究[D]. 上海: 华东师范大学, 2014. |
| [2] | 陈淼. 基于信号强度的WLAN室内定位跟踪系统研究[D]. 武汉: 武汉大学, 2012. |
| [3] | 李菁. 可见光室内定位技术研究[D]. 北京: 北京邮电大学, 2015. |
| [4] | 李魏峰. 基于RFID的室内定位技术研究[D]. 上海: 上海交通大学, 2010. |
| [5] | 刘春燕, 王坚. 基于几何聚类指纹库的约束KNN室内定位模型[J]. 武汉大学学报(信息科学版), 2014, 39(11): 1287–92. |
| [6] | 刘洺辛, 孙建利. 基于能效的WLAN室内定位系统模型设计与实现[J]. 仪器仪表学报, 2014, 35(5): 1169–1178. |
| [7] | 石欣, 印爱民, 陈曦. 基于RSSI的多维标度室内定位算法[J]. 仪器仪表学报, 2014, 35(2): 261–268. |
| [8] | 徐伟. 基于Android手机的室内定位技术研究与实现[D]. 武汉: 华中师范大学, 2014. |
| [9] | 颜俊杰. 基于WIFI的室内定位技术研究[D]. 广州: 华南理工大学, 2013. |
| [10] | 张宴龙. 室内定位关键技术研究[D]. 合肥: 中国科学技术大学, 2014. |
| [11] | REN Z, WANG G, CHEN Q, et al. Modelling and Simulation of Rayleigh Fading, Path Loss, and Shadowing Fading for Wireless Mobile Networks[J]. Simulation Modelling Practice and Theory, 2011, 19(2): 626–637. DOI:10.1016/j.simpat.2010.10.001 |
| [12] | YANG Y, ZHAO Y, KYAS M. RBGF:Recursively Bounded Grid-based Filter for Indoor Position Tracking Using Wireless Networks[J]. IEEE Communications Letters, 2014, 18(7): 1234–1237. DOI:10.1109/LCOMM.2014.2315632 |
| [13] | CASAS R, CUARTIELLES D. Hidden Issues in Deploying an Indoor Location System[J]. IEEE Pervasive Computing, 2007, 6(2): 62–69. DOI:10.1109/MPRV.2007.33 |
| [14] | VILASECA D I, GIRIBET J I.Indoor Navigation Using WiFi Signals[C]//2013 Fourth Argentine Symposium and Conference on Embedded Systems(SASE/CASE).[S.l.]:IEEE, 2013:1-6. |
| [15] | SARKAR T K, JI Z, KIM K, et al. A Survey of Various Propagation Models for Mobile Communication[J]. IEEE Antennas and Propagation Magazine, 2003, 45(3): 51–82. DOI:10.1109/MAP.2003.1232163 |