2. 同济大学测绘与地理信息学院, 上海 200092;
3. 武汉大学GNSS中心, 湖北 武汉 430079
2. College of Surveying and GEO-Informatics, Tongji University, Shanghai 200092, China;
3. GNSS Center of Wuhan University, Wuhan 430079, China
高精度GPS测量中,天线相位中心的偏差和天线相位中心变化是一项重要的误差源,其对高程分量的影响最为显著[1]。自1996年6月30日起,IGS的各数据分析中心开始利用相对相位中心的改正模型来改正这一误差项。相对相位中心改正的前提是假定参考天线(AOAD/M_T型天线)的PCV为0。但实际上AOAD/M_T型天线的PCV并不为0,再加上低高度角时通过相对校验方式得到的天线的PCV值所受到的多径影响将显著增加等一系列缺点[2],2006年11月后,IGS提供的天线产品均基于绝对相位中心改正模型的结果。此外,绝对天线相位中心改正模型除了考虑接收机天线相位中心的改正外,还给出了GPS卫星的天线相位中心的改正,以减小基于长基线测定的GPS全球参考框架与使用其他观测技术(VLBI和SLR)得到的结果间的尺度误差[3-8]。
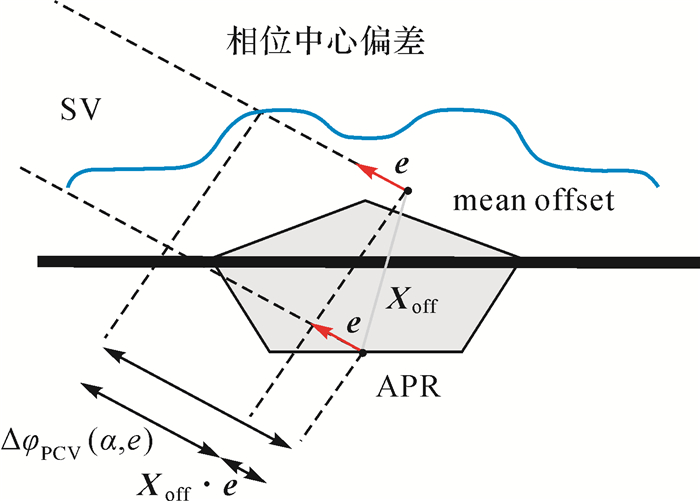
1 接收机天线相位中心改正对接收机而言,天线信号的相位中心不是固定的,而是随着卫星信号的入射方向变化的。天线瞬时相位中心偏差主要依赖于卫星的高度角和方位角。接收机天线类型决定了天线接收到的不同方向卫星信号相位中心的坐标。平均相位中心是不同方向卫星信号相位中心的加权平均值。平均相位中心和天线参考点所形成的向量即为天线相位中心偏差(PCO)。如图 1所示,天线相位中心偏差为Xoff。第2个接收机天线误差项为该接收机对卫星信号的瞬时相位中心和平均相位中心的偏差(PCV),该偏差为卫星高度角e和方位角α的函数[4],表示为ΔφPCV(α,e)。
|
| 图 1 接收机天线改正模型 |
由图 1可知,接收机对于高度角为e、方位角为α的卫星的相位观测值的接收机天线改正项为Δεφ(α,e),其计算公式如下
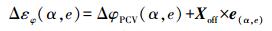 (1)
(1) 式中,e(α,e)为观测方向单位向量。
2 卫星天线相位中心改正卫星天线相位中心偏差(PCO)和天线相位中心变化(PCV)通常是在星固系下定义的。
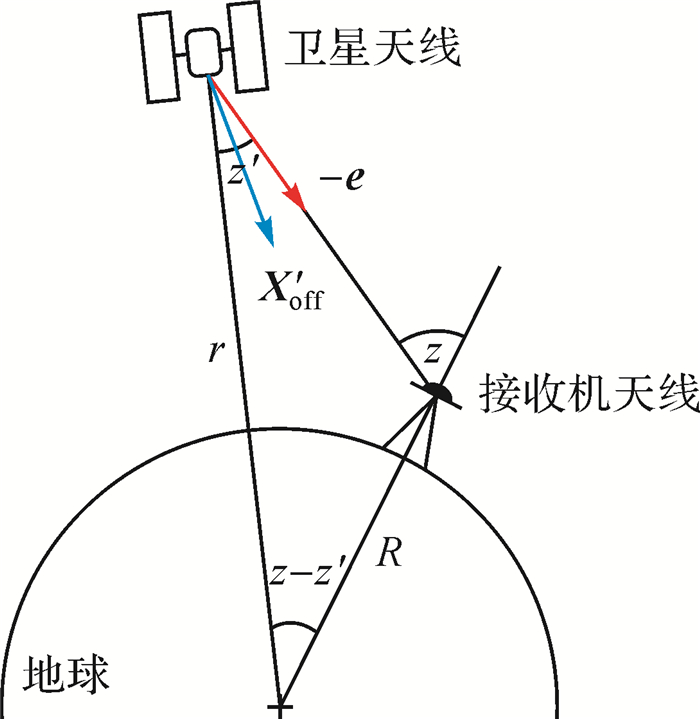
如图 2所示,在假设PCV仅与低点角(星固系Z轴与星地连线方向间的夹角)相关的条件下,由卫星天线PCO和PCV所引起的测站至卫星间距离观测值改正Δεφ′(z′),可表示为
|
| 图 2 卫星天线改正模型 |
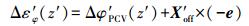 (2)
(2) 式中,z′为低点角,其计算公式如下
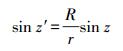 (3)
(3) 式中,R为地球半径;r为卫星到地心距离;z为测站卫星高度角的余角。Δφ′PCV(z′)表示低点角为z′时卫星天线PCV,X′off表示卫星天线PCO,-e表示星固系下卫星至接收机方向的单位向量[3]。
3 算例分析在基线长度较短(小于50 km)时,基线两端点GPS接收机对同一共视卫星的高度角和方位角基本一致,在形成站间单差观测值时,卫星天线的PCO和PCV改正将会被抵消掉。因此,本文主要选取长基线(100~1000 km)和超长基线(大于1000 km)来进行相关分析。
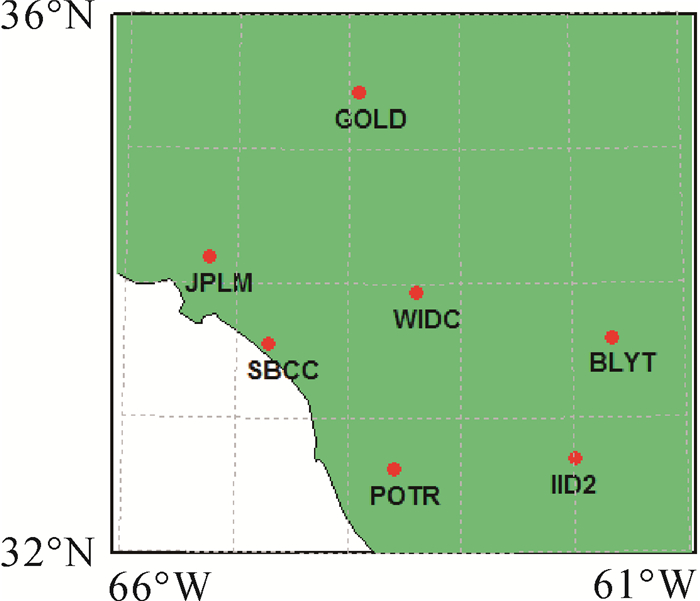
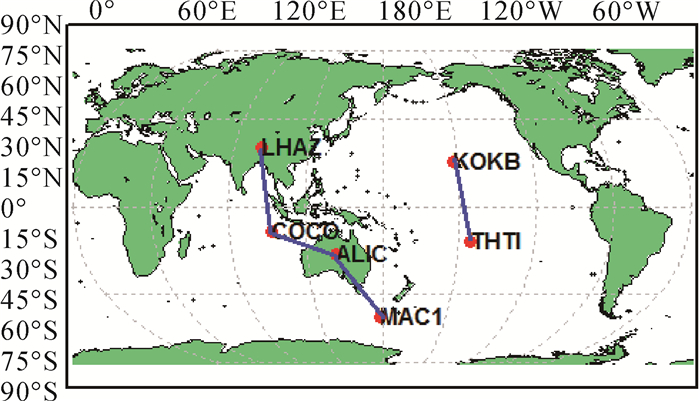
选取美国南加州的7个IGS观测站来组成长基线(测站分布如图 3所示),选取亚太地区的6个IGS观测站来组成超长基线,剔除部分长度超过5000 km的基线,最后形成的观测基线如图 4所示。取2016年年积日159—165的一周观测数据进行高精度基线解算[9-11]。
|
| 图 3 测站南加州分布 |
|
| 图 4 亚太地区测站分布 |
测站天线PCO改正的计算公式如下
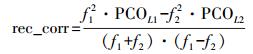 (4)
(4) 式中,rec_corr为测站地平坐标系中由测站接收机天线PCO引起的测站坐标改正量向量;f1表示L1频率;f2表示L2频率;PCOL1、PCOL2分别表示接收机天线L1、L2频率上的PCO。由测站天线PCO可得到测站天线PCO对测站坐标的改正量[12-16],见表 1。
| mm | |||||||||||||
| 测站 | BLYT | GOLD | IID2 | JPLM | POTR | SBCC | WIDC | ALIC | COCO | KOKB | LHAZ | MAC1 | THTI |
| N | 1.6 | 1.6 | 2 | 1.6 | 1.4 | 2 | 2.7 | 0.8 | 1.6 | 1.6 | 2.1 | 1.6 | 2.6 |
| E | 0 | 0 | -0.1 | 0 | 0.7 | -0.1 | -1.8 | 1.1 | 0 | 0 | 2.2 | 0 | -1.2 |
| U | 47.8 | 47.8 | 45 | 47.8 | 37.5 | 45 | 80.7 | 166.4 | 47.8 | 47.8 | 168.3 | 47.8 | 46.5 |
由表 1可知,在忽略N、E方向的测站坐标改正量的情况下,长基线BLYT、GOLD、IID2、JPLM、POTR、SBCC测站U方向坐标改正量均在35~50 mm之间,而WIDC测站U方向坐标改正量为80.7 mm;超长基线ALIC、LHAZ测站U方向坐标改正量在165~170 mm之间,COCO、KOKB、MAC1、THTI测站U方向坐标改正量在47 mm左右。将对卫星天线PCO、PCV和接收机天线PCO、PCV进行改正的基线解算结果与对卫星天线PCO、PCV和接收机天线PCV进行改正的基线解算结果作差,其结果见表 2。
| m | ||||||||||||
| 测站1 | 测站2 | ΔX | ΔY | ΔZ | ΔL | |||||||
| 平均 | 标准差 | 平均 | 标准差 | 平均 | 标准差 | 平均 | 标准差 | |||||
| BLYT | SBCC | 0.001 1 | 0.000 36 | -0.003 2 | 0.000 28 | 0.001 2 | 0.000 17 | -0.002 5 | -0.002 4 | |||
| BLYT | WIDC | 0.014 7 | 0.000 15 | 0.022 4 | 0.000 37 | -0.019 5 | 0.000 12 | -0.003 7 | -0.003 9 | |||
| GOLD | SBCC | -0.000 1 | 0.000 29 | -0.001 6 | 0.000 05 | 0.002 8 | 0.000 07 | -0.001 6 | -0.001 6 | |||
| GOLD | WIDC | 0.013 5 | 0.000 05 | 0.024 0 | 0.000 16 | -0.018 0 | 0.000 06 | -0.000 8 | -0.000 4 | |||
| BLYT | IID2 | -0.000 5 | 0.000 11 | -0.001 9 | 0.000 27 | 0.001 8 | 0.000 21 | -0.000 6 | 0.000 05 | |||
| POTR | WIDC | 0.017 4 | 0.000 05 | 0.029 8 | 0.000 19 | -0.026 1 | 0.000 08 | -0.002 3 | -0.002 6 | |||
| SBCC | WIDC | 0.013 5 | 0.000 25 | 0.025 6 | 0.000 17 | -0.020 8 | 0.000 09 | -0.000 2 | -0.000 1 | |||
| ALIC | COCO | -0.101 1 | 0.001 59 | 0.054 0 | 0.004 45 | -0.055 6 | 0.000 88 | -0.073 0 | 0.001 94 | |||
| ALIC | MAC1 | -0.078 9 | 0.000 64 | 0.101 0 | 0.001 36 | -0.025 0 | 0.001 14 | -0.068 9 | 0.001 63 | |||
| COCO | LHAZ | 0.003 2 | 0.007 80 | -0.043 7 | 0.010 90 | -0.077 9 | 0.004 10 | -0.069 7 | 0.003 24 | |||
| KOKB | THTI | 0.007 5 | 0.011 96 | 0.009 9 | 0.004 73 | 0.033 6 | 0.003 10 | -0.034 4 | 0.003 28 | |||
由表 2可知,ΔX、ΔY、ΔZ、ΔL的标准差对于长基线均小于0.4 mm,对于超长基线均在毫米级,少数几个达到厘米级但小于2 cm,说明连续单天解基线各分量差值非常稳定,可由ΔX、ΔY、ΔZ、ΔL多天的均值来分析差值的性质。测站天线PCO对长基线各分量的影响能达到厘米级,对超长基线各分量的影响能达到十几厘米。如果构成基线的两测站U方向坐标改正量相近,则基线各分量的偏差较小,长基线中的BLYT—SBCC、GOLD—SBCC、BLYT—IID2基线各分量偏差均小于3.2 mm。两测站U方向坐标改正量相差较大时,如POTR—WIDC各分量偏差可达3 cm;超长基线中的KOKB—THTI基线各分量偏差均小于3.3 cm,两测站U方向坐标改正量相差较大时,如COCO—LHAZ各分量偏差可达11 cm。
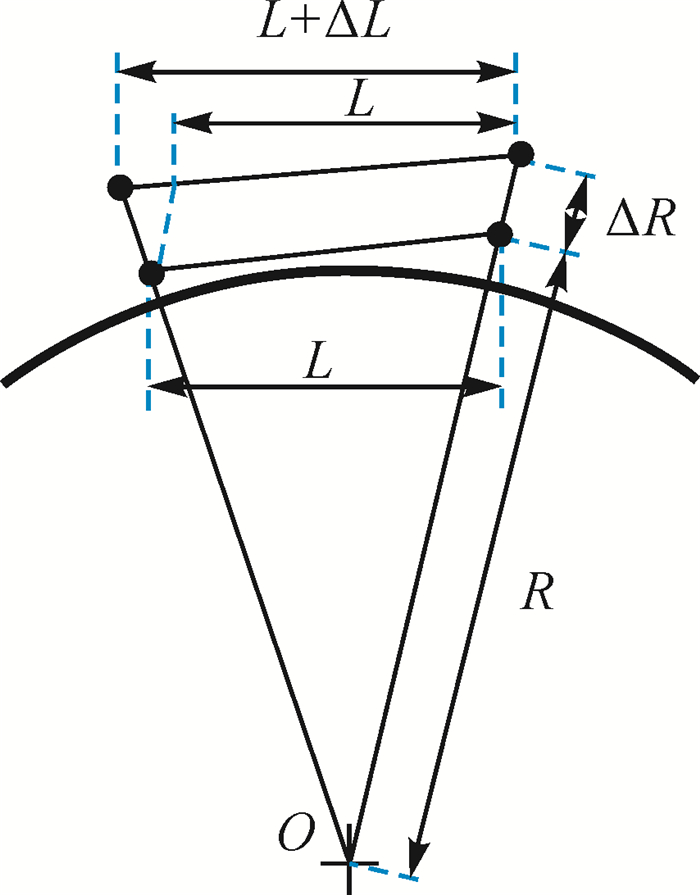
此外,表 2中ΔL均为负,说明未改正测站PCO基线长度会系统性地增加。在基线的两测站U方向坐标改正量相近的情况下,测站PCO影响如图 5所示。
|
| 图 5 测站PCO影响示意图 |
由图 5可得
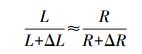 (6)
(6) 式中,L+ΔL为测站的天线相位中心移动后所形成的基线长度;L为原来的基线长度;R+ΔR为测站的天线相位中心移动后天线相位中心到地心的距离;ΔR测站的天线相位中心移动的距离。当ΔR值取40 mm、R值取6378 km、基线长度在300 km左右时,ΔL为-2 mm;当基线长度在4000 km时,ΔL为-32 mm。ΔL=-2 mm与表 1中不包含WIDC的长基线的ΔL值基本相符;ΔL=-32 mm与表 1中超长基线KOKB—THTI的ΔL值基本相符。
3.2 改正卫星天线PCO、PCV和接收机天线PCO的基线解算结果将对卫星天线PCO、PCV和接收机天线PCO、PCV进行改正的基线解算结果与对卫星天线PCO、PCV和接收机天线PCO进行改正的基线解算结果作差,结果见表 3。
| mm | |||||
| 测站1 | 测站2 | 平均 | |||
| ΔX | ΔY | ΔZ | ΔL | ||
| BLYT | SBCC | -0.000 1 | 0.001 4 | -0.000 2 | 0.000 7 |
| BLYT | WIDC | 0.012 5 | 0.025 1 | -0.016 1 | 0.000 0 |
| GOLD | SBCC | 0.000 2 | 0.000 6 | -0.001 1 | 0.000 5 |
| GOLD | WIDC | 0.012 8 | 0.024 2 | -0.017 0 | -0.001 3 |
| POTR | SBCC | 0.003 7 | 0.008 1 | -0.004 7 | 0.001 0 |
| POTR | WIDC | 0.016 3 | 0.031 7 | -0.020 6 | 0.002 4 |
| SBCC | WIDC | 0.012 6 | 0.023 6 | -0.015 9 | 0.000 9 |
| ALIC | COCO | 0.005 4 | 0.009 6 | 0.003 2 | 0.010 0 |
| ALIC | MAC1 | -0.002 7 | -0.002 9 | -0.012 5 | 0.010 0 |
| COCO | LHAZ | 0.000 4 | -0.011 2 | 0.008 9 | 0.010 3 |
| KOKB | THTI | -0.008 0 | -0.009 0 | -0.019 2 | 0.020 1 |
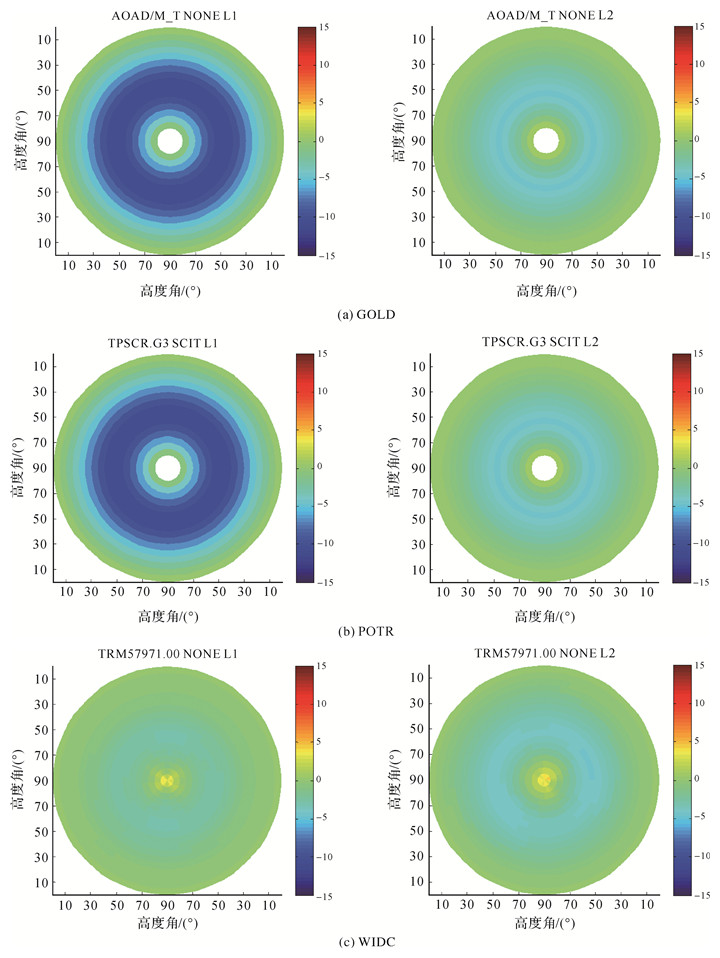
由表 3可知,对于长基线ΔL最大不超过2.5 mm,但是包含测站WIDC的基线,基线分量偏差ΔX、ΔY、ΔZ能达到厘米级,最大可达到3.2 cm,其他长基线的基线分量偏差ΔX、ΔY、ΔZ均在毫米级。这是因为BLYT、GOLD、IID2、JPLM、POTR、SBCC测站天线PCV参数相近,而WIDC测站天线PCV参数与其他测站天线PCV参数差异较大。图 6展示了GOLD、POTR和WIDC 3个测站天线PCV,可明显看出WIDC测站天线PCV在L1上与GOLD和POTR天线的差异。
|
| 图 6 GOLD、POTR、WIDC测站PCV |
由表 3可知,对于超长基线的影响不管是基线分量偏差ΔX、ΔY、ΔZ还是基线长度偏差ΔL,均能达到厘米级,最大可达到1.9 cm。虽然ALIC和LHAZ两测站天线PCV参数相近,COCO、KOKB、MAC1、THTI 4测站天线PCV参数相近,但是基线KOKB-MAC1在ΔZ和ΔL上均存在2 cm左右的偏差。这是因为基线长度在300 km左右时,基线两端测站观测到的同一个卫星的高度角和方位角大小相近;在测站天线PCV又相近的情况下,在组成差分观测值时能正好将测站天线PCV改正项抵消掉,而测站天线PCV差异较大时则不能抵消掉;然而在基线长度大于2000 km左右时,基线两端测站观测到的同一个卫星的高度角和方位角大小差异已经很大,不管基线两端点测站天线PCV相同与否,在组成差分观测值时测站天线PCV改正项都无法抵消掉。
3.3 改正卫星天线PCV和接收机天线PCO、PCV的基线解算结果将对卫星天线PCO、PCV和接收机天线PCO、PCV进行改正的基线解算结果与对卫星天线PCV和接收机天线PCO、PCV进行改正的基线解算结果作差,结果见表 4。
| m | |||||
| 测站1 | 测站2 | 平均 | |||
| ΔX | ΔY | ΔZ | ΔL | ||
| BLYT | GOLD | 0.001 5 | -0.002 9 | -0.000 4 | -0.002 9 |
| BLYT | POTR | 0.001 5 | -0.000 6 | 0.001 4 | -0.002 1 |
| BLYT | SBCC | 0.002 2 | -0.002 1 | 0.001 3 | -0.002 9 |
| BLYT | WIDC | 0.001 2 | -0.001 4 | 0.000 4 | -0.001 7 |
| ALIC | COCO | -0.040 0 | -0.004 1 | -0.014 8 | -0.039 1 |
| ALIC | MAC1 | -0.006 5 | 0.029 9 | 0.016 8 | -0.034 0 |
| COCO | LHAZ | 0.013 2 | -0.034 1 | -0.021 4 | -0.014 3 |
| KOKB | THTI | -0.025 6 | -0.008 4 | 0.035 6 | -0.034 3 |
由表 4可知,卫星天线PCV对长基线的影响不管是基线分量偏差ΔX、ΔY、ΔZ还是基线长度偏差ΔL均在毫米级,最大不超过4 mm;对超长基线的影响不管是基线分量偏差ΔX、ΔY、ΔZ还是基线长度偏差ΔL均在厘米,最大能达到4 cm。造成这种差异的原因是基线长度在300 km左右时,由同一个卫星观察基线两端测站的低点角和方位角大小相近,在组成差分观测值时能正好将卫星天线PCO改正项抵消掉;然而在基线长度大于2000 km左右时,由同一个卫星观察基线两端测站的低点角和方位角相差较大,在组成差分观测值时卫星天线PCO改正项无法抵消掉。
3.4 改正卫星天线PCO和接收机天线PCO、PCV的基线解算结果将对卫星天线PCO、PCV和接收机天线PCO、PCV进行改正的基线解算结果与对卫星天线PCO和接收机天线PCO、PCV进行改正的基线解算结果作差,结果见表 5。
| m | |||||
| 测站1 | 测站2 | 平均 | |||
| ΔX | ΔY | ΔZ | ΔL | ||
| BLYT | GOLD | 0.000 2 | 0.000 5 | 0.000 0 | 0.000 2 |
| BLYT | POTR | 0.000 0 | 0.000 4 | -0.000 3 | 0.000 2 |
| BLYT | SBCC | 0.000 2 | 0.000 7 | -0.000 4 | 0.000 2 |
| BLYT | WIDC | 0.000 1 | 0.000 4 | -0.000 2 | 0.000 1 |
| ALIC | COCO | -0.004 7 | -0.000 6 | -0.001 4 | 0.007 4 |
| ALIC | MAC1 | -0.001 4 | 0.000 6 | -0.002 7 | 0.007 0 |
| COCO | LHAZ | 0.002 4 | -0.001 1 | 0.005 8 | 0.007 9 |
| KOKB | THTI | -0.019 1 | -0.008 1 | 0.001 4 | 0.009 3 |
由表 5可知,卫星天线PCV对长基线的影响不管是基线分量偏差ΔX、ΔY、ΔZ还是基线长度偏差ΔL基本在毫米以下,最大值为1 mm;对超长基线的影响不管是基线分量偏差ΔX、ΔY、ΔZ还是基线长度偏差ΔL大部分在毫米级,仅基线KOKB—THTI在X方向达到2 cm。这是因为基线长度在300 km左右时,由同一个卫星观察基线两端测站的低点角和方位角大小相近,在组成差分观测值时能正好将卫星天线PCV改正项抵消掉;然而在基线长度大于2000 km左右时,由同一个卫星观察基线两端测站的低点角和方位角相差较大,在组成差分观测值时卫星天线PCV改正项无法抵消掉。
综上分析,卫星天线PCO、PCV和接收机天线PCO、PCV对高精度基线解算的影响见表 6。
| 改正项 | 长基线 | 超长基线 | |||
| |ΔXYZ| | |ΔL| | |ΔXYZ| | |ΔL| | ||
| 接收机天线PCO | 0~58 mm | <4 mm | 3~101 mm | 34~73 mm | |
| 接收机天线PCV | 0~32 mm | <3 mm | 0~20 mm | 10~21 mm | |
| 卫星天线CO | <4 mm | <4 mm | 4~36 mm | 14~40 mm | |
| 卫星天线CV | <1 mm | <1 mm | 0~20 mm | 7~10 mm | |
综上可知,接收机天线PCO、PCV对长基线解算,在基线各分量上的影响可达到厘米,对基线长度的影响小于4 mm,对超长基线解算,在基线各分量上的影响在厘米水平,最大可达到10 cm,对基线长度的影响在厘米水平;卫星天线PCO、PCV对于长基线解算,在各分量和长度上的影响均在毫米水平,其中卫星天线PCV的影响基本可以忽略不计,但是对于超长基线解算,在各分量和长度上的影响均可达到厘米。此外,对于长基线,当基线两端测站接收机天线PCO对测站坐标U方向的改正量相近时,测站天线PCO的影响不会很好地反映出来,当基线两端测站接收机天线PCV相近时,测站天线PCV的影响也不会很好地反映出来,此时可以通过仅改正基线两端测站中的一个测站将该影响体现出来。
| [1] | 朱智勤, 李征航, 刘万科. 相位中心改正模式的转变对GPS数据处理的影响[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1301–1304. |
| [2] | BILICH A L, MADER G L. GNSS Absolute Antenna Calibration at the National Geodetic Survey[J]. American Geophysical Union, 2009(3): 308–312. |
| [3] | SCHMID R, ROTHACHER M. Estimation of Elevation-dependent Satellite Antenna Phase Center Variations of GPS Satellites[J]. Journal of Geodesy, 2003, 77(7): 440–446. |
| [4] | WVBBENA G, SCHMITZ M, BOETTCHER G, et al. Absolute GNSS Antenna Calibration with a Robot:Repeatability of Phase Variations, Calibration of GLONASS and Determination of Carrier-to-Noise Pattern[C]//Processing of the IGS Workshop.Darmstod:ESOC, 2006. |
| [5] | SCHMID R, ROTHACHER M, THALLER D, et al. Absolute Phase Center Corrections of Satellite and Receiver Antennas[J]. GPS Solutions, 2005, 9(4): 283–293. DOI:10.1007/s10291-005-0134-x |
| [6] | ZHU S Y, MASSMANN F H, YU Y, et al. Satellite Antenna Phase Center Offsets and Scale Errors in GPS Solutions[J]. Journal of Geodesy, 2003, 76(11): 668–672. |
| [7] | SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a Consistent Absolute Phase-center Correction Model for GPS Receiver and Satellite Antennas[J]. Journal of Geodesy, 2007, 81(12): 781–798. DOI:10.1007/s00190-007-0148-y |
| [8] | GE M R, GERD G. Estimation and Validation of the IGS Absolute Antenna Phase Center Variations[R].[S.l.]:IGS, 1999. |
| [9] | HERRING T A, KING R W, MCCLUSKY S C. GAMIT Reference Manual:release 10.4[M].[S.l.]:MIT. 2010. |
| [10] | 王坚, 高井祥, 王金岭. 基于经验模态分解的GPS基线解算模型[J]. 测绘学报, 2008, 37(1): 10–14. |
| [11] | 郑作亚, 韩晓冬, 黄珹, 等. GPS基线向量的非线性解算及精度分析[J]. 测绘学报, 2004, 33(1): 27–32. |
| [12] | 姚宜斌. GPS精密定位定轨后处理算法与实现[D]. 武汉: 武汉大学, 2004. |
| [13] | HU C W, CHEN W, GAO S H, et al. Data Processing for GPS Precise Point Positioning[J]. 南京航空航天大学学报(英文版), 2005, 22(2): 124–131. |
| [14] | 张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250–256. DOI:10.11947/j.AGCS.2015.20130771 |
| [15] | 叶世榕. GPS非差相位精密单点定位理论与实现[D]. 武汉: 武汉大学, 2002. |
| [16] | 许长辉, 高井祥, 周锋, 等. 精密单点定位的可靠性研究[J]. 武汉大学学报(信息科学版), 2012, 37(6): 709–713. |


