2. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
由于卫星导航系统具有重大的国家战略意义,同时蕴藏着巨大的国内国际经济利益,因此世界各大工业国无一不在实施或计划自己的卫星导航系统。我国作为目前世界上举足轻重的政治、军事和经济大国当然也不例外,北斗卫星导航系统就是我国目前正在实施、自主研发、独立运行的全球卫星导航定位系统,在国际上被称为BeiDou,目前与美国的GPS、俄罗斯的GLONASS和欧盟的Galileo并列为全球四大GNSS系统。随着这四大系统的逐步完善,未来的导航星座卫星将包含120多颗卫星,并且提供多个无线电频率的信号。多频多模组合定位大大增加了可用卫星的数量,优化了卫星的空间结构,从而进一步提高了定位的精度,因此正在逐步成为研究的热点。
国内外许多专家学者都曾对北斗和GPS组合单点定位作了分析与试验[1-4]。但是有些研究成果均是利用仿真的星座与数据,有些虽然利用实测数据,但是均是分析组合定位在单个测站的性能。很少有文章站在全球的角度,全面地评价与分析北斗与GPS组合定位相对于单一系统的优势。另外,目前北斗卫星导航系统的建设已经完成了第二步,正处于第三步——全球组网的实施阶段[5]。最近几年正是北斗卫星密集发射的阶段,因此有必要经常监测、评价与分析北斗卫星的性能。鉴于此,本文开展北斗与GPS的组合单点定位的研究,以期能够为北斗的应用推广提供参考。
1 北斗+GPS组合单点定位解算模型 1.1 时间基准的统一GPS时间是GPS系统运作的时间基准,简称为GPST。GPST从本质来说是一种原子时。第一个GPS时开始于1980年1月5日午夜和1月6日凌晨交接的时刻,即UTC时间1980年1月6日的0:00:00。此后,GPST和UTC时的偏差就越来越大,2012年7月1日以后,GPST与UTC之间的差异已经达到16 s,即
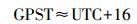 (1)
(1) 式(1) 中的近似号是因为GPST和UTC除了由于跳秒累积产生的整秒差异之外,还存在着小于1 μs的秒内偏差,而该偏差可以通过GPS卫星广播星历的UTC时间参数计算得到。
根据2012年12月27日公开的北斗接口控制文档1.0版,BDT以国际单位制秒为基本单位进行时间累积,没有跳秒,因此与GPST一样,BDT是连续时间。BDT的起始历元是UTC时间2006年1月1日00:00:00,对应的儒略日为2 453 736。考虑到BDT起始历元的时刻,GPST的星期数和周内秒计数为:GPST=[1356周,14.000 s]。因此,可以推断出BDT和GPST有如下关系
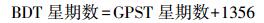 (2)
(2) 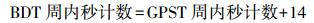 (3)
(3) 式(3) 在计算时需要考虑溢出的问题,即当GPST周内秒数计数+14超过604 800时需要将BDT星期数加1[6]。
1.2 空间基准的统一由于各个国家在建立各自卫星导航系统的同时,也建立了自己独立的空间基准,因此在进行组合导航定位时一定要统一空间基准。GPS采用的是WGS-84[7],北斗系统采用的是2000国家大地坐标系(CGCS2000)。这两个坐标系统所定义的原点、尺度、定向及定向演变的尺度都是相同的,它们与IRTF紧密相关。WGS-84最初实现时,精度约为1 m,经过两次优化之后精度已达2 cm,与ITRF精度基本一致,甚至小于WGS-84本身的系统误差。CGCS2000与ITRF的一致性约为5 cm,因此WGS-84与CGCS2000的差异在厘米级[8]。对导航等绝大多数非精密定位应用来讲,WGS-84和CGCS2000这两个空间坐标系通常被认为是相互一致的,它们之间无需任何坐标转换。本文单点定位的精度在米级,因此无需进行两个坐标系统的转换,直接把它们视为同一坐标系即可[9]。
1.3 组合单点定位模型GNSS伪距定位的方程式如下
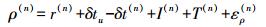 (4)
(4) 式中,ρ(n)为卫星n至接收机u之间的伪距测量值;r(n)为卫星天线相位中心至接收机天线相位中心的几何距离;δtu为接收机的钟差;δt(n)为卫星钟差;I(n)为电离层延迟;T(n)为对流层延迟;ερ(n)为伪距测量的噪声。
可将式(4) 改写成如下的误差校正后的GNSS伪距观测方程式
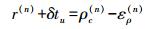 (5)
(5) 式中,误差校正后的伪距测量值ρc(n)为
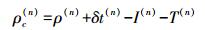 (6)
(6) 式(5) 中,所有未知量(不计测量噪声参量ερ(n))和已知量被分别转移到了等号的左右两边,这为GNSS伪距定位解算厘清了思路[10]。
将GPS时间tGPS与BD系统时间tBD之间的差异记为δtGPS-BD,其定义为
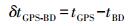 (7)
(7) 校正后的GPS和BD伪距观测方程式分别为
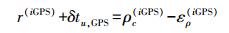 (8)
(8)  (9)
(9) 误差校正后的GPS和BD伪距观测值分别为
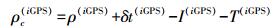 (10)
(10) 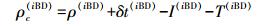 (11)
(11) 将以上两式线性化后可以建立一个如下的BD/GPS联合定位矩阵方程式
 (12)
(12) 式(12) 中
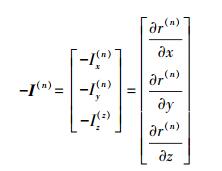 (13)
(13) 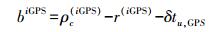 (14)
(14) 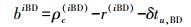 (15)
(15) 式(13) 中, (x, y, z)为接收机的坐标。利用以上方法即可求出接收机的坐标[11-13]。
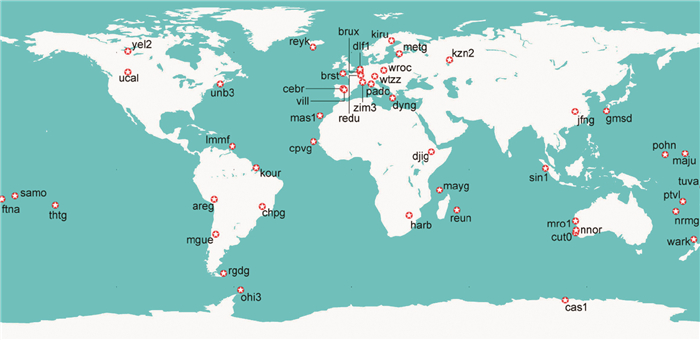
2 实测数据处理与分析由于北斗卫星正在持续建设之中,为了验证近期北斗系统整体定位的效果,本次试验数据采用的是2016年1月8日全球的MGEX网所采集到的北斗和GPS数据。MGEX网测站全球分布如图 1所示[14]。由于MGEX网中测站的精确坐标没有发布,因此本文利用Bernese软件中精密单点定位的功能解算出所需测站的ITRF坐标。由于Bernese软件解算出的坐标精度可以达到厘米级至毫米级,而伪距单点定位的精度一般在米级左右,因此解算出的坐标可以作为真值,与利用北斗和GPS组合单点定位算法解算的结果作比较。
|
| 图 1 MGEX跟踪网全球分布 |
本文采用两种方案来验证北斗+GPS组合单点定位的性能。
(1) 选择单个测站,分别利用北斗、GPS、北斗+GPS 3种数据解算该测站的坐标。得到该测站全天所有历元解算的结果,精密单点定位的坐标作差,并作比较分析。
(2) 在亚太地区选择12个能同时接收到的北斗和GPS数据的测站,分别利用北斗、GPS和北斗+GPS 3类数据计算测站的坐标。得到每个测站一天的平均值,评价北斗、GPS和北斗+GPS 3种解算方法的性能。
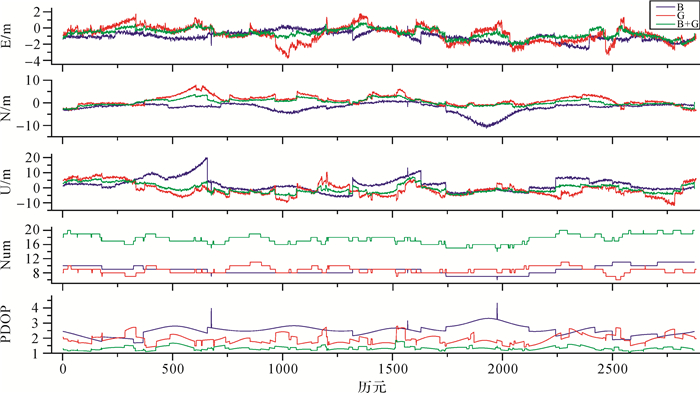
2.1 北斗+GPS在单个测站的性能分析到目前为止,北斗卫星主要覆盖在亚太地区,且已经能够在这一地区完成导航定位的功能。因此本文选择中国境内jfng测站来进行组合定位的性能分析。利用2016年1月8日jfng全天的数据,分别利用北斗、GPS和北斗+GPS来解算这个测站的坐标。数据采样间隔为30 s,卫星截止高度角为10°。所得到的测站E、N、U方向的均方根误差、卫星平均个数(Num)及PDOP的平均值如图 2所示。其中B代表单独利用北斗数据解算的结果,G代表单独利用GPS数据的解算结果,B+G代表利用北斗+GPS组合定位解算的结果(下同)。
|
| 图 2 测站jfng E、N、U方向的均方根误差、卫星个数及PDOP值随历元变化 |
表 1给出了利用这3种方法解算所得到的jfng测站东北天3个方向的均方根误差的数值,以及3种方法中全天平均卫星的个数、PDOP的平均值。其中最后一列代表的是北斗+GPS组合定位分别相对于北斗单系统、GPS单系统的提高率。
| 参数 | BDS | GPS | BDS+GPS | 提高率/(%) |
| E/m | 1.201 0 | 1.217 1 | 0.868 5 | 27.7/28.6 |
| N/m | 2.969 5 | 2.327 0 | 1.447 5 | 51.3/37.8 |
| U/m | 4.717 0 | 4.369 4 | 2.996 1 | 36.5/31.4 |
| 平均卫星数 | 8.746 4 | 8.788 2 | 17.534 3 | 100.5/99.5 |
| PDOP | 2.498 1 | 1.936 5 | 1.334 2 | 46.6/31.1 |
从图 2和表 1中可以看出,在E方向上,北斗+GPS组合定位精度最高,与北斗解算相比提高了27.7%,与GPS相比提高了28.6%,北斗解算的精度要高于GPS解算的精度,这与北斗在东西方向上分布5颗GEO卫星有关,大大增强了北斗东西方向的结构强度;在N方向上,北斗+GPS组合定位精度最高,与北斗解算相比提高了51.3%,比GPS提高了37.8%,GPS解算精度要高于北斗解算的精度;在U方向上,北斗+GPS组合定位精度最高,比北斗解算提高了36.5%,比GPS解算提高了31.4%,北斗解算精度要低于GPS解算的精度。利用这3种方法解算,E方向的精度均高于N方向的精度和U方向上的精度。
从图 2中也可以看出,北斗卫星的稳定性不如GPS,北斗+GPS组合系统的稳定性最高。表 1中显示,北斗系统的PDOP值高于GPS,GPS的PDOP值高于组合系统,这是因为虽然北斗系统能够在亚太地区提供定位服务,但是并没有完成全球的组网,卫星分布不如GPS均匀,而组合定位中卫星的个数是比单系统增加了一倍,大大增加了导航卫星的个数,增强了卫星几何图形的空间强度,从而降低了PDOP值。
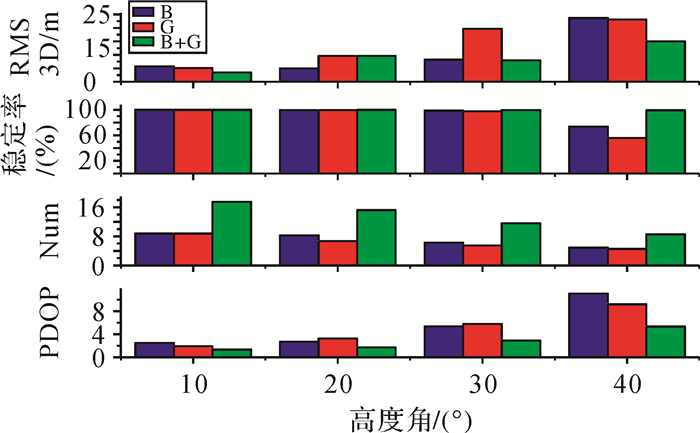
另外,多系统组合的另一个比较大的优势就是在有遮挡物的情况下,比如在城市峡谷中,低高度角度的卫星被遮挡情况下仍然能够正常运行。因此本文作了如下的试验,计算卫星截止高度角分别为10°、20°、30°、40°的情况下,测站的三维位置均方根误差,定位的稳定率,卫星的平均个数,平均PDOP值。其中,稳定率=成功解算的历元个数/总历元的个数。其结果如图 3所示。
|
| 图 3 测站jfng三维位置均方根误差、稳定率以及平均卫星个数和PDOP值随高度角变化 |
从图 3中可以看出,随着截止卫星高度角的增加,定位的三维位置误差在不断增大,但是组合定位的精度总是高于单系统定位的精度。当截止高度角达到40°以后,单系统三维位置误差会达到25 m左右,而北斗+GPS组合定位的位置误差虽然也在增加,但是在15 m左右,远小于单系统的定位误差。卫星截止高度角在30°以下时,对解算的稳定率影响不大,继续增加卫星截止高度角,单系统稳定性急剧下降,而北斗+GPS定位的稳定性依然很高。这是因为虽然卫星截止高度角增加,但是组合系统卫星的数量依然是单系统的两倍,因此仍然能够成功地解算出测站坐标。另外,卫星截止高度角的增加,会使得PDOP值急剧上升,但是组合系统的PDOP值仍然小于单系统的值。从图 3中可以看出,即使高度角增大组合系统的定位精度和稳定率都要高于单系统。
2.2 北斗+GPS在亚太地区的性能分析由于北斗卫星导航系统正在建设当中,全球组网刚刚开始,为了全面评价北斗及北斗+GPS组合定位的性能,选用亚太地区及其周边的一些能够同时接收北斗与GPS信号的MGEX网中的测站来全面地评价其性能。
表 2是12个测站3种计算方法在E、N、U方向的平均误差、卫星的平均个数及PDOP的平均值。
| 参数 | BDS | GPS | BDS/GPS | 提高率(%) |
| E/m | 6.183 2 | 1.332 6 | 1.093 9 | 82.3/17.9 |
| N/m | 4.168 7 | 1.998 5 | 1.343 3 | 67.8/32.8 |
| U/m | 13.091 5 | 4.281 0 | 3.922 5 | 69.5/6.7 |
| 平均卫星数 | 6.111 6 | 8.845 2 | 14.527 6 | 137.7/64.24 |
| PDOP | 6.090 7 | 1.956 5 | 1.458 7 | 76.1/25.4 |
由图 4可以看出,所选的12个测站北斗导航系统的定位精度很不稳定,有几个测站(如cas1、kzn2、samo、zim3) 精度较差,这与测站所处的地理位置有关。这几个测站都处在欧洲地区或亚太地区附近,导致所接收到的北斗卫星的个数较少,观测值较少,从而精度降低。从这12个测站的定位情况中可以看出,GPS的位置精度和稳定性都要高于北斗,组合单点定位的精度最高。北斗+GPS组合定位精度相对于北斗的提高幅度要远大于相对于GPS的提高幅度。说明我国北斗系统之中仍然存在许多误差项需要不断的优化[17]。
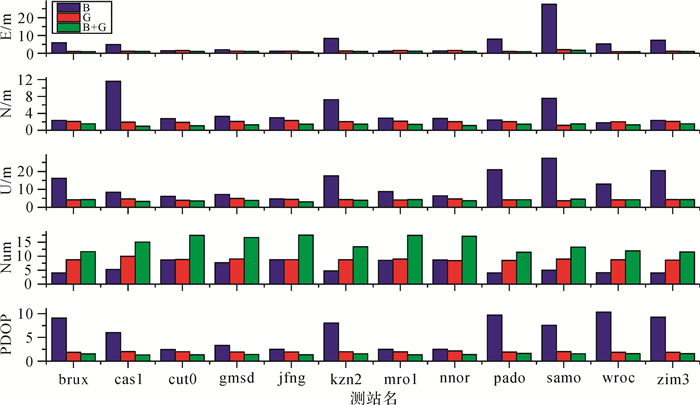
|
| 图 4 12个测站的东北天(ENU)方向均方根误差、平均卫星个数及POP值 |
我国北斗卫星导航系统已经进入了全球组网的阶段,正在如火如荼的建设当中,本文利用实测数据,通过方案设计可以得到如下结论:
(1) 北斗+GPS组合单点定位在E、N、U 3个方向的精度和稳定性均优于北斗和GPS单系统。
(2) 北斗+GPS组合系统的卫星个数是单系统卫星个数的两倍,组合系统的PDOP值远小于单系统的PODP值。组合系统在卫星截止高度角增加的情况下,优势明显,定位精度和稳定性优于单系统。尤其是在卫星截止高度角较高的情况下,远优于单系统的定位精度和稳定性。
(3) 虽然北斗在亚太地区已经能够提供定位服务,但是北斗单系统定位的精度和稳定性均低于GPS单系统定位的精度。说明北斗系统中还有很多地方需要完善。
随着北斗卫星星座的逐步完善,相信北斗单系统和北斗+GPS组合单点定位的精度都会有所提高。如何利用全球多个系统进行组合单点定位,以及利用多个系统进行精密单点定位将成为下一步研究的重点。
| [1] | 黄丽霞. GPS、北斗卫星导航系统组合单点定位模型及算法[J]. 电子科技, 2014, 27(7): 23–25. |
| [2] | 安向东. GPS与北斗伪距单点定位性能对比分析[J]. 全球定位系统, 2014(3): 8–14. |
| [3] | 陆亚峰, 楼立志, 马绪瀛, 等. 北斗与GPS组合伪距单点定位精度分析[J]. 全球定位系统, 2013(6): 1–6. |
| [4] | 李彬, 李征航, 刘万科. COMPASS/GPS/GLONASS系统组合在中国区域的仿真分析[J]. 大地测量与地球动力学, 2013, 33(6): 94–97. |
| [5] | 龙昌生. 北斗/GPS双模导航终端关键模块的设计与实现[D]. 重庆: 重庆大学, 2011. |
| [6] | 陈杨毅. GPS与BD双模GNSS接收机定位解算技术研究[D]. 厦门: 厦门大学, 2014. |
| [7] | AGENCY M. United States Department of Defense, World Geodetic System 1984:Its Definition and Relationships with Local Geodetic Systems[R].[S.l.]:NIMA, 2000. |
| [8] | SEGUY J. Maintenance and Enhancement of the World Geodetic System 1984[J]. Proceedings of ION GPS-94, 1994(37): 244–245. |
| [9] | ABUSALI P A M, SCHUTZ B E, TAPLEY B D, et al. Transformation between SLR/VLBI and WGS-84 Reference Frames[J]. Journal of Geodesy, 1995, 69(2): 61–72. |
| [10] | BURWELL R M. Magellan Announces the GPS Companion for the Handspring Visor[J]. Critique Studies in Contemporary Fiction, 2013, 15(1): 48–58. |
| [11] | KAI B, DENNIS A A. A Software Defined GPS and Galileo Receiver[M]. Boston: Birkhäuser, 2007. |
| [12] | CHANGSHENG C. A Combined GPS/GLONASS Navigation Algorithm for Use with Limited Satellite Visibility[J]. Journal of Navigation, 2009, 62(4): 671–685. DOI:10.1017/S0373463309990154 |
| [13] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines Up to 2000 km[J]. Journal of Geophysical Research (Solid Earth), 1989, 94(B8): 10187–10203. DOI:10.1029/JB094iB08p10187 |
| [14] | PAN L, CAI C, SANTERRE R, et al. Performance Evaluation of Single-frequency Point Positioning with GPS, GLONASS, BeiDou and Galileo[J]. Survey Review, 2016: 1–9. |
| [15] | 高星伟, 过静珺, 程鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J]. 测绘学报, 2012, 41(5): 743–748. |


