精确的轨道位置可以提高导航系统的各项服务和用户的定位精度,除了动力学模型、定轨方法等对导航卫星的轨道和钟差有影响之外,地面跟踪站的数量和分步也对定轨精度产生了一定的影响。如今随着GNSS的融合与卫星精密定轨技术的逐步发展,越来越多的观测站点被建立,其中IGS和iGMAS全球观测站点的数量已超过500个。因此如何在保障定轨精度的情况下,有效剔除冗余的测站,提高计算效率显得尤为重要。本文首先介绍了测站选取的方法,然后利用编制的选站软件结合GPS实测数据,开展了定轨试验,并进一步分析了定轨精度[1-5]。
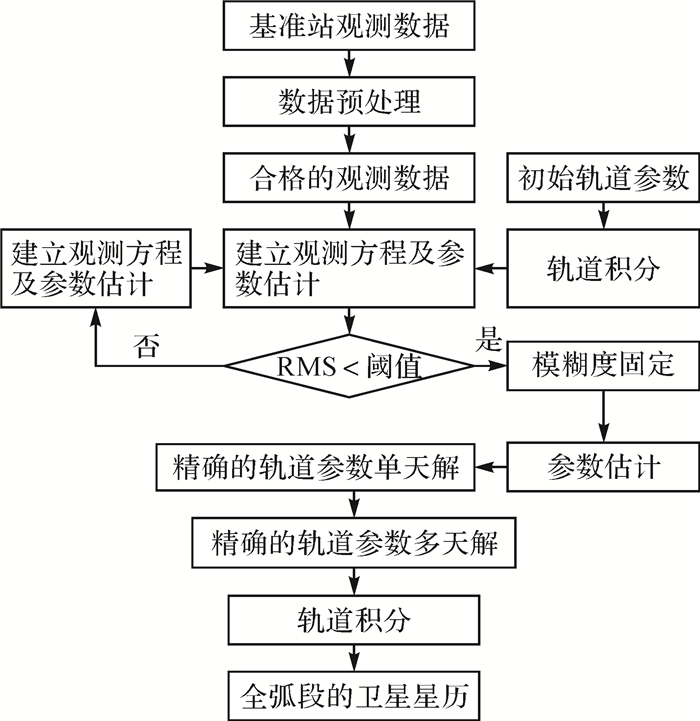
1 数据处理 1.1 卫星轨道解算方法卫星轨道位置的确定可以分为三步:①对观测数据进行预处理;②建立观测方程,进行参数的估计,得到某个时刻卫星的精确状态参数;③对这个时刻卫星的轨道参数进行积分,得到其他时刻的卫星位置[6-9]。卫星定轨的基本流程如图 1所示。
|
| 图 1 卫星位置计算流程 |
为了得到高精度的定轨结果,必须对测站的选取方法进行合理、严密的分析。综合国内外的研究选点基本标准,首先应进行测站的初选,测站在近几年必须是连续观测,将处理过程中不连续和观测质量较差的点删除;对基准站的观测数据进行处理之后,得到站点坐标时序稳定性好,并具有稳定的点位变化速度,速度场精度优于3 mm/a。然后进行站点的进一步精选,采用七参数法精选站点,以板块运动模型划分的合理板块地界作为地学资料,基准站的速度可以表示为[10]
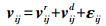 (1)
(1) 式中,vij表示第j板块上第i测站的观测速度;vijr表示刚性板块的运动速度;vijd表示区域地壳刚性板块运动速度;εij表示观测噪声引起的速度。
其中
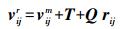 (2)
(2) 式中,vijm是由板块运动模型得到的;T=[Tx Ty Tz];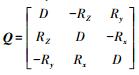
这样则有
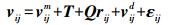 (3)
(3) 忽略区域性地壳形变与观测噪声的影响,写成误差方程形式得
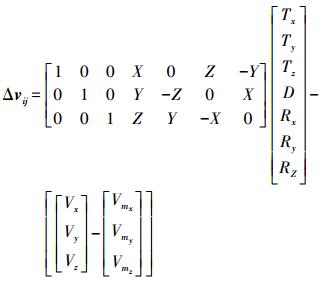 (4)
(4) 平差模型为间接平差:V=BX-L,因此可以得到X=(BTB)-1BTL,将X代入式中求得站点残差项Δvij,剔除站点残差Δvij大于σ的站点。
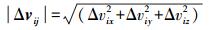 (5)
(5) 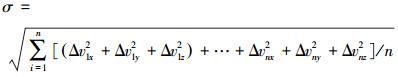 (6)
(6) 在同一个板块上,基准站在空间上的变化是逐渐的,因此各站的速度大小和方向应当一致。据此对测站进行剔除,同样以合理的板块划分边界作为地学资料约束。
首先将地心参考坐标转化为站心坐标下的水平站速度 (Ve,Vn), 利用最小二乘原理重新计算板块内的欧拉参数。然后利用求出的欧拉参数求得测站的模型速度,并计算它的方位角,再分别与实际的速度和方位角相比较,剔除残差项大于σ′和σ″的测站,直至满足条件的测站都被剔除[11]。
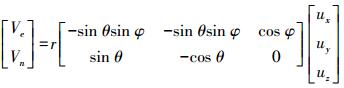 (7)
(7) 式中,r为测站到地心的距离;θ为站点的纬度;φ为站点的经度。
即为
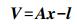 (8)
(8) 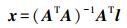 (9)
(9) 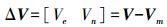 (10)
(10) 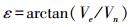 (11)
(11) 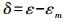 (12)
(12) 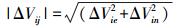 (13)
(13) 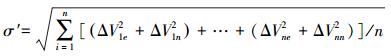 (14)
(14) 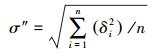 (15)
(15) 式中, σ′为板块内测站模型速度残差的中误差; σ″为方位角残差中误差; ε为速度的方位角。
2 算例分析本文的观测数据采用的是全球的IGS观测网数据,观测时间为2015-08-02—2015-08-04(年积日186-188)。为了验证上述基准站选取方法的可靠性,顾及测站的分布及密度,进行了不同的定轨试验,并对其定轨精度进行了统计与分析。
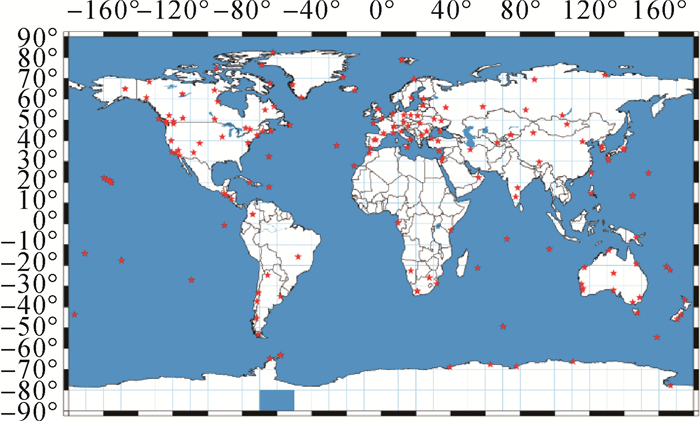
2.1 顾及测站分布经过上述方法选择之后 (如图 2所示),测站在全球的分步是不均匀的,尤其是欧洲地区。为了研究测站的分布对定轨精度的影响,设计了两种定轨方案。
|
| 图 2 基准站分布 |
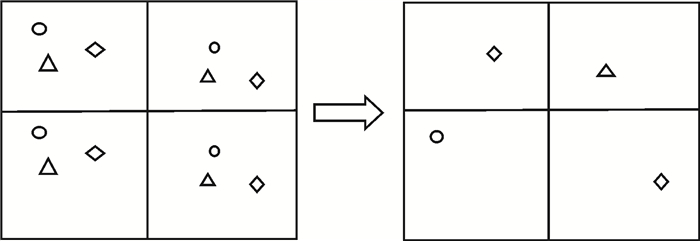
(1) 在上述选择的基准站基础上,针对测站分布较为密集的区域,根据各个测站之间的距离,将分布密集的测站抽稀以保证分区内站点的大致均匀分布。具体实现方法是采用格网分区的方法进行处理,基于要进行处理的区域范围,按照纬度和经度进行格网划分 (1°大约为111 km),将要处理的区域划分成网格区域[12-14]。然后统计每个网格内的测站数,并按照基准站观测数据质量的高低剔除多余基准站。如图 3所示。
|
| 图 3 格网选站示意 |
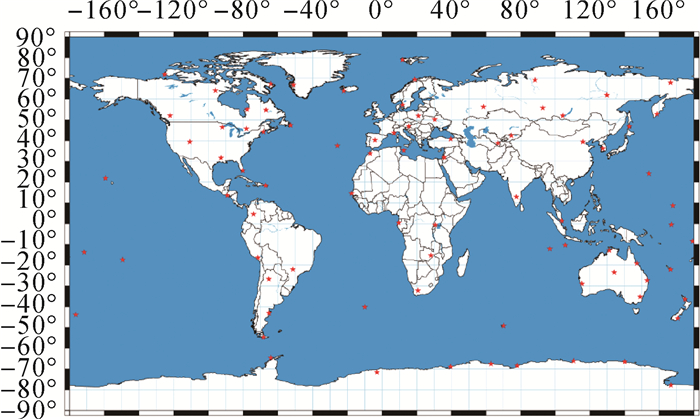
共选择了90个基准站,选择后的站点分布如图 4所示。
|
| 图 4 基准站分布 |
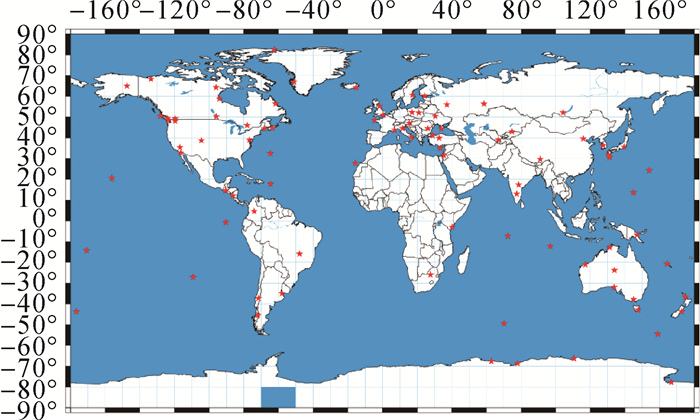
(2) 同样是在选择的测站基础上,首先使用TEQC软件对所有测站进行前期的数据预处理,然后根据TEQC处理完之后的数据质量指标,对基准站按照数据质量的高低进行选择,保证选择出与方案 (1) 同样多的站点数,90个站点。选择后的站点分布如图 5所示。
|
| 图 5 基准站分布 |
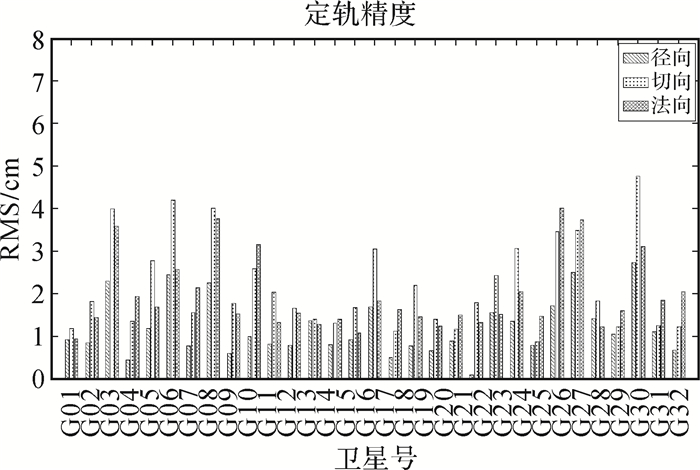
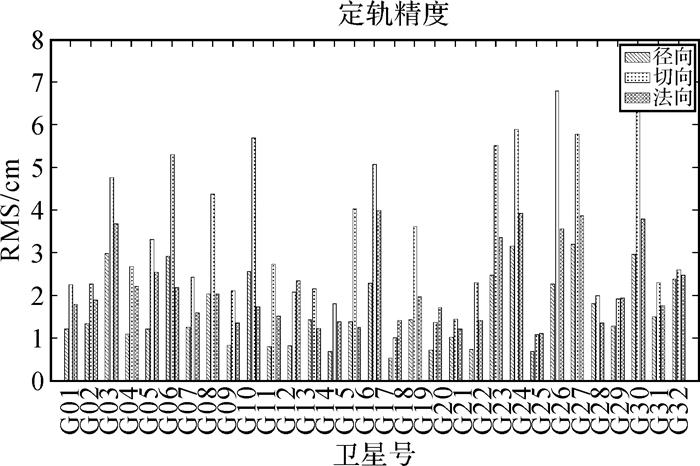
用上述两个测站分布方案进行了定轨解算,然后分别将得到的定轨结果与IGS发布的最终轨道产品进行互差,并对3个方向的均方根误差进行了统计。统计结果如图 6、图 7所示。
|
| 图 6 基准站均匀分布定轨精度 |
|
| 图 7 基准站不均匀分布定轨精度 |
统计结果表明,当采用方案 (1) 进行定轨时,计算得到的卫星位置与IGS发布的卫星精密星历在径向、切向、法向的偏差均方根分别为1.44、2.62、2.07 cm;采用方案 (2) 进行定轨时,3个方向上的偏差均方根分别为1.85、3.57、2.38 cm。可以看出,在基准站站点数量一定时,站点地理分布对于定轨结果有影响,站点地理分布越均匀,定轨精度越高。
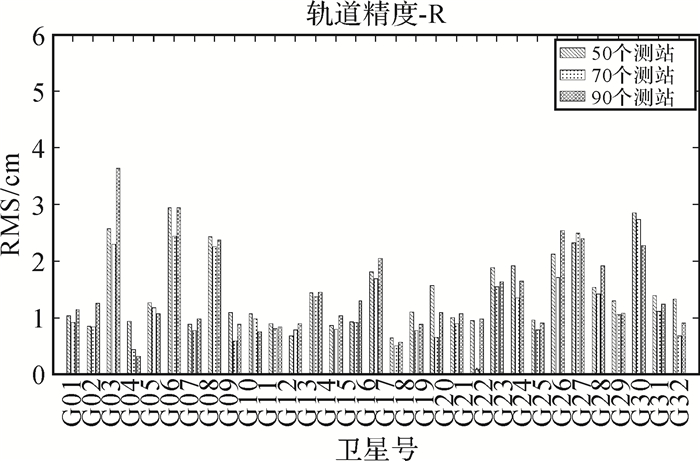
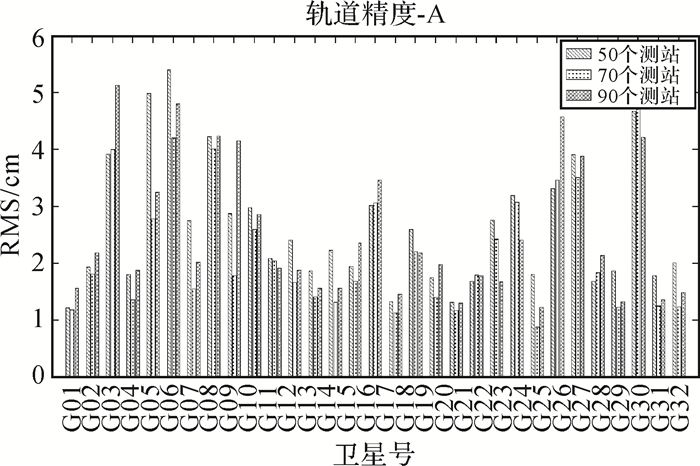
2.2 顾及测站密度为了研究测站数量对于定轨精度的影响,在上述定轨方案 (1) 均匀选择的90个测站基础上,利用格网法对基准站又进行了进一步的抽稀处理[15],多余基准站的剔除按照基准站观测数据质量的高低进行,分别得到站点个数为70与50的两种选取方案。然后将通过两种站点选取方案计算得到的定轨结果与IGS发布的最终轨道产品进行互差,并对3个方向的均方根误差进行了统计。统计结果如图 8—图 10所示。
|
| 图 8 径向方向精度 |
|
| 图 9 切向方向精度 |
|
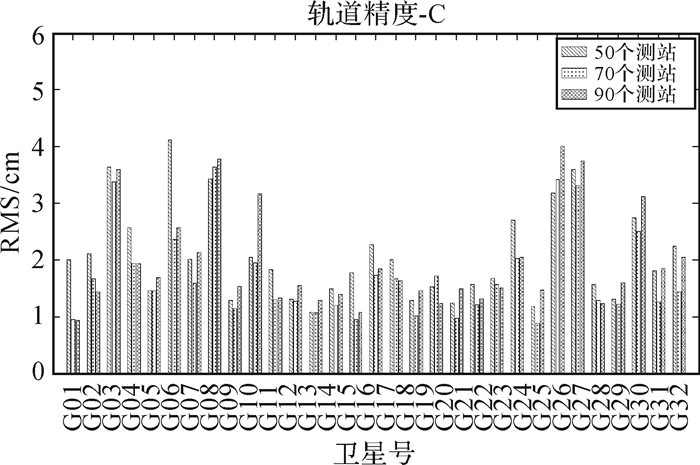
| 图 10 法向方向精度 |
统计结果表明,3种方案在径向方向上的偏差均方根分别为1.44、1.11、1.42 cm, 在切向方向上的偏差均方根分别为2.62、2.19、2.51 cm, 在法向方向上的偏差均方根分别为2.07、1.72、1.97 cm。可以看出在70个基准站时,卫星定轨精度最高,在测站分布均匀的前提下,增加基准站数量会对定轨结果产生影响,基于本文的站点选取方案,在70个站点时定轨精度最高。要综合考虑站点密度与站点的地理分布。
3 结论通过对文中几种定轨方案得到的定轨结果分析,可以得到以下几点结论:①在保证卫星和基准站观测数据良好的前提下,基准站的分布越均匀,定轨精度越高;②在保证基准站分布均匀的前提下,增加基准站数量对提高定轨精度有一定帮助,但并不是越多越好,基于文中的测站选取方法,70个站点即可得到较好的定轨精度结果;③验证了文中基准站选取方法的可靠性与有效性。该方法可以避免冗余的基准站参与定轨计算,尽量减少选站过程中的人为因素,能够在确保定轨精度的情况下,大大提高定轨的解算效率。
| [1] | 党亚民, 秘金钟, 成英燕. 全球导航卫星系统原理与应用[M]. 北京: 测绘出版社, 2007. |
| [2] | 张勤, 李加权. GPS测量原理及应用[M]. 北京: 科学出版社, 2005. |
| [3] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005. |
| [4] | 刘大杰, 施一民, 过静珺. 全球定位系统 (GPS) 的原理与数据处理[M]. 上海: 同济大学出版社, 2005. |
| [5] | 姚宜斌. GPS精密定位定轨后处理[M]. 北京: 测绘出版社, 2008: 72-75. |
| [6] | 张睿.基于地面跟踪站观测技术的GPS卫星定轨研究及程序设计[D].西安:长安大学, 2013:25-28. |
| [7] | 王武星, 顾国华. 利用基准观测资料确定GPS卫星轨道[J]. 大地测量与地球动力学, 2003, 23 (3) : 112–115. |
| [8] | 秘金钟, 党亚民, 蒋志浩, 等. 基于国家测绘局GPS连续运行参考站的定轨[J]. 辽宁工程大学学报 (自然科学版), 2009, 28 (2) : 202–205. |
| [9] | 任锴, 贾小琳, 宋小勇. Gamit定轨软件分析[C]//第二届中国卫星导航学术年会. 上海: 中国卫星导航系统管理办公室, 2011: 1-4. |
| [10] | 金双根, 朱文耀. 确定板块运动模型的台站选取[J]. 大地测量与地球动力学, 2003, 23 (3) : 56–60. |
| [11] | 高乐, 英燕, 郑作亚, 等. GNSS数据处理框架点的选取方法研究[J]. 大地测量与地球动力学, 2011, 31 (2) : 133–136. |
| [12] | 万军, 成英燕, 党亚民, 等. 陆态网测站高精度解算分区方案[J]. 测绘科学, 2016, 41 (4) : 1–4. |
| [13] | 李兵, 成英燕, 于男, 等. 密集型CORS站的高精度基线解算方案研究[J]. 测绘通报, 2014 (10) : 50–53. |
| [14] | 赵建三, 杨创, 闻德保. 利用GAMIT高精度GPS基线解算的方法及精度分析[J]. 测绘通报, 2011 (5) : 5–9. |
| [15] | 曹炳强, 成英燕, 许长辉, 等. 间距分区法在解算卫星连续运行站数据中的应用[J]. 测绘通报, 2016 (11) : 15–17. |


