2. 中国科学院遥感与数字地球研究所,北京 100101
2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
目前,无人机已经成为测绘领域获取数据的重要手段[1-2]。然而由于载荷问题,大部分无人机只能装备普通的数码相机。由于普通数码相机不是专门为量测目的而设计,因此,其畸变性能与专业的航空摄影测量中的量测相机的畸变性能不完全相同。数码影像的畸变主要由相机光学镜头的畸变与机械误差引起,常用的畸变参数有相机的径向畸变参数、切向畸变参数、像元比例尺不一致性参数和相机像元的不正交性参数[3]。这些畸变参数可以通过相机检校方法获取。全面的、高精度的畸变参数可以保证最终的航测精度,但同时在求解这些畸变参数时也需要非常苛刻的检校环境和大量的初始条件,过程也较为复杂。当条件有限时,只能获取部分畸变参数。因此,探讨不同畸变参数组合模型对像点观测精度的影响,对于无人机航测空三成果乃至整个航测工程具有重要意义。目前业内的学者开展了多项研究。张惠均、魏方震等开展了无人机的航测应用研究[4-5]。刘力荣、唐健林等研究了POS辅助条件下的航空摄影测量精度分析[6-7]。黄健、蒋春华、陈良浩等研究了航测中控制点分布对结果的影响[8-10]。程效军、崔红霞、李海滨、崔瑞兵、张烁等研究了镜头畸变参数的测定和校正方法[11-15]。但是上述学者的研究都没有开展不同畸变参数组合对航空测图结果精度的影响研究。为了研究不同条件下,不同畸变参数对像点量测精度的影响,本文采用3种不同型号的镜头开展了多种畸变参数组合下的像点量测误差统计,并得到了具有参考意义的结果,可为其他无人机航测任务提供参考。
1 畸变纠正模型数码相机的畸变参数主要包括相机径向畸变、切向畸变和CCD或CMOS面阵内变形参数。结合一定数量的高精度控制点,建立包含相机畸变参数的共线方程,通过最小二乘方法可以求解得到待求畸变参数。获取这些畸变参数后,根据不同的畸变参数组合模型可以得到不同条件下的像点坐标偏差,从而进一步研究畸变对像点观测精度的影响。
1.1 包含畸变参数的共线方程假设影像获取时刻其外方位元素的6个参数包括位置参数 (Xs, Ys, Zs)、像片倾角 (φ)、偏角 (ω) 及像片旋转角 (k),可以通过高精度控制点和空间后方交会方法直接获取[13]。假设影像中的控制点对应像点的平面直角坐标为 (x, y),控制点的地面坐标为 (X, Y, Z),待求数码相机的焦距为f,相机畸变引起的像点误差为 (Δx, Δy),则根据上述参数可以建立以下共线方程
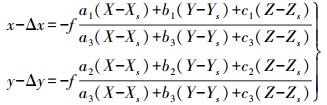 (1)
(1) 式中,ai、bi、ci(i=1, 2, 3) 为影像的3个外方位角元素φ、ω、κ组成的9个方位余弦。
像点误差采用OpenCV中的经典模型,完整的相机畸变参数与像点位移间的关系为
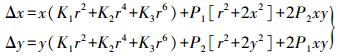 (2)
(2) 式中,K1、K2、…、Kn表示径向畸变系数;P1、P2表示切向畸变系数;r表示向径。对于普通镜头径向畸变系数一般取至K3项。
径向畸变取至3阶,将式 (1) 进行线性化,则可以得到各种畸变的误差方程为
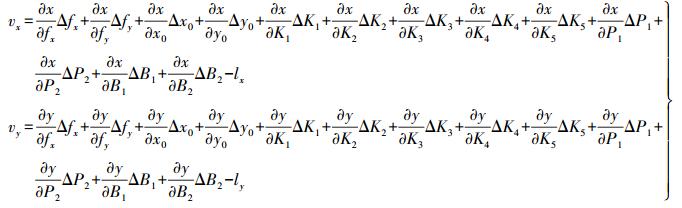 (3)
(3) 式中,(vx, vy) 为像点坐标的改正数;(Δfx, Δfy, Δx0, Δy0) 表示内方位元素的改正量;(ΔK1, ΔK2, ΔK3, ΔK4, ΔK5, ΔP1, ΔP2, ΔB1, ΔB2) 表示畸变系数的改正量;(lx, ly) 为常数项。
由式 (3) 得出的系数矩阵和常数项矩阵,结合一定数量的高精度控制点,通过最小二乘即可求解出内方位元素和各种畸变参数。
1.2 畸变参数组合模型畸变参数可以分为径向畸变、切向畸变、非方形像元改正和像素阵列的非正交改正参数。单独的径向畸变模型,取至3阶的径向畸变为 (K1, K2, K3);切向畸变差参数为 (P1, P2);非方形像元改正参数及像素阵列的非正交改正参数为 (B1, B2)。通过对不同畸变参数进行组合可以得出畸变参数对无人机航测精度的影响。
假设r为向径,(x, y) 为以像主点为原点的像点坐标。只考虑K1时的畸变改正模型为
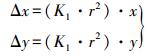 (4)
(4) 只考虑K2所在项时的畸变改正模型为
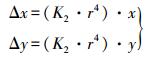 (5)
(5) 只考虑K1、K2所在项时的畸变改正模型为
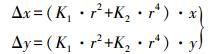 (6)
(6) 只考虑3阶的径向畸变的改正模型为
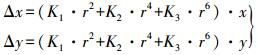 (7)
(7) 只考虑K1、K2、K3、P1、P2所在项时的畸变改正模型为
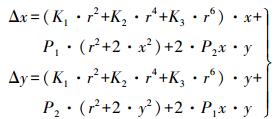 (8)
(8) 只考虑K1、K2、K3、P1、P2、B1、B2所在项时的畸变改正模型为
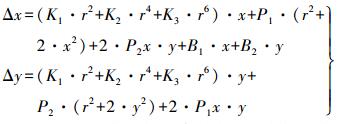 (9)
(9) 在测区四角添加平高控制点,并布设检查点进行平差,可以得到不同组合下像点的量测精度,以此来验证最优的畸变参数组合模型。
2 试验与分析为了验证上述不同组合模型的效果,采用了大疆S900旋翼无人机搭载3种不同类型的相机镜头对辽宁工程技术大学北校区进行航拍,并开展了点位精度测试。
2.1 精度测试试验首先,在实验室采用标准棋盘格标定板,通过Matlab自带标定程序,得到3种镜头的畸变参数见表 1,镜头1为佳能25 mm镜头参数值,镜头2为索尼16 mm镜头参数值,镜头3为佳能35 mm镜头参数值。
| 参数 | 镜头1 | 镜头2 | 镜头3 |
| f/mm | 24.537 9 | 16.122 5 | 35.321 8 |
| x0/mm | 0.083 7 | 0.069 5 | 0.149 7 |
| y0/mm | 0.036 5 | 0.367 5 | 0.034 3 |
| K1 | 9.877 9e-05 | -2.258 4e-06 | 8.121 7e-05 |
| K2 | -2.048 4e-07 | -2.078 7e-07 | -6.927 5e-07 |
| K3 | 9.532 2e-011 | 1.947 0e-09 | 1.231 3e-09 |
| P1 | 1.419 3e-05 | 2.825 3e-04 | 3.501 9e-05 |
| P2 | -7.217 2e-06 | 9.810 3e-05 | -6.258 1e-06 |
| B1 | -2.636 3e-04 | -1.038 9e-07 | -9.087 0e-05 |
| B2 | -1.190 0e-05 | 2.796 3e-08 | 2.116 2e-06 |
试验测区位于辽宁工程技术大学北校区,如图 1所示。测区地形类型为平原,测区面积约为1.1 km2,摄影比例尺为1:2000。沿东西方向敷设4条测图航线。测区按规范布设了12个平高控制点,测区内部大致均匀布设了15个平高检查点。

|
| 图 1 测区全景图 |
获取不同的相机镜头畸变参数后,分别研究了通过不同的畸变参数组合条件下的像点量测精度。方案0为不含任何畸变参数的组合;方案1为只包含K1的模型;方案2为只包含K2的模型;方案3为包含K1和K2的组合模型;方案4为包含K1、K2、K3的组合模型;方案5相比方案4增加了P1和P2;方案6相对于方案5增加了B1和B2。
2.2 结果分析对不同方案,采用Virtuozo AAT-PATB空三加密软件进行了平差计算,并分别统计了其像点的量测精度的单位权中误差。先后采用佳能25 mm、索尼16 mm、佳能35 mm镜头进行航测影像采集,经过处理后像点的量测精度统计见表 2,统计项包含单位权中误差Sigma、像点坐标 (x, y) 的中误差 (RMSx, RMSy)。
| μm | |||||||||||
| 方案 | 佳能25mm镜头 | 索尼16mm镜头 | 佳能35mm镜头 | ||||||||
| Sigma | RMSx | RMSy | Sigma | RMSx | RMSy | Sigma | RMSx | RMSy | |||
| 方案0 | 9.72 | 5.28 | 5.97 | 8.67 | 4.86 | 4.93 | 12.21 | 6.97 | 7.23 | ||
| 方案1 | 9.06 | 4.90 | 5.56 | 8.12 | 4.57 | 4.62 | 11.58 | 6.47 | 6.82 | ||
| 方案2 | 未收敛 | 未收敛 | 未收敛 | 8.23 | 4.61 | 4.73 | 未收敛 | 未收敛 | 未收敛 | ||
| 方案3 | 5.23 | 3.11 | 2.90 | 4.75 | 2.69 | 2.44 | 6.86 | 4.48 | 4.49 | ||
| 方案4 | 5.09 | 2.98 | 2.92 | 4.59 | 2.53 | 2.43 | 6.79 | 4.36 | 4.48 | ||
| 方案5 | 5.04 | 2.97 | 2.87 | 4.33 | 2.50 | 2.36 | 6.72 | 4.34 | 4.42 | ||
| 方案6 | 5.03 | 2.96 | 2.85 | 4.31 | 2.50 | 2.35 | 6.71 | 4.33 | 4.40 | ||
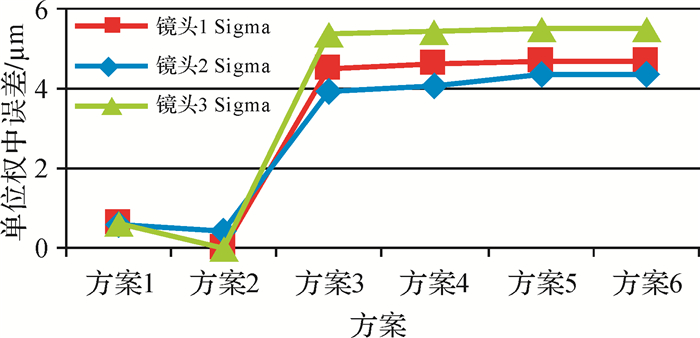
综合上述3组平差统计结果可以得到其他方案相对方案0的精度提升情况,未收敛的值视为与不进行纠正的情况精度一致。图 2为不同组合方案相对于方案0时的单位权中误差。
|
| 图 2 3种镜头的单位权中误差 |
由图 2可得,3种镜头的试验结果中,相对于不进行任何畸变纠正的方案,方案1的单位权中误差平均提升0.61 μm;方案2中存在两个不收敛情况,说明仅考虑K2的方案效果较差;方案3的单位权中误差平均提升4.59 μm,提升效果明显;方案4的单位权中误差平均提升4.71 μm;方案5的单位权中误差平均提升4.84 μm;方案6的单位权中误差平均提升4.85 μm。可见,随着方案中畸变参数的增加,单位权中误差精度也随之提高。但是相对于其他方案,仅考虑K1和K2的方案3的精度提升最为明显,当将全部畸变参数参与计算时,精度最高。
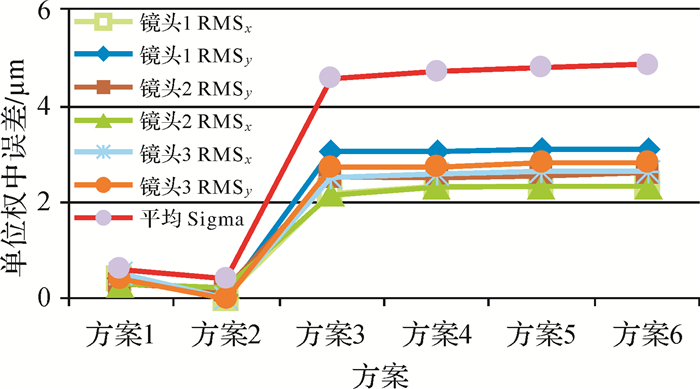
图 3为相对于方案0的情况下,其他方案的点位量测精度提升情况。
|
| 图 3 3种镜头的像点量测精度 |
由图 3可得,3种镜头的情况下,相对于方案0,其他畸变纠正方案下的像点量测精度均有不同程度的提升。方案1的像点量测精度分别提升了0.39和0.38 μm,与单位权中误差类似;方案2中存在两组不收敛的情况,因此说明只考虑畸变K2的模型效果较差;方案3与之前的两个方案相比在精度上有明显提升,x和y方向分别提升2.28和2.77 μm;方案4的结果中,x和y方向分别提升2.41和2.77 μm;方案5结果中,x和y方向分别提升2.43和2.83 μm;方案6结果中,x和y方向分别提升2.44和2.84 μm。此外,各种方案的点位量测精度提升情况与单位权中误差的趋势大致相同。可见,与单位权中误差类似,随着方案中畸变参数的增加,像点量测精度也随之提高。特别是仅考虑K1和K2的方案3的精度提升最为明显,当增加全部的畸变参数参与计算时,精度最高。
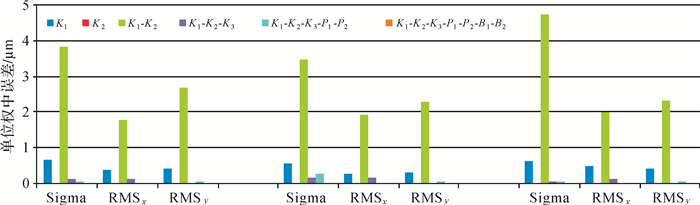
图 4为3种镜头情况下,各方案相对于前一方案的单位权中误差及点位量测中误差的变化量。
|
| 图 4 不同组合模型下相对提高的精度 |
由图 4可得,3种情况下,与前一方案相比,当采用K1纠正时,精度有一定程度的提升;当采用K2纠正时,存在不收敛情况,精度可能不会提升;方案3采用了K1和K2组合,精度提升最为明显,单位权中误差提升了4.01 μm,像点量测误差平均提升精度为2.16 μm;后续方案中逐渐增加了K3、P1、P2和B1、B2,但精度提升都不明显,单位权中误差分别提升了0.12、0.13和0.01 μm,像点量测误差平均提升精度为0.07、0.04和0.01 μm。综合上述数据,可以分析得出:①对于低空无人机测绘,采用适宜的模型和准确的方法事先检测无人机相机畸变差参数十分重要,对像点量测精度影响深远,有条件的情况下尽可能采用完整的畸变差模型对像点进行系统误差改正,能有效提高空三精度;②径向畸变差是无人机相机镜头畸变差中主要误差,对最终像点量测精度的影响最大,切向畸变差和面阵内变形较小;③径向畸变差中单独采用K1或K2时,纠正的效果有限,而整体使用K1和K2组合时,精度提升效果非常明显,而再增加K3、P1、P2、B1、B2后的精度提高不明显,因此,当纠正条件有限时,优先考虑K1和K2组合的模型。
3 结语无人机航测已经成为测绘领域中常用的技术手段,而镜头的畸变需要测定和修正才能够满足各种测图的需求。镜头的畸变参数一般包括径向畸变、切向畸变差和非方形像元改正。由于各种相机镜头的畸变参差不齐,需要事先测定各种畸变参数。但是在有些条件下,只能获取镜头的部分畸变参数,无法得到全部的畸变参数,为此,本文研究了各种畸变参数组合对航测结果精度的影响。通过采用3种不同型号的镜头对试验区进行无人机航测,并采用Virtuozo AAT-PATB空三软件进行了结果处理。试验结果表明,畸变参数越全面,最终结果的精度越高。各种模型情况下,单独纠正任意一个参数得到的结果都不是非常理想,而采用K1和K2组合的情况下,航测结果的精度可以得到显著的提升,因此,条件有限的情况下,采用K1和K2组合的模型最为实用。本文的结论可以为无人机航测提供必要的参考。
| [1] | 吴博义, 苏国中. 低空大比例尺地形图航测生产关键技术[J]. 测绘科学, 2016, 41 (8) : 1–11. |
| [2] | 林宗坚, 解斐斐, 苏国中. 宽角相机低空航测的精度分析[J]. 测绘学报, 2014, 43 (10) : 991–997. |
| [3] | 李畅. 利用灭点进行相机检校与定姿的充要条件及其不确定性分析[J]. 测绘学报, 2012, 41 (6) : 851–856. |
| [4] | 张惠均. 无人机航测带状地形图的试验及分析[J]. 测绘科学, 2013, 38 (3) : 100–102. |
| [5] | 魏方震, 武少丰, 吉世鹏, 等. 天宝UX5无人机航测系统在公路勘察设计中的应用[J]. 测绘通报, 2015 (3) : 138–139. |
| [6] | 刘力荣, 左建章, 关艳玲. POS辅助航空摄影测量精度分析[J]. 测绘科学, 2012, 37 (4) : 197–199. |
| [7] | 唐健林. 机载定位定姿辅助空中三角测量成图精度分析[J]. 测绘科学, 2014, 39 (10) : 61–63. |
| [8] | 黄健, 邹学忠. 辅助定向法空中三角测量区域网布控方案分析[J]. 测绘通报, 2014 (7) : 70–74. |
| [9] | 蒋春华. 利用A3数码航摄仪进行复杂地形控制点布设的研究[J]. 测绘通报, 2015 (5) : 84–86. |
| [10] | 陈良浩, 朱彩英, 徐青, 等. 无人机航测水域控制点布设方案的精度试验[J]. 测绘科学, 2016, 41 (7) : 205–210. |
| [11] | 程效军, 胡敏捷. 数字相机畸变差的检测[J]. 测绘学报, 2002, 31 (S1) : 113–117. |
| [12] | 崔红霞, 孙杰, 林宗坚, 等. 非量测数码相机的畸变差检测研究[J]. 测绘科学, 2005, 30 (1) : 105–107. |
| [13] | 李海滨, 郝向阳. 一种基于基本矩阵的相机畸变差自动校正方法[J]. 中国图象图形学报, 2008, 13 (11) : 2081–2086. DOI:10.11834/jig.20081104 |
| [14] | 崔瑞兵, 靳国旺, 刘辉, 等. 利用线性变换和后方交会的月球车相机标定[J]. 测绘科学, 2016, 41 (7) : 131–137. |
| [15] | 张烁, 燕丹晨, 甄莹, 等. 利用线性变换和后方交会的月球车相机标定[J]. 测绘科学, 2015, 40 (11) : 29–33. |


