2. 北斗导航应用技术河南省协同创新中心,河南 郑州 450001;
3. 华南师范大学,广东 广州 510000
2. BeiDou Navigation Technology Collaborative Innovation Center of Henan, Zhengzhou 450001, China;
3. South China Normal University, Guangzhou 510000, China
目前在三频模糊度解算方法中以TCAR和CIR方法为代表,两种方法的实质是等价的,均是根据不同组合观测值的波长及其误差特点采用简单的逐级取整固定模糊度[1-2]。短基线情形下,两种方法都可以较高的成功率固定模糊度。然而对于中长基线而言,残留系统误差的影响导致宽巷及窄巷模糊度难以固定。为了改进TCAR算法,不同学者进行了大量的研究,文献[3]利用电离层延迟改正后的窄巷观测值进行模糊度固定来提高成功率,文献[4]提出利用模糊度固定后的两个超宽项与一个窄巷组合构成无几何无电离层组合。但是这些方法都会放大观测噪声且大部分基于仿真数据,实际效果并不太理想,如何寻找较优的新方法进行中长基线模糊度快速解算仍然值得研究。
本文拟分析双差电离层残差对经典TCAR算法中宽巷及窄巷模糊度固定成功率的影响,提出一种新的无几何无电离层模糊度解算方法,通过对伪距观测值赋予不同的权重来辅助宽巷及窄巷模糊度求解;然后再通过多历元平滑获取宽巷及窄巷模糊度值,实现中长基线模糊度快速固定。通过实测BDS三频数据算例分析,相比经典TCAR算法,该方法可大大改善模糊度的求解精度。
1 三频组合观测量理论不失一般性,假设3个载波频率依次为f1、f2、f3,分别对应北斗B1、B2、B3,则线性组合的方程可以描述为[5]
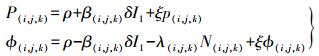 (1)
(1) 式中,β(i, j, k)代表组合观测值以f1频点电离层延迟为参照的电离层放大因子
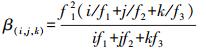 (3)
(3) 另外ξp(i, j, k)、ξφ(i, j, k)代表伪距、载波各自线性组合的观测噪声 (包含了残留多路径和高阶电离层延迟的影响)。假定伪距3个频点的观测噪声相互独立且标准差相同,即σP1=σP2=σP3=σP,同样假定载波3个频点σφ1=σφ2=σφ3=σφ,则组合观测值噪声方差可表示为[6]
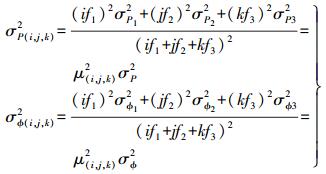 (4)
(4) 式中,μ(i, j, k)代表噪声放大因子,即
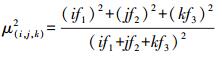 (5)
(5) 由于三频最优组合理论已经被许多学者采用不同的方法进行了大量研究,参照已有文献,本文直接筛选出超宽巷、宽巷、窄巷组合见表 1[7]。
| φ(i, j, k) | λ(i, j, k) | β(i, j, k) | μ(i, j, k) |
| φ(0, -1, 1) | 4.884 | -1.592 | 28.529 |
| φ(1, 0, -1) | 1.025 | -1.231 | -1.232 |
| φ(0, 1, 0) | 0.248 | 1.672 | 1.0 |
经典的TCAR/CAR算法均是采用多频伪距和相位组合观测值消除几何误差的模糊度求解模型。为了便于分析,按照上文筛选的超宽巷、宽巷、窄巷组合为例,则传统三频模糊度的计算流程如下[8](实际分步求解时电离层延迟、观测噪声均忽略直接取整固定,为便于分析,人为添加):
(1) 固定超宽巷模糊度 (EWL) 为
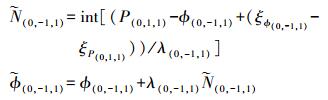 (6)
(6) (2) 固定宽巷模糊度 (WL) 为
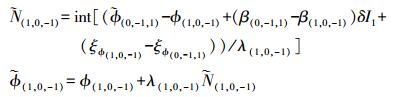 (7)
(7) (3) 固定窄巷模糊度 (NL) 为
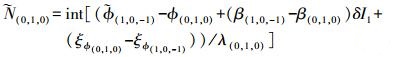 (8)
(8) 由式 (3)—式 (8),根据误差传播定律,超宽巷、宽巷、窄巷模糊度浮点解的精度 (顾及电离层及观测噪声,以周为单位) 分别如下
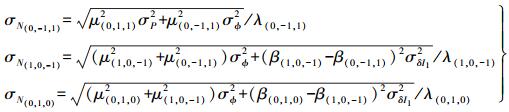 (9)
(9) 超宽巷的解算组合实际上是一个无几何无电离层组合,只受观测噪声的影响[9];而宽巷、窄巷的解算仅仅是一个无几何组合,没有消除电离层的影响。可以假定观测噪声服从正态分布,则超宽巷、宽巷、窄巷浮点模糊度服从的分布分别为
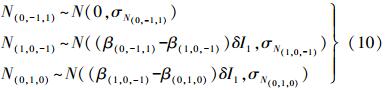 (10)
(10) 根据文献[2], 在给定电离层延迟大小及观测噪声条件下,可以根据下式计算每一步的模糊度固定成功率,即
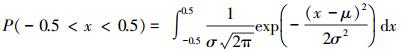 (11)
(11) 式中,x表示模糊度浮点解与相应真值的差值;μ和σ分别表示x的均值和标准差 (以周为单位,且假定σφ=0.4 cm,σP=60 cm)。
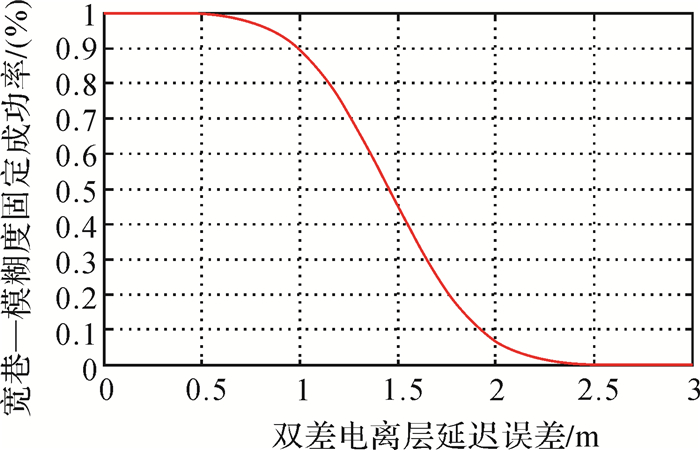
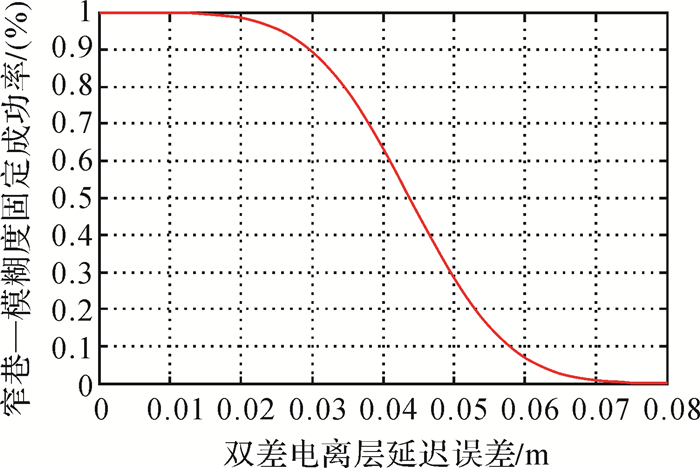
对于超宽巷,由于其波长远大于观测噪声,基线的长短对其影响不大,均能可靠固定。然而对于宽巷与窄巷而言,短基线之间的电离层延迟相关性比较强,双差之后可以忽略直接取整固定,但对于长基线,由于电离层延迟相关性减弱,双差之后难以消除,导致其固定成功率降低[10]。通过图 1与图 2可以看出,对于宽巷,当电离层残差δI1 < 1 m时,宽巷固定成功率大于90%,1 m < δI1 < 2.5 m时,成功率快速降低;电离层延迟对窄巷的影响更大,当δI1 < 0.035 m时,窄巷模糊度成功率不低于90%,当δI1 > 0.07 m时,成功率基本为0。而在实际应用中,电离层延迟很容易超过0.07 m,因此为了提高三频模糊度的解算性能,必须想办法消除或减弱双差电离层残差的影响。
|
| 图 1 双差电离层延迟对宽巷模糊度固定成功率的影响 |
|
| 图 2 双差电离层延迟对窄巷模糊度固定成功率的影响 |
由上文的分析可知,双差电离层延迟是影响经典TCAR算法中宽巷与窄巷模糊度固定的关键因素,尤其窄巷模糊度的求解甚至要求双差电离层延迟限制在厘米级。为了提高宽巷、窄巷模糊度固定成功率,必须消除或减弱双差电离层残差的影响[11]。为此,本文提出了一种新方法,把3个原始伪距观测量与已经固定的超宽巷 (EWL) 应用于宽巷的求解中;同理,把已经固定的超宽巷 (EWL)、宽巷 (WL) 及3个原始伪距观测量应用于窄巷的求解中。
对宽巷、窄巷求解过程中的各辅助添加量要赋予不同的权重系数,系数的选取要同时满足无几何、无电离层及最小观测噪声3个条件。
(1) 宽巷模糊度固定为
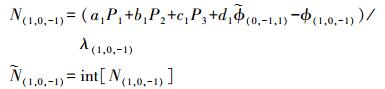 (12)
(12) 式中,权重系数a1、b1、c1、d1满足以下条件:
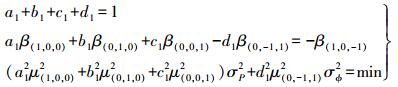 (13)
(13) 根据式 (13) 检索出的最优权重系数见表 2。
由上文的分析可知,修改后的宽巷模糊度的固定组合是一个无几何无电离层组合,消除了双差电离层残差的影响,仅受观测噪声的影响,可以假定宽巷模糊度浮点解服从零均值的正态分布,即
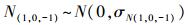 (14)
(14) 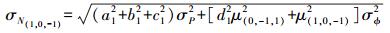 (15)
(15) 根据式 (15) 可以计算宽巷模糊度的估值标准差为0.353 3周,且不受电离层残差的影响,因此可以实现单历元模糊度的固定。
(2) 窄巷模糊度的固定为
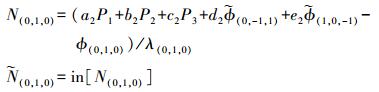 (16)
(16) 式中,权重系数a2、b2、c2、, d2、e2满足以下条件
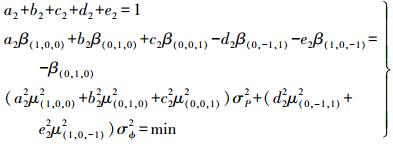 (17)
(17) 根据式 (17) 检索出的最优权重系数见表 3。
修改后的窄巷模糊度的固定组合同样是一个无几何无电离层组合,消除了双差电离层残差的影响,仅受观测噪声的影响,同样可以假定窄巷模糊度浮点解服从零均值的正态分布,即
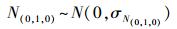 (18)
(18) 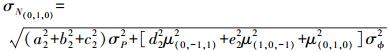 (19)
(19) 根据式 (19) 可以计算窄巷模糊度的估值标准差为3.557 7周,导致该窄巷模糊度不可以实现单历元模糊度的固定,但是该窄巷模糊度的求解有效消除了电离层残差的影响,几乎不受基线长度的限制,只受观测噪声的影响,而观测噪声是可以通过多历元数据的平滑来减弱的。因此可以通过多历元数据平滑取整来求解窄巷模糊度,求解公式如下
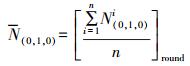 (20)
(20) 利用上海司南测量型接收机 (M300Pro) 于2016年5月18日在长沙与郑州之间采集了一组北斗三频静态长基线数据 (730 km/10 s/2.5 h),为了验证本文提出的新算法,采集数据时设置高度角为20°,以消除多路径的影响。另外,使用LAMBDA方法多历元连续搜索确定的模糊度作为参考值[12-13],进而统计了几个卫星对的宽巷、窄巷浮点解模糊度残差值,最后对浮点解多历元平滑进而求解模糊度。
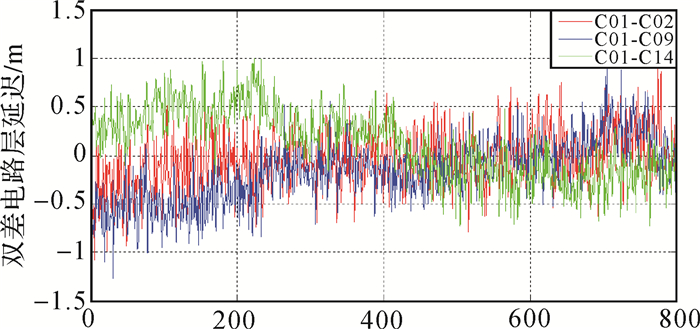
利用已经固定的超宽巷、窄巷组合可以反求出各个卫星对的双差电离层延迟误差δI1, 如图 3所示,列出了C01-C02、C01-C09、C01-C14 3组卫星对的双差电离层延迟,可以看出基本所有历元满足δI1 < 1 m。由上文分析可知,经典TCAR模式下,宽巷模糊度的求解成功率不小于90%,但δI1 < 0.07 m的要求很难满足,因此采用传统无几何三频模糊度方法,窄巷模糊度基本不能固定。下面列出了利用本文提出的新算法的解算结果。
|
| 图 3 双差电离层延迟误差 |
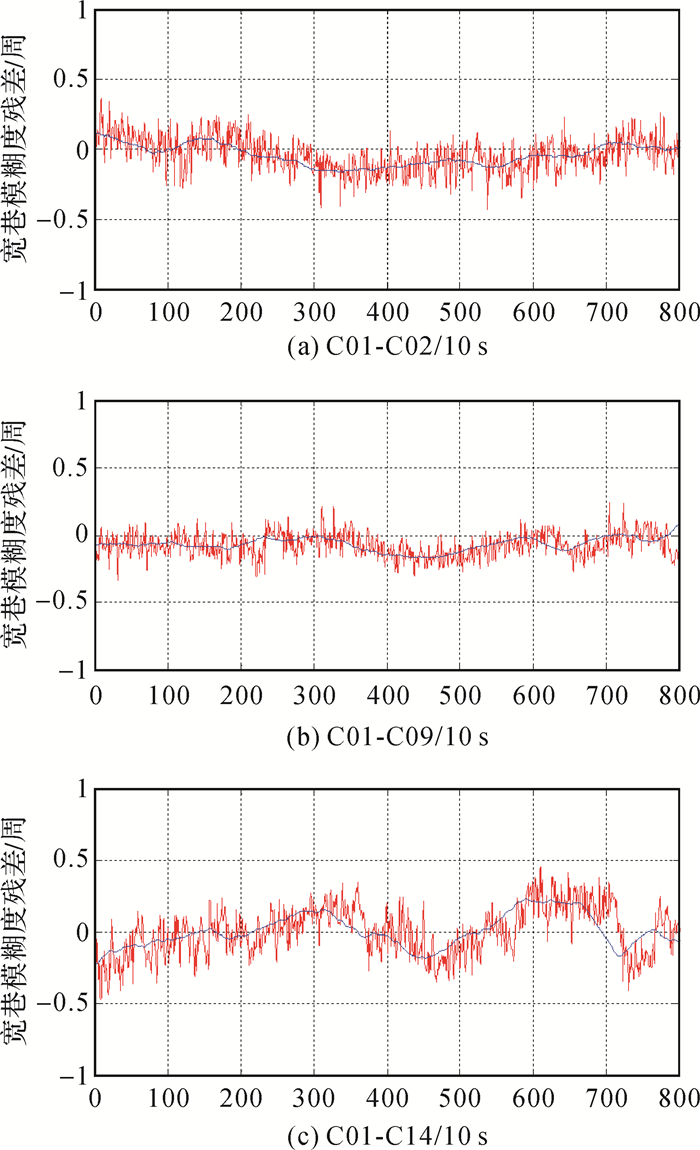
由图 4可以看出,所有历元的宽巷模糊度残差均小于0.05周,经过数据平滑后均可以可靠固定 (限于篇幅, 本文只列取了卫星C01-C02、C01-C09、C01-C14的宽窄巷模糊度估值残差及平滑序列图)。
|
| 图 4 宽巷模糊度估值误差及平滑序列图 |
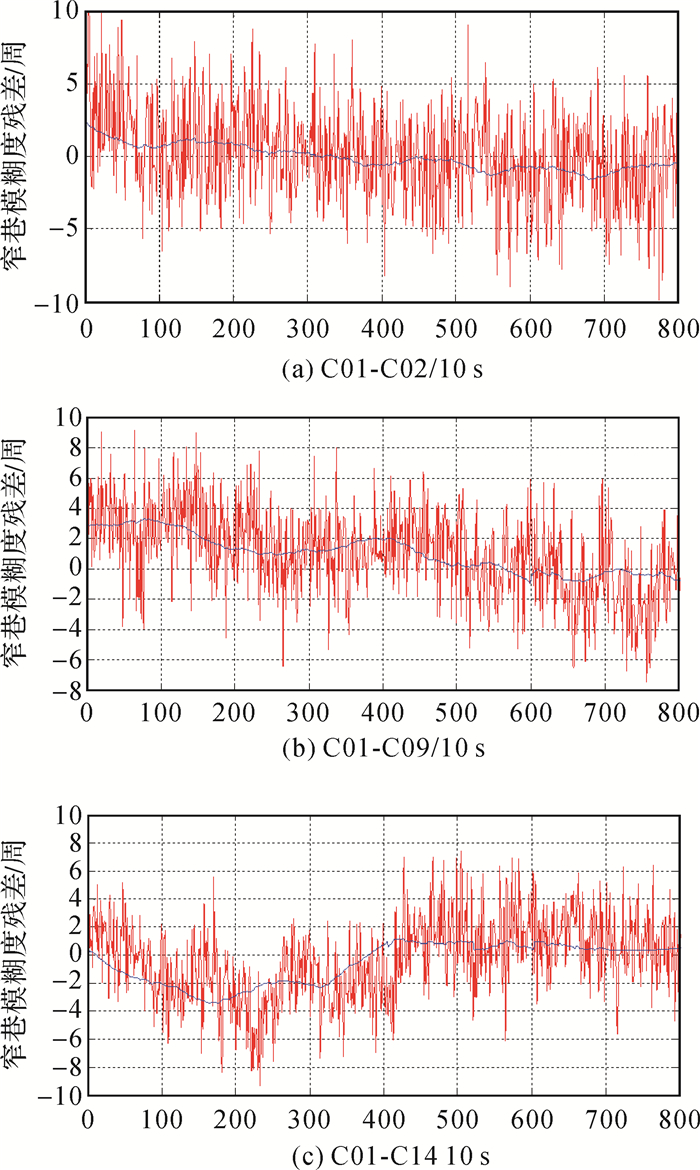
图 5为窄巷模糊度估值误差及平滑序列图。可以看出,窄巷浮点解的估值残差基本都在10周以内,经过多历元数据平滑消噪后逐步收敛 (不同卫星对的收敛时间有所区别),最终控制在1~2周的范围内。对于取整得到的2个模糊度还需要进一步验证,且无几何无电离层组合基本与距离无关。由此可以看出,该方法经过数据平滑消噪可以实现中长基线模糊度的快速解算。
|
| 图 5 窄巷模糊度估值误差及平滑序列图 |
本文通过优选三频观测量组合,分析了双差电离层残差对经典TCAR算法中宽巷及窄巷模糊度固定成功率的影响,提出了一种新的无几何无电离层模糊度解算方法,应用于中长基线模糊度快速解算。通过实测BDS三频数据验证了本文提出观点的正确性和新方法的有效性,得出以下结论:
(1) 双差电离层延迟对中长基线宽巷、窄巷,尤其是窄巷模糊度固定成功率影响非常大,这也是经典TCAR算法不能胜任长基线解算的主要原因。
(2) 相比经典TCAR算法,本文方法可大大改善中长基线模糊度的求解精度,经过数据平滑并验证基本可以实现中长基线模糊度的快速解算。
需要指出的是,由于本文采取的是引进伪距辅助量的无几何无电离层弱观测噪声组合,虽然消除了电离层延迟影响,但引进的伪距辅助观测量会放大多路径误差的影响[14],而多路径误差很难通过双差来消除,进而会降低窄巷模糊度求解的可靠性[15],这也是该算法需要进一步优化的地方,以期得到更可靠的解算结果。
| [1] | TEUNISSEN P J G. Least-squares Estimation of the Integer GPS Ambiguity[C]//Delft Geodetic Computing Centre (LGR), Section IV: Theory and Methodology. Beijing: IAG General Meeting Beijing, 1993. |
| [2] | FENG Yanming. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-reduced Virtual Signals[J]. Journal of Geodesy, 2008, 82(12): 847–862. DOI:10.1007/s00190-008-0209-x |
| [3] | 伍岳, 付小林, 李海军, 等. TCAR/MCAR方法在不同距离基线模糊度求解中的应用[J]. 武汉大学学报 (信息科学版), 2007, 32 (2) : 172–175. |
| [4] | 李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38 (4) : 296–301. |
| [5] | TANG Weiming, DENG Chenlong, SHI Chuang, et al. Triple-frequency Carrier Ambiguity Resolution for BeiDou Navigation Satellite System[J]. GPS Solution, 2014, 18(3): 335–344. DOI:10.1007/s10291-013-0333-9 |
| [6] | ZHANG Xiaohong, HE Xiyang. Performance Analysis of Triple-frequency Ambiguity Resolution with BeiDou Observations[J]. GPS Solution, 2016, 20(2): 269–281. DOI:10.1007/s10291-014-0434-0 |
| [7] | 李金龙, 杨元喜, 何海波, 等. 函数极值法求解三频GNSS最优载波相位组合观测量[J]. 测绘学报, 2012, 41 (6) : 797–803. |
| [8] | YE Shirong, CHEN Dezhong, LIU Yanyan, et al. Carrier Phase Multipath Mitigation for BeiDou Navigation Satellite System[J]. GPS Solutions, 2014. DOI:10.1007/s10291-014-0409-1 |
| [9] | 黄令勇. GNSS多频数据处理理论与方法研究[M]. 郑州: 信息工程大学, 2012. |
| [10] | URQUHART L. An Analysis of Multi-frequency Carrier Phase Linear Combinations for GNSS[M]. Canada: University of New Brunswick, 2000. |
| [11] | ZHAO Qile, DAI Zhiqiang, HU Zhigang, et al. Three-carrier Ambiguity Resolution Using the Modified TCAR Method[J]. GPS Solution, 2014, 18(4): 589–599. |
| [12] | 冯来平. GPS多频观测数据处理方法及应用研究[D].郑州:信息工程大学, 2009. |
| [13] | WU Xiaoli, ZHOU Jianhua, WANG Gang, et al. Multipath Error Detection and Correction for GEO/IGSO Satellite[J]. Science China, Physics, Mechanics & Astronomy, 2012, 55(7): 1297–1306. |
| [14] | 黄令勇, 宁德阳, 吕志平, 等. 两种长基线模糊度解算方法在北斗三频应用中的比较[J]. 大地测量与地球动力学, 2014, 34 (5) : 101–105. |
| [15] | MORADI R, SCHUSTER W. The Carrier-multipath Observable: A New Carrier-phase Multipath Mitigation Technique[J]. GPS Solution, 2015, 19(1): 73–82. DOI:10.1007/s10291-014-0366-8 |


