2. 上海华测导航技术有限公司,上海 201702
2. Shanghai China Navigation Technology Co., Ltd., Shanghai 201702, China
全球卫星导航定位系统 (global navigation satellite system, GNSS),目前泛指美国的GPS、俄罗斯的GLONASS、欧盟的Galileo及中国的BDS。目前建立的GNSS变形监控在线实时分析系统广泛应用于大坝、大型桥梁、高层建 (构) 筑物、滑坡和地区性地壳变形监测。如我国在青江隔河岩大坝建立的GPS自动化变形监测系统,由数据采集、数据传输、数据处理与分析3大部分组成。实践证明,采用一机多天线GPS系统,不仅可大大节省硬件设备费用的投入,而且能够有效地应用于滑坡和大坝等局部变形监测[1]。为此研究建立技术先进而又实用的GNSS变形监控在线实时分析系统是一个重要的发展趋势。然而,由于美国的GPS政策,出于保护美国信息安全的需要,美国军方对GPS发布的民用信号所进行的不定期短暂干扰而经常出现RTK失锁现象,大大降低了测量精度,并导致可能会出现在某个关键时刻 (如台风、地震、船撞等) 监测不到数据的现象[2]。而GLONASS系统采用频分多址的方式调制卫星信号,不同卫星的频率不同,这给模糊度的固定造成了一定困难[3-4]。
基于上述GPS和GLONASS系统的缺陷,文献[5]利用GPS/GLONASS组合定位验证了上述方法在变形监测中的有效性。本文在分析监测系统各种误差的基础上,出于对项目和对数据的保密性,以某露天煤矿排土场边坡GNSS变形监测项目为例,在设计变形监测系统的基础上,利用华测HCMonitor变形监测系统专用软件,对监测数据采用不同卫星监测系统数据进行组合定位,分析和对比解算数据,探讨北斗卫星导航系统 (BDS) 的应用效果并提出合理的建议。
1 北斗监测系统工作原理 1.1 北斗卫星导航系统定位原理BDS是中国正在实施的自主发展、独立运行的全球卫星导航系统。目前的卫星定位系统在进行定位测量时,不论是测码伪距绝对定位还是测相伪距绝对定位,由于卫星星历误差、接收机钟与卫星钟同步差、大气折射误差等各种误差的影响,导致定位精度较低。
相对定位是用两台GPS接收机,分别安置在基线的两端,同步观测相同的GPS卫星,通过两测站同步采集GPS数据,经过数据处理以确定基线两端点的相对位置或基线向量, 故相对定位有时也称为基线测量。这种方法可以推广到多台GPS接收机安置在若干条基线的端点,通过同步观测相同的GPS卫星,以确定多条基线向量。相对定位中,需要在多个测站中至少以一个测站的坐标值作为基准,利用观测出的基线向量,去求解出其他各站点的坐标值。
1.2 变形监测点的数据处理目前变形监测的基线向量解算模式可分为独立解算模式和相关解算模式。
1.2.1 独立解算模式独立解算模式对基线进行逐条解算,每次解算仅包含一条基线向量结果。换言之,一次仅提取基准点和一个测点的同步观测数据,并通过站星际双差模型求解它们之间形成的基线向量。当某时段进行了多个测点同步观测,而需要求解多条基准-测点基线向量时,则需要将基准点与各个测点分别形成双差模型,独立解算各基线向量。然而,解算的结果无法反映同步观测基线向量间的统计相关性。另外,单个基线向量独立求解,无法利用待定参数的关联性与观测数据的共享性。其优点是:平差数学模型简单、估计参数较少、数据处理响应速度快。因此,在工程实践中,普遍采用独立解算模式,绝大多数商业软件也采用该模式进行基线解算。
1.2.2 相关解算模式相关解算模式对独立基线进行逐时段解算,每解算包含n条基线向量的结果。换言之,一次提取基准点和n个测点的同步观测数据、解算过程中,求解出n条相互函数独立的基线向量。且可反映同步基线向量之间的统计相关性。但是,相关解算模式的平差数学模型及解算过程交复杂,数据处理响应速度较慢。因此,仅在高精度应用中采用相关解算模式,绝大多数科学软件也采用该模式进行基线解算[6]。
2 边坡监测系统的监测体系设计根据某露天采矿场和排土场边坡稳定性现状及未来采矿工程发展需要,在矿山南部采区和西部采区重点部位,建立边坡自动监测与预警系统,对边坡变形动态进行监测。系统包括参考站1个、连续监测站18个、系统制软件1套。
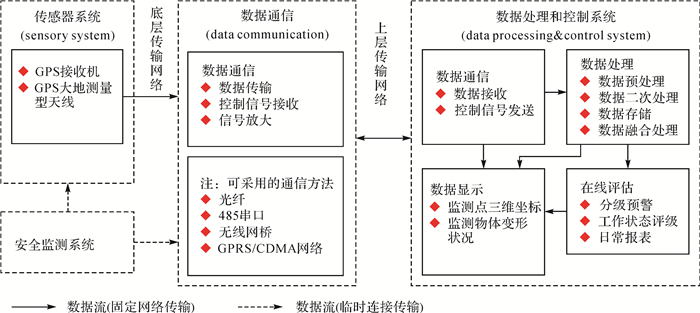
边坡监测系统由传感器系统单元、数据通信单元、数据处理与控制单元 (HCmonitor软件部分、HCmas平台软件)、避雷系统、预警系统等各个分部组成,如图 1所示。
|
| 图 1 GNSS变形监测系统总体框架 |
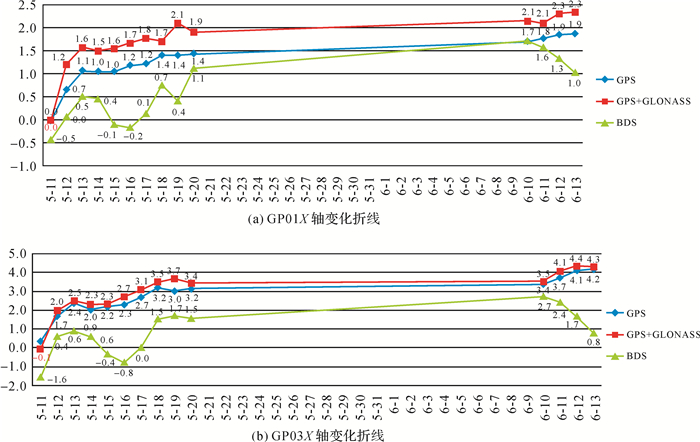
出于项目保密需要,使用数据受限,项目选取参考站1个 (GP02)、监测站2个 (GP01、GP03),课题组根据2015年5月10日至2015年6月13日 (15天) 的监测数据分别提取了GPS、GPS+GLONASS和BDS三组卫星定位数据。以5月10日作为起始数据,利用HCmonitor软件每天按5个时段 (2h),分别解算出每个时段的空间三个坐标方向的相对累计变化量,同时计算出每天的平均累计变化量。最后利用Excel软件画出三坐标轴方向的变化折线图 (如图 2—图 4所示)。
|
| 图 2 |
|
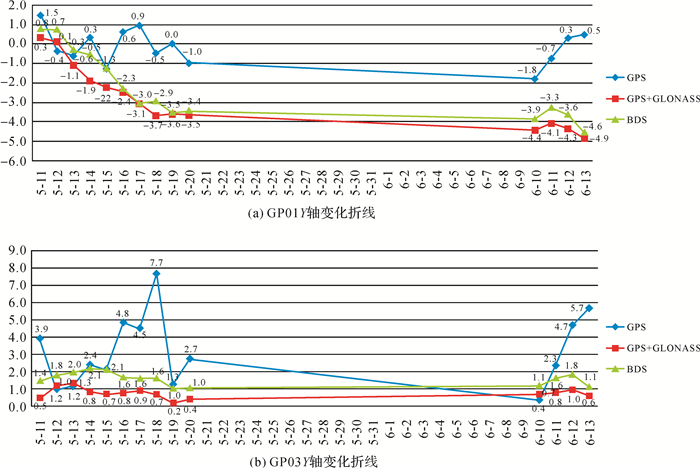
| 图 3 |
|
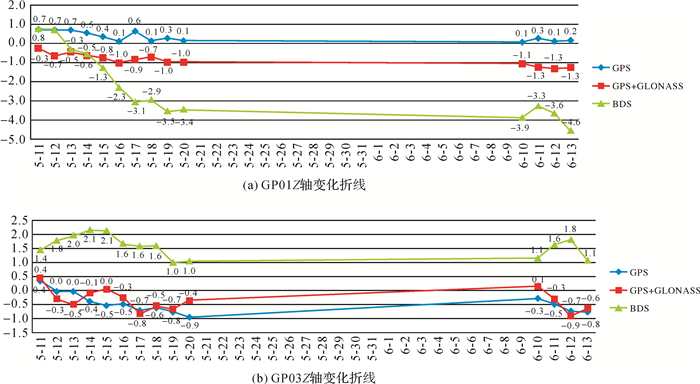
| 图 4 |
空间位置定位结果的精度取决于卫星空间分布,即其空间定位的图形精度GDOP因子。在不考虑BDS系统的前提下,从卫星定位的原理分析,一般认为GPS+GLONASS双系统的监测结果为最佳的可靠成果。结合图 2(a)、(b) X轴方向的变化情况分析可以看出,对比BDS系统、GPS系统和GPS+GLONASS双系统的监测数据解算结果,点的位移变化趋势一致。最大的位移量为GPS系统,最小的位移量为BDS系统,GPS+GLONASS双系统的监测结果位于上述两单系统的中间。BDS系统X轴方向位移监测数据值比GPS系统、GPS+GLONASS双系统的监测结果均偏小。通过对为期15天的监测数据分析,BDS系统和GPS+GLONASS双系统最大差值GPS01点仅为1.8 mm,GPS03点仅为3.6 mm。
Y轴方向的变化情况如图 3(a)、(b) 所示,最大的位移量为GPS系统,最小的位移量为GPS+GLONASS双系统,BDS系统的监测结果位于上述两系统的中间。BDS系统的监测结果比GPS系统偏小,比GPS+GLONASS双系统偏大。BDS系统与GPS+GLONASS双系统最大差值GPS01点仅为1.3 mm;GPS03点仅为1.4 mm。
Z轴方向的变化情况如图 4(a)、(b) 所示,BDS系统的监测结果出现的情况随点的位置不同而不同,没有规律可言。但BDS系统的监测结果和GPS+GLONASS双系统监测结果差值不大。BDS和GPS+GLONASS双系统最大差值GPS01点仅为3.3 mm;GPS03点仅为2.7 mm。
依据《工程测量规范》(GB 50026—2007) 变形监测的等级划分和精度要求,水平位移监测变形观测点的中误差规定:一等1.5 mm;二等3.0 mm;三等6.0 mm;四等12.0 mm。根据误差传播定律,平面位置中误差可分解为X和Y方向的位移中误差,二等X和Y方向位移中误差分别为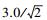
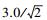
(1) BDS系统X轴方向位移监测数据值比GPS系统、GPS+GLONASS双系统的监测结果均偏小;BDS系统Y轴方向位移的监测结果位于GPS系统结和GPS+GLONASS双系统的监测结果中间,BDS的监测数结果比GPS系统结果偏小、比GPS+GLONASS双系统的监测结果偏大;BDS系统Z轴方向位移变化情况,随点的位置不同而不同,没有规律可言。但BDS系统的监测结果和GPS+GLONASS双系统监测结果差值不大。
(2) 目前,BDS系统只覆盖亚太地区,一旦卫星的数量达到全球覆盖,北斗系统完全可以取代GPS系统和GLONASS系统。
(3) 研制BDS接收机产品的费用比三星系统的费用成本要低,从而用于监测的成本和总费用随之也下降,使卫星定位监测技术到达普及。
(4) 开发更加严密的BDS系统的解算软件,以便消除卫星定位测量的各项误差,从而提高变形监测的精度。
| [1] | 马琴. 基于GPS在变形监测中应用的研究[J]. 测绘技术装备, 2014 (2) : 25–26. |
| [2] | 邵伯兴, 彭家意. 润扬长江公路大桥GPS+北斗变形监测系统应用探索[J]. 现代交通技术, 2014, 11 (4) : 32–34. |
| [3] | 裴霄.GPS/GLONASS组合定位[D].上海:同济大学, 2013. |
| [4] | 高星伟, 葛茂荣, 李毓麟. GLONASS浮点解的解算方法与实验[J]. 全球定位系统, 2000, 25 (1) : 22–24. |
| [5] | 王建, 余代俊, 戴继红. GPS/GLONASS组合定位及其在变形监测中的应用[J]. 工程勘察, 2014, 42 (2) : 78–81. |
| [6] | 刘志平. GNSS边坡监测与变形分析[M]. 北京: 测绘出版社, 2014. |
| [7] | 周在明, 许德伟, 陈本清. 河口海岸区GPS高程异常的空间特征与拟合研究[J]. 测绘科学, 2014, 39 (12) : 36–39. |
| [8] | 熊春宝, 田力耘, 叶作安, 等. GNSS RTK技术下超高层结构的动态变形监测[J]. 测绘通报, 2015, 7 : 14–17. |
| [9] | 邹进贵, 李勇. GNSS天线阵列接收机数据采集与解码的实现及应用[J]. 测绘通报, 2015 (8) : 1–3. |
| [10] | 陈振, 秘金钟, 王权, 等. BDS/GPS实时动态网络伪距差分定位[J]. 测绘科学, 2015, 40 (12) : 81–85. |
| [11] | 甘雨, 隋立芬, 张清华, 等. 利用时间差分载波相位的GNSS/INS紧组合导航[J]. 测绘通报, 2015 (6) : 5–8. |
| [12] | 王孟阳, 应忍冬, 刘佩林, 等. GNSS星座模拟器关键问题研究[J]. 测绘通报, 2015 (3) : 19–21. |


