粒子滤波作为一种非线性滤波算法,近年来在目标跟踪、故障诊断、测绘等方面应用越来越广泛。与传统的卡尔曼滤波相比,粒子滤波摆脱了系统线性和噪声服从高斯分布的要求,因此应用面更广,发展更迅速。
粒子滤波主要是依靠蒙特卡洛仿真法来完成一个贝叶斯递推的过程,其原理是根据上一时刻的概率生成样本集合,即为粒子。根据一定的方法调整粒子的权重和位置,用调整后的粒子来近似表示出后验概率。样本容量越大,与真实的后验概率就越接近。粒子滤波同时也存在着缺陷。滤波中重要性函数的选取将会直接影响其性能。传统滤波序贯重要性采样 (sequential importance sampling,SIS) 算法仅利用状态转移概率密度计算预测值,忽略了最新的观测值,故产生的样本并不能准确表示真实状态,最终会导致粒子退化问题。此外,序贯重要性重采样 (sequential importance resampling,SIR) 算法中的重采样步骤采用的是随机复制权值较大的粒子,使选取的粒子失去了多样性,出现粒子匮乏的现象。
为了解决粒子滤波算法中存在的缺陷,一些学者提出了改进方法。Rudolph等[1]将无迹卡尔曼滤波 (unscented Kalman filter,UKF) 融入粒子滤波中,提出了一种无迹粒子滤波 (unscented particle filter,UPF),该算法将最新观测值加入概率计算中,一定程度上改善了粒子退化问题,但其重采样过程依然存在粒子匮乏现象。Kennedy等[2]基于鸟群捕食行为的研究提出了粒子群优化算法 (particle swarm optimization,PSO)。使用该算法搜索最优粒子不仅简单易行,而且收敛速度快,同时很好地保留了粒子的多样性,避免粒子匮乏现象的发生。
本文在分析粒子滤波原理的基础上,提出了一种应用高斯粒子群优化无迹粒子滤波 (unscented particle filter using Gaussian particle swarm optimization,GPSO-UPF) 的新算法。本算法将高斯滤波器[3]引入粒子群算法中,使用高斯粒子群优化无迹粒子滤波的重采样过程,不仅能有效缓解粒子退化,提高计算效率,还能在一定程度上解决粒子匮乏问题。经过仿真试验测试,该算法不仅提高了滤波的精度,还具有很强的稳定性。
1 粒子滤波原理 1.1 贝叶斯滤波贝叶斯滤波的目的是利用系统的所有已知信息得到状态的后验概率密度。具体内容是首先利用系统模型预测状态量的先验概率密度,再引入最新的观测值进行修正,修正值即为状态量的后验概率密度。故可分为预测和更新两步。设k代表时间,xk代表系统状态,zk代表观测值。
1.1.1 预测在未得到观测值时,根据已知的系统模型与转移概率,可由k-1时刻的后验概率推导出k时刻的先验概率。即
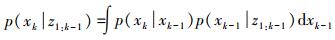 (1)
(1) 式中,p (xk-1|z1:k-1) 是k-1时刻的后验概率密度;p (xk|xk-1) 是根据系统模型得到的状态转移概率密度;p (xk|z1:k-1) 是计算得到的k时刻的先验概率密度。
1.1.2 更新根据得到的先验概率,加上观测值后,即可实现从p (xk|z1:k-1) 到p (xk|z1:k) 的推导。
具体过程是先由贝叶斯公式推导出后验概率,再由条件概率和联合分布概率公式将观测值独立出来,即
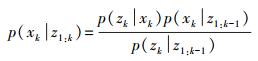 (2)
(2) 联合式 (1) 与式 (2),即可实现由k-1时刻的后验概率密度p (xk-1|z1:k-1) 到k时刻的先验概率密度p (xk|z1:k) 的推导。
1.2 粒子滤波及其缺陷在实际的应用中,贝叶斯滤波式 (1) 中的积分是很难实现的,而且在许多情况下,状态量的解析解是不存在的,因此只能用算法去逼近真实的后验概率密度,由此产生了粒子滤波算法。它的原理是用一组带有权值的随机样本来估算状态量的后验概率密度。当随机样本足够大的时候,样本均值就可等于后验概率密度。这些样本即为“粒子”。
根据蒙特卡洛仿真理论,假设从目标状态的后验概率分布p (xk|z1:k) 中抽取N个独立同分布的粒子集{x0:ki}(i=1, 2, …, N),则k时刻的后验概率分布可离散的加权为
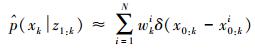 (3)
(3) 式中,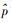
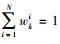
但在实际应用中后验概率分布p (xk|z1:k) 是很难直接采样的。SIS算法则能很好地解决该问题。该算法的主要思想是对一个已知的容易采样的密度函数q (xk|z1:k) 做采样和加权近似,并采用递推的形式计算粒子的重要性权值。则重要性权值可以表示为
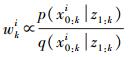 (4)
(4) 在给定的马尔科夫模型里面,对后验概率密度函数进行分解,再代回式 (4),递推可得重要性权值的更新公式为
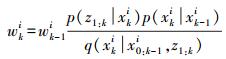 (5)
(5) 由此可得到粒子的权值,从而得到后验概率密度。
常规粒子滤波采用SIS算法虽然减少了计算量,大大方便了后验概率的计算。但是由于在计算中常采用先验的状态转移概率密度作为采样的密度函数。样本没有考虑系统状态的最新观测值,使滤波结果过渡依赖于模型。而且递推运算会不断加大重要性权重的方差,使得参与计算的大部分粒子权重很小,影响滤波结果的精度,出现粒子退化现象。
为了缓解SIS中的粒子退化问题,Gordon等提出了SIR算法。该算法在SIS的基础上增加了重采样步骤。重采样方法是按照粒子的权值大小复制粒子。这样会导致权值大的粒子被复制多次,权值小的粒子基本不会被复制。粒子滤波的结果只依赖于几个粒子,而失去了粒子的多样性,出现粒子匮乏现象。
为了解决上述两个问题,本文提出了一种改进的粒子滤波算法——基于高斯粒子群优化的无迹粒子滤波。该算法不仅优化重要性函数的选择,还能很好地改进粒子匮乏现象。
2 高斯粒子群优化的无迹粒子滤波 2.1 无迹粒子滤波粒子滤波中,为求解方便,一般选取先验概率密度函数为重要性函数,它是由系统的状态模型推导而来,未计入k时刻的观测值,会使滤波结果严重依赖于模型,同时粒子会偏移。若模型参数不准确或测量的噪声发生突变,滤波的结果会与真实分布有较大差异。UPF改进了滤波重要密度函数的选择,使用UKF产生粒子滤波的重要性分布函数,选取无迹变换 (unscented transformation,UT) 变换后的Sigma点作为样本,故由UKF产生的重要性分布与真实状态的重叠部分更多,估计精度更高,可得到优于普通粒子滤波的建议分布。
由于粒子滤波中预测阶段的状态量在时间序列上是满足一阶马尔科夫过程的,因此建议公式可写为
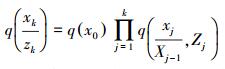 (6)
(6) 式中,xk和zk分别表示时刻k的所有状态和观测值的序列集合。
无迹粒子滤波与普通粒子滤波相比,充分利用了最新的观测值,使样本更加接近于系统的真实状态,对于非高斯的模型准确度更高。同时,UT变换产生的密度函数更接近真实的后验概率密度。
2.2 高斯粒子群算法PSO算法的具体实现过程为:随机生成一个初始粒子种群,种群中的每一个粒子都具有位置X=(xi1, xi2, …, xij) 和速度vi=(vi1, vi2, …, vij),由目标函数定义一个适应度函数。粒子在空间内不断运动,用两个极值来迭代寻找最优解。在每一次迭代中,粒子根据下式来更新自己的速度和位置
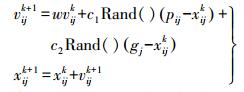 (7)
(7) 式中,pij是第i个粒子从初始到当前运动中的最优解,即为个体极值;gj是粒子种群从初始到当前运动的最优解,即为全局极值;Rand () 为在 (0, 1) 内的随机数;w为惯性系数;c1和c2为移动权重,决定了粒子向个体极值和全局极值移动的权重。
粒子群优化算法因为不是简单地复制粒子,而是让粒子在全局移动,很好地解决了粒子滤波中的粒子匮乏问题。但是,由于惯性系数w、移动权重c1和c2很难确定,粒子的运动速度也不好控制,因此krohling等[4]在2004年提出了一种改进算法,即高斯粒子群优化算法 (Gaussian particle swarm optimization,GPSO)。该算法不需要确定其他系数,只需要给出粒子数目就可以计算,具体方法如下
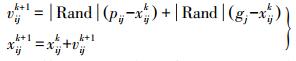 (8)
(8) GPSO算法通过不断迭代更新粒子的位置,使每个粒子向最优解靠近,而且大大简化了算法的更新效率,提高了粒子群的性能,能更方便地获得目标真实位置的最优估计。
2.3 基于高斯粒子群优化的无迹粒子滤波由上文可知,利用GPSO-UPF,性能优于普通的粒子滤波,改进之处表现在如下几个方面:
(1) 无迹粒子滤波可以使粒子的选择靠近观测值区间,贴近实际的状态,提高了滤波的精度。
(2) 普通粒子滤波使用的是次优重要性函数,因此重要性采样的结果是次优的粒子。引入高斯粒子群算法,可以很好地优化重采样过程,改善采样的精度。
(3) 使用高斯粒子群优化无迹粒子滤波,既能弥补UPF算法粒子多样性的不足,又能提高计算效率。同时解决了粒子退化和粒子匮乏的问题。
GPSO-UPF算法的具体实现步骤:
2.3.1 粒子初始化k=0的初始时刻,在系统模型预测出的先验概率分布p(x0) 中采集n个粒子组成粒子群并定义为{x0i}(i=1, 2, …, n)。其中每个粒子的权重均为1/n。计算出粒子群的初始均值与方差。
2.3.2 重要性采样(1) 使用无迹卡尔曼滤波算法更新粒子群中各粒子的状态,再用无迹粒子滤波算法更新粒子得到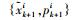
(2) 计算UPF算法得到的粒子群集合{xki}(i=1, 2,…,N) 的均值和方差。
(3) 从重要性密度函数中抽样新粒子样本集。
2.3.3 权值归一化(1) 更新系统状态与测量。
(2) 通过预测来获得新状态对应的观测量,计算粒子权值并进行归一化。归一化权值为
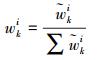 (9)
(9) (1) 设定最大迭代次数n。
(2) 确定粒子的权值函数为适应度函数。
(3) 初始化粒子群中各粒子的位置和速度,计算各粒子的适应度。
(4) 确定全局极值gj和个体极值pij。
(5) 利用速度更新公式和位置更新公式 (8) 对状态为存在的粒子进行更新获得更新后的粒子群。
(6) 寻找当前时刻权值最大的粒子更新适应度函数值、个体极值和全局极值。
(7) 运行到最大迭代次数后,停止搜索,输出最后的优化结果。
2.3.5 更新计算得到k时刻系统的后验概率估计值。
2.3.6 递推令k=k+1,返回2.3.2节,递推下一时刻目标状态的后验概率。
3 仿真试验本文利用一维单变量非线性增长模型 (univariate nonstationary growth model,UNGM) 验证高斯粒子群优化无迹粒子滤波算法的性能。该模型如下:
系统模型
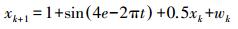 (10)
(10) 观测模型
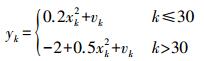 (11)
(11) 式中,wk是系统噪声,服从gamma分布且wk~Γ(3, 2);vk是测量噪声,服从正态分布且vk~N (0, 10-5)。其他参数设定为:先验概率p(x0)=N(0, 2),初始状态x1=0.1。选取PF、UPF、GPSO-UPF 3种算法进行试验。各算法采用相同的时间步长T=50 s,仿真次数R=50。同时为了研究粒子个数对算法的影响,分别选取50和500的粒子数进行仿真试验。
试验中不同算法的性能评定使用RMSE。公式为
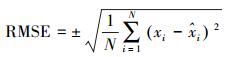 (12)
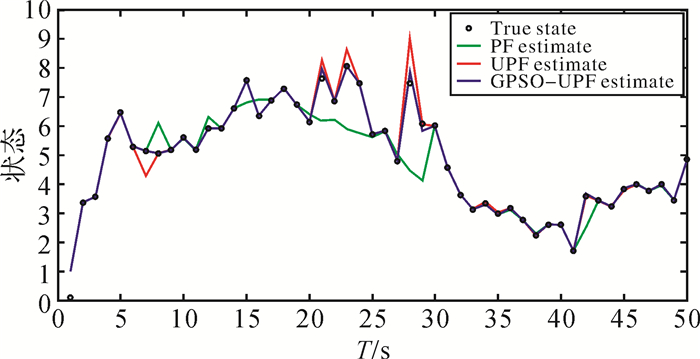
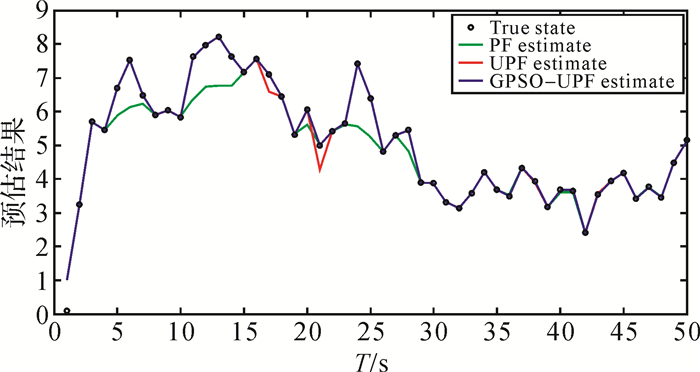
(12) N=50时单次试验的估计仿真如图 1所示。N=500时单次试验的估计仿真如图 2所示。图中展示了一次仿真中每个时刻的真实值及粒子滤波、无迹粒子滤波、高斯粒子群优化的无迹粒子滤波的估计值。表 1给出了不同粒子数时各算法均方根误差的均值、方差及运行时间。
|
| 图 1 N=50条件下不同滤波器预估结果 |
|
| 图 2 N=500条件下不同滤波器预估结果 |
| 算法 | 粒子数 | REMS均值 | REMS方差 | 运行时间/s |
| PF | 50 | 0.8219 | 0.0476 | 0.1887 |
| PF | 500 | 0.3786 | 0.0659 | 1.5422 |
| UPF | 50 | 0.2737 | 0.0214 | 1.1191 |
| UPF | 500 | 0.1913 | 0.0012 | 10.9503 |
| GPSO-UPF | 50 | 0.1983 | 0.0138 | 1.4956 |
| GPSO-UPF | 500 | 0.1592 | 0.0011 | 12.0277 |
由图 1、图 2可以看出,当粒子数较少 (N=50) 时,PF算法和真实值差异较大,UPF算法也不稳定,而GPSO-UPF的性能则优于其他算法,已经与真实状态非常接近。当粒子数较多 (N=500) 时,PF算法依然有偏差,UPF算法虽然有提升,但仍然存在误差,GPSO-UPF算法最为贴近真实值。从表 1可以看到,粒子数的选取将直接影响滤波的估计精度。粒子数越多,同一滤波的精度越高。但同时粒子数的增多会耗费更多的运行时间。其中,PF受粒子数影响最为明显,精度也最低。UPF随着粒子增多,精度也提高。GPSO-UPF在相同粒子数的条件下精度最高,稳定性也最好。
试验表明,GPSO-UPF算法因为加入了高斯粒子群优化,效果明显好于UPF算法。该算法明显提升了滤波的性能,精度更高,得到的结果也更接近真实状态,稳定性更好。虽然该算法计算所需的时间略多于UPF算法,但是,通过不同粒子数的对比可看到,PF与UPF算法依赖于粒子数,只有在粒子数达到一定数目的时候,算法的精度才能明显提高。而GPSO-UPF算法不需要较多的粒子也能得到比较好的结果,节约了运行时间,大大提高了算法的效率。因此,该算法优于PF及UPF。
4 结语基于粒子滤波存在的次优估计与粒子匮乏问题,本文提出了一种新的GPSO-UPF算法。该算法使用无迹粒子滤波解决估计问题,充分利用最新的观测值,并用高斯粒子群算法优化重采样,提高了粒子多样性。不仅对于滤波的次优估计有明显的改善,还解决了粒子匮乏的缺陷。仿真试验结果表明,新算法具有较高的精度和稳定性,其性能优于传统的粒子滤波与无迹粒子滤波算法,且效率更高,只需要较少的粒子就能得到精确的结果。
| [1] | MERWE R V D, DOUCET A, FREITAS N D, et al. The Unscented Particle Filter[J]. Advances in Neural Information Processing Systems, 2001, 13: 584–590. |
| [2] | KENNEDY J, EBERHART RC. Particle Swarm Optimization[J]. IEEE International Conference on Neural Networks, 1995, 4(8): 1942–1948. |
| [3] | KOTECHA J H, DJURIĆ P M. Gaussian Particle Filtering[J]. IEEE Transactions on Signal Processing, 2003, 51(10): 2592–2601. DOI:10.1109/TSP.2003.816758 |
| [4] | ARULAMPALAM M S, MASKELL S, GORDON N, et al. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174–188. DOI:10.1109/78.978374 |
| [5] | KROHLING R A. Gaussian Swarm: A Novel Particle Swarm Optimization Algorithm[C]//IEEE Conference on Cybernetics and Intelligent Systems.[S.l.]:IEEE, 2004. |
| [6] | WANG D, ZENG P, LI L, et al. A Novel Particle Swarm Optimization Algorithm[C]//IEEE International Conference on Software Engineering and Service Sciences. [S.l.]:IEEE, 2010:408-411. |
| [7] | THRUN S. Particle Filters in Robotics[J]. Eighteenth Conference on Uncertainty in Artificial Intelligence, 2002, 19(2): 511–518. |
| [8] | DOUCET A, GORDON N, KRISHNAMURTHY V. Particle Filters for State Estimation of Jump Markov Linear Systems[J]. IEEE Transactions on Signal Processing, 2001, 49(3): 613–624. DOI:10.1109/78.905890 |
| [9] | DOUCET A. On Sequential Simulation-based Methods for Bayesian Filtering[D]. Cambridge:University of Cambridge, 1998. |
| [10] | BAY K S, LEE S J, FLATHMAN D P, et al. Sequential Imputations and Bayesian Missing Data Problems[J]. Journal of the American Statistical Association, 1994, 89(425): 278–288. DOI:10.1080/01621459.1994.10476469 |
| [11] | 方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法[J]. 控制与决策, 2007, 22 (3) : 273–277. |
| [12] | 陈国良, 张言哲, 汪云甲, 等. WiFi-PDR室内组合定位的无迹卡尔曼滤波算法[J]. 测绘学报, 2015, 44 (12) : 1314–1321. |
| [13] | 薛长虎, 聂桂根, 汪晶. 扩展卡尔曼滤波与粒子滤波性能对比[J]. 测绘通报, 2016 (4) : 10–14. |
| [14] | 邹韬, 赵长胜, 丁圳祥. 有色观测噪声下的无迹卡尔曼滤波算法[J]. 测绘通报, 2015 (6) : 24–27. |
| [15] | 王法胜, 鲁明羽, 赵清杰, 等. 粒子滤波算法[J]. 计算机学报, 2014, 37 (8) : 1679–1694. |
| [16] | 任航. 基于拟蒙特卡洛滤波的改进式粒子滤波目标跟踪算法[J]. 电子测量与仪器学报, 2015 (2) : 289–295. |


