Download PDF  
文章快速检索  
  高级检索
引用本文
李兴桥， 章传银， 王伟，等。 固体潮对三峡地区地壳垂直形变和重力变化的影响分析[J]. 测绘通报，2017(3)：9-12. DOI: 10.13474/j.cnki.11-2246.2017.0073.
LI Xingqiao, ZHANG Chuanyin, WANG Wei, et al. Influence Analysis of Solid Tide on Vertical Crustal Deformation and Gravity Changes in the Three Gorges Area[J]. Bulletin of Surveying and Mapping, 2017(3): 9-12. DOI: 10.13474/j.cnki.11-2246.2017.0073.
固体潮对三峡地区地壳垂直形变和重力变化的影响分析
李兴桥1,2, 章传银2, 王伟2, 杨阳2,3, 尹财1,2, 柯宝贵2     
1. 山东科技大学测绘科学与工程学院, 山东 青岛 266590;
2. 中国测绘科学研究院, 北京 100830;
3. 兰州交通大学, 甘肃 兰州 730070
收稿日期：2016-10-16; 修回日期：2017-01-17
基金项目：重点研发计划（2016YFB0501702）
作者简介：李兴桥 (1988-), 男, 硕士生, 研究方向为海洋测高。E-mail:812502452@qq.com
摘要：利用IERS协议上的方法和DE405星历文件，基于三峡地区CORS站和重力台站位置，计算了从2011年到2015年6月固体潮每2 h对三峡地区地壳垂直形变和重力变化的影响，并计算了2012年12月14日大潮期间固体潮影响分布。研究发现，三峡地区固体潮有很强的周期性，存在半月和半年的长周期、一天和半天的短周期。三峡地区农历每月月中和月底前后有2次大潮，月中和月底的大潮潮差相差约1/4；每年冬季（月球赤纬28°36'，约11、12、1月）和夏季（约5、6、7月，太阳高度角接近最大）大潮潮差大，春季和秋季大潮潮差小。大地高最大潮高0.346 m，最低潮高-0.190 m（参考历元2000.0）；固体潮对重力与对垂直形变影响异相，最大值110 μGal，最小值-200 μGal。区域固体潮呈明显的条带分布，固体潮对垂直形变与重力变化影响的增减方向相反。本文的研究成果可用于CORS站、重力台站的固体潮影响分析，为局部固体潮相关研究提供参考。
关键词：三峡地区     固体潮     垂直形变     重力固体潮    
Influence Analysis of Solid Tide on Vertical Crustal Deformation and Gravity Changes in the Three Gorges Area
LI Xingqiao1,2, ZHANG Chuanyin2, WANG Wei2, YANG Yang2,3, YIN Cai1,2, KE Baogui2     
1. School of Geomatics, Shandong University of Science and Technology, Shandong, Qingdao 266590, China;
2. Chinese Academy of Surveying and Mapping, Beijing 100830;
3. Lanzhou Jiaotong University, Lanzhou 730070, China
Abstract: In this paper, using the method of IERS protocol and DE405 ephemeris file, based on the CORS station and gravity station located in the Three Gorges area, the vertical crustal deformation and gravity changes in Three Gorges area from 2011 to June 2015 tide every 2 hours are calculated, and the spring tide tide influence distribution on December 14, 2012 is calculated. The results indicated that the solid tide in Three Gorges area has very strong periodicity, the long period of half month and half year, the short period of one day and half day.There are 2 times spring tide in Three Gorges area before and after the end of the per lunar month, the middle of a month and month at the end of the spring tide range is about 1/4; the annual winter (lunar declination 28 or 36, about November, December and January) and summer (about May, June and July, the solar altitude angle is close to the maximum tide) large tidal range, the spring and autumn small tidal range. High maximum tidal geodetic height 0.346 m and neap high-0.190 m (reference epoch 2000.0); solid tide on gravity and the vertical deformation of heterogeneous, a maximum of 110 μGal, minimum-200 μGal. Regional solid tide is obvious strip distribution, solid tide of vertical deformation and gravity changes influence the increase or decrease in the opposite direction. The research results of this paper can be for CORS, gravity stations of solid tide effect analysis, which provide a reference for related studies of the local solid tide.
Key words: Three Gorges area     solid tide     vertical deformation     Gravity solid tide    

地球是一个十分复杂的近似分层椭球体，内部各层面上的构成物相异，有弹性的、非弹性的、塑性的，甚至是液态的。地球上任何一点除受到地球本身吸引力和地球自转导致的惯性离心力的合力 (重力) 作用外，还受日月和其他天体的引潮力。在引潮力作用下，地球固体部分也会像海潮一样时刻发生周期性变化，通常将这种现象称为地球固体潮。固体潮的存在将伴随各种各样的地球物理场变化 (如重力、倾斜、应变和地表位移等)[1]。

三峡库区自2003年建库以来经研究发现地震、泥石流、滑坡等地质灾害明显增加，因此成为人们关注的热点地区。三峡工程蓄水完成后，对地壳的稳定性产生了巨大的影响，为监测构造稳定性在三峡地区建立了CORS变形监测网络和地面重力监测网络。随着测量技术的发展，对传统测量误差处理已经可以达到高精度监测的要求。为了获得更加准确的监测结果，固体潮影响必须从观测值中剥离[2-3]。由于三峡地区缺少实测的固体潮模型，在观测值中剔除固体影响时仍需计算固体潮理论模型。同时，大地测量基准的建立、维持过程中也必须考虑固体潮对大地测量基准随时间的影响。

在空间大地测量数据处理中，固体潮影响理论计算逐渐趋于IERS标准。因此，本文基于该地区的CORS站和重力台站的位置，利用IERS2010协议上的方法和1988年发布的DE405星历文件，计算了固体潮对该地区垂直形变和重力变化的影响，并分析了固体潮的时间、空间特征[4-5]。

1 固体潮影响的计算方法 1.1 固体潮对垂直形变影响的计算

引潮位对测站位移的间接影响通过位移勒夫数 (Love数hnm和Shida数lnm) 来表征。对于实际地球，位移勒夫数既依赖于测站纬度，又依赖于潮汐频率。为顾及纬度的相关性，IERS协议采用Mathews理论的位移勒夫数多重表达方式，给出了各分潮引起的地面测站位移的向量表达式[6-10]。对测站的垂直形变改正到无潮汐系统下，改正量等于时间域的计算与频率域的改正之和。

1.1.1 时间域的计算 1.1.1.1 计算二阶潮引起的位移

利用二阶引潮力位的时间域的表达式计算对测站的间接影响[11]，用一致的标称值h2和l2计算所有分潮潮，以便使计算量最小。二阶标称值计算的二阶引潮力对测站潮汐位移的影响是主要影响，使用常数Love数和Shida数的标称值h2和l2计算方案如下

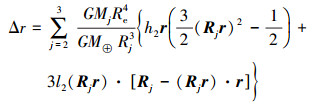(1)

式中，GM⊕为地心引力常数；GMj为月心 (j=2) 和日心 (j=3) 引力常数；Re为地球赤道半径；Rj和Rj分别为地心至月球或太阳的单位矢量和大小；r和r分别为地心至测站的单位矢量和大小。

1.1.1.2 计算三阶潮引起的位移

用三阶Love数和Shida数的标称值h3和l3计算的测站位移矢量为

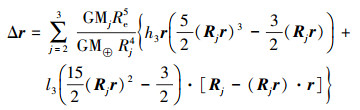(2)

此式只许应用于月球 (j=2)，由此算得到的径向位移可达1.7 mm。

1.1.1.3 计算由h2m(0)引起的虚部贡献量

计算地幔滞弹性时，在二阶Love数和Shida数中要引入虚部hI和lI。周日潮产生的径向 (hI=-0.002 5) 为

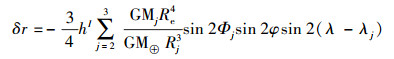(3)

半日潮产生的贡献为 (hI=-0.002 2)

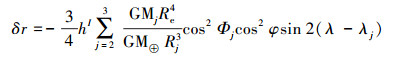(4)

式 (3)—式 (4) 中，Φj为太阳或月球的地心纬度；λj为太阳或月球的地心经度；φ为地面点的纬度；λ为地面点的经度。

1.1.2 频率域的计算

Love数和Shida数的频率相关改正如下：

计算周日潮引起的垂直变化改正

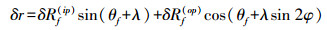(5)

计算长周期项引起的垂直变化改正

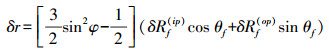(6)
1.2 重力固体潮的计算

对重力同样改正到无潮汐系统下，具体计算包括以下4部分。改正值等于4部分之和[12-14]。

(1) 采用与频率无关的Love数knm，计算在时间域引潮位在正常位上的变化

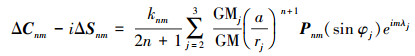(7)

(2) 采用频率相关的位Love数k2m(+)，由二阶引潮位计算四阶位系数变化

(8)

(3) 所有长周期项对ΔC20频率改正的总影响[15]为

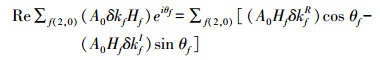(9)

(4) 周日潮对ΔC21-iΔS21的影响的改正以及半日潮对ΔC22-iΔS22的影响的改正为

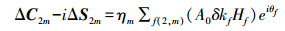(10)
2 三峡地区固体潮计算

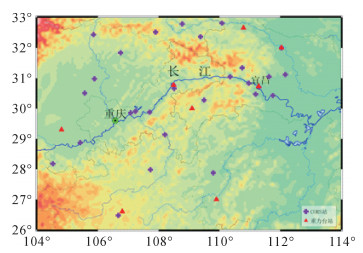
研究区域的CORS站与重力台站分布如图 1所示。

图 1 研究区域及站点位置
图选项

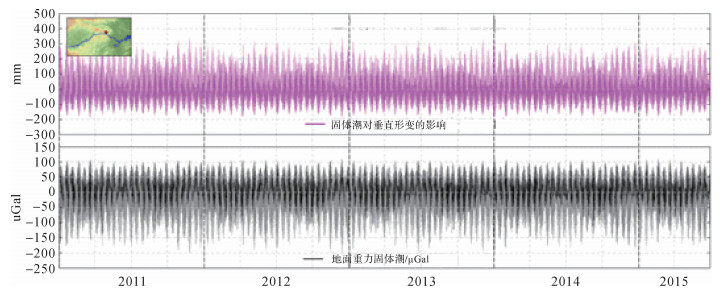
利用IERS协议上的方法和DE405星历文件，基于三峡地区CORS站和重力台站位置，计算了从2011年到2015年6月固体潮每2 h对三峡地区地壳垂直形变和重力变化的影响。固体潮对宜昌站的影响如图 2所示。为发现其短周期规律，图 3展示了2013年5、6、7三个月的变化。并对重力固体潮时间序列作了功率谱分析，如图 4所示。

图 2 固体潮对宜昌站的影响 (2011—2015-06)
图选项
图 3 固体潮对宜昌站的影响 (2013-05—2013-07)
图选项
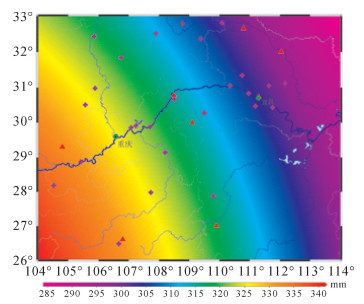
图 4 三峡地区大潮期间固体潮对垂直形变的影响
图选项

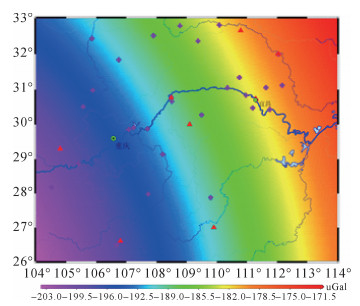
从图 2、图 3中可以看出三峡地区固体潮有很强的周期性。存在半月和半年的长周期、一天和半天的短周期。三峡地区农历每月月中和月底前后有2次大潮，月中和月底的大潮潮差相差约1/4；每年冬季 (月球赤纬28°36′，约11、12、1月) 和夏季 (约5、6、7月，太阳高度角接近最大) 大潮潮差大，春季和秋季大潮潮差小。大地高最大潮高0.346 m，最低潮高-0.190 m (参考历元2000.0)；固体潮对重力与对垂直形变影响异相，最大值为110 μGal，最小值为-200 μGal。为了研究固体潮影响的区域特点，计算了2012年12月14日大潮期间固体潮影响分布。如图 4、图 5所示。区域固体潮呈明显的条带分布，固体潮对垂直形变与重力变化影响的增减方向相反。

图 5 三峡地区大潮期间重力固体潮分布
图选项
3 结语

本文基于三峡地区CORS站和重力台站位置，计算了三峡地区地壳垂直形变和重力变化的影响，并计算了大潮期间固体潮影响分布。固体潮对垂直形变的影响和对重力的影响存在明显的周期性。存在半月和半年、一年的长周期，一天和半天的短周期。区域固体潮呈明显的条带分布，固体潮对垂直形变与重力变化影响的增减方向相反。本文的研究成果可用于三峡地区的CORS站、重力台站的测量数据处理中移去固体潮影响，为局部固体潮相关研究提供参考。

参考文献
[1] 陈晓东, 孙和平, 胡国庆, 等. 三峡水库首区重力固体潮观测资料分析[J]. 地震学报, 2007, 29 (5) : 492–499.
[2] 殷海涛, 李杰, 马丕峰, 等. 固体潮模型对GPS时间序列的影响研究[J]. 大地测量与地球动力学, 2009, 29 (2) : 48–52.
[3] 何婵军, 杜志彪. 三峡库区垂直形变有限元模型分析[J]. 测绘科学技术学报, 2013, 30 (5) : 456–460.
[4] 张捍卫, 郑勇, 赵方权. 固体潮对测站位移影响的理论研究[J]. 大地测量与地球动力学, 2003, 23 (3) : 98–103.
[5] 王文利, 陈士银, 董鸿闻. 现行水准测量日月引力改正数学模型的分析与使用[J]. 测绘通报, 2000 (12) : 8–9.
[6] 王伟, 章传银, 杨强, 等. 固体潮对测站位移的影响特征分析[J]. 测绘通报, 2016 (3) : 7–9.
[7] 党亚民, 张传银, 陈俊勇, 等. 现代大地测量基准[M]. 北京: 测绘出版社, 2015.
[8] GOODKIND J M. Test of Theoretical Solid Earth and Ocean Gravity Tides[J]. Geophysical Journal International, 2007, 125(1): 106–114.
[9] 董春来, 路长城, 郭淑艳, 等. 海潮对GNSS高精度测量影响的研究[J]. 测绘通报, 2011 (2) : 4–5.
[10] GÉRARD P, BRIAN L. IERS Conventions (2010)[M]. Frankfurt am Main: Verlag des Bundesamts fur Kartographie and Geodäsie, 2010.
[11] CARTWRIGHT D E, TAYLER R J. New Computations of the Tide-generating Potential[J]. Geophysical Journal of International, 1971, 23(1): 45–73.
[12] 张捍卫, 许厚泽, 王爱生. 固体潮对地球重力场时变特征影响的潮波公式[J]. 测绘学报, 2004, 33 (4) : 299–302.
[13] 张捍卫, 郑勇, 赵方权. 固体潮对测站位移影响的理论研究[J]. 大地测量与地球动力学, 2003, 23 (3) : 98–103.
[14] 张捍卫, 柴洪洲, 王占统, 等. 地球自转和固体潮对地球重力场时变特征的影响[J]. 大地测量与地球动力学, 2002, 22 (1) : 76–80.
[15] MATHEWS P M, BUFFETT B A, SHAPIRO I I. Love Numbers for Diurnal Tides:Relation to Wobble Admittances and Resonance Expansions[J]. Journal of Geophysical Research Atmospheres, 1995, 100(B6): 9935–9948. DOI:10.1029/95JB00670
http://dx.doi.org/10.13474/j.cnki.11-2246.2017.0073
国家测绘地理信息局主管、中国地图出版社（测绘出版社）主办。
0

文章信息

李兴桥， 章传银， 王伟， 杨阳， 尹财， 柯宝贵
LI Xingqiao, ZHANG Chuanyin, WANG Wei, YANG Yang, YIN Cai, KE Baogui
固体潮对三峡地区地壳垂直形变和重力变化的影响分析
Influence Analysis of Solid Tide on Vertical Crustal Deformation and Gravity Changes in the Three Gorges Area
测绘通报，2017(3)：9-12.
Bulletin of Surveying and Mapping, 2017(3): 9-12.
http://dx.doi.org/10.13474/j.cnki.11-2246.2017.0073

文章历史

收稿日期：2016-10-16
修回日期：2017-01-17

相关文章

工作空间