2. 中国测绘科学研究院, 北京 100830;
3. 建设综合勘察研究设计院有限公司, 北京 100007
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. China Institute of Geo-technical Investigation and Surveying Co. Ltd., Beijing 100007, China
在GNSS载波相位观测过程中,为构建高质量周跳检验量,对多类卫星系统的数据质量分析研究越来越重要。尤其是我国北斗卫星导航定位系统的快速发展,使得对它的研究进一步深入,本文从3个方面分析了各种轨道的BDS卫星数据质量[1]。
1 多路径效应多路径效应是指接收机除直接收到卫星发射的信号外,还同时接收测站附近的物体表面一次或多次反射的信号,这种不同路径的信号与直接信号叠加,产生的时延效应称为多路径误差。多路径误差主要受观测环境的影响,伪距的多路径误差最大可达0.5个码元宽度;载波相位的波长短,约为伪距的1/1000,载波相位观测值的多路径误差一般不超过1/4波长,其测量噪声和多径效应要比伪距小得多,因此主要考虑伪距多路径的影响[2]。
相比于伪码,载波相位的多路径影响可以忽略,因此,通过载波相位观测值和伪距观测值之差来求得伪距的多路径误差,观测方程可表示为
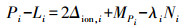 (1)
(1) 由电离层折射的弥散特性可知,Δion, 1和Δion, 2有以下特性
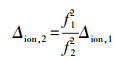 (2)
(2) 假设两个频率的载波在对流层中的传播路径相同,则在两个载波上的电离层延迟可表示为
 (3)
(3) 将式 (3) 代入式 (1) 可得
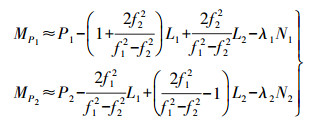 (4)
(4) 由于相位模糊度的存在,得到的多路径与实际值存在系统性偏差,要求出多路径的真实量,必须准确地求出整周模糊度,而模糊度的求解复杂,因此采用移动平均的方法计算伪距的多路径值。在不发生周跳的情况下,两载波的整周未知数为常数,选择一个序列,计算出移动窗口内多路径的平均值,再用伪距瞬时多路径减去这一平均值,就得到多路径效应的幅值,获得正确的多路径值。
利用KARR、PERT、TOW2测站2016年1月10—12日3 d的观测数据分析GPS与BDS数据多路径效应的影响,数据采样间隔为30 s。
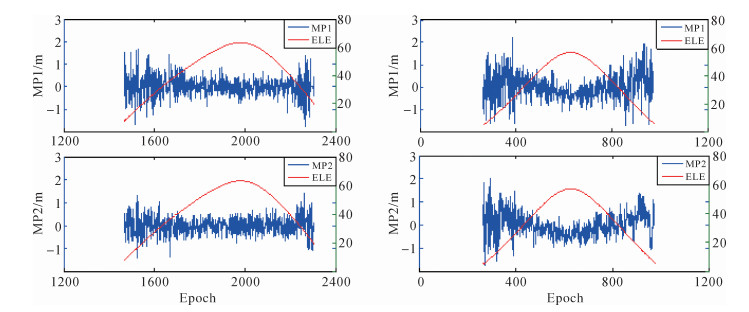
1.1 同一测站GPS与BDS观测数据多路径效应分析选取PERT站2016年1月10日的观测数据进行分析,图 1表示PERT站GPS卫星与BDS的MEO卫星多路径效应随高度角的变化;图 2表示PERT站BDS的GEO与IGSO卫星多路径效应随高度角的变化。
|
| 图 1 PERT站G03与C14卫星多路径效应随高度角变化 |

|
| 图 2 PERT站C03与C06卫星多路径效应随高度角变化 |
由图可以看出,所有卫星在高度角较低时,多路径效应值相对较大,当高度角升高时,多路径效应明显下降;BDS卫星由于其星座的特殊性,多路径效应表现出与GPS不同的特点,其MEO卫星高度角变化规律与GPS卫星一致;GEO卫星由于其轨道的特殊性,高度角变化较小,多路径变化较为稳定。
1.2 不同测站BDS各轨道卫星观测数据多路径效应分析BDS系统星座是由GEO、IGSO、MEO 3种不同轨道卫星组成的,选取KARR、PERT、TOW2测站2016年1月10—12日3 d的观测数据,分别在B1、B2频点对3种轨道卫星多路径效应进行分析。
表 1表示BDS各轨道卫星B1频点多路径效应, 表 2表示BDS各轨道卫星B2频点多路径效应,图 3表示BDS各轨道卫星两频点多路径效应站平均值。由图 3和表 1、表 2可看出,不论在B1频点还是在B2频点,多路径效应均呈现出GEO < IGSO < MEO的现象,且BDS各轨道卫星在B1上的多路径效应均大于在B2上的多路径效应。
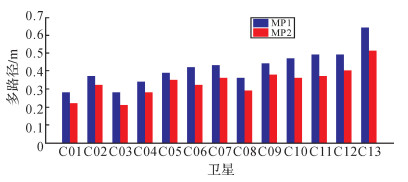
|
| 图 3 BDS各轨道卫星多路径效应站平均值 |
| m | ||||
| 卫星 | 测站 | |||
| KARR | PERT | TOW2 | 站平均 | |
| GEO-1 | 0.28 | 0.36 | 0.20 | 0.28 |
| GEO-2 | 0.37 | 0.42 | 0.32 | 0.37 |
| GEO-3 | 0.23 | 0.37 | 0.25 | 0.28 |
| GEO-4 | 0.33 | 0.47 | 0.22 | 0.34 |
| GEO-5 | 0.46 | 0.32 | — | 0.39 |
| IGSO-1 | 0.48 | 0.45 | 0.34 | 0.42 |
| IGSO-2 | 0.46 | 0.46 | 0.38 | 0.43 |
| IGSO-3 | 0.32 | 0.39 | 0.37 | 0.36 |
| IGSO-4 | 0.52 | 0.42 | 0.38 | 0.44 |
| IGSO-5 | 0.43 | 0.51 | 0.45 | 0.47 |
| MEO-1 | 0.51 | 0.47 | 0.48 | 0.49 |
| MEO-2 | 0.53 | 0.61 | 0.34 | 0.49 |
| MEO-4 | 0.68 | 0.56 | 0.69 | 0.64 |
| m | ||||
| 卫星 | 测站 | |||
| KARR | PERT | TOW2 | 站平均 | |
| GEO-1 | 0.24 | 0.29 | 0.13 | 0.22 |
| GEO-2 | 0.26 | 0.36 | 0.34 | 0.32 |
| GEO-3 | 0.22 | 0.26 | 0.15 | 0.21 |
| GEO-4 | 0.39 | 0.32 | 0.12 | 0.28 |
| GEO-5 | 0.34 | 0.36 | — | 0.35 |
| IGSO-1 | 0.34 | 0.37 | 0.24 | 0.32 |
| IGSO-2 | 0.39 | 0.44 | 0.26 | 0.36 |
| IGSO-3 | 0.27 | 0.29 | 0.29 | 0.29 |
| IGSO-4 | 0.46 | 0.37 | 0.31 | 0.38 |
| IGSO-5 | 0.33 | 0.43 | 0.32 | 0.36 |
| MEO-1 | 0.35 | 0.38 | 0.38 | 0.37 |
| MEO-2 | 0.42 | 0.51 | 0.26 | 0.40 |
| MEO-4 | 0.50 | 0.55 | 0.48 | 0.51 |
信噪比是指载波信号强度和噪声强度的比值。它主要受天线的增益参数、接收机相关器状态及多路径误差的影响,是反映载波相位观测质量的指标之一[3]。信噪比可以从观测文件中直接获得,其数值越大,表示信号强度越强。
选取KARR、PERT、TOW2测站2016年1月10—15日6 d的观测数据,分析GNSS不同系统卫星数据的信噪比及北斗各轨道卫星数据信噪比随时间的变化情况。
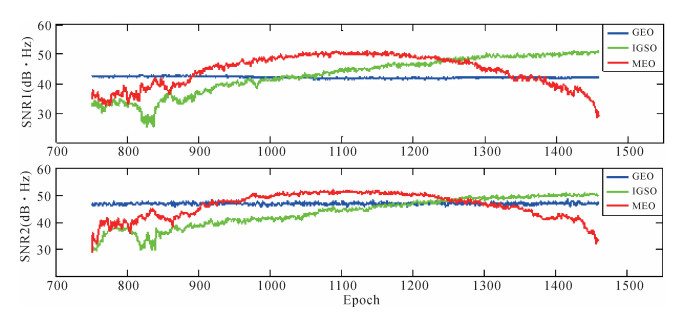
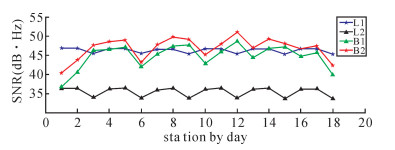
信噪比与信号强度息息相关,是反映GNSS载波信号质量的重要指标之一。图 4表示TOW2站BDS 3个轨道上卫星数据信噪比随时间的变化情况,图 5表示GPS与BDS卫星两频点数据的信噪比情况。可以看出,BDS系统GEO卫星由于轨道的特殊性,其数据信噪比变化较平稳,MEO卫星数据信噪比变化较大;GPS卫星在L1频点的信噪比明显大于L2频点的信噪比,而BDS卫星在B2频点上的信噪比略大于B1的信噪比,且B1、B2数据的信噪比都高于L2的信噪比。
|
| 图 4 TOW2站BDS各轨道卫星数据信噪比 |
|
| 图 5 GPS与BDS卫星两频点数据信噪比 |
GNSS观测数据除了包含周跳和粗差,还包含接收机钟跳。理论上接收机总是将内部时钟与GNSS时间同步,由于石英钟的精度局限,此同步并不严格,为保持同步,需要周期地插入接收机的时钟跳跃,这个跳跃则为钟跳[4-6]。钟跳是干扰粗差和周跳探测的一个重要因素[7],钟跳与周跳十分类似,都会引起观测数据的跳变,但两者在原理和实质上是不同的,钟跳是接收机钟差的突然变化,可以引起所有卫星伪距或载波相位观测值的同时跳变[8]。钟跳能够导致现有的部分周跳探测方法失效,钟跳探测的正确与否直接关系着非差数据处理的精度和效率,因此有必要在周跳探测之前消除时钟跳跃对观测量的影响[9]。
不同的接收机有两种典型的钟跳:频繁跳跃和毫秒跳跃[10]。频繁跳跃是在每个历元对接收机时钟进行修正,改正量一般较小,一般情况下可以不考虑;毫秒跳跃是在接收机钟差达到一定数值时才进行修正。本文主要是针对毫秒跳跃的接收机进行钟跳探测。
本文采用双频相位观测值的O-C值进行探测,通过消电离层线性组合计算相位残差值
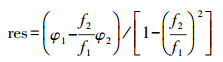 (5)
(5) 毫秒钟跳产生的相位周数可表示为
 (6)
(6) 如果满足条件
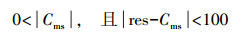 (7)
(7) 则存在毫秒钟跳,其大小为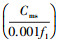
选取POL2测站2015年220 d的观测数据,以G05星与G15星为例,探测各卫星载波相位观测值的钟跳情况。
图 6为POL2站G05与G15星载波相位观测值钟跳探测结果。从图中可以看出,G05星的载波相位观测值在历元105处相位残差值res发生突变,此时发生钟跳,钟跳值为3 ms;G15星相位残差值res变化较小,不存在钟跳现象。
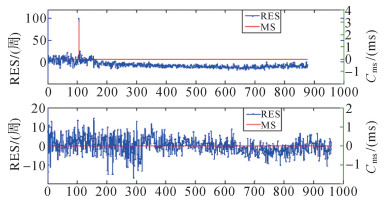
|
| 图 6 POL2站G05与G15星载波相位观测值钟跳探测结果 |
本文依据GNSS数据观测质量指标,采用MGEX观测站数据,详细分析了GPS与BDS卫星数据的多路径效应与信噪比。得出卫星在高度角较低时,多路径效应值相对较大,当高度角升高时,多路径效应明显下降;BDS系统的GEO卫星由于其轨道的特殊性,高度角变化较小,多路径变化较为稳定;不论在B1频点还是在B2频点,BDS卫星多路径效应均呈现出GEO < IGSO < MEO的现象,且BDS各轨道卫星在B1上的多路径效应均大于在B2上的多路径效应。BDS系统GEO卫星由于其轨道的特殊性,其数据信噪比变化较平稳,而MEO卫星数据信噪比变化相对较大;GPS卫星在L1频点的信噪比明显大于L2频点的信噪比,而BDS卫星在B2频点上的信噪比略大于B1的信噪比。
另外,多模GNSS接收机的内部石英钟不稳定,易发生钟跳。当钟跳发生时,从数据预处理的角度分析,应先进行钟跳的探测与标记,再进行周跳探测。
| [1] | 葛燕飞, 付亚梁, 杨银甲. TEQC软件在GPS数据预处理与质量分析中的应用[J]. 黑龙江科技信息, 2010, 12 (1) : 8–8. |
| [2] | UNAVCO. TEQC the Toolkit for GPS/GLONASS/Galileo/SBAS/BeiDou/QZSS Data[EB/OL].[2013-03-15]. http://facility.unavco.org/software/teqc/teqc.html. |
| [3] | 谭羽安, 袁本银, 鲍志雄. GPS/BD/GLONASS多星座质量检核研究与实现[C]//第四届中国卫星导航学术年会论文集. 武汉: 中国卫星导航学术年会, 2013. |
| [4] | 杨剑, 王泽民, 王贵文. GPS接收机钟跳的研究[J]. 大地测量与地球动力学, 2007, 27 (3) : 123–127. |
| [5] | 张成军, 贾学东. 接收机钟跳对GPS定位的影响及探测方法[J]. 测绘通报, 2009 (12) : 7–10. |
| [6] | GUO Fei, ZHANG Xiaohong. Realtime Clock Jump Detection and Repair Based on GNSS Observations[C]//CSNC. Guangzhou:[s.n.], 2012. |
| [7] | 吴丹. GNSS观测数据预处理及质量评估[D]. 西安: 长安大学, 2015. |
| [8] | 黄丁发, 熊永良, 袁林果. 全球定位系统 (GPS):理论与实践[M]. 成都: 西南交通大学出版社, 2006. |
| [9] | 张勤, 李家权. GPS测量原理及应用[M]. 北京: 科学出版社, 2012. |
| [10] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005: 116-119. |
| [11] | 崔阳, 吕志平, 陈正生, 等. 多核环境下的GNSS网平差数据并行处理研究[J]. 测绘学报, 2013, 42 (5) : 661–667. |


