2. 云南省测绘工程院, 云南 昆明 650033;
3. 陕西铁路工程职业技术学院, 陕西 渭南 714000
2. Surveying and Mapping Engineering Institute of Yunnan Province, Kunming 650033, China;
3. Shaanxi Railway Institute, Weinan 714000, China
地面LiDAR技术广泛应用于各种对象的精细三维重建,它所获得的点云数据具有海量性、散乱性、高空间分辨率等特性[1]。根据一定的属性或规则,将这些具有高空间分辨率的散乱点云数据划分为若干互不相交的子集的过程,称为点云数据分割[2],它广泛应用于基于特征的配准[3]、模型重建[4]、点云数据滤波与精简等[5]、语义分类[6],是激光点云数据处理中的一项基础性工作。目前,点云数据分割的方法主要分为基于边的方法和基于面的方法。基于边的方法是首先探测突变边界,根据闭合边界分割数据体;基于面的方法是根据对象的几何面片特性,将数据分为具有不同面片特征的数据集合。其中,基于面的方法能为人们提供点云数据的抽象表达,有利于后期的表达与分析,因此获得了广泛的认可[7]。
在基于面的方法中,随机采样一致性方法RANSAC(random sample consensus)是最为常用的方法,它具有内存消耗低,方法简单、通用、易扩展等特点,在实际中获得了广泛的应用[8]。如BOLLES利用RANSAC方法从距离影像中提取圆柱[9];CHAPERON利用RANSAC方法和高斯影像从点云数据中提取圆柱[10];王植利用RANSAC方法对机载激光点云数据进行平面分割以获取建筑物轮廓信息[11];皇甫中民利用RANSAC方法提取旋转特征面[12];Tarek M利用Seq-RANSAC方法从散乱点云数据中探测平面特征[13]。上述文献中都是从点云数据中识别一种几何特征,缺少多种几何面片探测机制。而现实人工对象多以不同规则几何形体有机构成,如何在这些人工对象所对应的点云数据中有效自动探测多种面片特征,在现实中具有重要意义。本文在传统RANSAC方法的基础上,提出基于局部采样优化和统计推断策略的多几何面片(本文以平面、柱面、球面为例)探测方法,最终实现点云数据分割。
1、 多几何特征探测方法 1.1. 基本原理在现实人工对象中,面片属于局部特征,高空间分辨率点云数据是对目标对象的冗余表达。传统RANSAC方法的全局采样策略扩大了探测多种几何面片特征所需的比对空间。当面片特征较多、体量较大时,势必造成探测效率的降低[14]。鉴于此,本文多种几何面片识别方法可表述为以下流程:
(1) 利用三维空间格网对当前点云数据进行空间划分,利用kd-Tree构建点的局部邻域,以满足点邻域搜索和属性计算。
(2) 在当前点集中随机抽取一待分类点,根据空间位置确定其所在的空间格网单元,在该格网单元内执行局部RANSAC方法以确定候选模型集。
(3) 确定各候选模型在邻域单元格网打分,利用数理统计中的方法推断各模型的全局打分,获得最优模型及其对应的一致集,并将一致集从当前数据集中分离出去。
(4) 循环以上过程,直至剩余点集为空或小于最小点集,从而完成分割。
1.2. 数据预处理在对点云数据分割之前,对点云数据作两项预处理:①为了提高分割过程中的邻域搜索效率,本文采用文献[15]中的方法,对点云数据实现全局格网划分,利用kd-tree构建点的局部邻域关系;②利用文献[2]中的方法计算各点的法向量nm。
1.3. 局部RANSAC在当前点云数据中随机抽取一采样点,根据其空间位置判定所属格网单元,在格网单元内部实施局部RANSAC方法,依次探测平面、柱面、球面模型的最优参数。算法过程如下:
(1) 模型计算:随机抽取m个必要采样完成各模型Mi参数计算。①平面:只需要一个有向采样(p, nm)即可确定一个平面Mp;②球面:以两采样点(p1, nm1)、(p2, nm2)确定两空间直线l1l2,以l1l2间的最短线段的中点o作为球的球心,以r=(‖p1-o‖+‖p2-o‖)/2为半径,确定球体参数Ms(o, R);③圆柱面:以两个采样点p1、p2的法向nm1、nm2的叉积作为圆柱的轴向dir,以p1、p2及其法向nm1、nm2确定两空间直线l1、l2,以l1、l2间的空间最短线段的中点o作为圆柱轴向所经过一点,确定轴线方程l(o, dir),以p1、p2至l(o, dir)的距离均值为半径r,确定圆柱Mc(o, r, dir)。
(2) 打分:在格网单元内对各模型Mi进行局部打分。依据如下两个规则,在局部格网单元中确定与所拟合模型Mi一致的点集数目,作为对应模型的打分。
① 法向约束
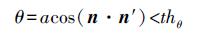 (1)
(1) 式中,n为采样点p的法向;n'为p点在模型Mi的投影点p'处的法向。
② 距离约束
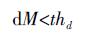 (2)
(2) 对于给定点P=(x, y, z),该点到平面ax+by+cz+d=0的距离dM可表达为
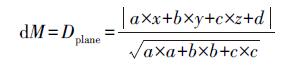 (3)
(3) 该点到球心坐标为Osp(a, b, c)球面方程(x-a)2+(y-b)2+(z-c)2=R2的距离dM可表达为
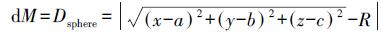 (4)
(4) 该点到中心轴向直线为L(x=x0+mt;y=y0+nt;z=z0+qt;P0=(x0, y0, z0))、底面半径为r的圆柱面距离dM可表达为
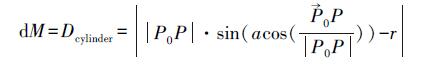 (5)
(5) 满足以上约束的点为模型的一致点。经过局部打分,确定各模型的最优参数及其一致集,对于一致集数目超过格网内部点数一半的最优模型Mi加入到候选模型集M中。
(3) 循环:循环以上过程,获得当前格网各基元最优模型,若各基元最优参数模型的一致集均小于预定数目,则重新采样;若通过,则将通过的各基元最优参数模型加入候选模型集M中,M=M∪Mi。
1.4. 确定最优模型若M中只有一种模型,则直接计算其全局一致集。若M中存在多种模型(例如在一定的误差范围内,柱面或球面的局部可能被认为是平面特征),则需进一步区分。理论上说,M中的最优模型,需要在全局范围内具有最大一致集,但在海量点云数据中,即使对平面特征打分,仍需要较大的时间开销。在数理统计中,常常通过抽样来推测具有某一特征的样本所占的总体比例,当抽样属于不放回抽样且当样本空间较大,可用正态分布来模拟描述该特性的随机变量的分布特征,在当前格网单元及其邻域单元中,判定某个点pti是否属于某个模型的过程可描述为
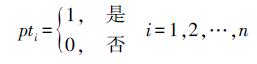 (6)
(6) 若在n个采样中有m个点满足该数学模型,则满足该模型的点占总体点云数据的比例P的数学期望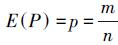
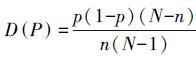
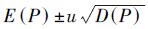
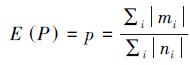
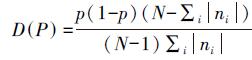
为了验证本文算法的有效性,以富含平面、柱面、球面特征的建筑物立面数据作为试验数据,如图 1所示,该数据点数为3 734 518,平均点间距为5 mm。算法实施采用单PC环境,内存配置为8 GB,CPU为i7-2760QM,主频为2.4 GHz。操作系统环境为Windows 7 64 bit专业版,算法采用C++语言,以VS.NET2010为平台。

|
| 图 1 建筑物点云数据 |
在数据预处理中,为保证格网单元有足够的样本空间,格网间距一般设为40倍的平均点间距;计算法向的邻域点数为25。在局部RANSAC算法中最大迭代次数为10 000;法向偏差阈值thθ可以根据面片邻接情况设置,相邻面片间存在较大突变可以设较大阈值,当面片间变换比较平缓,需设置较小阈值,设thθ=0.9 rad;距离阈值thd一般与仪器测距精度、多站配准精度和表面精细程度有关,本文统一设为2 cm。最小点集数目可以根据实际灵活设置,数目较大时较小面片就会被忽略,数目较小时则会保留较多的微小面片,本文统一设为50。
当随机采样点落在格网单元E中时,如图 2所示,在E中利用RANSAC方法探测平面、柱面、球面的最优参数模型,各参数模型在E中及各邻域格网的内点数目见表 1。可以看出,在E格网内,球面与柱面一致集相同且与平面类差别不大,基于统计推断的置信区间区分也不明显,见表 2。为了获得可靠的模型参数,在E格网的邻域格网中随机选取一格网,继续打分推断,设该随机选取的格网为D格网,各参数模型在各格网的累计打分和置信区间见表 2。由表可以看出,柱面的置信区间明显高于平面和球面,因此可以判定柱面为格网E中探测到的最优模型。同理,若该邻域格网为非D的其他格网,表 1给出了各邻域格网的打分统计,依然可以利用该方法获得当前最优模型。
| 格网 | 样本数 | 内点数 | ||
| 平面 | 柱面 | 球面 | ||
| A | 1373 | 6 | 1230 | 538 |
| B | 1250 | 1243 | 1250 | 292 |
| C | 1435 | 61 | 1435 | 606 |
| D | 1483 | 49 | 1349 | 305 |
| E | 1366 | 1343 | 1366 | 1366 |
| F | 1516 | 81 | 1516 | 349 |
| H | 1812 | 63 | 1451 | 611 |
| I | 1423 | 1422 | 1423 | 273 |
| J | 1618 | 124 | 1618 | 653 |
| 格网 | 总样本 | 总内点 | 期望 | 标准差 | 置信区间(置信度0.95) |
| E | 1366 | 平面:1343 柱面:1366 球面:1366 | 0.983 163 1 1 | 0.003 482 0 0 | [0.976 338 165, 0.989 987] [1,1] [1,1] |
| D | 2849 | 平面:1392 柱面:2715 球面:1671 | 0.488 592 0.952 966 0.586 522 | 0.009 363 0.003 966 0.009 224 | [0.470 240 746, 0.506 944] [0.945 193 373, 0.945 193] [0.568 441 988, 0.604 601] |

|
| 图 2 多几何面片探测 |
根据获得的最优模型,在全局点云中,根据式(1) —式(5) 的判定规则,计算该模型的内点,从而将该面片从点云数据中分割出来。但是在该过程中存在过度分割和分割不充分的问题:
第一种是在点云数据分割过程中,由于不同面片的分割顺序不同且允许误差的存在(点到模型的距离),在两相邻面片中会存在后分割面片中的点被误分割到相邻先分割的面片中,如图 3(a)所示,A、B、D为三相邻面片,由于面片A比面片B、D先分割出来,由于距离误差阈值的限制,面片B、D中到面片A的距离小于阈值的点被误分到面片A中,如图 3(a)所示C、E区域,因此A存在分割不充分,B存在过度分割,这些都属于误分割。而相邻面片交界处一般存在法向突变,因此本文的法向约束能较好地处理这类问题,约束后的分割效果如图 3(b)所示。

|
| 图 3 法向约束分割效果 |
另外一种是同参异面的情况,也就是某一参数模型的一致集存在不同面片聚集区域,如图 4(a)所示,这属于分割不充分的问题。因此对各模型的一致集进行空间聚类,将各聚类结点归为不同分割对象。对于平面类将其一致集投影至对应平面上,然后进行二维格网划分,按照常规聚类方法实现空间划分;柱面类面片需要按轴向展成平面,然后按照平面类方法进行共面分割;球面类按三维空间格网进行空间划分,实现共面分割。格网间距设为平均分辨率的4倍。共面分割和最终分割效果如图 4(b)所示。

|
| 图 4 共面分割效果 |
本文介绍了一种激光点云数据多种面片特征识别方法。该方法利用地面激光点云数据的高空间分辨率的特性,认为采样点是对目标对象的冗余表达,基于此提出基于局部采样的局部RANSAC模型探测方法,并利用统计推断策略估算各局部候选模型的全局打分,获得当前最优模型。该方法在采样策略上对传统RANSAC方法进行了优化,利用统计推断的策略对获得最优模型的方法进行了拓展。
试验结果表明,本文所提出的基于局部采样和统计推断的方法能够有效规避传统RANSAC方法的全局采样策略所造成的无法检测多种几何面片特征的问题,能够有效探测人工构筑物中存在的平面、柱面、球面特征,并且较好地处理了点云数据分割中的过度分割和分割不充分的问题、同参异面问题。
| [1] | 郭明.海量精细空间数据管理技术研究[D].武汉:武汉大学,2011. http://cdmd.cnki.com.cn/Article/CDMD-10486-1015535071.htm |
| [2] | RABBANI T.Automatic Reconstruction of Industrial Installations Using Point Clouds and Images[D].Delft:Delft University of Technology,2006. |
| [3] | 何文峰.大型场景三维重建中的深度图像配准[D].北京:北京大学,2004. http://d.wanfangdata.com.cn/Thesis/Y634755 |
| [4] | 陈卓, 马洪超. 基于机载LiDAR数据的大型立交桥自动提取与建模方法[J]. 测绘学报, 2012, 41 (2) : 252–258. |
| [5] | SITHOLE G,VOSSELMAN G.Filtering of Airborne Laser Scanner Data Based on Segmented Point Clouds[C]//Laser Scanning 2005.[S.l.]:ISPRS,2005. |
| [6] | TAMAS L, GORON L C. 3D Semantic Interpretation for Robot Perception Inside Office Environments[J]. Engineering Applications of Artificial Intelligence, 2014, 32(4-5): 210–215. |
| [7] | BELTON D. Classification and Segmentation of 3D Terrestrial Laser Scanner Point Clouds[D]. Bentley:Curtin University of Technology,2008. |
| [8] | 李宝.三维点云的鲁棒处理技术研究[D].长沙:国防科学技术大学,2011. http://cdmd.cnki.com.cn/article/cdmd-90002-1011303382.htm |
| [9] | BOLLES R C,FISCHLER M A.A RANSAC-based Approach to Model Fitting and Its Application to Finding Cylinders in Range Data[C]//Proceedings of the 7th International Joint Conference on Artificial Intelligence.[S.l.]:International Joint Conference on Artificial Intelligence,1981,637-643. http://www.opticsjournal.net/abstract.htm?id=OJ130116000163PlSoUr |
| [10] | CHAPERON T, GOULETTE F. Extracting Cylinders in Full 3-d Data Using a Random Sampling Method and the Gaussian Image[J]. VMV, 2001(1): 35–42. |
| [11] | 王植, 李慧盈, 吴立新, 等. 基于RANSAC模型的机载LiDAR数据中建筑轮廓提取算法[J]. 东北大学学报(自然科学版), 2009, 33 (2) : 271–275. |
| [12] | 皇甫中民, 闫雒恒, 刘雪梅. 基于RANSAC算法的旋转面特征提取[J]. 计算机工程与设计, 2009, 30 (5) : 1295–1298. |
| [13] | TAREK M A.基于散乱地面激光扫描点云数据的复杂立面中平面的自动提取[D].武汉:武汉大学,2010. http://cdmd.cnki.com.cn/Article/CDMD-10486-2010166939.htm |
| [14] | 陈付幸, 王润生. 基于预检验的快速随机抽样一致性算法[J]. 软件学报, 2005, 16 (8) : 1431–1437. |
| [15] | 王力. 三维扫描数据处理中数据结构的设计与比较[J]. 测绘通报, 2010 (9) : 63–65. |


