近年来三维激光扫描仪已经成为测绘科学和计算机领域中的研究热点,并且越来越广泛地应用于各种测绘工程项目中[1-3]。与传统测量手段相比,三维激光扫描仪在获取点坐标时不再以单点方式进行,可以一次性大量扫描待测物体表面的点云,并且数据的处理及建模也较为简单[4-6]。但是由于三维激光扫描仪每个测站获取的点云都是以当前位置为原点,即每个测站点云的原始坐标系统都是独立的,因此需要经过点云拼接才可以获得具体某一坐标系统下的成果。此外,不同测站间的点云进行高精度的拼接可以提高最终成果的精度,因此,开展三维激光扫描仪不同测站的点云拼接分析具有非常重要的意义。
三维激光扫描仪不同测站间常用的拼接方法是采用球形标靶完成。不同数量的标靶及不同的分布情况均会对点云拼接精度产生影响,但目前国内这方面的研究还较少,大部分学者侧重于点云拼接算法方面的研究[7-12],少部分学者对三维激光扫描仪的各种指标进行试验分析[13-15]。为此,本文开展了针对不同标靶数量和不同标靶分布情况的点云拼接试验,并通过大量试验的对比分析得出标靶更加合理、有效、经济的配置方案。结果表明,通过合理的标靶配置能提高整个测区的点云拼接精度。
1、 基于球形标靶的点云拼接原理球形标靶是点云拼接过程中常用的辅助工具。基于球形标靶的点云拼接原理主要包括球形标靶的球心拟合和空间直角坐标边缘两部分。
1.1. 球心拟合球形标靶经过扫描后可以获取大量的扫描点,球心的三维坐标需要通过对这些点进行拟合得到。假设球心坐标为(x, y, z),球形标靶半径为r,扫描点三维坐标分别为(xi, yi, zi),其中i为扫描点个数(i=1, 2, …,n),可以得到球心位置、球形标靶半径和离散点间的函数关系为
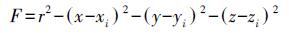 (1)
(1) 显然,式(1) 为非线性方程,需要进行线性化,即泰勒级数展开才可以求解球心位置和球形标靶的半径。将式(1) 线性化并求解各项偏导数,整理得到单个离散点的误差方程为
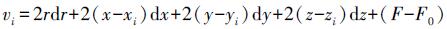 (2)
(2) 建立所有球形标靶表面扫描点的误差方程并写成矩阵形式为
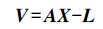 (3)
(3) 式中
在本文处理过程中,每个离散点均按照等权重情况来处理,则根据最小二乘原理可以求解得球心三维坐标和球形标靶的半径
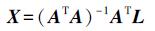 (4)
(4) 获取不同测站间的连接点即球心坐标后,即可进行离散点云的空间直角坐标融合转换。传统空间直角坐标变换时一般采用七参数模型进行转换,即3个旋转角(φ, ω, κ)、3个平移量(X0, Y0, Z0)和1个尺度缩放因子[16]。由于点云拼接一般针对同一台扫描仪的不同测站点云开展,因此,本文的空间直角坐标变换采用六参数模型,即舍弃了尺度缩放因子。具体模型为
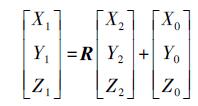 (5)
(5) 式中,(X1, Y1, Z1)为转换后的坐标;(X2, Y2, Z2)为原始坐标;R为3×3阶的标准旋转正交矩阵。
在转换参数未知的情况下需要首先根据上述模型进行转换参数的求解。很显然,式(5) 为非线性方程,需要将其进行线性化后才能实现转换参数求解。根据上述模型建立误差方程为
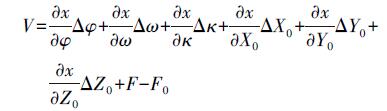 (6)
(6) 在上述误差方程的基础上,通过迭代求解即可得到6个转换参数。进行不同测站点云拼接即可实现不同测站点云的空间直角坐标转换。
2、 试验及分析为了研究标靶数量和分布对点云拼接的影响,开展了多组试验,并对拼接结果进行了分析。
2.1. 试验方案设计本文分别设计了近距离和远距离两种状态下的不同标靶分布的点云拼接试验。方案如下:
(1) 球形标靶基本处于同一高度,并在两测站间不规则地随机分布,三维激光扫描仪从标靶放置区中心左右两侧20 m和40 m附近进行扫描。20 m距离条件下的标靶放置如图 1所示,40 m时与其类似。

|
| 图 1 标靶同高离散分布示意图 |
(2) 球形标靶在不同高度下,在两测站间不规则地分布,扫描仪从标靶放置区中心的两侧距离大约20 m和40 m处扫描。标靶放置与图 1类似。
(3) 球形标靶基本处于同一高度,并在两测站间较为规则地分布,扫描仪从标靶放置区中心左右两侧大约20 m和40 m处扫描。20 m时的标靶放置如图 2所示,40 m时与其类似。

|
| 图 2 标靶同高规则分布示意图 |
(4) 球形标靶处于不同高度,并在测站间较规则地分布,扫描仪从标靶放置区中心左右两侧大约20 m和40 m处扫描。标靶放置与图 2类似。
2.2. 点云拼接试验针对上述试验方案,分别研究了标靶上的扫描点数量、作为连接点的标靶数量、连接标靶分布及扫描距离对拼接精度的影响。开展的试验均采用FARO FOCUS 3D扫描仪进行,扫描参数为点距离1.53 mm/10 m;扫描尺寸为9103×6827像素;在扫描质量最高的情况下进行数据采集。
2.1.1. 扫描点个数对拼接精度的影响为了研究扫描点数量对拼接精度的影响,在标靶分布不变的情况下,采用了点距离分别为(a)1.53 mm/10 m、(b)3.07 mm/10 m、(c)6.14 mm/10 m的3种分辨率开展扫描,并对采用相同标靶进行拼接的结果进行了分析。表 1为点距离逐渐增加的3次扫描结果。
| 个 | ||||||||
| 标靶编号 | (a) | (b) | (c) | |||||
| 左测站 | 右测站 | 左测站 | 右测站 | 左测站 | 右测站 | |||
| 1 | 1672 | 236 | 1131 | 264 | 386 | 68 | ||
| 2 | 900 | 316 | 629 | 288 | 248 | 80 | ||
| 3 | 1136 | 324 | 831 | 291 | 367 | 72 | ||
| 4 | 816 | 376 | 647 | 338 | 264 | 89 | ||
| 5 | 536 | 536 | 453 | 423 | 148 | 164 | ||
| 6 | 460 | 544 | 418 | 416 | 185 | 148 | ||
| 7 | 500 | 612 | 432 | 409 | 154 | 157 | ||
| 8 | 380 | 848 | 356 | 617 | 136 | 300 | ||
| 9 | 280 | 1304 | 284 | 897 | 62 | 304 | ||
| 10 | 260 | 1692 | 264 | 1162 | 72 | 336 | ||
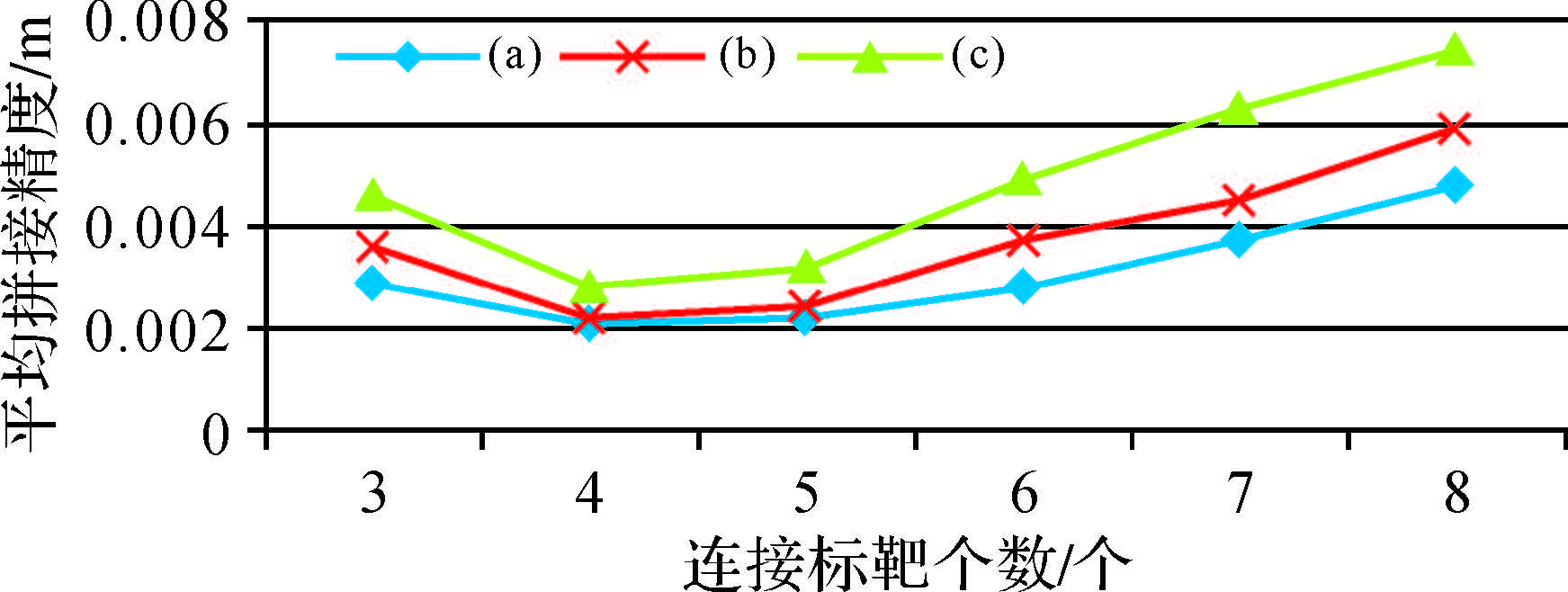
分别从上述10个标靶中选取扫描点数量较多的标靶开展(a)、(b)、(c)3种扫描点距条件下的拼接试验,得到3~8个连接点下的平均拼接精度,如图 3所示。
|
| 图 3 不同扫描点下的拼接精度 |
此外,以3个球形标靶为例,研究了在不同数量扫描点下的拼接误差,如图 4所示。
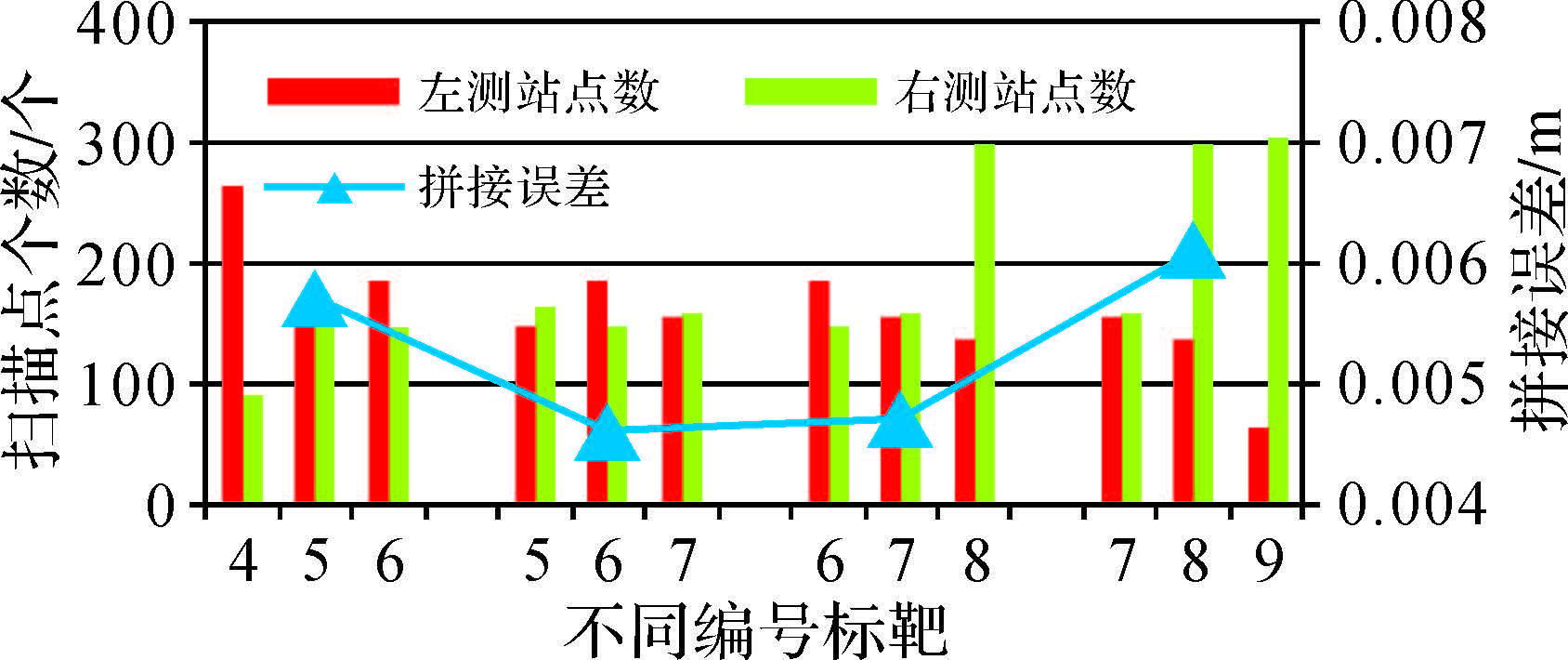
|
| 图 4 3个连接标靶点的拼接精度 |
由表 1和图 3可得,以平均拼接精度最高时的4个连接点(5、6、7、8号作为连接标靶)为例,当扫描点距离小时,左右测站获取的扫描点数量大致相当,平均扫描点为552个,平均拼接误差为2.1 mm;当扫描距离逐渐增大时,平均扫描点数量降低至440和174,平均拼接误差增大至2.2 mm和2.8 mm。当连接标靶数量改变时,情况类似。
由图 4可知,选择5、6、7号标靶和6、7、8号标靶进行拼接时,得到的拼接误差大致相当,且都比较小,而选择4、5、6号标靶和7、8、9号标靶作为连接点时,拼接误差明显增大。因此,可认为当所选择的连接标靶中存在扫描点较少的标靶时,拼接精度明显降低;两测站扫描点数量大致相当且数量较多时,得到的拼接误差最小。
2.2.2. 连接标靶数量对拼接精度的影响本文研究了球形标靶在相同高度规则排列(a)、不同高度规则排列(b)、相同高度不规则排列(c)、不同高度不规则排列(d)4种情况下的布置对拼接精度的影响(以下过程中均以(a)、(b)、(c)、(d)分别对应上述4种标靶分布情况)。此外,尽可能采用扫描点数量多的标靶进行拼接以消除扫描点数量的影响。图 5为标靶布置区中心与扫描仪距离大致为20 m和40 m时,不同连接点下的拼接精度。
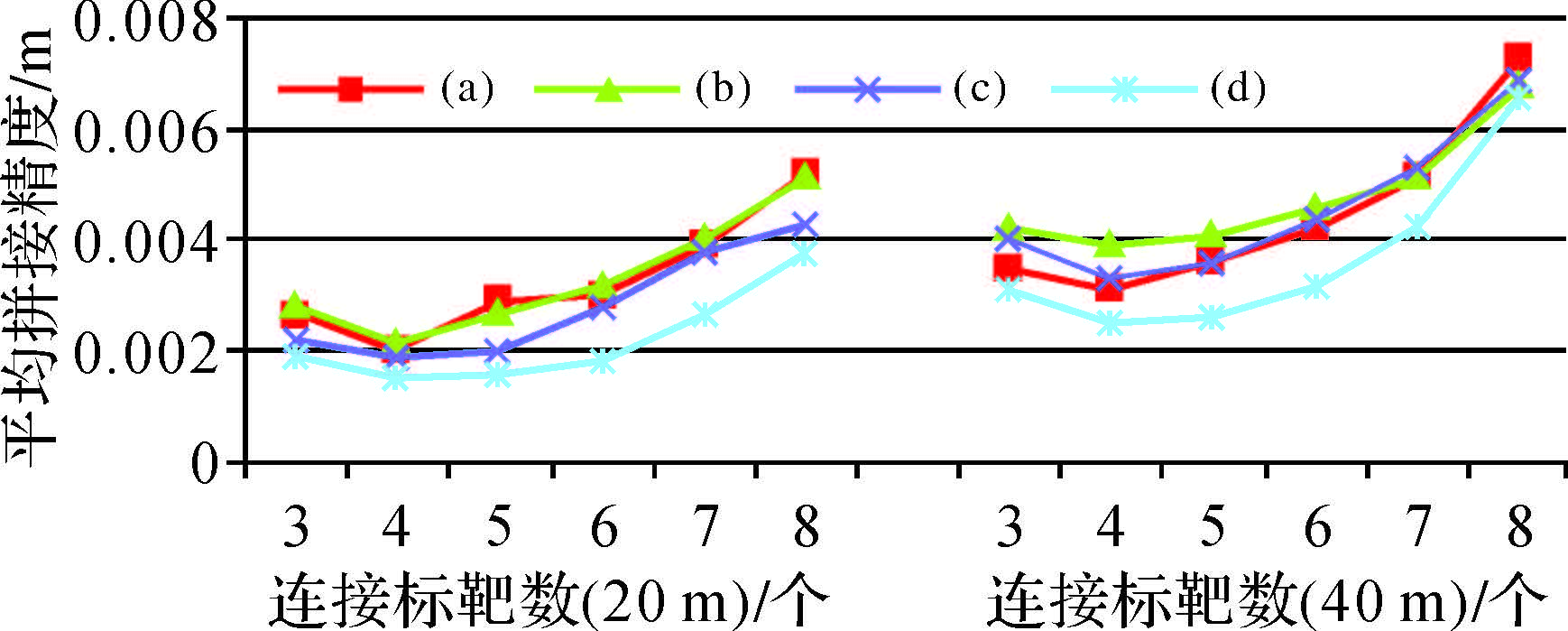
|
| 图 5 20 m时不同连接点的拼接误差 |
由图 5可得,在20 m条件下,当拼接点数量为3个时,4种分布的拼接误差较大;连接点数量为4~5个时,拼接误差较小;而连接点数量大于5个且逐渐增加时,拼接误差均明显增大。在40 m条件下,当拼接点数量为3个时,4种分布的拼接误差较大;连接点数量为4个时,拼接误差最小;而连接点数量为5个时,标靶不同高度不规则排列的拼接精度与4个时差别较小,而其他分布的拼接误差明显增大。当连接标靶大于5个时,拼接误差增大趋势更加明显。
为了消除标靶分布因素的影响,对上述4种标靶布置时的拼接精度求平均值,如图 6所示。
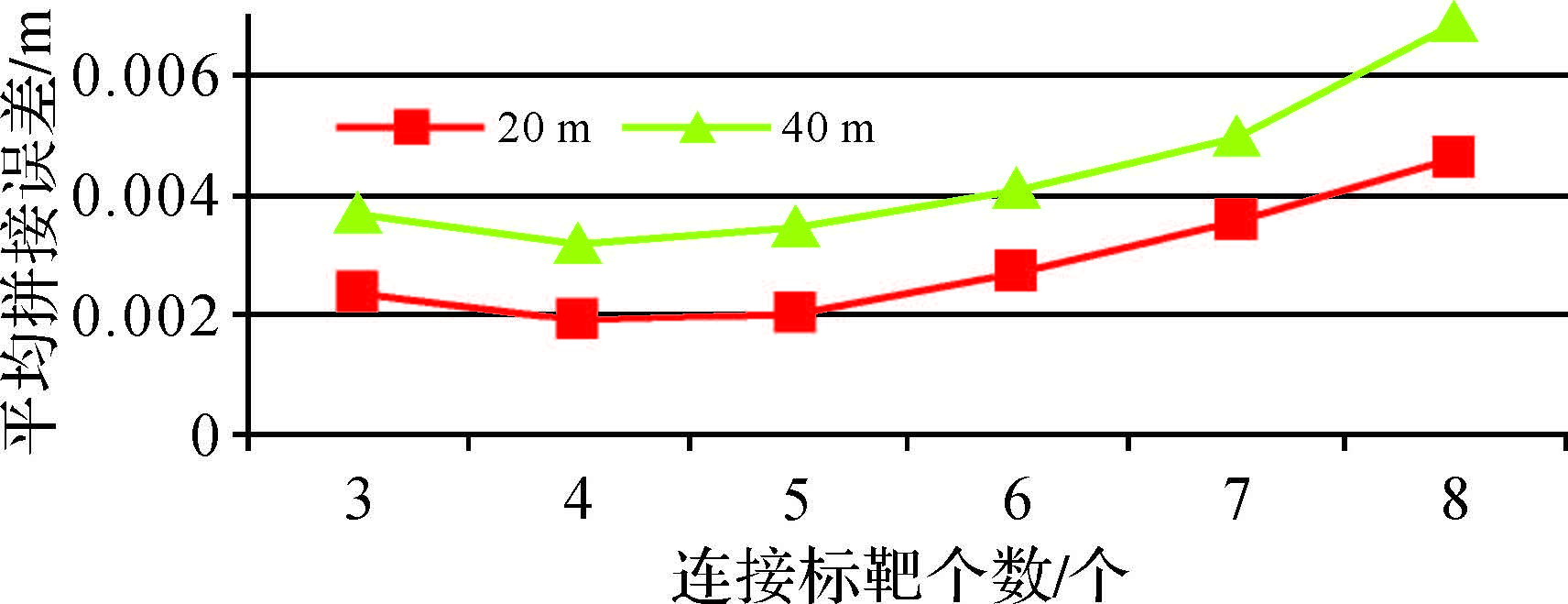
|
| 图 6 不同数量连接点对拼接精度的影响 |
由图 6可得,20 m条件下,当连接点数量分别为4、5、3、6、7、8个时,平均拼接误差分别为1.8、2、2.4、2.7、3.6、4.6 mm;40 m条件下的情况类似。
2.2.3. 标靶分布对拼接精度的影响本文研究了20 m和40 m条件下上述4种标靶布置对拼接精度的影响。图 7为4、6和8个连接点时两种距离条件下的平均拼接误差。
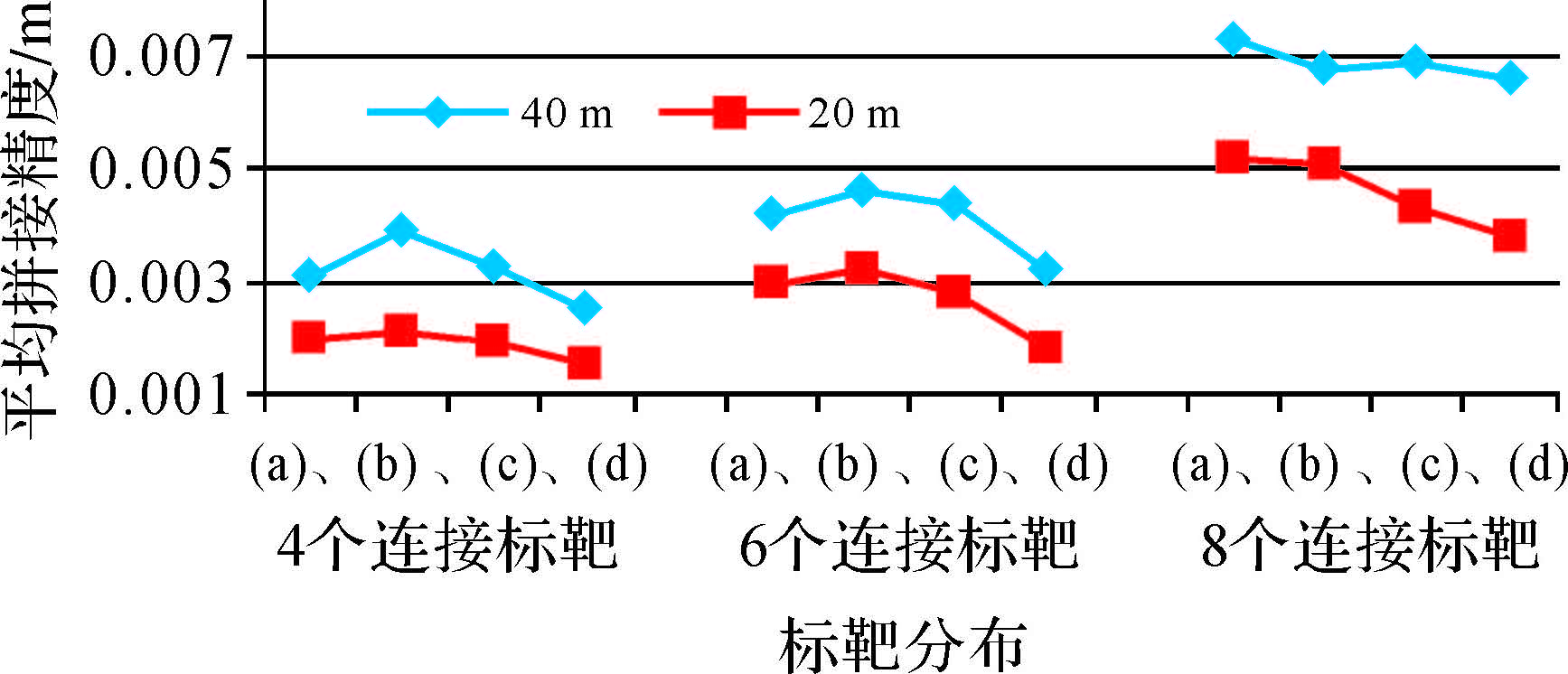
|
| 图 7 不同连接点的不同分布拼接误差 |
由图 7可得,在距离和标靶点数量相同时,拼接精度与标靶分布密切相关。在不同连接点数量和相同扫描距离时,标靶在不同高度不规则排列时的拼接误差均为最小。
对4、6和8个连接点在4种情况下的拼接误差求平均并进行统计,统计结果见表 2。
| m | ||||
| 标靶分布 | 相同高度规则排列 | 不同高度规则排列 | 相同高度不规则排列 | 不同高度不规则排列 |
| 20 | 0.003 15 | 0.003 22 | 0.002 85 | 0.002 22 |
| 40 | 0.004 47 | 0.004 78 | 0.004 58 | 0.003 72 |
由图 7和表 2的统计结果可见,相同连接点数量和相同距离时,标靶在规则排列的两种情况下的拼接精度都低于不规则排列的两种,且不规则排列情况下,相同高度不规则排列分布时的平均拼接误差较大,标靶在不同高度不规则排列分布时的平均拼接误差均为最小。
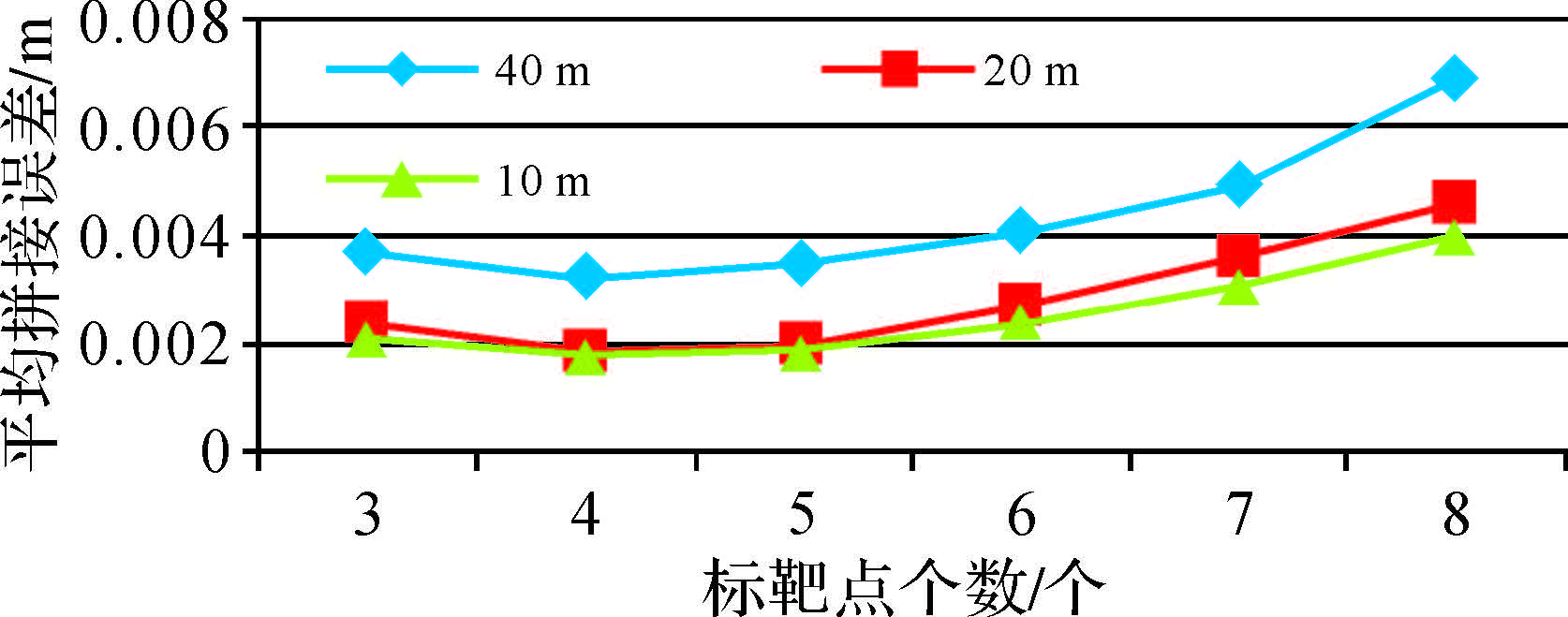
2.2.4. 距离对拼接精度的影响将三维激光扫描仪放置于标靶区中心位置左右两侧距离大约10、20和40 m的位置,进行上述4种情况下的布置后开始扫描。随后对不同距离情况,采用3~8个连接点开展拼接试验,并对4种分布情况的拼接误差求平均,然后进行统计(消除分布带来的影响),得到误差如图 8所示。
|
| 图 8 不同距离对拼接精度的影响 |
由图 8可得,距离对不同测站点云拼接精度影响较大。在不同标靶点数量下,标靶布置区域离扫描仪越近,得到的拼接结果误差均比较小,而离扫描仪越远,得到的拼接结果误差均比较大。表 3为不同距离下的拼接误差统计结果。
| m | |||
| 距离 | 最大误差 | 最小误差 | 平均误差 |
| 10 | 0.004 | 0.001 8 | 0.002 6 |
| 20 | 0.004 6 | 0.001 9 | 0.002 9 |
| 40 | 0.006 9 | 0.003 2 | 0.004 4 |
由表 3可得,当距离由10 m变为20 m时,拼接结果的最大误差仅差0.6 mm,最小误差仅差0.1 mm,平均误差仅差0.3 mm,可认为距离小于20 m时,当扫描设置相同的情况下,距离对拼接精度的影响很小。但是当距离由20 m变为40 m时,拼接结果的最大误差相差2.3 mm,最小误差相差1.3 mm,平均误差相差1.5 mm。
2.3. 结果分析开展了针对上述4种影响因素的试验后,在对误差进行统计的基础上,分别针对单个因素进行了分析并得到以下结果:
(1) 扫描点数量越多,拼接精度越高。这是由于扫描点的数量会影响到球形标靶的球心坐标拟合精度,当扫描点数量非常多时,拟合得到的球心精度较高;当扫描点数量较少时,拟合得到的球心坐标精度有限,进一步影响到坐标系统转换过程中的变换参数的精度,因此,拼接点云数据时应优先选择扫描点数量均衡且较多的标靶作为连接点,即尽量选择位于两测站中间区域的标靶作为连接点。
(2) 当取4~5个标靶作为连接点时,点云的拼接精度最高,而连接点数量降低至3个或增加到5个以上时,不同测站点云的拼接精度均有所降低。这是由于采用3个连接点时,多余观测数据有限,导致坐标转换过程的参数求解精度较低;当连接点增加到5个以上时,由于部分标靶扫描点数量减小导致拟合的球心精度降低,从而增大了拼接误差;当连接点选择4~5个时,球形标靶的球心拟合精度较高,而且存在多余观测,坐标转换参数的求解精度也比较高,因此,得到的点云拼接精度最高。
(3) 不同连接点条件下,标靶不规则排列的精度整体高于规则排列的精度;规则排列情况下,高程对拼接结果的影响不大,而在不规则排列情况下,当标靶处于不同高度时的点云拼接精度明显优于标靶基本处于同一高度的情况。这是由于当标靶规则排列时,观测值中标靶的平面坐标可能存在较强的相关性,而不规则排列但高程基本处于同一平面时,观测值中标靶的平面坐标虽然不相关,但高程信息可利用程度不高,导致坐标转换参数的求解出现误差;而标靶处于不同高度不规则排列时,观测值中的三维坐标不相关,因此求解得到的坐标转换参数精度最高。
(4) 当距离为10 m和20 m时,点云的拼接精度差别不大,但是当距离增加到40 m时,拼接误差有明显增大的趋势。这是由于扫描距离由10 m变为20 m时,扫描点数量虽然有所减少,但仍比较多,拟合得到的球心坐标精度较高;当距离增大到40 m时,扫描点数量出现明显减少,得到的球心坐标精度降低,最终影响到拼接的精度。
综上所述,影响点云拼接精度最重要的因素是标靶扫描点的数量和标靶的分布,扫描点数量会影响到球形标靶的球心坐标拟合精度,而标靶的分布和数量会影响到坐标转换参数的求解精度。因此,当标靶上扫描点的数量较多时,最好选择不规则排列的4~5个标靶作为连接点,这样得到的拼接精度最高,当扫描点数量不足时,最好采用4个标靶作为连接点,这样得到的拼接结果较好。
3、 结束语本文研究了球形标靶扫描点数量、作为连接点的标靶数量、标靶分布及标靶布置区与扫描仪之间的距离这4个因素对于不同测站点云数据拼接的影响。大量试验表明,标靶上的扫描点数量和标靶分布是影响拼接精度的主要因素,在点云拼接时应尽量选择扫描点数多,并且标靶布置区左右两测站的扫描点数量大致相同时为最优。标靶分布为不同高度不规则排列时,点云拼接精度最高。对于连接点数量因素,作为连接点的标靶数量为4~5个时拼接误差最小。此外,当扫描距离增大时,标靶上的扫描点数量会减少,也会影响到拼接精度。综合各项因素的影响,当两测站的标靶上的扫描点数量大致相等,取4~5个标靶作为连接点且放置在不同高度不规则排列时,拼接效果最优。本文研究可以为大范围高精度三维建模提供参考。
| [1] | 熊友谊, 冯志新, 陈颖彪, 等. 利用点云数据进行三维可视化建模技术研究[J]. 测绘通报, 2015 (2) : 20–23. |
| [2] | 李明磊, 李广云, 王力, 等. 3D Hough Transform在激光点云特征提取中的应用[J]. 测绘通报, 2015 (2) : 29–33. |
| [3] | 托雷, 康志忠, 谢远成, 等. 利用三维点云数据的地铁隧道断面连续截取方法研究[J]. 武汉大学学报(信息科学版), 2013 (2) : 171–175. |
| [4] | 罗德安, 朱光, 陆立, 等. 基于三维激光影像扫描技术的整体变形监测[J]. 测绘通报, 2005 (7) : 40–42. |
| [5] | 原玉磊, 骆亚波, 郑勇. 三维激光扫描仪在抛物面天线测量中的应用研究[J]. 测绘通报, 2012 (2) : 48–51. |
| [6] | 刘慎栋, 张成林, 徐耀汉, 等. 三维激光扫描仪在土方量估算中的应用[J]. 测绘通报, 2015 (10) : 135–136. |
| [7] | 闫利, 曹亮, 陈长军, 等. 车载全景影像与激光点云数据配准方法研究[J]. 测绘通报, 2015 (3) : 32–36. |
| [8] | 周朗明, 郑顺义, 黄荣永. 旋转平台点云数据的配准方法[J]. 测绘学报, 2013, 42 (1) : 73–79. |
| [9] | 辛伟, 普杰信. 点到邻域重心距离特征的点云拼接[J]. 中国图象图形学报, 2011, 16 (5) : 886–891. |
| [10] | 郑敏辉, 臧玉府, 梁福逊, 等. 不同场景的地面激光点云配准方法研究[J]. 测绘通报, 2015 (3) : 30–34. |
| [11] | 汪开理. 三维激光点云与全景影像匹配融合方法[J]. 测绘通报, 2013 (12) : 130–131. |
| [12] | 杨荣华, 吕美英, 花向红. 一种多站标靶点云整体配准算法[J]. 武汉大学学报(信息科学版), 2014, 39 (10) : 1189–1193. |
| [13] | 王冬, 卢秀山, 张占杰. RIEGL LMS-Q140i-80激光扫描仪精度评定[J]. 测绘科学, 2006, 31 (5) : 115–119. |
| [14] | 官云兰, 程效军, 詹新武. 地面三维激光扫描仪系统误差标定[J]. 测绘学报, 2014, 43 (7) : 731–738. |
| [15] | 张永彬, 高祥伟, 谢宏全, 等. 地面三维激光扫描仪距离测量精度试验研究[J]. 测绘通报, 2014 (12) : 16–19. |
| [16] | 陈玮娴, 袁庆, 陈义. 约束总体最小二乘在点云拼接中的应用[J]. 大地测量与地球动力学, 2014, 31 (2) : 137–141. |