积累多年的GPS站坐标时间序列可以反映出测站的线性与非线性的运动特征,为地壳形变监测及一些地球物理现象的解释提供了宝贵的基础数据。然而有研究表明,GPS坐标时间序列中除含有非周期性误差外,还包含周期性误差[1],称之为虚假的周期性信号。这些周期性误差是由未模型化的系统性误差(包括由地球物理因素引起的误差、系统误差、GPS数据处理中采用的计算方法的误差)传播到GPS坐标时间序列中生成,其周期范围为两个星期至一年[2-3]。这些周期性及非周期性的误差严重影响着对测站运动状态的分析,且会导致对引起测站非线性变化的地球物理因素的错误解释[3-4],因此有必要采取措施削弱其对GPS站坐标时间序列分析的影响。
由于共模误差(common mode error, CME)被认为是GPS站坐标时间序列误差的主要来源之一[5],因此许多研究通过去除CME来削弱噪声的强度,提高坐标时间序列的信噪比[6-9]。此外,由于小波变换可以通过对信号的高频分解系数进行阈值量化去除噪声,因此也被用于GPS站坐标时间序列分析,具有较好的去噪效果[12-13]。以上方法有效地削弱了噪声对GPS坐标时间序列的影响,但仍存在一些不足。首先,小波变换无法分辨和剔除GPS坐标时间序列中包括周年及半周年在内的长周期性误差。其次,去除CME仅可以剔除区域GPS站坐标时间序列所受的共同的误差影响,但在每个测站剩余的时间序列中依然存在较强的噪声。由于CME很可能是由未模型化或未完善的卫星轨道误差、参考框架误差、地球定向参数误差造成的,且未完善的接收机和卫星天线相位中心误差以及大尺度的大气影响也是共模误差的潜在来源[5],因此CME与周期性误差具有共同的误差源。根据以上分析,本文结合这两种方法的优点,首先通过区域叠加滤波法去除GPS站坐标时间序列中的CME,以此削弱周期性误差;然后对滤波后的时间序列进行小波分解,并提取周年及半周年信号,最后获得具有较高信噪声比的时间序列。
1 时间序列分析方法 1.1 区域叠加滤波法提取GPS站坐标时间序列中的共模误差可以去除测站相同分量时间序列之间的相关性,提高时间序列的信噪比[7]。由于本文所选择的GPS测站之间的距离不超过500 km,因此利用区域叠加滤波法去除共模误差[14]。该算法假设共模误差在某一区域是均匀分布的,将单日解的误差作为权重因子,利用简单的算数平均计算共模误差[7]
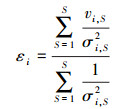 (1)
(1) 式中,εi为第i个历元的共模误差值;v为残差坐标时间序列;σi, S为单日坐标解的误差;S为参与计算共模误差的站台数。其中,v通过去除坐标时间序列的线性趋势以及周年和半周年谐波获得。
1.2 静态离散小波变换小波变换是一种时频局部化方法,具有多分辨率分析的特点,可以探测信号中的瞬态成分及频率成分,因此被称为数学显微镜。小波变换主要包括连续小波变换和离散小波变换。在实际问题的数值计算中常采用离散形式,即离散小波变换(discrete wavelet transform, DWT)。小波分析相关公式如下
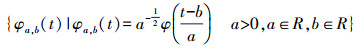 (2)
(2) 式中, φ(t)为小波母函数,对其进行平移和伸缩得到小波基函数集φa, b(t); a为尺度因子; b为平移因子; R为实数集。通常取
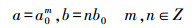 (3)
(3) 代入式(2)可得
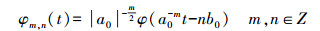 (4)
(4) 此时离散小波变换公式为
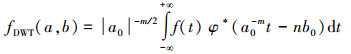 (5)
(5) 式中,fDWT(a, b)为连续小波变换系数;*表示共轭。一维离散小波变换实现的算法一般是Mallat算法,即先对较大的信号进行小波变换,获得近似系数和细节系数,再选取近似系数在原尺度的1/2尺度上进行小波变换。其中每次小波分解都进行下采样,只保留偶数项,因此每次离散小波变换所获得的小波系数的长度为上一次小波变换系数长度的一半,且丢弃了奇数项所含的时移信息。根据采样定理,为获得包含周年及半周年信号的小波系数,本文需对GPS站坐标时间序列至少分解为8层。因此,若利用离散小波变换,坐标时间序列的长度至少为28。为解除离散小波变换层数对坐标时间序列长度的限制,获得包含全部时移信息的小波系数,本文采用静态离散小波变换(static discrete wavelet transform, SWT)。在对信号的分解过程中,SWT不对分解的系数进行下采样,因此每次分解得到的系数长度都与原信号相同。在信号重建过程中,近似系数和细节系数分别作用重建低通和高通滤波后,直接相加就可以得到重建的上一层次的近似系数(或原始信号)。
2 实例分析 2.1 GPS数据本文采用南加利福尼亚地区16个GPS测站2010—2016年的坐标时间序列(ftp://sideshow.jpl.nasa.gov/pub/usrs/mbh/point/)。这些测站是PBO(Plate Boundary Observation)核心网络的组成部分,具体位置如图 1所示。其坐标时间序列由JPL(Jet Propulsion Laboratory)利用PPP数据使用GIPSY软件生成的日解组成。JPL给出了剔除粗差后干净的时间序列,确定了阶跃并估计了测站的运动速度。在分析GPS站坐标时间序列之前,笔者根据JPL给出的阶跃估值对剔除粗差的时间序列进行改正。在日解处理过程中采用的改正模型如下:地球、太阳、月亮及其他行星的引力模型;DE421行星星历模型;IAU06岁差和章动模型;IERS21010潮汐模型;FES2004海洋负载模型;IGS卫星以及接收机天线相位中心模型。

|
| 图 1 GPS测站分布 |
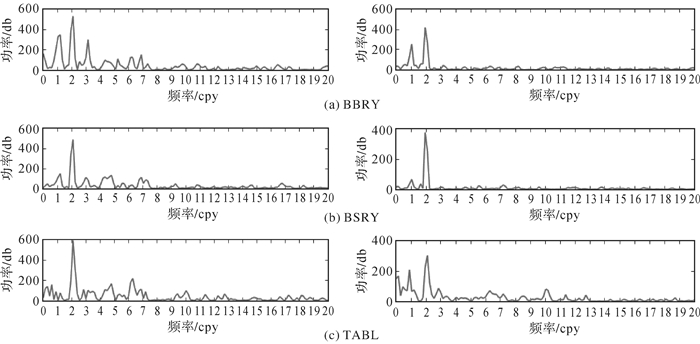
本文首先采用区域叠加滤波法去除GPS站坐标时间序列的共模误差。由于垂直方向时间序列的误差强度最大,受篇幅所限,本文仅列出BBRY、BSRY,以及TABL站垂向时间序列的分析结果。图 2为这3个测站垂直方向原始坐标时间序列以及去除共模误差后时间序列的功率谱。
|
| 图 2 垂向原始时间序列去除共模误差前后的功率谱 |
分析图 2可知,去除共模误差之前,BBRY与BSRY站垂向时间序列中皆含有明显的周年及半周年信号,而TABL站仅含有能量较强的半周年信号。此外,从图 2中还可以看出,原始时间序列中还含有众多能量弱于周年半周年的周期性误差。这些误差很可能是由地球物理效应及日解中的GPS系统误差造成的虚假周期信号。研究表明,未模型化的半周日和周日海潮负荷位移信号在GPS站坐标时间序列中产生了两星期、半年和周年周期信号[14]。理论计算表明,这种虚假的“潮汐分量”会对GPS时间序列产生垂向0.5~1 mm、水平向0.1~0.2 mm的偏差。同时GPS卫星的重复轨道周期也会引起混叠效应,在GPS站坐标时间序列中产生虚假的周期信号[15]。以上周期性误差会导致对地球物理信息的错误解释。
对比滤波前后信号的功率谱可知,滤波后BBRY与BSRY站垂向时间序列的周年和半周年信号的功率均有较大程度的下降,且BBRY站频率为3 cpy的周期信号基本上被消除。TABL站的半周年信号功率几乎减少一半,但其周年信号功率却大幅度增加。此外,频率大于2 cpy的周期性误差的功率也被大幅度削弱。由于共模误差主要包含与GPS相关的技术误差(如高阶电离层延迟、对流层延迟),以及包含少量的由其他地球物理因素(如海洋潮汐、大气潮汐及大气负载)造成的误差,且以上因素都能够对GPS站坐标时间序列中的周年及半周年信号造成不同程度的影响[16-17]。因此,共模误差序列中存在年周期信号、半年周期信号和其他周期性信号。通过去除共模误差削弱了GPS站坐标时间序列中包括周年及半周年误差在内的周期性误差的强度,致使GPS站坐标时间序列的周年和半周年信号的功率降低,还原了被掩盖的真实的周年及半周年信号的功率,提高了时间序列的信噪比。另外,从图 2还可以看出,滤波前后这3个测站半周年的功率皆大于周年,尤其BSRY站周年半周年的功率滤波后相差最大。根据JPL提供的这3个测站在垂直方向周年与半周年的正余弦系数可知,BSRY与TABL站在垂直方向的半周年振幅大于周年振幅,而BBRY站的周年振幅大于半周年,因此BSRY和TABL站垂向时间序列中半周年信号的功率也大于周年信号。对于BBRY站而言,在1998—2016年间其垂向时间序列中周年信号的振幅大于半周年信号,而在2010—2016年内半周年信号的振幅很可能大于周年信号,因此图 2中BBRY站半周年信号的功率大于周年信号。从图 2还可以看出,以上测站滤波后垂向时间序列的功率谱中仍存在未剔除干净的高频的周期性误差,如在TABL站的功率谱中,频率为3、10 cpy处仍存在功率为100 db的周期性误差。
周年、半周年信号是当今IGS全球基准站最主要的信号特征,而滤波后的时间序列中仍存在未剔除干净的较强的噪声。因此本文通过小波变换,将滤波后的时间序列中信号的不同频率成分分解到互不重叠的频带上,以此将周期为半周年以上的信号和噪声分开。首先剔除滤波后时间序列的性趋势,然后选用小波函数“coif5”,利用静态离散小波变换将其分解为8层。图 3-图 5为以上测站垂向时间序列各层的小波分解信号及其功率谱图。其中,d1—d8为对信号进行小波分解后得到的高频信号,包含了信号的细节信息;a8为第8层分解得到的低频信号,反映了信号的整体非线性运动特征。根据采样定理,d1—d8以及a8信号的主要频带范围分别是91.25~182.5、45.625~91.25、22.81~45.625、11.39~22.81、5.69~11.39、2.85~5.69、1.42~2.85、0.73~1.42及0~0.73。因此d7与d8层信号分别包含了周期为半周年与周年的周期信号。

|
| 图 3 BBRY站小波分解及各层功率谱 |
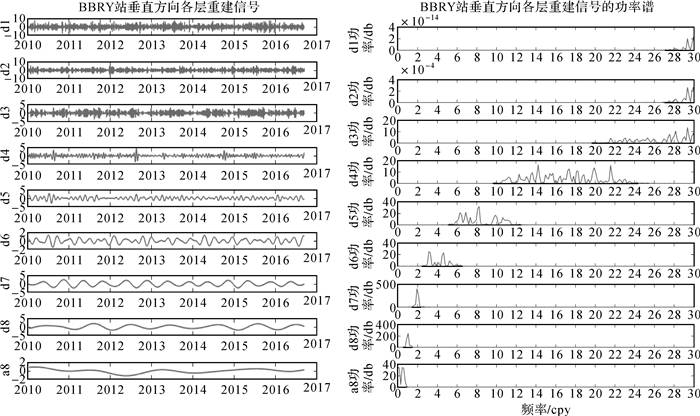
|
| 图 4 BSRY站小波分解及各层功率谱 |

|
| 图 5 TABL站小波分解及各层功率谱 |
从各层的重建信号及其相应的功率谱可以看出,在d1—d2层的28~30 cpy频带上存在功率不足1 db的周期性误差;d3、d4层分别在20~30 cpy以及10~24 cpy频带存在功率不超过20 db的周期性误差;d5、d6层分别在6~12 cpy以及2~6 cpy频带存在最大功率不超过40 db的周期性误差;在d7~d8层信号中存在较为明显的振幅均小于5 mm的周年及半周年信号,其功率分别为280和410 db,其中TABL与BSRY的周年振幅均小于2 mm。此外,在a8的功率谱中还存在功率较小但周期约为两年的信号。由于a8包含了原始信号中除线性趋势之外的总体趋势信息,考虑到信号的拟合度,本文对其予以保留。根据以上分析,本文利用小波逆变换提取含有周期大于半周年的d7、d8以及a8信号,舍弃包含高频误差的d1—d6信号,最后将提取出的信号与最初从原始时间序列中剔除的线性趋势信号相加,获得具有较高信噪比的时间序列。
为进一步比较滤波与小波变换后曲线拟合的效果,本文假设只存在白噪声的情况下,利用最小二乘分别对经过滤波和同时经过滤波与小波变换后的时间序列去除线性趋势、周年半周年信号,获得残差时间序列的其标准差,具体结果见表 1。其中,Ⅰ列数据为原始时间序列经过区域叠加滤波后拟合残差的标准差;Ⅱ列数据为对时间序列进行区域叠加滤波以及小波变换后拟合残差的标准差。比较Ⅰ列与Ⅱ列数据可知,经过滤波以及小波处理后的时间序列所含噪声比滤波后的时间序列大幅度减小。其中水平方向减小幅度约为40%,垂直方向减小幅度超过50%。
| mm | ||||||||
| 测站 | North | East | Vertical | |||||
| Ⅰ | Ⅱ | Ⅰ | Ⅱ | Ⅰ | Ⅱ | |||
| AVRY | 48.78 | 25.88 | 43.08 | 18.05 | 165.67 | 60.21 | ||
| AZU1 | 59.25 | 38.11 | 50.41 | 32.14 | 249.03 | 122.83 | ||
| BBRY | 74.23 | 46.21 | 45.30 | 19.12 | 201.78 | 67.09 | ||
| BILL | 40.85 | 24.29 | 34.04 | 22.29 | 145.56 | 53.78 | ||
| BSRY | 46.32 | 23.40 | 43.11 | 24.15 | 160.00 | 62.75 | ||
| CLAR | 61.08 | 44.66 | 42.21 | 29.86 | 194.89 | 112.39 | ||
| CTDM | 46.82 | 21.67 | 42.73 | 21.92 | 182.92 | 92.77 | ||
| CTMS | 72.60 | 51.51 | 47.38 | 22.70 | 185.57 | 75.28 | ||
| EWPP | 51.87 | 25.24 | 44.17 | 20.38 | 198.86 | 89.38 | ||
| MAT2 | 39.60 | 21.69 | 35.64 | 22.61 | 146.43 | 64.36 | ||
| SDHL | 69.00 | 57.17 | 40.15 | 20.41 | 145.39 | 49.34 | ||
| SFDM | 56.65 | 29.86 | 45.59 | 25.02 | 215.21 | 107.22 | ||
| SPK1 | 49.63 | 25.46 | 46.98 | 24.04 | 176.37 | 92.64 | ||
| TABL | 64.29 | 32.97 | 62.17 | 36.86 | 206.77 | 95.71 | ||
| TORP | 74.30 | 62.67 | 46.38 | 29.43 | 184.83 | 105.07 | ||
| VNCX | 45.96 | 17.03 | 43.74 | 26.60 | 169.70 | 62.36 | ||
| 减小百分比均值 | 41% | 44% | 56% | |||||
本文首先利用区域叠加滤波法去除了南加利福尼亚地区16个测站坐标时间序列的共模误差,在此基础上通过静态离散小波变换去除频率大于2.85 cpy的误差。结果表明,通过区域叠加滤波法去除共模误差,可以削弱周期性误差尤其是周年与半周年误差对原始坐标时间序列周期信号的影响。对去除共模误差后的时间序列再进行静态离散小波变换,可以从滤波后的坐标时间序列中提取周期为半周年以上的长周期信号,进一步剔除剩余误差的影响,最终实现信噪的有效分离。这有助于提高GPS测站的位置精度及其非线性运动的地球物理因素的解释,对于高精度的地壳形变监测具有积极的意义。
| [1] | DONG D, FANG P, BOCK Y, et al. Anatomy of Apparent Seasonal Variations from GPS-derived Site Position Time Series[J]. Journal of Geophysical Research Atmospheres, 2002, 107(B4): 9–16. |
| [2] | STEWART M P, PENNA N T, LICHTI D D, et al. Investigating the Propagation Mechanism of Unmodelled Systematic Errors on Coordinate Time Series Estimated Using Least Squares[J]. Journal of Geodesy, 2005, 79(8): 479–489. DOI:10.1007/s00190-005-0478-6 |
| [3] | PENNA N T, KING M A, STEWART M P. GPS Height Time Series:Short-period Origins of Spurious Long-period Signals[J]. Journal of Geophysical Research, 2007, 112(B2): 1074–1086. |
| [4] | PENNA N T, STEWART M P. Aliased Tidal Signatures in Continuous GPS Height Time Series[J]. Geophysical Research Letters, 2003, 30(23): 69–73. |
| [5] | DONG D, FANG P, BOCK Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research Atmospheres, 2006, 111(B3): 1581–1600. |
| [6] | WDOWINSKI S, BOCK Y, ZHANG J, et al. Southern California Permanent GPS Geodetic Array:Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research Atmospheres, 1997, 1021(1021): 18057–18070. |
| [7] | NIKOLAIDIS R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[M].[S.l.]:American Association for Cancer Research, 2002. |
| [8] | JACKSON D A, CHEN Y. Robust Principal Component Analysis and Outlier Detection with Ecological Data[J]. Environmetrics, 2010, 15(2): 129–139. |
| [9] | 杨博, 周伟, 陈阜超, 等. GPS连续站水平位置时间序列共模白噪声识别与估计的欧拉-滤波法[J]. 山东科技大学学报(自然科学版), 2010, 29(3): 26–31. |
| [10] | 范玉磊, 王贺, 黄声享, 等. 利用小波分析IGS跟踪站的非线性运动特征[J]. 测绘工程, 2014, 23(9): 5–8. |
| [11] | 田亮, 孙付平. 基于GPS测站坐标残差序列的小波工具应用与分析[J]. 测绘工程, 2013, 22(1): 44–47. |
| [12] | 李尊建, 臧斌. 非平稳大地测量信号特征信息小波识别[J]. 山东理工大学学报(自然科学版), 2009, 23(4): 58–61. |
| [13] | MÁRQUEZ-AZÚA B, DEMETS C. Crustal Velocity Field of Mexico from Continuous GPS Measurements, 1993 to June 2001:Implications for the Neotectonics of Mexico[J]. Journal of Geophysical Research Atmospheres, 2003, 108(B9): 149–169. |
| [14] | 盛传贞. 中国大陆非构造负荷地壳形变的区域性特征与改正模型[D]. 北京: 中国地震局地质研究所, 2013. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gjzt201411004&dbname=CJFD&dbcode=CJFQ |
| [15] | 袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1372–1384. |
| [16] | 姜卫平, 李昭, 邓连生, 等. 高阶电离层延迟对GPS坐标时间序列的影响分析[J]. 科学通报, 2014, 59(10): 913–923. |
| [17] | 唐江森, 曲国庆, 袁兴明. 区域GPS网共模误差的提取与分析[J]. 山东理工大学学报(自然科学版), 2016, 30(6): 48–52. |
| [18] | 贺小星. GPS坐标序列噪声模型估计方法研究[D]. 武汉: 武汉大学, 2016. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=chxb201703017&dbname=CJFD&dbcode=CJFQ |
| [19] | WU H, LI K, SHI W, et al. A Wavelet-based Hybrid Approach to Remove the Flicker Noise and the White Noise from GPS Coordinate Time Series[J]. GPS Solutions, 2015, 19(4): 511–523. DOI:10.1007/s10291-014-0412-6 |


