2. 武汉大学遥感信息工程学院, 湖北 武汉 430079
2. School of Remote Sensing Information Engineering, Wuhan University, Wuhan 430079, China
快速、准确地重建物体的表面模型在逆向工程、工业制造、虚拟环境构建等诸多领域具有重要意义[1-3]。基于倾斜影像的曲面重建是曲面重建的方式之一,可以快速获取地表模型,在地形地貌分析、数字城市建设中得到了广泛的应用[4-6]。
基于倾斜影像的曲面重建流程可大致分为:①倾斜影像同名点提取;②空中三角测量;③影像密集匹配生成点云;④基于点云的曲面重建。根据曲面重建的表示方式,可将曲面重建方法分为显式曲面方法、隐式曲面方法[7]。文献[8-10]使用Voronoi图和Delaunay三角网来确定点与点之间的连接并最终通过连接相邻顶点来重建曲面,文献[11-13]采用参数曲面来表示曲面重建,这些方法均是显式曲面方法。使用显式曲面重建的一大优点是可以精确简洁地表示曲面情况[14],但是显式曲面方法难以处理点云中的噪声和孔洞问题,主要是由该方法的自身特性所决定的:①所有的点都被作为三角网的顶点;②点与点是通过最邻近信息来确定连接关系的,缺乏全局性。除此之外,由于缺乏体积信息,显式曲面重建方法在处理复杂的拓扑结构时不够稳定和灵活[14]。
隐式曲面重建方法是通过隐函数拟合数据点,然后在零值面上提取三维网格曲面[7],文献[15]使用分段二次函数表示模型局部表面形态,文献[16]使用平滑符号距离函数来重建水密性的模型表面等均属于隐式曲面重建。隐式曲面重建方法中使用的隐函数典型的有B样条函数、径向基函数和多项式函数,而提取三角网格的方法以Marching Cubes[17]多边形化为主。本文所提出的重建方法中涉及的隐式曲面重建即是以B样条函数为隐函数的Screened Poisson曲面重建[18]。隐式曲面重建方法对含噪声数据有更强的适应性,然而在点云稀疏区域,仅仅以点云的坐标数据,隐式曲面重建方法往往难以准确地反映目标的真实表面模型,以Screened Poisson曲面重建为例,在此情形下,目标点云稀疏区域的重建形态是B样条曲面形态的反映,而非目标区域的形态。
而在基于倾斜影像的城市场景曲面重建中,由于获取影像时存在遮蔽和大视点变化的原因,建筑物立面等易遮蔽区域的影像重叠度不高,导致后期此类区域密集匹配点云稀疏甚至出现空洞,曲面重建难度大。目前,文献[19]提出一种针对大规模场景的表面重建方法,对密集匹配点云进行空间四面体剖分,对四面体进行图割提取出表面模型,然后利用影像对生成模型进行了变分优化处理,该方法较好地保留了建筑物的原始细节形态。
本文针对城市区域倾斜影像的特点提出了一种新的城市场景重建算法。由于众多隐式曲面重建方法在重建过程中会使用点云的法向信息,通过拟合平面[20-21]等方法在点云稀疏区域难以获取准确法向量信息。因此,本文方法在倾斜摄影隐式曲面重建中利用不局限于点云坐标的信息来修正点云的法向信息:首先,以影像密集匹配点云为基础建立Delaunay四面体;然后,对Delaunay四面体进行基于光线的可视性约束图割,进而更加精确地估计点云的法向信息;最后,结合Screened Poisson曲面重建,实现城市场景隐式表面重建。
1 方法本文提出的基于倾斜影像的城市场景隐式曲面重建流程可大致分为:影像特征点提取、空中三角测量、影像密集匹配生成点云、构建Delaunay四面体并进行约束图割、点云法向信息计算和Screened Poisson表面重建6个步骤。本文关注由密集匹配点云到曲面生成这一三维构网过程。
通常,基于三维激光点云进行隐式曲面重建时,由于点云密集,并且缺乏更多的信息(如光线信息)来修正点云的法向信息,在计算点云的法向量时采用以下步骤:①利用最邻近算法取目标点周围一定范围内或一定数量的点;②对这些点进行拟合,拟合出一个平面;③计算目标点的法向量。然而,由于倾斜影像密集匹配点云自身的特点:点云分布不均,城市中建筑立面等区域密集匹配点云稀疏,利用上述常规的点云法向计算方法误差较大。
本文提出的方法较好地解决了上述问题,有效利用了点云的光线信息。首先基于密集匹配点云(包含相机位置)建立Delaunay四面体,并建立特殊的s-t图,根据四面体的光线可视性等信息对四面体进行标记[22],利用最小割算法[23]最优化标记结果,最终提取出城市场景的三角面,以Delaunay三角网的形式很好地保留了点云稀疏区域的形态特征,可以更加准确地计算出点云的法向量信息。图 1为本文算法的流程。
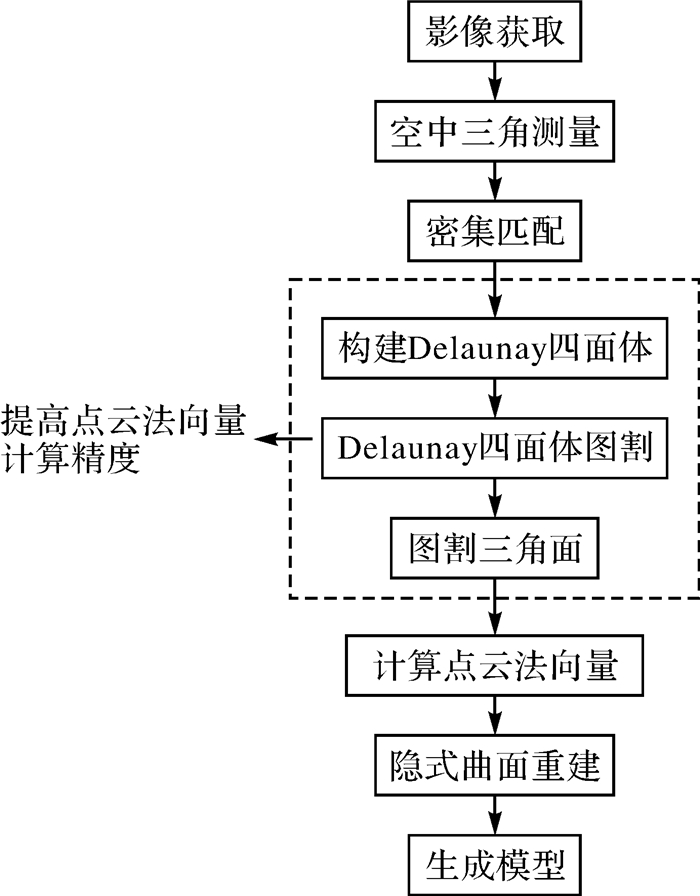
|
| 图 1 基于倾斜影像的城市场景隐式曲面重建流程 |
利用基于Delaunay四面体的约束图割方法建立起城市场景的可视化三角面,首先要将Delaunay四面体标记为场景的外部或内部,然后从相邻的不同标记结果的四面体中提取出所需的三角网。
本文使用最小割算法对全局标记结果进行优化,为此,建立三维空间中的s-t图[24],如图 2所示。图 2中,与光线相交的三角形在s-t图中相应有向边增加权值。δ是偏移距离,用来确定与汇(t)相连的Delaunay四面体。最后一个与光线相交的四面体或包含相机中心的四面体与源(s)相连。Delaunay四面体的对偶——Voronoi多面体中的有向边和节点对应s-t图中的有向边和节点。图 2中(二维平面内),三角形表示Delaunay四面体,浅灰色Voronoi多边形区域表示Delaunay四面体的对偶图——Voronoi多面体。
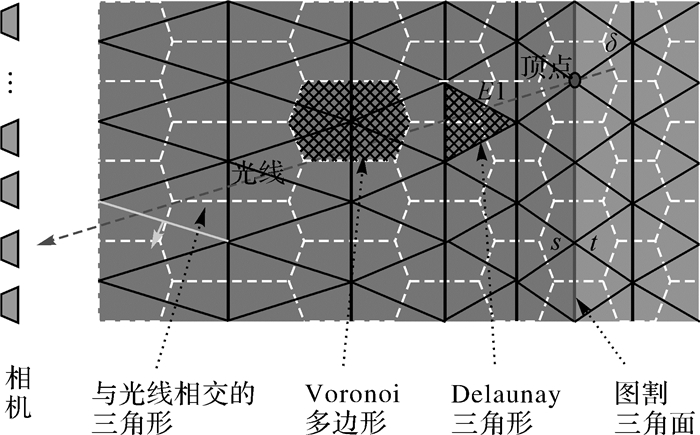
|
| 图 2 基于Delaunay四面体中的s-t图平面示意图 |
以S表示基于四面体的约束图割输出的三角面,S是带有方向的Delaunay三角形的组合。定义与S相关的能量E(S)
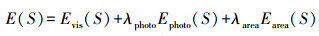 (1)
(1) 式中,λphoto和λarea是正权值。最小化能量E(S)即可以实现Delaunay四面体标记结果的最优化,并得到所需的输出表面。接下来将介绍每个能量项在s-t图中的定义,并分析最小化能量E(S)为何能对Delaunay四面体实现最优化标记。
1.1.1 曲面可视性基于倾斜影像的密集匹配点云里每个点(物方点)都至少能在两张影像上找到对应的影像坐标(像方点)。这一信息与能量项Evis(S)相关:Delaunay四面体中的每个顶点对应的影像中的视点分别与该顶点连接成光线并向前延伸一定的长度,这条光线穿过四面体,如果四面体在这个顶点与视点中间,则被标记为外部,相反,如果四面体在这个顶点之后,则标记为内部,根据该光线的标记结果,为s-t图中相应的有向边赋予权值λout(外部)或者λin(内部)。
图 2中,E1为与光线相交的Delaunay三角形的对应的Voronoi多边形的3条有向边之一,该三角形被标记为外部,则
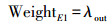 (2)
(2) δ所在位置的三角形对应的Voronoi多边形有向边的权值t-weight为λin,最后与光线相交或包含相机位置的四面体在s-t图中对应的有向边被赋予无穷大的权重s-weight。
对四面体中的所有节点重复以上操作,如果s-t图中的有向边已经被赋予权重,就把新赋的权重累加到之前已经存在的权重上。
曲面可视性能量项Evis(S)综合了s-t图里所有权重边的信息,利用可视性能量项对每个四面体的标记情况进行全局性“投票”,通过这种全局优化的过程,可以使该方法抵抗多种类的噪声及误差。
1.1.2 曲面影像一致性影像一致性能量项Ephoto(S)表征了曲面和倾斜影像的匹配度,定义如下
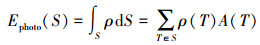 (3)
(3) 式中,ρ是曲面中包含的任意一个三角形的影像一致性量度。
任意三角形的影像一致性量度是通过该三角形包含的3个顶点在影像中的匹配信息计算出的。由于曲面S里包含的每个三角形是从相邻的不同标记的四面体中提取出的,因此,曲面的影像一致性能量项要考虑三角形的方向。这里将曲面影像一致性能量项融入特殊图里的图割框架中:对任意拥有公共三角面的两个Delaunay四面体(用特殊图里的节点p和q表示),特殊图中的边p→q被赋予权重
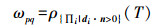 (4)
(4) 式中,di表示了从三角形的中心到第i张影像的相机中心∏i的方向。
1.1.3 曲面平滑度曲面平滑度能量项Earea(S)被用来最小化曲面的面积,定义如下
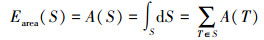 (5)
(5) 对任意拥有公共三角面的两个Delaunay四面体(用特殊图里的节点p和q表示),特殊图中的边p→q被赋予权重ωpq=A(T),并且,相反方向的边q→p被赋予相同的权重ωqp=ωpq。
利用最小割算法找到s-t图的最小割,对应于能量E(S)的最小化,实现四面体的全局最优化标记。
1.2 点云法向量信息计算对Delaunay四面体进行基于光线的可视性约束图割后,生成一个城市场景的显式曲面,本节基于此曲面计算倾斜影像密集匹配点云的法向信息。
点p为三角面s1、s2、…、sm的公共顶点,三角面的法向量为:n1、n2、…、nm。设
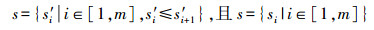 (6)
(6) s对应的法向为
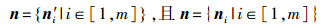 (7)
(7) 则点p的法向量可以表示为
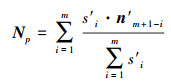 (8)
(8) 本文提出的基于倾斜影像的城市场景隐式曲面重建方法是以Kazhdan等提出的隐式曲面重建方法——Screened Poisson曲面重建[18]为例来完成最终的曲面重建。Screened Poisson曲面重建能够从有向点云中重建出水密性的曲面。
1.3.1 示性函数拟合Poisson曲面重建方法[25]是基于实体模型表面的法向量和实体模型的示性函数的梯度相等这一原理展开的,基于有向点云数据集可以生成一个水密的表面,但是该算法对示性函数进行修正时使用的是全局性的偏移,使得在所有点的函数值的平均值为0,然而由于误差的存在使得示性函数难以找到一个合适的全局偏移值,Kazhdan等最终提出了Screened Poisson曲面重建,在示性函数求解时,引入点集位置约束。模型的示性函数用χ表示,χ=0表示模型的表面。
给定向量场V:R3→R3,目的是为了求解示性函数χ:R3→R的最小值
 (9)
(9) 式中,∇χ(p)为模型表面某点处的梯度;V(p)为实体模型表面的法向量函数;α为Screened参数项,用来平衡梯度拟合值与模型示性函数值;w(p)为给每个点赋予的权重;Area(S)为重建区域的面积,该区域是根据采样密度的计算来估计的。
V(p)定义如下
 (10)
(10) 式中,s为输入数据集的一个样本,包含点坐标s.p和该点法向量s.N;NgbrD(s)为与s.p最邻近的8个深度为D的节点;αo, s为三线性插值权重;Fo(p)为基函数。
式(9)可以简化为
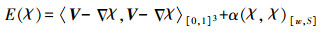 (11)
(11) 式中,〈., .〉[w, S]表示在单位立方体体素中的函数空间的形式,具备双线性、对称性、非负性及半正定性,该值是根据函数值的加权和得到的
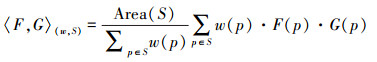 (12)
(12) 式(11)将梯度约束和点云的误差约束整合进空间域,利用Euler-Lagrange方程,通过求解Poisson方程可以得到χ的最小解
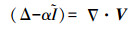 (13)
(13) 同Poisson曲面重建一样,这里对Screened Poisson曲面重建需要对泊松方程进行离散化处理。示性函数χ关于一组基{B1, B2, …, Bn}的系数可以通过求解线性系统Ax=b得到。其中
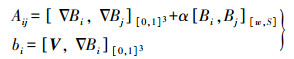 (14)
(14) Screened Poisson曲面重建算法引入瀑布型多重网格法对线性系统进行求解,随着八叉树的深度发生变化(从浅到深),系统求解从粗糙到精细。求解深度在d′层而约束在d层的矩阵可表示如下
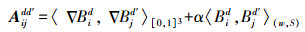 (15)
(15) 求解Screened Poisson方程可以得到示性函数的近似解χ,理想情况下,示性函数的零水平集对应着所需的曲面,然而由于存在误差,需要选择合适的全局偏移值来修正指示函数χ,然后利用Marching-Cubes方法从函数χ中提取出等值面。
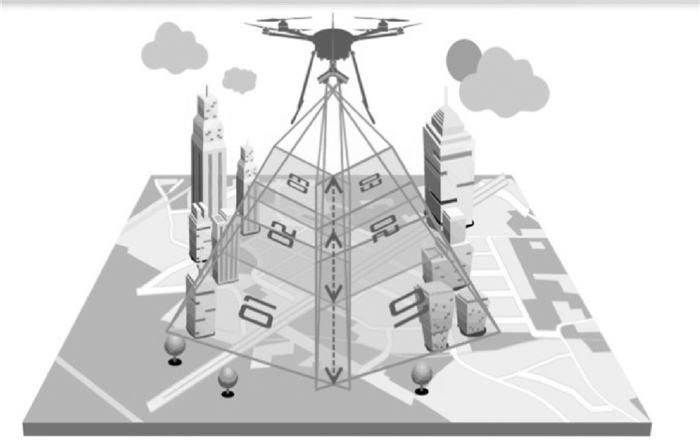
2 试验及分析 2.1 数据描述本文中使用的倾斜影像是利用无人机在山西某城市以离地150 m的高度倾斜摄影得到的。利用两台相机同时前后摆动,每次摆动角度为60°,一个周期内可以拍摄6张影像,每张影像的像元数为4000× 6000,空间分辨率为3~10 cm。图 3显示了倾斜摄影测量系统获取影像的过程,图 4是利用该系统在一个周期内获取的6张倾斜影像。
|
| 图 3 无人机倾斜摄影示意图 |

|
| 图 4 倾斜影像 |
试验中利用半全局匹配算法(SGM)[26]对倾斜影像进行了密集匹配,然后基于计算几何算法库(CGAL)[27]建立了Delaunay四面体。在前文中,笔者对Delaunay四面体进行基于光线约束的最小化图割。
在试验中,笔者将本文方法的城市场景曲面重建精度与Screened Poisson曲面重建[18]、Poisson曲面重建[25]、小波流曲面重建[28]、平滑符号距离重建[16]4种曲面重建精度作比较。笔者将曲面重建中涉及的八叉树深度(octree depth)统一设置为10。对于Screened Poisson曲面重建算法,笔者将点的权重(pointWeights)设置为4;在小波流曲面重建(Wavelet)中,使用Haar小波来完成曲面重建。
2.3 试验结果以Screened Poisson曲面重建、Poisson曲面重建、基于Haar小波的流曲面重建(Haar Wavelet)和平滑符号距离曲面重建(SSD)4种隐式曲面重建方法为例,分别将这4种曲面重建方法作为本文算法中的曲面重建方法,完成曲面重建工作,并对应地与这4种算法在相同三维点云数据集(不包含光线信息)下的重建精度作定性与定量比较。如图 5、图 6所示。

|
| 图 5 倾斜影像密集匹配点云 |

|
| 图 6 本文算法重建效果(结合Screened Poisson重建) |
图 7显示了本文提出的基于倾斜影像的城市场景隐式曲面重建算法与经典算法的城市场景重建结果,并选取了典型的建筑立面区域(如图 8所示),比较了重建结果的精度。以图 7(a)为例,左图 1为本文方法(结合Screened Poisson曲面重建)的城市场景曲面重建结果,左图 2是从左图 1中拾取的精度对比目标区域;右图 1为Screened Poisson曲面重建在相同点云数据集(不使用光线信息)下的重建结果,右图 2是从右图 1中拾取的精度对比目标区域(与左图 2对应同一建筑立面区域)的重建效果。参考目标区域对应的原始倾斜影像(如图 8所示),可发现在4组对比试验中,基于本文方法的重建效果优于对应的经典重建方法的重建效果,尤其是在建筑立面区域,本文算法很好地保留了建筑的原始特征。

|
| 图 7 基于倾斜影像的城市场景隐式曲面重建与经典算法重建结果 |

|
| 图 8 城市建筑区域倾斜影像 |
为了进一步定量检验本文算法的有效性,笔者使用Metro[29]程序分别对图 7表示的4组曲面重建结果作比较,表 1列出了城市场景曲面重建的曲面精度等信息。
| 组号 | 重建算法 | 三角面数 | 平均距离 | RMS | Hausdroff距离 (相对于包围盒对角线) |
| 1 | 本文方法 | 2 004 924 | 0.191 222 | 0.594 911 | 0.009 288 |
| Screened Poisson | 2 263 398 | ||||
| 2 | 本文方法 | 1 891 708 | 0.872 204 | 1.839 314 | 0.011 731 |
| Poisson | 1 959 411 | ||||
| 3 | 本文方法 | 1 652 116 | 0.864 803 | 1.697 392 | 0.007 391 |
| 平滑符号距离(SSD) | 1 676 132 | ||||
| 4 | 本文方法 | 1 659 664 | 0.398 123 | 1.998 851 | 0.074 903 |
| Harr小波 | 1 701 240 |
联合上述定性与定量的试验分析,可以得出结论:本文提出的基于倾斜影像的城市场景隐式曲面重建算法能够以很高的精度重建城市场景,尤其在建筑立面等区域,较好地保留了原有的形态。
3 结语本文提出了一种新的城市场景三维重建方法:首先基于密集匹配点云集对空间进行三维Delaunay三角剖分;然后,建立空间中的s-t图,利用最小割算法,对Delaunay四面体进行优化标记,并提取出粗糙的三角面,利用三角面的拓扑关系,进而更加精确地估计点云的法向信息;最终结合隐式曲面重建方法(Screened Poisson曲面重建)对城市三维场景进行重建。试验表明该方法很好地重建了城市的三维场景,尤其是在城市的建筑立面等区域,比几种经典的算法都取得了更优的重建结果。然而在点云稀疏、形态较为复杂的区域,如窗台等,隐式曲面重建方法难以较为规则地重建出目标原始形态,后续研究需要解决城市场景的细节区域的自动化、规则化重建。
| [1] | GAO J, CHEN X, YILMAZ O, et al. An Integrated Adaptive Repair Solution for Complex Aerospace Components through Geometry Reconstruction[J]. The International Journal of Advanced Manufacturing Technology, 2008, 36(11-12): 1170–1179. DOI:10.1007/s00170-006-0923-6 |
| [2] | YANG M D, CHAO C F, HUANG K S, et al. Image-Based 3D Scene Reconstruction and Exploration in Augmented Reality[J]. Automation in Construction, 2013(33): 48–60. |
| [3] | WANG J, GU D, YU Z, et al. A Framework for 3D Model Reconstruction in Reverse Engineering[J]. Computers & Industrial Engineering, 2012, 63(4): 1189–1200. |
| [4] | JAMES M, ROBSON S. Straightforward Reconstruction of 3D Surfaces and Topography with a Camera:Accuracy and Geoscience Application[J]. Journal of Geophysical Research:Earth Surface, 2012, 117(F3). DOI:10.1029/2011JF002289 |
| [5] | 史文中, 曹辉, 张剑清. 基于高分辨率影像的城市三维建模[J]. 武汉大学学报(信息科学版), 2004, 29(9): 783–787. |
| [6] | 朱庆, 徐冠宇, 杜志强, 等. 倾斜摄影测量技术综述[J]. 北京:中国科技论文在线, 2012. |
| [7] | LIM S P, HARON H. Surface Reconstruction Techniques:A Review[J]. Artificial Intelligence Review, 2014, 42(1): 59–78. DOI:10.1007/s10462-012-9329-z |
| [8] | AMENTA N, BERN M, KAMVYSSELIS M.A New Voronoi-based Surface Reconstruction Algorithm[C]//Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques.New York:ACM, 1998:415-421. |
| [9] | EDELSBRUNNER H. Shape Reconstruction with Delaunay Complex[J]. Lecture Notes in Computer Science, 1980, 1380(1380): 119–132. |
| [10] | AMENTA N, BERN M, EPPSTEIN D. The Crust and the β-Skeleton:Combinatorial Curve Reconstruction[J]. Graphical Models and Image Processing, 1998, 60(2): 125–135. DOI:10.1006/gmip.1998.0465 |
| [11] | DECARLO D, DIMITRI. Blended Deformable Models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(4): 443–448. DOI:10.1109/34.491626 |
| [12] | HE Y, QIN H.Surface Reconstruction with Triangular B-splines[C]//Geometric Modeling and Processing.Beijing:[s.n.], 2004:279-287. |
| [13] | MARR D, NISHIHARA H K. Representation and Recognition of the Spatial Organization of Three-dimensional Shapes[J]. Proceedings of the Royal Society of London, 1978, 200(1140): 269–294. DOI:10.1098/rspb.1978.0020 |
| [14] | LIANG J, PARK F, ZHAO H. Robust and Efficient Implicit Surface Reconstruction for Point Clouds Based on Convexified Image Segmentation[J]. Journal of Scientific Computing, 2013, 54(2-3): 577–602. DOI:10.1007/s10915-012-9674-8 |
| [15] | OHTAKE Y, BELYAEV A, ALEXA M, et al. Multi-level Partition of Unity Implicits[J]. ACM Siggraph, 2003, 22(3): 463–470. DOI:10.1145/882262 |
| [16] | CALAKLI F, TAUBIN G. SSD:Smooth Signed Distance Surface Reconstruction[J]. Computer Graphics Forum, 2011, 30(7): 1993–2002. DOI:10.1111/cgf.2011.30.issue-7 |
| [17] | LORENSEN W E, CLINE H E. Marching Cubes:A High Resolution 3D Surface Construction Algorithm[J]. ACM Siggraph Computer Graphics, 1987, 21(4): 163–169. DOI:10.1145/37402 |
| [18] | KAZHDAN M, HOPPE H. Screened Poisson Surface Reconstruction[J]. ACM Transactions on Graphics (TOG), 2013, 32(3): 1–13. |
| [19] | HIEP V H, KERIVEN R, LABATUT P, et al.Towards High-resolution Large-scale Multi-view Stereo[C]//IEEE Conference on Computer Vision and Pattern Recognition.[S.l.]:IEEE, 2009:1430-1437. |
| [20] | MITRA N J, NGUYEN A.Estimating Surface Normals in Noisy Point Cloud Data[C]//Proceedings of the 19th Annual Symposium on Computational Geometry.[S.l.]:ACM, 2003:322-328. |
| [21] | HOPPE H, DEROSE T, DUCHAMP T, et al.Surface Reconstruction from Unorganized Points[C]//Proceedings of ACM Siggraph.[S.l.]:ACM, 1992. |
| [22] | LABATUT P, PONS J-P, KERIVEN R.Efficient Multi-view Reconstruction of Large-scale Scenes Using Interest Points, Delaunay Triangulation and Graph Cuts[C]//IEEE 11th International Conference on Computer Vision.[S.l.]:IEEE, 2007:1-8. |
| [23] | BOYKOV Y, KOLMOGOROV V. An Experimental Comparison of Min-cut/max-flow Algorithms for Energy Minimization in Vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(9): 1124–1137. DOI:10.1109/TPAMI.2004.60 |
| [24] | BOYKOV Y Y, JOLLY M P.Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in ND Images[C]//Proceedings of Eighth IEEE International Conference on Computer Vision.Vancouver:IEEE, 2001:105-112. |
| [25] | KAZHDAN M, BOLITHO M, HOPPE H.Poisson Surface Reconstruction[C]//Proceedings of the 4th Eurographics Symposium on Geometry Processing.[S.l.]:[s.n.], 2006:61-70. |
| [26] | HIRSCHM LLER H. Stereo Processing by Semiglobal Matching and Mutual Information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(2): 328–341. DOI:10.1109/TPAMI.2007.1166 |
| [27] | BOISSONNAT J D, DEVILLERS O, TEILLAUD M, et al.Triangulations in CGAL[C]//Proceedings of the 16th Annual Symposium on Computational Geometry.[S.l.]:ACM, 2000:11-18. |
| [28] | MANSON J, PETROVA G, SCHAEFER S.Streaming Surface Reconstruction Using Wavelets[C]//Computer Graphics Forum.[S.l.]:[s.n.], 2008:1411-1420. |
| [29] | CIGNONI P, ROCCHINI C, SCOPIGNO R.Metro:Measuring Error on Simplified Surfaces[C]//Computer Graphics Forum.[S.l.]:[s.n.], 1998:167-174. |


