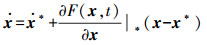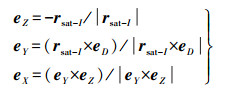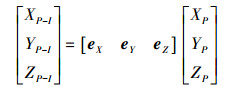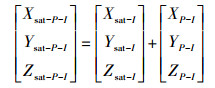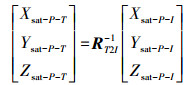2. 中国测绘科学研究院, 北京 100830;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉 430079
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. GNSS Research Center, Wuhan University, Wuhan 430079, China
随着用户导航定位、地震海啸灾害预警、空间天气探测等科学研究及应用领域的不断发展,实时位置服务已经成为GNSS应用的发展趋势,而实时轨道的确定和播发是GNSS实时位置服务的核心技术。中国北斗卫星导航系统(BDS)是我国自行研制、独立运行的全球卫星定位与通信系统,其空间部分采用地球静止轨道(geostationary earth orbit,GEO)、倾斜地球同步轨道(inclined geosynchronous satellite orbit,IGSO)及中地球轨道(medium earth orbit,MEO)混合星座设计[1-2]。2012年10月,第16颗北斗卫星成功发射,标志着我国北斗导航工程区域组网顺利完成,2020年前后,我国共将发射约40颗北斗导航卫星,完成覆盖全球的系统建设目标。目前,BDS广播星历IGSO和MEO卫星精度优于2 m,GEO卫星精度较低[3],难以满足实时定位需求。随着北斗系统空间段与地面段建设的日趋完善,我国开始筹建BDS广域增强系统,生成高精度的实时轨道、钟差、电离层等产品信息,以满足实时用户应用。
近年来,由于用户对实时产品的迫切需求,国内外众多研究和商业机构陆续提供实时服务,2002年IGS成立了实时工作组(Real-time Working Group),进行实时产品的研究[4];2007年,IGS开始运行IGS-RTPPP项目,实时估计卫星轨道和钟差;2011年,SSR(state space represention)信息格式正式成为RTCM推荐的开放格式之一,多个国际IGS分析中心(BKG、JPL、GFZ、WHU等)采用SSR信息格式播发包含实时轨道、钟差改正的NTRIP数据流[5]。2015年千寻位置网络有限公司成立,以“互联网+位置(北斗)”的理念,基于云计算和数据技术,构建位置服务云平台,以满足国家、行业、大众市场对位置服务的需求。Furgo公司于2009年开始启动全球精密定位服务,采用全球分布测站,进行实时轨道和钟差的解算,通过GEO卫星播发实时增强信息改正数[6];Trimble公司从2011年9月开始在全球范围内提供实时GNSS定位服务,支持GPS/GLONASS/QZSS系统,其水平精度可以达到厘米级[7]。文献[5,8-10]进行GPS实时轨道和钟差确定的测试,并开发相应的系统,开展了广域实时精密定位原型系统的研究。但BDS实时轨道的确定尚处于发展阶段,其存在异构星座、轨道周期不尽相同、全球跟踪站数量少、分布不均匀等现实因素。目前RTCM3.X协议中的SSR改正并未包含北斗信息模块,其IODE(issue of data,ephemeris)值并不适合BDS改正信息的播发,因此其SSR改正信息生成和编码有待研究。国家测绘地理信息局组织实施的国家现代测绘基准体系基础设施建设项目,在全国均匀布设了360个国家GNSS连续运行基准站(简称国家基准站)[11],其中210个站具备接收四系统卫星数据的能力,可为北斗实时轨道确定及服务提供数据资源。本文讨论北斗卫星实时轨道的解算策略,并给出SSR信息中基于卫星质心和相位中心的实时轨道改正数的生成方法,根据SSR格式,自定义一种适合BDS改正数播发的IODE值的表达,基于国家基准站和全球MGEX(multi-GNSS experiment)测站进行BDS卫星实时定轨测试,并与iGMAS (international GNSS monitoring & assessment system)最终轨道产品结果进行比对。
1 卫星精密定轨原理导航卫星GNSS精密定轨中,状态向量x包含卫星轨道参数(位置、速度)、力模型参数(光压模型等物理参数)及其他待估参数(钟差、相位模糊度等)等。对于动力学模型,满足如下方程
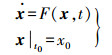 (1)
(1) 式中,x0为初始状态;F为n维非线性函数,将式(1)线性化为[12]
式中,x*为基于某时刻的参考轨道初值。令X = x -x*,A =∂F(x,t)/∂x,可得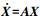
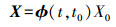 (2)
(2) 式中,ϕ(t,t0)为状态转移矩阵,可根据数值积分求得。同时,地面站GNSS观测为定轨提供了几何信息。设地面跟踪站的观测量为Y,第i历元的观测数据yi与其真值G(xi,ti)和测量误差εi的观测方程为[13]
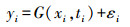 (3)
(3) 因此将式(3)非线性方程展开后,结合式(2)可得
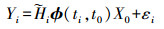 (4)
(4) 式中,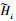
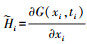
对于高度20 000多千米的MEO卫星、30 000多千米的GEO和IGSO卫星,在非机动和故障情况下,卫星轨道的变化是平滑稳定的,因此短时间的预报轨道可以达到很高的精度。由于其MEO卫星运行周期为12 h 53 min,GEO和IGSO卫星运行周期为23 h 56 min[14],其异构星座的运行周期不同,加之GEO卫星定轨精度较低,造成单天解的预报轨道精度难以保证,因此本文采用短期预报模式,基于72 h的观测弧段进行BDS实时轨道的确定,即采用每次处理之前69 h的观测弧段,合并最新的3 h观测弧段为72 h观测弧段,利用一步法的最小二乘批处理进行轨道解算[15],并预报3 h弧段作为实时轨道产品,依次滑动。
3 卫星天线相位中心转换及其轨道改正信息生成SSR实时轨道改正信息中包含相对于广播星历的卫星位置改正值及速度改正值,用户接收到NTRIP播发的实时改正后,结合对应时刻的广播星历轨道参数,可以反算得到高精度的实时轨道,进行实时定位。其播发的改正值的参考点一般有两种:天线相位中心(antenna phase center,APC)和卫星质心(center of mass,COM)。本文根据SSR改正信息,在其格式统一的情况下,给出了分别基于卫星质心和相位中心的BDS的实时轨道改正计算方法,并定义了一种适合BDS广播星历IODE的匹配方式,SSR改正信息生成流程如图 1所示。
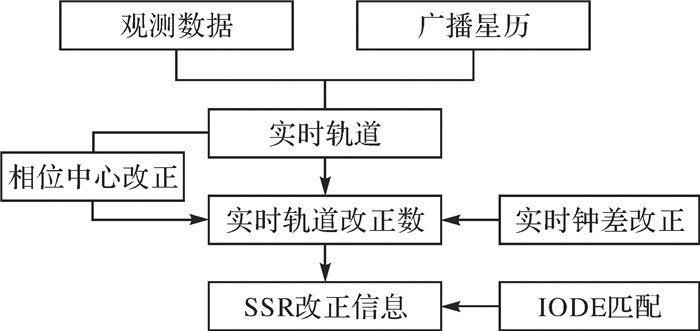
|
| 图 1 BDS SSR改正信息生成流程 |
卫星天线相位中心偏差的3个分量处于星固坐标系中[16],播发的轨道改正数处于轨道坐标系,需要进行星固坐标系、地心地固坐标系(简称地固系)、地心惯性系(简称惯性系)、轨道坐标系之间的转换,将天线相位中心改正到卫星质心位置中。
根据第1节,实时轨道确定得到北斗导航卫星在地固系中的质心坐标,通过以下公式得到卫星在惯性系中的坐标[12]
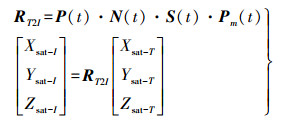 (5)
(5) 式中,(Xsat-I,Ysat-I,Zsat-I)为卫星在历元J2000.0对应的惯性系中的坐标;(Xsat-T,Ysat-T,Zsat-T)为卫星在地固坐标系中的坐标;P(t)、N(t)、S(t)、Pm(t)分别为t时刻的岁差矩阵、章动矩阵、地球自转矩阵、极移矩阵,可以从IERS2010协议中得到详细计算公式。
星固坐标系坐标轴在地心惯性系中的单位矢量可表示为
式中,rsat-I为卫星相对于地球质心的惯性矢量(由上式可以计算出); rsun-I为太阳相对于地球质心的惯性矢量(由行星表文件计算出)。则太阳至卫星方向单位矢量可表示为eD=(rsat-I-rsun-I)/|rsat-I-rsun-I|,卫星天线相位中心偏差在惯性系中为
式中,(XP,YP,ZP)为星固系中天线相位中心改正值;(XP-I,YP-I,ZP-I)为惯性系中天线相位中心改正值。经过天线相位中心改正后的惯性系中的卫星位置可以表示为
式中,(Xsat-P-I,Ysat-P-I,Zsat-P-I)为天线相位中心改正后的惯性系中的卫星位置,改正后的地固系中的卫星位置可以表示为
根据上式,地固系卫星实时轨道改正值可表示为
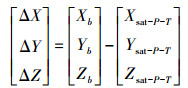 (6)
(6) 式中,(Xsat-P-I,Ysat-P-I,Zsat-P-I)为天线相位中心改正后的惯性系中的卫星位置;(ΔX,ΔY,ΔZ)为地固系中基于相位中心的卫星位置改正值;(Xb,Yb,Zb)为导航星历中卫星位置。采用地固系中卫星质心位置参与式(6)解算,得到地固系中基于质心的卫星位置改正值。因此
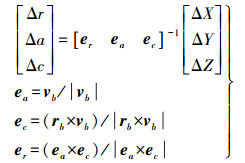 (7)
(7) 式中,(Δr,Δa,Δc)为轨道坐标系中卫星轨道改正值,分别为卫星径向、切向和法向方向;vb为地固系中卫星速度向量;rb为地固系中卫星位置向量。采用拉格朗日内插速度,可以得到卫星速度改正Δvr、Δva、Δvc。
GPS广播星历中IODE[16]代表数据龄期,对单颗卫星来说,不同历元的轨道参数对应的IODE是唯一的,因此实时用户根据SSR信息中IODE来选择相应的卫星轨道参数。而IODE在BDS和GPS广播星历定义中有差别,对BDS而言,难以作为唯一的匹配标准,因此考虑到BDS导航星历的历元间隔、不同历元的唯一性、字符长度等因素,根据SSR协议格式,自定义适合BDS的IODE,编码到SSR改正信息中,播发供用户使用,其计算方法为
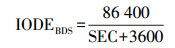 (8)
(8) 式中,IODEBDS∈[1,24]。
4 BDS卫星实时轨道精度分析本文采用全球20个均匀分布的国家基准站和60个MGEX站2017年001d—010d共10 d的观测数据,进行004d—010d的BDS实时轨道确定及SSR改正值播发,将实时预报的3 h轨道与iGMAS最终BDS轨道产品作对比[17],轨道实时解算策略见表 1。
| 类别 | 处理方法 | 类别 | 处理方法 |
| 观测值 | LC+PC无电离层组合观测值 | 参考钟 | 固定一个接收机钟 |
| 先验约束 | 伪距:1 m,载波:0.01周 | 测站坐标 | SNX文件+PPP结果 |
| 截止高度角 | 7° | 对流层 | Saastmoine模型+过程噪声 |
| 观测值加权 | p=1,e > 30°;p=4 sin2e,e≤30° | 卫星钟差 | 预报钟差+过程噪声 |
| 天线相位缠绕 | 模型改正 | 接收机钟差 | 伪距估计+白噪声 |
| 相位中心变化 | iGMAS推荐值 | 模糊度 | GEO卫星不固定IGSO/MEO卫星固定 |
图 2和图 3给出了每3 h为一个时段,连续7 d(共56个时段)的BDS实时轨道与iGMAS最终轨道比较统计得到的1D RMS值的时间序列,可以看出,GEO卫星轨道精度在100~400 cm,统计表明,90%以上的1D RMS值小于300 cm;IGSO和MEO卫星精度在30 cm以内。
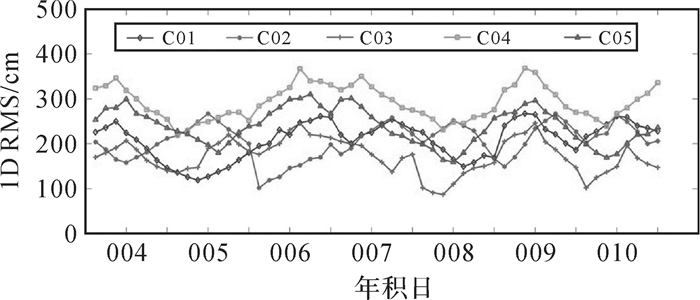
|
| 图 2 GEO卫星与最终轨道产品精度对比时间序列 |
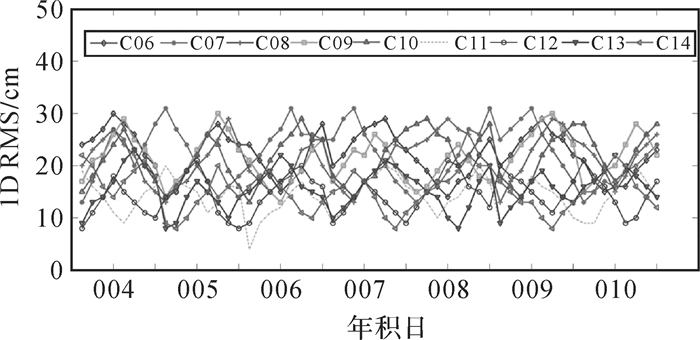
|
| 图 3 IGSO/MEO卫星与最终轨道产品精度对比时间序列 |
表 2统计了BDS实时轨道7 d的1D RMS平均精度,GEO卫星平均精度为223 cm,IGSO卫星为22 cm,MEO卫星为15 cm。而对于定位,卫星径向精度是主要影响因素,由图 4可知,GEO卫星轨道精度低主要体现在卫星切线方向,由于GEO卫星的静地和高轨特性[18],造成定轨的几何构型差。GEO卫星实时轨道径向精度优于20 cm,IGSO和MEO卫星径向精度优于10 cm,基本能够满足实时用户需求。
| cm | ||||||||||||||
| 卫星号 | C01 | C02 | C03 | C04 | C05 | C06 | C07 | C08 | C09 | C10 | C11 | C12 | C13 | C14 |
| 平均精度 | 208 | 206 | 172 | 292 | 239 | 22 | 22 | 21 | 21 | 22 | 14 | 15 | 16 | 15 |
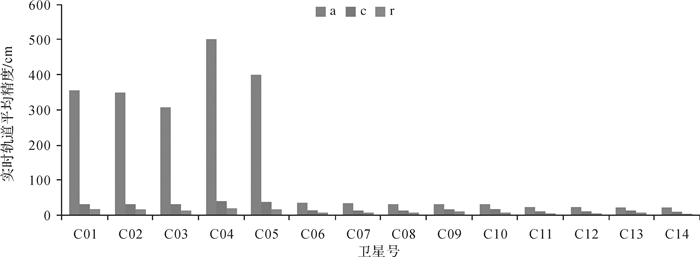
|
| 图 4 BDS实时轨道切向、法向和径向平均精度统计 |
随着北斗系统空间段与地面段建设的日趋完善,地面跟踪站数量和分布日趋合理,BDS的实时服务应用也会如火如荼地开展,本文根据卫星精密定轨的基本原理,在BDS实时轨道确定方法,轨道实时改正信息生成等方面进行了相关的研究,并基于国家基准站和MGEX站数据进行了测试,其主要结论如下:
(1) 针对北斗导航卫星星座的异构特性、轨道周期不同、测站分布不均匀等因素,基于轨道的短期预报,讨论了BDS 3 d解实时轨道滑动确定策略。
(2) 基于RTCM3.X的SSR信息格式,研究了基于北斗卫星质心和天线相位中心的SSR轨道改正值生成方法;针对BDS广播星历的历元间隔、播发字符长度等,给出了一种适合BDS的IODE值表达方式。
(3) 基于20个均匀分布的国家基准站及60个MGEX站,进行了BDS实时定轨测试,GEO卫星1D RMS精度优于400 cm,其径向精度优于20 cm;IGSO卫星精度优于30 cm,其径向精度优于10 cm;MEO卫星精度优于30 cm,其径向精度优于10 cm,基本满足实时用户的应用,为BDS实时位置服务提供了参考。
| [1] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. |
| [2] | SHI C, ZHAO Q L, LI M, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science China(Earth Sciences), 2012, 55(7): 1079–1086. DOI:10.1007/s11430-012-4446-8 |
| [3] | 罗璠, 李建文, 黄海, 等. BDS广播星历的轨道误差分析[J]. 测绘通报, 2015(2): 70–72. |
| [4] | 楼益栋, 施闯, 葛茂荣, 等. GPS卫星实时精密定轨及初步结果分析[J]. 武汉大学学报(信息科学版), 2008, 33(8): 815–841. |
| [5] | 刘志强, 王解先. 广播星历SSR改正的实时精密单点定位及精度分析[J]. 测绘科学, 2014, 39(1): 15–19. |
| [6] | ØRPEN O, MELGAARD T.Experiences with Fugro's Real Time GPS/GLONASS Orbit/Clock Decimeter Level Precise Positioning System[C]//Dynamic Positioning Conference.Houston:Sensors, 2009. |
| [7] | GLOCKER M, LANDAU H, LEANDRO R, et at.Global Precise Multi-GNSS Positioning with Trimble Centerpoint RTX[C]//Satellite Navigation Technologies & European Workshop on GNSS Signals & Signal Processing.Noordwijk:IEEE, 2012:1-8. |
| [8] | ZHANG Q, MOORE P, HANLEY J, et al. Auto-BAHN:Software for Near Real-time GPS Orbit and Clock Computations[J]. Advances in Space Research, 2007, 39(10): 1531–1538. DOI:10.1016/j.asr.2007.02.062 |
| [9] | WEISS J P, BARSEVER Y, BERTIGER W. Near Real Time Precise Orbit and Clock Determination for GLONASS[J]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2010, 7672(6): 2771–2777. |
| [10] | 施闯, 楼益栋, 宋伟伟, 等. 广域实时精密定位原型系统及初步结果[J]. 武汉大学学报(信息科学版), 2009, 34(11): 1271–1274. |
| [11] | 陈明, 武军郦, 李志才. 北斗精密定轨及广播星历轨道精度评估[J]. 测绘工程, 2016, 25(11): 1–6. |
| [12] | 赵齐乐. GPS导航星座及低轨卫星的精密定轨理论和软件研究[D]. 武汉: 武汉大学, 2004. http://d.wanfangdata.com.cn/Thesis/Y698850 |
| [13] | 李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10486-1011404080.htm |
| [14] | 郝金明, 刘伟平, 杨力, 等. 北斗卫星导航系统精密定轨技术研究现状[J]. 测绘科学技术学报, 2015, 32(3): 221–225. |
| [15] | 崔红正, 唐歌实, 宋柏延, 等. 北斗卫星导航系统实时定轨与钟差处理策略[J]. 中国空间科学技术, 2015, 35(5): 1–7. DOI:10.3780/j.issn.1000-758X.2015.05.001 |
| [16] | 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005. |
| [17] | 谭畅, 陈国, 魏娜, 等. iGMAS轨道产品综合及精度初步分析[J]. 武汉大学学报(信息科学版), 2016, 41(11): 1469–1475. |
| [18] | ZHANG L P, DANG Y M, XUE S Q, et al. The Optimal Distribution Strategy of BeiDou Monitoring Stations for GDO Precise Orbit Determination[M]. Berlin: Springer, 2015: 153-161. |