2. 中国科学院国家天文台, 北京 100190
2. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100190, China
卡尔曼滤波(Kalman filtering)方法[1]对卫星导航定位具有重要意义。基于物体运动遵循惯性定律这一基本事实,它利用合适的运动模型,将相邻时刻的位置状态联系起来,从而克服最小二乘法在不同时刻的定位值互不关联这一缺点,将原本孤立杂乱的解结合起来,使滤波定位结果更为平滑和准确[2-4]。因此,卡尔曼滤波及其扩展卡尔曼滤波[5]、线性化卡尔曼滤波[6]、不敏卡尔曼滤波[7]等在卫星导航中得到了广泛的应用,并不断发展完善。
卡尔曼滤波通过状态方程一步转移实现系统状态的预测与更新,能够实时获得用户位置。然而,它在“跟随(tracking)”与“平滑(smoothing)”两个特征之间仍然存在着矛盾。实际应用中,往往通过调整滤波参数来实现这种平衡。如通过将滤波中状态噪声或测量噪声的协方差矩阵系数刻意调大,可降低测量值权重[8-9],从而使滤波结果更加平滑。但一方面,为保证良好的跟随性,反映出最小二乘解的真实性,滤波结果往往容易显得不够平滑,仍具有最小二乘解的杂乱性;另一方面,为追求良好的平滑性,使滤波结果更为美观,则又容易导致其偏离用户真实位置,产生“失真”的感觉。
基于卡尔曼滤波原理的延时平滑方法能够很好地解决这一问题。与根据经验和测试结果人为调整滤波参数不同,延时平滑方法从卡尔曼滤波模型出发进行理论公式推导,具有严谨的数学性,能够根据后续测量值及定位结果进行反馈与修正,达到对整个定位过程再次平滑的目的。它适用于许多对实时性要求不甚敏感的导航应用领域,如静止定位、行人定位、健康与运动监测、交通路况分析与规划等;甚至在实时车载定位的某些情况下,由于车辆并非一直处于高速行驶状态,因此也能够获得应用。
本文从卡尔曼滤波基本原理出发,介绍卡尔曼滤波延时平滑方法,分析和讨论其理论推导过程,并由此提出一类卫星导航定位中的卡尔曼滤波延时平滑方法。该方法能够根据后续历元测量值及定位结果向前进行逆向预测与更新,具有状态系统与测量系统两类方程;能够获得跟随与平滑之间的良好平衡,使定位结果更加准确和平滑。此外,由于可以使用后续状态量及测量值,因此方法具有更高的抗多径和抗遮挡性,能够进一步提高定位精度与性能。最后,通过静止定位、动态定位等多种不同情况下的GPS实测试验,对该方法进行分析与验证,以证明其正确性与可行性。
1 卡尔曼滤波定位方法 1.1 卡尔曼滤波回顾卡尔曼滤波自1960年被提出以来,不断得到完善和发展,已广泛应用于各个领域的信号与数据处理中。有关卡尔曼滤波的文献也相当丰富,且涉及随机变量、随机过程等多方面的知识和内容。因此,本文在此仅作简要回顾,不作具体推导。
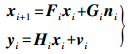 (1)
(1) 式中,xi、yi分别为系统状态与测量向量;ni、vi分别为状态噪声与测量噪声向量;Fi、Gi与Hi分别为系统状态转移矩阵、输入关系矩阵与测量关系矩阵。卡尔曼滤波假定ni和vi为零均值、不相关的高斯白噪声,即满足
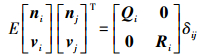 (2)
(2) 式中,Qi、Ri分别为ni和vi的协方差矩阵;δij为克罗内克函数(Kronecker Delta)。
那么从系统状态及均方误差初值x0、P0开始,卡尔曼滤波可利用如下一套包括3个测量更新方程和2个时间更新方程在内的数学递推公式对系统状态xi进行最优估计,使状态估计值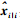
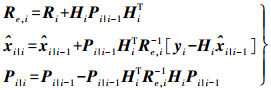 (3)
(3) 时间更新方程
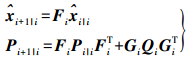 (4)
(4) 式中,Pi|j为系统状态估计误差
卫星导航遵循所有运动物体都符合牛顿定律这一基本事实,因此卡尔曼滤波定位模型可通过对不同运动特点的用户采用不同的状态方程模型来进行描述和实现。运动状态方程既要尽可能真实、完整地描述用户运动状态,又要控制状态向量的维数,减少计算量。
对于行人、汽车、舰船等低动态载体而言,其运动状态一般可用8个状态变量来描述,即3个位置分量(x, y, z)、3个速度分量(vx, vy, vz)和2个接收机钟差变量(δtu, δfu)。该运动模型因不考虑载体机动因素,因此又称为常速运动模型。其状态向量为[2, 12-14]
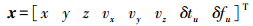 (5)
(5) 根据所采用的运动状态模型,其常系数状态转移矩阵F为
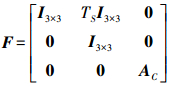 (6)
(6) 式中,TS为采样周期;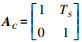
状态噪声协方差矩阵Q为
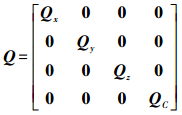 (7)
(7) 式中,Qx、Qy与Qz分别为X、Y与Z坐标分量上的位置与速度状态向量所对应的协方差矩阵,且具有相同的形式,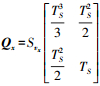
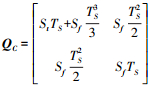
在实际应用中,准确确定状态量噪声与测量值噪声的均方误差Q、R并不容易。对于状态噪声误差Q,一方面可参考接收机说明书及性能测试指标等有关数据,另一方面可对此噪声信号作自相关运算来进行估计。而对于测量值噪声误差R,可根据导航电文中的URA值、卫星仰角、信号强度、接收机信号跟踪状况等信息进行估算,在实践中也可通过试验来测定测量误差方差,然后建立一个关于信号信噪比或卫星仰角的测量误差方差函数[2, 12]。
2 卡尔曼滤波时延平滑方法 2.1 固定时刻平滑根据式(4)中的卡尔曼滤波时间更新方程,可递推得知当i0>i时有[10]
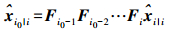 (8)
(8) 式(8)即可视为利用状态转移矩阵对状态量未来的状态进行i0-i步预测。现在, 反过来考虑i0 < i的情况,即利用状态过程中的后验测量数据对之前先验状态量进行修正与更新。已知在时刻j,测量值yj的修正量为
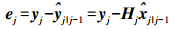 (9)
(9) 其协方差矩阵为
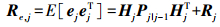 (10)
(10) 由修正量的正交性原则可推导得[15]
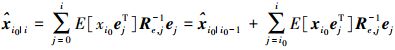 (11)
(11) 式中,当j≥i0时有E[xi0 ejT]= Pi0, j HjT。进而可推导得其状态量方差Pi0|i
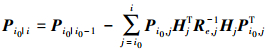 (12)
(12) 对于如式(1)给出的一个标准的状态空间模型,当j≥i时有
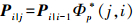 (13)
(13) 式中,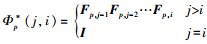
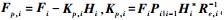
对式(13)进行矩阵求逆可得
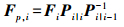 (14)
(14) 再定义矩阵
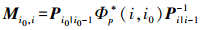 (15)
(15) 由此,即可以对式(10)和式(11)中的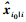
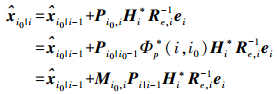 (16)
(16) 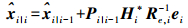 (17)
(17) 将式(17)代入式(16)可得
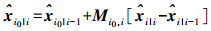 (18)
(18) 式(18)即为对于一个观测值给定至历元i的卡尔曼滤波器,估算其在之前某固定时刻i0的状态值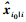
由式(12)和式(3)、式(4)可得当i≥i0时有
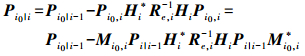 (19)
(19) 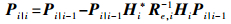 (20)
(20) 结合式(19)、式(20)可得协方差矩阵
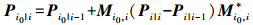 (21)
(21) 为计算矩阵M的递推公式,由式(13)—式(15)可推导得到
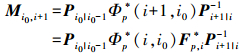 (22)
(22) 再将式(15)代入式(22)即有
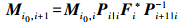 (23)
(23) 联立式(18)、式(21)和式(23),即得到一套用来计算对于一个观测值给定至历元i(i>i0)的卡尔曼滤波器在其之前某固定时刻i0的状态值的递推公式。其初始值为卡尔曼滤波所提供的状态量预测值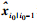
以固定时刻平滑方法为基础,可以推导得到另一种平滑计算方法:固定时延平滑。它用来求解一个给定观测量至历元i的卡尔曼滤波器在其之前L个固定历元(即i-L历元处)的状态值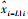
在历元i,卡尔曼滤波公式提供了状态量时间更新值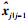
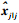
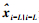
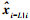
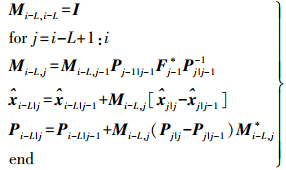 (24)
(24) 式中,协方差P提供了平滑值的误差特征情况。事实上它只是数学上的存在,在整个递推计算过程中是非必需的,但实际使用中也可利用它进行数值正确性的监测与检验。
2.3 卡尔曼滤波时延平滑定位流程无论是固定时刻平滑还是固定长度平滑,都基于基本的卡尔曼滤波方法,只是需要卡尔曼滤波过程不断提供在历元j(j=i-L, …, i)的状态量时间更新值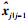
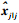

|
| 图 1 卡尔曼滤波延时平滑计算流程 |
卡尔曼延时平滑定位方法既可应用于静止定位情况,也可应用于车载定位等动态情况,以及定位数据事后处理与分析等领域。
以静止定位数据处理为例,往往通过对一段时间的定位数据取平均来获得当前位置更精确的坐标值。然而,由于接收机测量精度及卫星星座几何分布都并非固定不变的,因此定位结果之间往往并不具有相同的误差分布,从而使得这种笼统的均值处理方法显得过于粗糙。另外,由于缺乏误差特征指标,因此当测量或定位出现粗差时也难以及时发现。基于卡尔曼滤波原理的平滑计算方法则不同,它具有严谨的数学原理及模型,不同时刻的测量精度及卫星分布信息均包含在协方差矩阵Pj|j-1和Pj|j中。因此,在连贯的误差指标指引下,它能够获得最优的递归最小二乘平滑结果,并且具有较强的抗差性。
3 试验与分析利用搭载由中科微电子有限公司研制与提供的ATGM332D定位芯片的卫星导航接收机模块,以1 Hz频率通过串口传输方式输出GPS卫星广播星历及单频、C/A码伪距观测数据。基于该模块及其测量输出进行Arm编程实现,并在北京市中科院奥运村科学园区进行实时定位试验。
3.1 静止定位试验首先,在园区已知坐标点上进行了时间约2 h的静止定位测量,按照图 1中流程分别采用固定延时L为1、5、10及30 min的卡尔曼延时平滑方法进行处理,并将其与实时卡尔曼滤波定位结果相比较,如图 2所示。
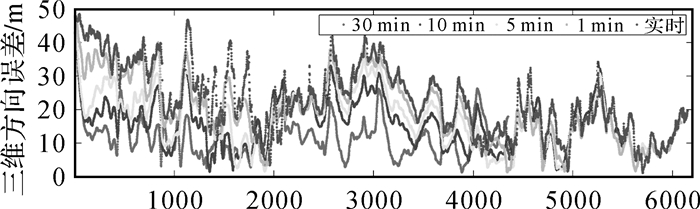
|
| 图 2 静止定位结果比较 |
统计各类处理方法误差特征,结果见表 1。
| m | |||||
| 类别 | 方法 | ||||
| 实时 | 1 min | 5 min | 10 min | 30 min | |
| X方向 | 10.7 | 9.4 | 8.5 | 8.0 | 4.6 |
| Y方向 | 19.2 | 18.1 | 15.1 | 13.4 | 9.0 |
| Z方向 | 12.3 | 9.2 | 8.5 | 8.1 | 6.5 |
| 三维方向 | 25.2 | 22.3 | 19.3 | 17.6 | 12.0 |
图 2及表 1中的试验结果验证了该方法的正确性和有效性。从中也可以看出,该方法特别适用于静止定位处理领域,能够显著改善定位精度。并且,其效果一般与延时时间成正比;随着可容忍的延时时间的增加,定位精度也随之提高。
3.2 动态定位试验同样基于固定时延平滑方法在中科院奥运村园区的道路上进行了车载定位试验,并实时计算和显示定位结果。然后,分别采用固定延时L为1、3、10 s的卡尔曼延时平滑方法进行处理,并与实时卡尔曼滤波定位结果相比较,如图 3所示。

|
| 图 3 动态定位结果比较 |
从图 3可以看出,即使固定延时仅为1个历元,平滑结果与实时滤波定位结果之间仍然具有一定的区别,但效果还不够明显。而当延时时间增加至10个历元时,即可明显看出两者之间的差别,从图 3中所标识的1、2、3、4号等位置观察得尤为明显。其中,固定时延平滑结果要比实时滤波定位结果更平滑,与实际行驶道路更为吻合,抗遮挡及多径环境的性能也更加优秀。
4 结论在导航数据处理中,需要追求定位结果跟随性与平滑性之间的平衡。即在使得位置结果尽量平滑、准确和美观的同时,又不损失用户真实运动轨迹的细节特征,不造成失真。卡尔曼滤波延时平滑方法可以很好地解决这个问题,它具体包括固定时刻平滑与固定时延平滑方法。与人为根据经验和测试结果去调整滤波器参数不同,延时平滑方法同样具有状态更新和时间更新两类系统和方程,相当于再逆向进行了一次卡尔曼滤波过程,具有严谨的数学性。
具体而言,这种卡尔曼滤波延时平滑定位方法具有以下几个特点:
(1) 由卡尔曼滤波理论出发推导得到,其原理和形式均与经典卡尔曼滤波方法保持一致,数学上严谨、规范。
(2) 与人为调整和修改参数不同,通过向前逆向预测和更新来对先验历元定位进行平滑,能够在进一步平滑结果、减小随机误差的同时,不造成平滑过度和失真。
(3) 在计算量与耗时上,由于延时平滑方法递推公式基于状态一步转移,因此可以很快向前计算,不会造成明显计算负荷。
(4) 模型时延长度可根据实际应用情况进行适应与更改。
通过不同情况下的GPS实测试验,验证、分析了卡尔曼滤波延时平滑定位方法的正确性和可行性。它不仅能够在静止定位或数据后处理时大幅提高定位精度、缩短工作时间,还能在行人、车载等实时动态定位领域根据实际情况调整延时长度,更好地获得定位结果跟随与平滑之间的平衡,并同时具有更强的抗多径与遮挡的能力。该方法原理严谨、易于实现,具有良好的实用效果与价值。
| [1] | KALMAN R. A New Approach to Linear Filtering and Prediction Problems[J]. Transactions of ASME-Journal of Basic Engineering, 1960(82): 34–45. |
| [2] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. |
| [3] | SORENSON W. Least-squares Estimation:from Gauss to Kalman[J]. IEEE Spectrum, 1970, 7(7): 63–68. DOI:10.1109/MSPEC.1970.5213471 |
| [4] | TED B, RAMA C. Estimation of Object Motion Parameters from Noisy Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(1): 90–99. |
| [5] | WELCH G, BISHOP G.An Introduction to the Kalman Filter[M].Ashville:University of North Carolina, 2004. |
| [6] | FARRELL J, BARTH M.The Global Positioning System and Inertial Navigation[M].New York:McGraw-Hill, 1999. |
| [7] | JULIER S, UHLMANN J.A New Extension of the Kalman Filter to Nonlinear Systems[C]//Proceedings of AeroSense:The 11th International Symposium on Aerospace/Defense Sensing, Simulation and Controls.Orlando, FL:[s.n.], 1997:192-193. |
| [8] | GREWAL M, ANDREWS A.Kalman Filtering:Theory and Practice Using MATLAB[M]. 2nd ed. New York:John Wiley & Sons, Inc, 2001. |
| [9] | 季海福. 基于SIGSO同行卫星的导航星座原理与算法研究[M]. 北京: 中国科学院国家天文台, 2013. |
| [10] | CATTIVELLI F, SAYED A. Diffusion Strategies for Distributed Kalman Filtering and Smoothing[J]. IEEE Transactions on Automatic Control, 2010, 55(9): 2069–2084. DOI:10.1109/TAC.2010.2042987 |
| [11] | SAYED H, KAILATH T. A State-space Approach to Adaptive RLS Filtering[J]. IEEE Signal Processing Magazine, 1994, 11(3): 18–60. DOI:10.1109/79.295229 |
| [12] | PARKINSON B, SPILKER J, AXELRAD P, et al.Global Positioning System:Theory and Applications[M].[S.l.]:American Institute of Aeronautics and Astronautics, 1996. |
| [13] | LEANDRO R, SANTOS M. Stochastic Models for GPS Positioning:An Empirical Approach[J]. GPS World, 2007. |
| [14] | HIDE C, MOORE T, HILL C, et al. Low Cost, High Accuracy Positioning in Urban Environments[J]. Journal of Navigation, 2006, 59(3): 365–379. |
| [15] | KAILATH T, SAYED H, HASSIBI B.Linear Estimation[M].New Jersey:Prentice Hall, 2000. |
| [16] | KELLY C, ANDERSON B. On the Stability of Fixed-lag Smoothing Algorithms[J]. Journal of the Franklin Institute, 1971, 291(4): 271–281. DOI:10.1016/0016-0032(71)90183-9 |
| [17] | CATTIVELLI F, LOPES C, SAYED A.Diffusion Strategies for Distributed Kalman Filtering:Formulation and Performance Analysis[C]//Proceedings of Cognitive Information. Santorini:[s.n.], 2008. |


