合成孔径雷达干涉(synthetic aperture radar interferometry,InSAR)技术使用对同一地区进行重复观测的两景SAR影像获取地表的高程或形变信息。InSAR最初被用于金星的地形测量,并在1974年首次应用于地球地形测绘[1]。现阶段,使用InSAR技术的航天飞机雷达地形测绘任务(shuttle radar topography mission,SRTM)已经可以提供全球纬度范围-56°至60°内的16 m高程精度数字高程模型(digital elevation model,DEM)[2]。使用TanDEM-X编队卫星获取的DEM更是将覆盖范围扩展到南极,全球范围内90%点对点高程精度达到了3.49 m以内[3]。
国内外已经针对InSAR地形测绘开展了较多的研究。例如,德国宇航局的学者针对TanDEM-X卫星进行了详细的误差分析,并面向星上和地面定标技术开展了大量的先期技术探讨和论证。这种星地一体化的论证方式,共同保障了TanDEM-X的测绘精度[4]。国内也有学者曾采用简单的机载模型进行了InSAR地形测绘的误差分析[5],但是模型未考虑地球曲率的影响,现阶段普遍采用更为通用的星载分布式InSAR的误差分析模型[6],然而其中基线依然是机载模型的基线表达方式,只考虑了长度和倾角。此外,国内针对机载InSAR技术也作过部分干涉定标研究,而面向星载InSAR的干涉定标技术受到数据质量的限制,研究相对较少。
本文面向分布式星载InSAR在地形测绘中的应用,研究卫星的8个直接观测量,并给出观测量在地形测绘中的误差传播公式。这8个观测量包括主星三维位置矢量、斜距、基线三维矢量以及相位。本文将其定义为一级误差源,并对一级误差源进行分解,给出对应的二级误差源。
1 卫星形成干涉的前提条件我国已经发射了两颗民用SAR卫星,即环境-1C和高分三号。然而这两颗卫星的干涉性能并不理想,想要满足业务化的干涉需求,还需要更进一步的约束条件。本节对SAR卫星形成干涉的前提条件进行了定量化分析。
两个回波信号能够形成干涉的条件是两者在地物上有足够的方位向和距离向信号带宽重叠度,即足够高的相干性。相干性可表述为
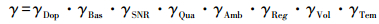 (1)
(1) 式中,右边八项分别为多普勒相干性、基线相干性、信噪比相干性、量化相干性、模糊相干性、配准相干性、体散射相干性及时间相干性。对于TanDEM-X来说,某些相干性的典型值为γSNR=0.975,γQua=0.96,γAmb=0.94,γReg=0.984,这几项总的相干性为0.866[4],体散射相干性与地物相关,而时间相干性在单发双收模式中可认为是1。在信噪比、量化、模糊以及配准失相干较小的情况下,式(1)的相干性约束条件中,就仅剩多普勒相干性及基线相干性与卫星相关。这两个参数是现阶段进行国产卫星相干性约束的重要参数。
主辅影像瞬时多普勒差异的表达式为
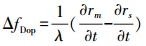 (2)
(2) 式中,λ为波长;rm为主影像斜距;rs为从影像斜距。对于TanDEM-X来说,主辅影像成像时刻的速度大小差异小于1 m/s,速度方向差异小于0.001°,对应的偏航角小于4°,俯仰角小于0.1°,此时可将式(2)变换为[4]
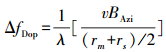 (3)
(3) 式中,BAzi为方位向基线长度;v为卫星速度。而多普勒相干性一般表达为
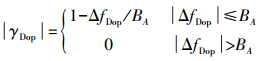 (4)
(4) 式中,BA为方位向处理带宽。对于TanDEM-X来说,若假设方位向相干性为0.9,设置方位向处理带宽为2000 Hz,若其飞行速度为7 687.06 m/s,斜距为621 709.05 m,那么对应的沿轨基线约485.26 m。值得说明的是,对于SAR来说,一般在成像过程中会将多普勒中心归零,称之为零多普勒中心成像,这种情况下,相干性将不再受沿轨基线的限制。此时需要约束的主要参数,就是垂直基线的相干性,也称为基线的相干性。
垂直基线的表达式为[7]
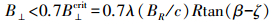 (5)
(5) 式中,BR为距离向带宽;c为光速;β为本地入射角;ζ为本地坡度角。距离向带宽与距离向分辨率μr相关,即
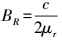 (6)
(6) 如果设置距离向分辨率为2 m,入射角35.97°,本地坡度角为0°,那么对应的垂直基线应小于2 368.80 m,然而此时的基线相干性只能达到0.3。虽然这种相干性能够满足相位解缠的最低要求,但并不能确保地形测绘精度。在地形测绘过程中,一般需要使用高程模糊度(height of ambiguity,HoA)对基线进行进一步约束,HoA表达为
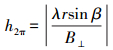 (7)
(7) TanDEM-X采用了两期的HoA设置,第一期为40~55 m,第二期为35 m[8],即HoA在35~55 m之间,得到垂直基线的范围为199.18~313.00 m。
综合以上分析发现,想要实现SAR卫星的干涉,主要需要从载荷及平台两个层面进行相干性约束。考虑到美国1978年发射的SeaSat已经可以提供干涉图,因此研究认为,经过将近40年的发展,载荷技术已经不是国产SAR卫星长期以来无法进行干涉的主要制约因素。而平台的控制,特别是垂直基线长度的控制,是现阶段国产SAR卫星进行业务化干涉的主要瓶颈。
2 InSAR地形测绘观测模型及误差分析 2.1 地形测绘模型使用InSAR进行地形测绘时的观测几何如图 1所示。为了便于表述,对部分参数的比例进行了夸张。其中S1为主影像对应的天线相位中心位置,S2为从影像对应的天线相位中心位置,B为基线长度,a为基线倾角,θ为侧视角,B⊥为垂直基线,r和r+Δr分别为主从影像天线相位中心到地面点P的距离,H为卫星高度,RH为卫星到地心的距离,Rh为地面点到地心的距离,Re为地球曲率半径,h为地面点高程。根据余弦公式,h可表达为
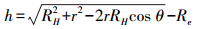 (8)
(8)
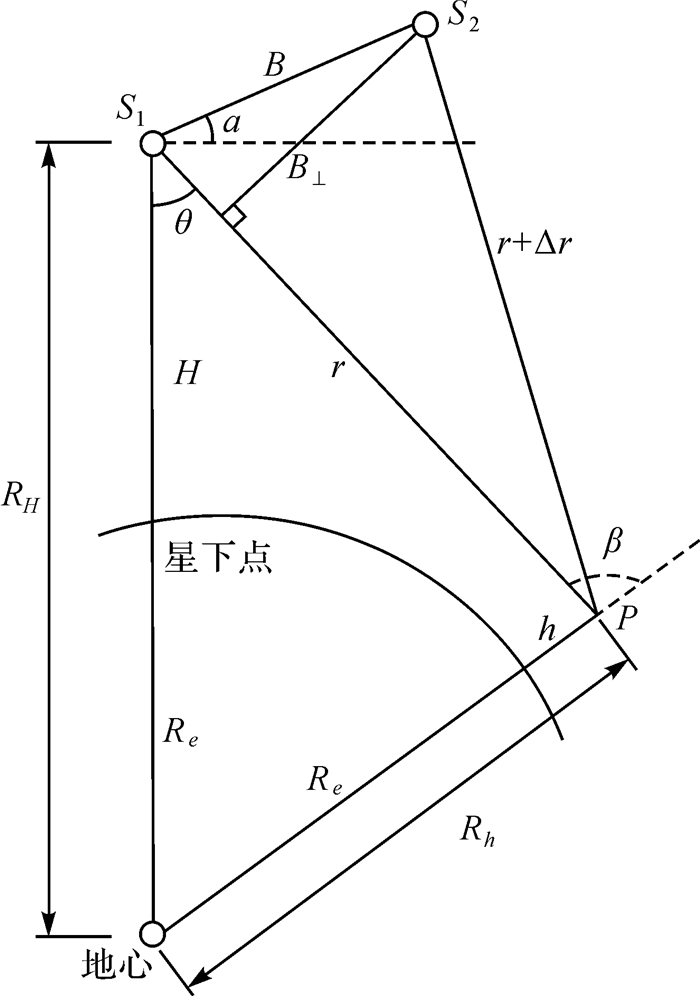
|
| 图 1 InSAR在地形测绘中的观测几何 |
对定轨参数(X, Y, Z)、基线三维分量(BX, BY, BZ)、斜距参数r和非缠绕相位ϕ求偏导之后,可得到各误差分量对高程的误差传递模型,即
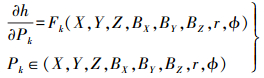 (9)
(9) 总的高程精度是各误差分量的几何平均,即
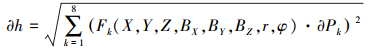 (10)
(10) 表 1以陕西省渭南市2011年11月26日成像的升轨TanDEM-X影像中心点为例,给出了各个观测量的误差大小及对应的高程误差。
| 参数 | 观测值 | 误差值 | 高程误差/m |
| λ | 0.03 m | — | — |
| Re | 6 371 419.05 m | — | — |
| h | 427.60 m | — | — |
| X1 | -1 558 440.56 m | 0.20 m | 0.05 |
| Y1 | 5 509 537.07 m | 0.20 m | 0.16 |
| Z1 | 3 821 829.18 m | 0.20 m | 0.11 |
| Bx | 0.51 m | 0.006 m | 6.98×10-6 |
| BY | -300.26 m | 0.006 m | 7.01 |
| BZ | 561.13 m | 0.006 m | 5.08 |
| r | 621 709.05 m | 1.00 m | 2.32 |
| φ | 1 218 648.6° | 20.00° | 2.49 |
| 合计 | 9.31 m | ||
由上述表述可知,InSAR地形测绘中的一级误差可分为4类。这4类误差中,主星定轨误差为次要误差,基线测量误差、斜距误差及相位误差为主要误差源。本节对一级误差进行了分解,给出了二级误差的来源。
2.2.1 主星定轨误差卫星定轨采用的是星上GPS数据,星上实时定轨精度一般在8.7~10.0 m,而经过事后处理,定轨精度一般能够达到5 cm左右。因此一般不再针对定轨数据进行额外检校。然而,对于500 km高度的卫星来说,1 ms的方位向时间误差会带来约7 m的定轨误差。几何检校过程中,需要针对方位向时间误差开展精确的测量和补偿。
2.2.2 基线测量误差TanDEM-X为分布式干涉SAR系统,其基线测量是通过双差GPS(double differential GPS,DDGPS)实现的,理论基线测量精度可达到1 mm[9]。然而,由于整周模糊度、各类坐标转换误差及姿态测量误差的影响等,实际的基线精度只能达到2~10 mm[9],假设三轴等精度观测,那么基线带来的高程误差将在1.70~8.49 m。在DDGPS基线测量中,主要的误差来源见表 2。
| 误差来源 | 二级误差来源 | 基线误差/mm | 高程误差/m |
| 从GPS天线相位中心到卫星质心的坐标转换误差 | GPS卫星轨道误差 | 0.002 5 | 0.002 12 |
| GPS载波相位观测噪声(1 mm) | 1.4 | 1.188 | |
| 卫星平台姿态测量误差(慢变误差0.005°,测量标准差0.003°) | 0.47 | 0.399 | |
| GPS接收天线安装位置的地面标校误差(0.5 mm) | 0.71 | 0.602 | |
| 从卫星质心到大地坐标系的转换 | 卫星平台姿态测量误差 | 0.5 | 0.425 |
| SAR天线相位中心不一致 | 0.25 | 0.212 | |
| 总误差 | 1.73 | 1.468 |
由于基线三维矢量对高程的传递关系不是非常直观,可以将基线三维矢量转换为沿轨基线、平行基线及垂直基线三分量。其中,沿轨基线在交轨干涉中不予考虑。平行基线误差对高程误差的传递关系可表达为[9]
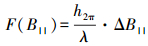 (11)
(11) 式中,B||为平行基线。对于X波段来说,1 mm的平行基线误差可能带来0.15 m的高程误差(h2π=35 m)。垂直基线与高程之间的转换关系可表达为
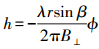 (12)
(12) 依据基线转换公式,有
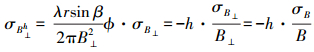 (13)
(13) 高程的误差与高程本身相关,高程越大,对应的误差越大。由此可知,对于同样的观测条件来说,平地、丘陵、山地与高山地的精度将会各不相同。假设基线的测量精度为1 cm,基线长度为636 m,那么高程为10、100、1000 m时,对应的高程误差分别为0.157、1.57、15.7 mm。
2.2.3 斜距测量误差雷达到目标的斜距是通过记录接收脉冲相对于发射脉冲的时延来确定的,因此斜距测量误差主要来源于计时系统的误差,包括雷达计时系统的不确定性、采样时钟的抖动和电波通过大气及电离层的延时等。对于TanDEM-X来说,定标之前的时间误差可为212 ns,约31.8 m。定标之后斜距测量误差则优于3.75 cm,最终的定位精度则能够控制在30 cm以内[10],几乎比标称精度(2 m)高出一个数量级。按照定标之后的精度推算,斜距带来的高程误差为0.087 m,其影响几乎可以忽略不计。
2.2.4 相位误差相位误差的来源较多,从InSAR的整个信号传输链路和误差的特性上看,大致分为系统性误差和随机性误差。
系统性误差是慢变型误差,其频率为1 Hz甚至更小。其中较为典型的误差包含相位漂移、相位同步误差、温度误差等。对于TanDEM-X来说,相位漂移误差一般在3°左右,定标后优于1°[10]。相位同步误差是由于双星各自采用不同的晶振带来的晶振频率偏差及部分相位噪声误差,通过星上的信息同步以及地面成像过程中的信息补偿,相位同步误差一般可控制在5.5°左右[11]。内定标回路的脉冲会受到温度变化的影响,以TanDEM-X为例,一景影像的获取时间内,温度变化为10℃,这在极端情况下会带来2.5°的相位误差,对高程的影响约0.31 m,这种高频误差项可在星上采用高阶多项式进行拟合,并在定标脉冲发出时及时进行消除,因此一般不作为主要误差考虑[12]。
随机性误差的来源主要是失相干误差。失相干误差主要包含式(1)中的8类,同样以阎良地区的TanDEM-X为例,8类相干性分量及其对应的高程误差见表 3[4]。
| 误差来源 | 相干性 | 相位误差/(°) | 高程误差/m |
| 多普勒相干性 | 0.989 | 6.16 | 0.77 |
| 基线相干性 | 0.94 | 10.15 | 1.26 |
| 信噪比相干性 | 0.975 | 9.23 | 1.15 |
| 量化相干性 | 0.96 | 11.82 | 1.47 |
| 模糊相干性 | 0.94 | 10.15 | 1.26 |
| 配准相干性 | 0.96 | 11.82 | 1.47 |
| 体散射相干性 | 0.95 | 13.32 | 1.66 |
| 时间相干性 | 1 | 0 | 0 |
多普勒失相干对于零多普勒中心成像来说,几乎可以忽略。然而零多普勒成像会导致天线最大增益有所降低,同时天线的指向误差也会带来最大增益的损失。对于TanDEM-X来说,1 km沿轨基线长度会降低0.5 dB,0.01°的天线指向误差会降低0.1 dB,这部分误差造成多普勒相干性为0.989,这种失相干现象与沿轨基线几乎没有太大的相关性[4]。
基线失相干与成像几何相关,结合式(5)—式(7)可知,如果本地坡度角为0°,则
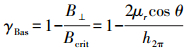 (14)
(14) 此时,高程模糊度越大,相干性越好。而高程模糊度越大,意味着垂直基线越小,这与式(13)中需要的长基线恰恰相反。因此,InSAR地形测绘过程中,基线不能过短,也不能过长,一般需要约束HoA使其在35~55 m,此时基线相干性在0.908~0.941之间。
信噪比失相干的决定性参数是噪声等效散射系数(noise equivalent sigma zero,NESZ)。对于TanDEM-X来说,NESZ使用接收信号进行估测[7]。实际上,地物类型的不同,侧视角度的不同,都会对信噪比造成一定的影响。一般来说,相干性由高到低的顺序是岩石土壤、森林、雨林、沙漠、水体。而侧视角越小,相干性越大,如侧视角由48°减小到32°时,相干性可能会增加60%左右。若以岩石土壤做约束,信噪比相干性一般需要达到0.975以上[4]。
量化失相干是对模数转换的SAR信号进行区域自适应量化(block adaptive quantization,BAQ)的过程中,由BAQ的有损压缩特征带来的信号失相干。一般可选的压缩比有8:2、8:3、8:4、8:6以及8:8。压缩比越大,失相干越大,高程精度越差。对于TanDEM-X来说,第一年的观测过程中,量化比一般选择为8:3或者8:4,相比于8:8来说,其相干性损失约为3.5%和1%,带来的高程误差为厘米级。第二年观测时,由于已经有第一年的数据积累,可适当缩小量化比,如选择为8:3(TDX)和8:2(TSX),也并不会对高程带来较大的影响[13]。
模糊失相干分为方位向模糊及距离向模糊。其中距离向模糊基本可以忽略,而方位向模糊与脉冲重复频率(pulse repetition frequency,PRF)相关,PRF越大,相干性越高。
配准的精度优于0.1个分辨单元时,配准相干性已经不会有明显的提升,此时的相干性一般为0.96[7]。
体散射失相干是植被较多的区域枝叶、枝干等在单一散射单元内的后向散射叠加带来的。通过控制卫星状态,使双星观测几何尽量一致,也即式(7)中高程模糊度尽量大,可以削弱体散射失相干的影响。在植被小于5 m,高程模糊度大于35时,可认为体散射相干性大于0.95[13]。
时间失相干在以测绘任务为主的单发双收交轨干涉模式中不予考虑,而采用顺轨模式进行海洋流速监测时,沿轨基线带来的时间基线应小于7 ms[4]。在重轨干涉中,时间失相干与波长和地物位置相关,如果入射角为35.97°,那么在L波段中,某分辨单元内部各散射体平面位置随机移动10 cm,相干性就会降为0.007,而在X波段中,约1.3 cm的平面位置变化就会导致相干性变为0.007[14]。
随机相位误差除了上述的相干性误差之外,还有数据处理过程中引入的误差,主要包括保相成像误差、插值误差以及解缠误差等。常用的保相成像算法中,BP算法的保相性最好,在平地或丘陵地区,其保相成像误差一般在3度以内[15]。常用的插值算法中,最邻近法的精度最差,带来的相位误差可能达到20°以上,而三次卷积及截断sinc函数插值的效果都会比较好,采用16点截断sinc函数插值引入的相位误差将优于2°。相位解缠误差则较难衡量,现阶段也没有较为可靠的经验公式,先期研究表明,高程模糊度控制在35~55 m时,如果高程落差小于1000 m,相位解缠误差可控制在10°以内。
2.2.5 其他误差TanDEM-X的双星干涉过程中,除了上述误差之外,还存在频率不一致的误差、穿透深度的误差、姿态的误差等。由于篇幅所限,本文不再针对这些误差作深入分析。
3 结语本文进行了星载InSAR地形测绘的误差来源分析。首先,给出了国产SAR卫星长期以来无法干涉的主要原因,即垂直基线长度无法有效控制在0.3倍极限基线以内;其次,给出了分布式InSAR卫星的误差模型,并使用真实的观测量对误差进行了定量分析,分析表明,在四类误差源中,基线误差和相位误差是InSAR地形测绘中的最主要误差源。
围绕国产InSAR卫星的指标体系论证,本文依然有诸多问题有待进一步研究,例如,如何选取最优基线,以便同时保障几何稳定性、基线相干性及相位解缠精度等;如何对二级误差源进行进一步分解,以便为卫星的设计提供指标参考;如何进行干涉测量检校算法设计,精确分解各观测参数误差。这些问题的解决对我国SAR卫星的指标设计有非常重要的意义。
| [1] | GRAHAM L C. Synthetic Interferometer Radar for Topographic Mapping[J]. Proceedings of the IEEE, 1974, 62(6): 763–768. DOI:10.1109/PROC.1974.9516 |
| [2] | USGS.Shuttle Radat Topography Mission[EB/OL].(2014-07-16)[2015-07-16].http://srtm.usgs.gov/mission.php. |
| [3] | BUCKREUB S.TerraSAR-X/TanDEM-X Mission Overview[C]//Proceedings of the TerraSAR-X/TanDEM-X Science Meeting. Oberpfaffenhofen:[s.n.], 2016. |
| [4] | KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X:A Satellite Formation for High-resolution SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3317–3341. DOI:10.1109/TGRS.2007.900693 |
| [5] | 张磊, 伍吉仓, 陈艳玲. InSAR高程模型及其精度分析[J]. 武汉大学学报(信息科学版), 2007, 32(2): 108–122. |
| [6] | 张永俊. 星载分布式InSAR系统的误差分析与DEM精度提高方法研究[D]. 长沙: 国防科学技术大学, 2011. http://d.wanfangdata.com.cn/Thesis_D201595.aspx |
| [7] | HANSSEN R F.Radar Interferometry:Data Interpretation and Error Analysis[M].[S.l]:Springer, 2001. |
| [8] | ROSSI C, RODRIGUEZ GONZALEZ F, FRITZ T, et al. TanDEM-X Calibrated Raw DEM Generation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73(9): 12–20. |
| [9] | HUESO G J, WALTER A J M, BACHMANN M, et al. Bistatic System and Baseline Calibration in TanDEM-X to Ensure the Global Digital Elevation Model Quality[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73(3): 3–11. |
| [10] | SCHWERDT M, GONZALEZ J H, BACHMANN M, et al.In-orbit Calibration of the TanDEM-X System[C]//Geoscience and Remote Sensing Symposium.Vancouver:IEEE, 2011:2420-2423. |
| [11] | 李世强, 禹卫东. 分布式卫星SAR相位同步的实现方案及实验验证[J]. 电子与信息学报, 2012, 34(2): 356–360. |
| [12] | GONZÁLEZ J H, BACHMANN M, KRIEGER G. Development of the TanDEM-X Calibration Concept:Analysis of Systematic Errors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 716–726. DOI:10.1109/TGRS.2009.2034980 |
| [13] | MARTONE M, BRÄUTIGAM B, RIZZOLI P, et al. Coherence Evaluation of TanDEM-X Interferometric Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 73(6): 21–29. |
| [14] | ZEBKER H A, VILLASENOR J. Decorrelation in Interferometric Radar Echoes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(5): 950–959. DOI:10.1109/36.175330 |
| [15] | 杨娟. 高保相毫米波干涉SAR技术研究[D]. 成都: 电子科技大学, 2012. |


