目前,GPS多路径误差的修正方法主要包括3大类:GPS天线设计、接收机信号处理及数据的后处理[1]。抑制多路径的GPS天线设计造价昂贵,且信号处理后残余的多路径误差也不容忽视,相对而言,数据后处理是一种较合理的方法。后处理方法一般包括:天线阵列法、信噪比法、反射信号计算法及重复性法[1-2]。在GPS静态测量中,接收机天线一般在很小的范围内活动,因此可认为多路径误差具有周日重复性,可用重复性模型进行多路径改正。
针对多路径周日重复性的特点,可利用小波滤波[3]、EMD滤波[4]、Vondrak滤波[5]及自适应滤波[6]等对多路径进行削弱。EMD滤波是由Huang等提出的一种时域信号处理方法[6-7],将信号分解为一系列从高频到低频的模态函数(IMF),能够有效提取信号的趋势项。但是EMD易受模态混叠效应的影响,即不同的模态出现在同一个模态函数中,或相同的模态被分解到不同的模态分量中,提取效果受观测数据的影响。完备经验模态分解算法(CEEMD)是对EMD算法的一种改进,它对每一阶分量加入特定的白噪声,通过求取残差来得到每个模量,在保证信号重构的完备性的同时,对模态混叠效应有一定的抑制作用[8]。然而对于高频信息采用直接滤出,容易造成信号失真,同时低频信号中也可能包含少量的噪声。Wavelet是信号降噪领域的常用方法,具有很好的时频分析性能,但去噪效果受小波基和阈值选择的影响。SavGol滤波是一种基于局域多项式的最小二乘拟合平滑算法[8],这种滤波器最大的特点是在消除噪声的同时保证信号的形状和宽度不变。
为了进一步对GPS多路径低频信息进行提取,本文分别采用Wavelet和SavGol滤波对高频和低频信息进行降噪,并对降噪后的模量进行重构,来获得多路径信息。最后将第一天的模型应用于第二天坐标序列修正中,对新模型进行验证。
1 GPS多路径提取相关模型 1.1 Wavelet模型Wavelet模型通过对序列进行降噪,达到提取多路径的目的。小波滤波的核心是小波变换,它的基本思想是用一族小波函数系去逼近信号。该小波函数系是由一基本小波函数通过平移和伸缩构成的。设基本小波函数为Ψ(t),平移和伸缩因子为a和b,则小波变换为原信号与小波基函数的内积[3, 5]
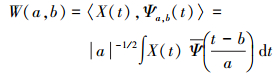 (1)
(1) 式中,W(a, b)表示小波变换系数;X(t)表示原始信号;Ψ(t)表示Ψ(t)的共轭。
在小波去噪中,一般根据经验或不断地试验选择小波基函数。本文选用db3小波基函数进行变换分析,对小波分解的高频系数进行阈值化处理后,进行小波重构信号,计算公式如下[5]
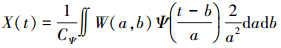 (2)
(2) 式中,CΨ表示小波的可容性条件。
1.2 CEEMD模型CEEMD是由TORRES等提出的一种EMD改进算法[9],其核心思想是在每一阶模量中加入白噪声,并且计算唯一残差得到每个模量。它的基本算法如下[9-11]:
(1) 向信号中加入M次不同的高斯白噪声,进行EMD分解,将每次分解得到的第一分量结果进行总体平均,得到原信号分解的第一模态分量IMF1,即
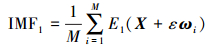 (3)
(3) 式中,Ei()为第i个模态分量;ε为噪声系数;ωi为具有单位方差的零均值白噪声。
(2) 计算一阶残差r1
 (4)
(4) (3) 对r1+εE1(ωi),i=1, 2, …, M,进行EMD分解,直到它们达到了EMD分解判断IMF的条件,并定义总体均值为IMF2,即
 (5)
(5) 对于k=2, 3, …, K,计算第k阶的残差,按照步骤(3)对rk+εEk(ωi)提取EMD分解的第一模态分量,并计算总体平均值为
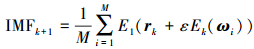 (6)
(6) 当残差极值点个数小于2时,筛选结束,最终得到信号的趋势项R。信号最终被分解为
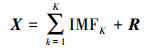 (7)
(7) 在分解完成之后按照尺度标准化模量累计均值(MSAM)进行噪声和有用信号的区分。若其值偏离零,则认为该尺度以上的高阶模量为系统趋势项。其计算公式为[4]
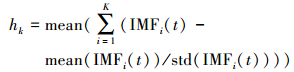 (8)
(8) 式中,hk为MSAM;K为分解尺度;IMFi(t)为第i尺度模量。
1.3 SavGol滤波SavGol滤波是由Savizky A和Golay M在1964年提出的一种数据流平滑降噪滤波器[12],该滤波器对每个数据点的邻域内各点的数据进行一元p次多项式拟合,多项式的系数按照最小二乘法来确定。
设X(t)为原始序列,邻域为[-M, N],则在每个数据点X(i)需构造一个p阶多项式p(t)来拟合M+N+1个数据点,进而得到该数据点的拟合值。在拟合时,不可避免产生拟合误差,为了保证拟合效果,需对[13]
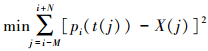 (9)
(9) 进行线性化,可得
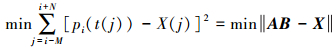 (10)
(10) 式(10)达到最优时,满足AB = X,按照最小二乘法进行求解,得
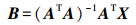 (11)
(11) 最后得到X的拟合值为
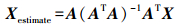 (12)
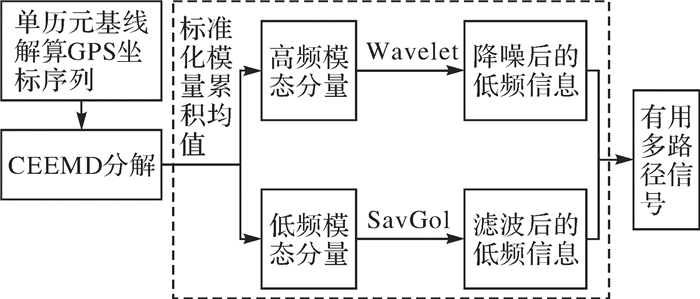
(12) CEEMD-Wavelet-SavGol模型综合利用这3种模型的优越性,将3种方法组合进行GPS坐标序列多路径的提取,流程如图 1所示。
|
| 图 1 CEEMD-Wavelet-SavGol提取多路径信号流程 |
为了能够定量确定多路径提取过程中的降噪效果,选用相关系数R、标准差σ和信噪比SNR作为评价指标,计算公式如下[1, 3, 14]
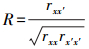 (13)
(13) 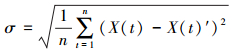 (14)
(14) 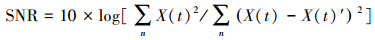 (15)
(15) 式中,X(t)为原始序列;X(t)′为去噪后序列;n为序列长度;rxx′为X(t)序列和X(t)′的协方差;rxx为X(t)序列的方差;rx′x′为X(t)′序列的方差。
2 试验及结果分析两天相同时段的GPS数据采集试验是在中国矿业大学环测学院楼顶进行的。采样频率为1 s,卫星高度截止角为10°,相邻两天天气晴朗,微风,观测条件差别不大。基站位于天台强制对中墩上,离反射物的距离较远,可以认为其不受多路径的影响。在基站的东南方向3 m处有建筑物遮挡,观测条件较差。由于移动站是一个固定点,因此,可认为坐标位移序列主要包括多路径误差和随机噪声。
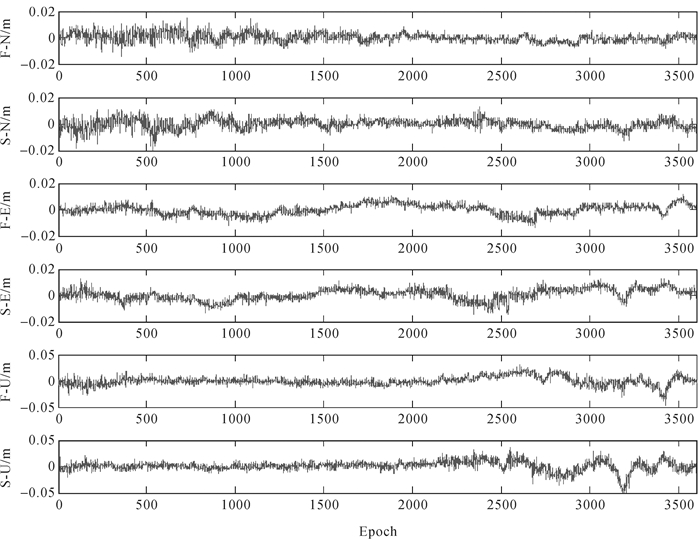
如图 2所示(F-N代表第一天的N方向,S-N代表第二天的N方向,其他类推,下同),依次为连续两天N、E和U方向的坐标位移序列。从图中可以看出,连续两天的N、E和U坐标位移序列的趋势一致,第二天相对于第一天有所提前,并且通过计算两天序列3个方向的相关系数分别为0.65、0.69、0.61,且分别出现在-235、-234、-231 s,与理论值-236 s是相符的。
|
| 图 2 连续两天N、E和U方向坐标位移序列 |
为了验证组合模型的有效性,采用4个方案对连续两天坐标序列进行分析:
方案1:基于Wavelet分解的多路径提取;
方案2:基于EMD的多路径提取;
方案3:基于CEEMD的多路径提取;
方案4:基于CEEMD、Wavelet和SavGol滤波的多路径提取。
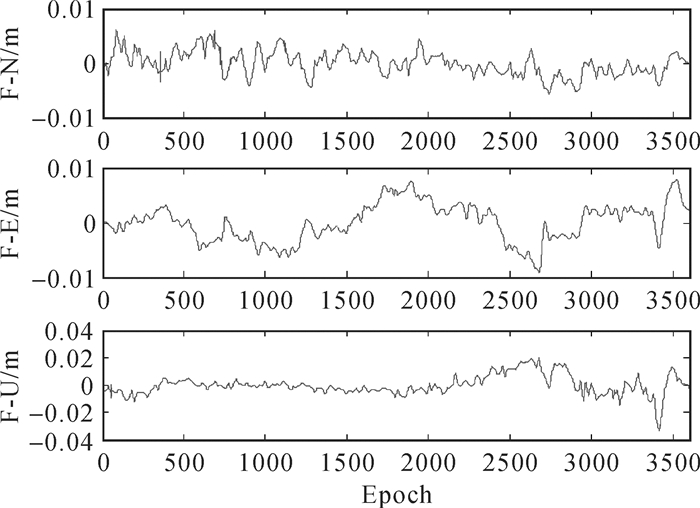
方案1采用db3小波基,对原始信号进行4层分解,采用自定义软阈值对高频小波系数进行处理,最后经过信号重构,得到去噪后的有用信号,如图 3所示(限于篇幅,所有方案第二天的多路径提取结果未列出)。
|
| 图 3 基于Wavelet分解的多路径提取序列 |
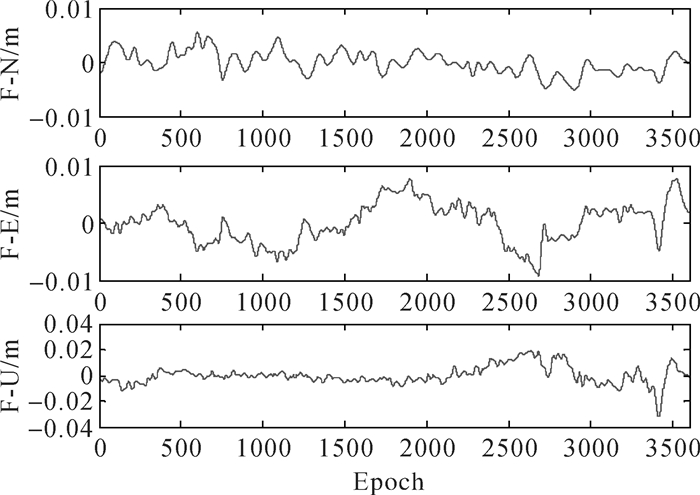
方案2采用EMD算法进行多路径提取。多路径提取后的序列如图 4所示。
|
| 图 4 基于EMD的多路径提取 |
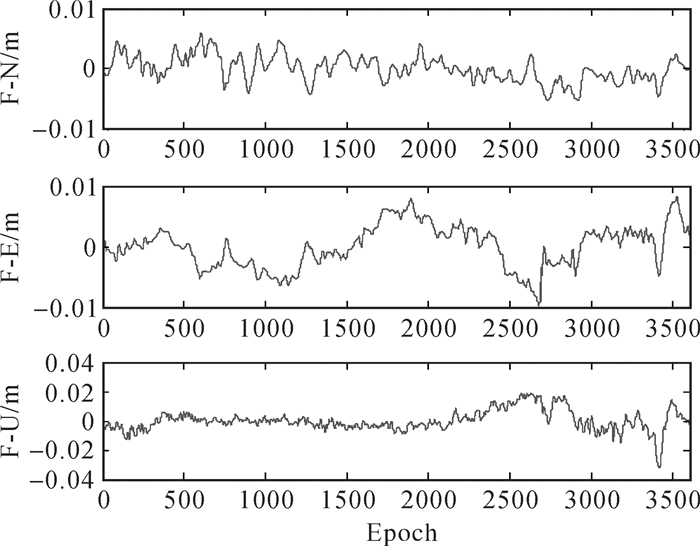
方案3采用CEEMD对原始信号进行多路径提取。对于第一天坐标位移序列,多路径提取后的序列如图 5所示。
|
| 图 5 基于CEEMD的多路径提取 |
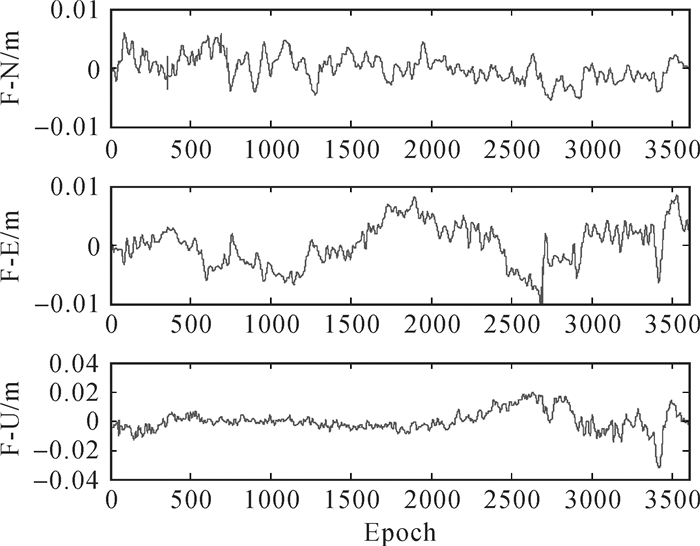
方案4是在方案3的基础上,对CEEMD提取的高频部分和低频部分,分别采用Wavelet和SavGol滤波进行降噪,提取有用信息。Wavelet仍然采用db3小波基函数,进行4层分解。SavGol滤波采用窗口长度为10的5阶多项式拟合平滑。多路径提取后的序列如图 6所示。
|
| 图 6 基于CEEMD-Wavelet-SavGol的多路径提取 |
为了比较4种方案的提取效果,分别从连续两天多路径序列相关系数极大值,以及出现位置、原始序列降噪评价指标方面进行比较,见表 1和表 2。从表 1中可以看出,4种方案连续两天的多路径序列在N、E和U方向相关系数都达到了0.75以上,且极值出现的位置在理论值附近,证明了4种方案的可行性。从表 2可以看出,Wavelet和CEEMD的降噪效果相当,相对于EMD,在相关系数和信噪比及标准差方面较优。新模型相较于CEEMD和Wavelet,在N、E和U方向上,相关系数和信噪比均有提升,标准差分别减小了24.9%、24.4%、19.53%和25.5%、26.58%、21.18%。
| 方案 | N方向 | E方向 | U方向 |
| Wavelet | 0.778 2/-227 s | 0.870 4/-228 s | 0.759 6/-226 s |
| EMD | 0.796 5/-222 s | 0.869 5/-229 s | 0.764 0/-223 s |
| CEEMD | 0.802 2/-226 s | 0.875 1/-229 s | 0.754 5/-229 s |
| 新模型 | 0.825 2/-230 s | 0.882 3/-231 s | 0.772 9/-234 s |
| 方案 | 相关系数 | 信噪比 | 标准差/mm | ||||||||
| N | E | U | N | E | U | N | E | U | |||
| Wavelet | 0.834 9 | 0.885 8 | 0.828 9 | 15.833 9 | 15.919 0 | 12.752 3 | 2.47 | 1.73 | 4.39 | ||
| EMD | 0.820 7 | 0.881 6 | 0.814 3 | 14.864 8 | 15.645 0 | 12.474 0 | 2.58 | 1.76 | 4.45 | ||
| CEEMD | 0.848 2 | 0.887 9 | 0.831 4 | 15.948 3 | 16.086 7 | 12.928 3 | 2.45 | 1.68 | 4.30 | ||
| 新模型 | 0.907 9 | 0.925 7 | 0.865 9 | 18.105 7 | 18.407 8 | 15.263 7 | 1.84 | 1.27 | 3.46 | ||
利用第一天提取的多路径对第二天的原始GPS坐标序列进行修正,修正后坐标序列的标准差见表 3。经过新模型修正后的坐标序列标准差在N、E和U方向分别提高了42.6%、54.0%和37.97%。
| mm | |||
| 方案 | N方向 | E方向 | U方向 |
| 原坐标序列 | 3.64 | 4.11 | 9.27 |
| Wavelet修正后 | 3.54 | 2.76 | 7.37 |
| EMD修正后 | 3.56 | 2.77 | 7.38 |
| CEEMD修正后 | 3.53 | 2.62 | 7.27 |
| 新模型修正后 | 2.09 | 1.89 | 5.75 |
多路径提取是GPS精确定位的一个关键影响因子。利用不同的降噪方法(Wavelet和SavGol滤波),分别对高频信息和低频信息进行处理,提取出坐标序列的多路径,并基于多路径周日重复性,将提取的多路径用于第二天的坐标序列的修正。相比于单一模型,新模型的评价指标值相对较优,多路径的提取效果相对较好,对于GPS信号降噪和精密定位有一定的参考价值。需要指出的是,本文是对解算后坐标序列进行降噪,而对观测值进行多路径的修正来提高定位精度,也是今后的一个研究方向。
| [1] | 戴吾蛟. GPS精密动态变形监测的数据处理理论与方法研究[D]. 长沙: 中南大学, 2007. http://d.wanfangdata.com.cn/Thesis/Y1190458 |
| [2] | 罗飞雪, 戴吾蛟, 唐成盼, 等. 参考经验模态分解-独立分量分析及其在GPS多路径误差处理中的应用[J]. 测绘学报, 2012, 41(3): 366–371. |
| [3] | 于帅, 刘超, 李盟盟, 等. EMD-Wavelet-ICA耦合模型及其在GPS坐标序列降噪中的应用[J]. 测绘科学技术学报, 2016, 33(2): 139–144. |
| [4] | 刘超, 王坚, 胡洪, 等. 动态变形监测多路径实时修正模型研究[J]. 武汉大学学报(信息科学版), 2010, 35(4): 481–490. |
| [5] | 吉绪发, 卢辰龙. GPS多路径误差滤波方法比较研究[J]. 测绘通报, 2015(4): 10–13. |
| [6] | ZHONG P, DING X L, ZHENG D W, et al. Adaptive Wavelet Transform Based on Cross-validation Method and Its Application to GPS Multipath Mitigation[J]. GPS Solutions, 2008, 12(2): 109–117. DOI:10.1007/s10291-007-0071-y |
| [7] | 王婷. EMD算法研究及其在信号去噪中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2010. http://d.wanfangdata.com.cn/Thesis/Y1809491 |
| [8] | 赵志宏, 杨绍普, 申永军. 一种改进的EMD降噪方法[J]. 振动与冲击, 2009, 28(12): 35–37, 62. DOI:10.3969/j.issn.1000-3835.2009.12.010 |
| [9] | TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A Complete Ensemble Empirical Mode Decompo-sition with Adaptive Noise[J]. Brain Research Bulletin, 2011, 125(3): 4144–4147. |
| [10] | 刘爽. 基于CEEMD的地震数据处理研究与应用[D]. 长春: 吉林大学, 2014. |
| [11] | COLOMINAS M A, SCHLOTTHAUER G, TORRES M E. Improved Complete Ensemble EMD.A Suitable Toolfor Biomedical Signal Processing[J]. Biomedical Signal Processing & Control, 2014, 14(14): 19–29. |
| [12] | 位秀雷, 林瑞霖, 刘树勇, 等. 小波和S-G的改进算法及混沌降噪应用[J]. 哈尔滨工程大学学报, 2016, 37(3): 376–381. |
| [13] | 陆化普, 屈闻聪, 孙智源. 基于S-G滤波的交通流故障数据识别与修复算法[J]. 土木工程学报, 2015, 48(5): 123–128. |
| [14] | 甘雨, 隋立芬. 基于经验模态分解的陀螺信号消噪[J]. 测绘学报, 2011, 40(6): 745–750. |
| [15] | 崔冰波, 陈熙源. 基于一种改进EMD算法的GPS多径效应抑制方法[J]. 中国惯性技术学报, 2014, 22(3): 346–351. |
| [16] | 赵迎, 乐友喜, 黄建良, 等. CEEMD与小波变换联合去噪方法研究[J]. 地球物理学进展, 2015, 30(6): 2870–2877. DOI:10.6038/pg20150655 |
| [17] | 戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(4): 321–327. |


