2. 江苏省地理信息资源开发与 利用协同创新中心, 江苏 南京 210023
2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
地理信息事关国家安全,对地理信息的保护十分重要。为维护地理信息安全,国家数据脱密政策法规[1-3]对公开地图的位置精度提出了明确规定,对涉密数据能够达到较好的保密目的,却影响了地理数据的共享使用,造成了数据保密和共享之间的矛盾,脱密技术能够较好地解决该问题。
脱密是指通过技术处理的办法,将秘密级测绘成果中包含的涉及国家安全的地理要素空间位置精度和属性内容进行处理后,转变为符合公开测绘成果使用的方法[4]。地理数据脱密包括几何精度弱化、属性(含注记)和高程处理,以及要素隐藏和伪装等方面。其中,几何精度脱密是指使用脱密技术进行空间位置精度弱化,使得脱密数据不易纠正恢复,避免敏感信息泄露。几何精度脱密是脱密的主要内容。
目前已有的几何精度脱密方法包括投影转换法、图幅变换法、基于移位圆的误差随机干扰法[4]、线性变换法[5, 6]、非线性变换法[7-11]等。这些方法尚存在一些问题:难以高精度恢复的问题;脱密后拓扑关系保持不理想;支持矢栅一体脱密的模型和算法不多;安全性不高;处理速度慢等。本文结合三角函数良好的脱密特性,提出一种基于三角函数的矢栅地理数据可逆脱密模型,为矢栅地理数据的安全保护及共享应用提供有力的技术支持。
1 矢栅地理数据的脱密特征几何脱密实质是对数据进行空间变换处理,矢栅地理数据特征很大程度上影响着其空间变换处理的过程与结果。基于这些特征展开研究,脱密模型和算法才能实现较好的脱密安全性及矢栅数据叠加的空间一致性。
1.1 矢量地理数据的脱密特征矢量地理数据脱密不是简单地变换要素的坐标,其拓扑关系和可用性都对脱密模型和算法提出了更高的要求。结合矢量地理数据特征,对矢量地理数据脱密技术特征进行分析如下:
(1) 较高的数学精度。高精度空间定位特性决定了脱密模型和算法应该满足精确脱密和脱密可逆的要求。算法不仅要有较高的安全性,还要保证脱密数据实现给定的脱密指标。同时,在应用实践中往往要求脱密数据能够高精度恢复到原数据。
(2) 分层的存储方式。矢量地理数据一般分层存储,不同层的数据需要采用相同的脱密模型和算法进行处理,保证它们能够正常叠加显示与使用。
(3) 复杂的数据结构。与栅格地理数据的顺序存储方式不同,矢量地理数据以要素为单元存储离散的坐标点。脱密模型和算法要保证脱密数据的可用性,在改变数据的几何位置精度时,需要控制要素变形,保持拓扑关系不变。
1.2 栅格地理数据的脱密特征栅格地理数据相对于普通栅格图像具有空间地理特征,在脱密模型和算法上,栅格数据具有不同于矢量的特性。栅格地理数据的脱密特征如下:
(1) 空间定位。栅格地理数据是地理空间定位的数据集合,具有空间定位性。因此,栅格地理数据每个像素、所表达的每个实体对象都有空间位置。
(2) 属性精度。相对于一般图像而言,栅格地理数据的属性值具有更高的精度要求,当栅格地理数据作为矢量基础地理数据采集或更新的数据源时,可能涉及模式识别、地物匹配等一系列地图操作。因此,要求脱密算法在重采样的过程中能够保持栅格地理数据的属性精度。
(3) 数据海量。一般的,栅格地理数据量大。栅格地理数据的海量特征对脱密算法的性能要求较高,在保证较强的抗攻击能力的同时,需要降低脱密算法的复杂度,提高海量数据处理的效率。
(4) 分幅存储。栅格地理数据一般是按照图幅组织存储的。脱密模型需要面向分幅的数据,实现空间变换的整体性,脱密后的DOM等栅格地理数据能够较好地拼接使用。
1.3 三角函数脱密适用性分析依据矢栅地理数据脱密特征,提出了脱密模型应满足的指标要求。
(1) 可用性。可用性是指脱密数据能够使用的特性。脱密数据拓扑关系保持良好,要素变形可控。即数据变形光滑连续,地理实体的脱密变换量渐变,无突变。
(2) 可控性。可控性主要体现在两方面:一是脱密的精度可控,能够将数据精确地变换到设定的脱密指标;二是脱密变形可控,满足相邻图幅数据协同处理和数据拼接的需要。
(3) 普适性。国家系列基本比例尺地理数据采用同一脱密模型进行脱密变换,全国范围内采用同一变换模型[13],保证脱密后地理数据在图幅上的连续性;分层存储的矢量地理数据,在相同的数据范围内需采用相同的脱密模型进行处理。
(4) 安全性。安全性是指脱密数据的安全和脱密模型的安全,脱密数据必须满足法律法规对于公开地图的位置精度要求,脱密模型必须具有较强的抗攻击能力,不易破解。
(5) 可逆性。脱密模型不仅能够实现任意精度脱密,还要能够高精度地恢复到原数据。
三角函数是数学函数库中的一类重要函数,它有着优越的函数性质,其周期性、任意阶可导和有界性等特性很好地满足了矢栅地理数据脱密对于变形光滑连续及可控性的需求。作为一种有界函数,其可以通过调整振幅来控制脱密误差分布;作为一种周期函数,它能保证脱密数据在空间上的连续性;作为一种任意阶可导函数,使得脱密效果光滑渐近,保证脱密误差合理分布,维持良好的拓扑关系。因此,三角函数对于矢栅地理数据脱密有着良好的适用性。但是,基本三角函数形式过于简单,容易根据脱密数据反推模型参数,安全性较低。本文基于三角函数提出了矢栅地理数据可逆几何脱密模型,并进行了试验验证。
2 脱密模型的设计与构建 2.1 三角函数模型设计 2.1.1 模型概述傅里叶曾指出任意周期函数都可以表示为不同频率的正弦和或余弦和的形式,多个正弦与余弦和乘以不同的系数,可以表示任意复杂度的周期函数。即基本三角函数的组合能够保持三角函数原有的函数特性。本文采用由正、余弦函数组成的在实数空间内任意阶连续可导的非线性函数模型[14],其图像如图 1所示。

|
| 图 1 三角函数模型图像 |
三角函数模型的表达式如下
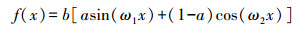 (1)
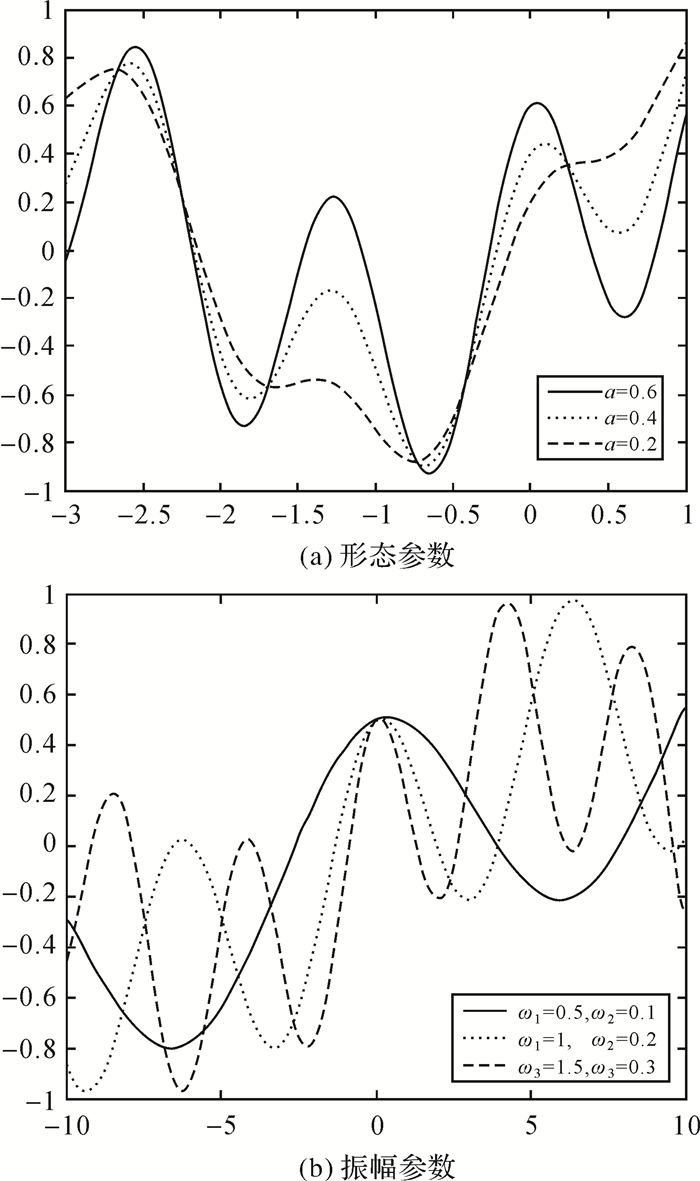
(1) 式中,b表示函数的振幅值;a控制函数的形状;ω1、ω2用于控制函数的周期。在保持其他参数不变的情况下,不同形态参数a的函数图像如图 2(a)所示,不同周期参数ω1、ω2函数图像如图 2(b)所示。
|
| 图 2 不同参数下三角函数模型对比 |
从图 2(a)中可以看出,形态参数越大模型图像抖动越剧烈,如果在模型周期较小的情况下,抖动过于剧烈会使得脱密数据变形较大,影响脱密数据的可用性。因此,需要依据脱密误差,设定适当的形态参数值。对于图 2(b),随着ω1、ω2的增大,模型周期变小。模型的周期T是由正弦函数周期和余弦函数周期两者的最小公倍数决定,模型周期T可以通过式(2)计算得到
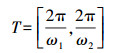 (2)
(2) 式中,[,]表示求两个数的最小公倍数。周期值需要根据数据的图幅范围来恰当选取,如果相对于图幅范围周期过小,将会影响脱密数据的可用性。
2.1.2 三角函数脱密模型式(1)的三角函数模型只对坐标点的y坐标进行变换,x坐标没有改变,使得模型存在漏洞,不宜作为脱密模型。为此,通过对x坐标施加扰动φ来完善模型,建立基于三角函数的脱密模型如式(3)所示。
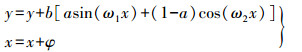 (3)
(3) 同时,式(3)中表示是以x为自变量y方向的三角函数变换,也可实现以y为自变量x方向的三角函数变换,如下
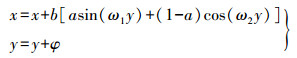 (4)
(4) 在实际应用中,可以选择式(3)或式(4)作为脱密模型进行脱密处理。
2.1.3 三角函数恢复模型三角函数模型只与模型的5个参数a、b、ω1、ω2、φ有关,脱密处理只是在原数据的x坐标或y坐标上施加的一个增量,而恢复处理只需将脱密数据的x坐标或y坐标上施加的增量减去,增量与减量根据式(1)计算得到,在参数相同的情况下,增量和减量的值是相同的,不存在精度损失。故由三角函数脱密模型可得恢复模型如下
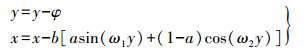 (5)
(5) 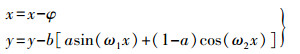 (6)
(6) 式(5)是x方向恢复,式(6)是y方向恢复。
2.2 脱密误差控制算法几何脱密以中误差作为精度指标,误差控制算法是通过迭代模型参数的方式控制中误差的缩放[12],使得脱密数据达到设定的脱密指标。算法流程如图 3所示。
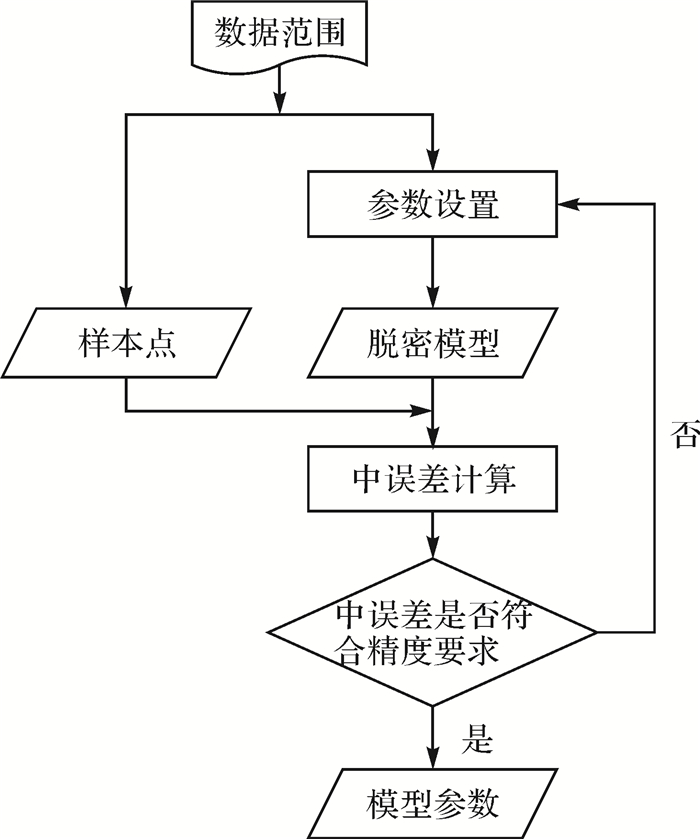
|
| 图 3 误差控制算法流程 |
其中,中误差RMS实际上是脱密误差分布的均方根误差,其计算公式如下
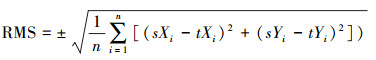 (7)
(7) 式中,RMS为中误差值;n是样本点的个数;(sXi, sYi)是源坐标;(tXi, tYi)是脱密后坐标。
误差控制算法的核心是迭代参数的确定,迭代参数可以在模型的可变参数中选择。三角函数的可变参数包括形态参数a、周期参数ω1和ω2、振幅参数b和偏移量φ。其中,形态参数a对于脱密误差的影响较小,对于数据可用性影响明显;模型的周期与数据范围关系紧密,需要以安全可用为前提设置合理的周期参数ω1和ω2,该参数对中误差影响很小,调节误差的能力有限,故不作为误差控制的迭代变量。偏移量φ用于弥补非变换方向无位移的缺陷,以式(3)所示模型为例,脱密中误差RMS的计算公式如下
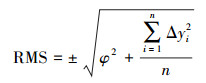 (8)
(8) 式中,n是样本点的个数;Δyi是样本点y方向的变换量。由式(8)可看出偏移量φ属于系统误差,对数据没有非线性变形影响,将其作为迭代参数达不到脱密误差均匀分布的要求,故不可作为迭代参数,但它作为脱密中误差的一部分可以根据式(9)求得
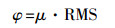 (9)
(9) 式中,μ∈[0, 1]。
振幅参数在形态参数和周期参数不变的前提下,可以作为迭代参数控制脱密中误差主要组成部分。振幅越大,脱密中误差越大;振幅越小,脱密中误差越小。因此,三角函数脱密模型以振幅参数作为迭代算子进行误差控制。
2.3 矢栅地理数据脱密模型构建根据原始矢栅地理数据求解三角函数脱密模型,采用三角函数脱密模型对矢栅地理数据进行脱密处理。脱密模型的构建流程如图 4所示。
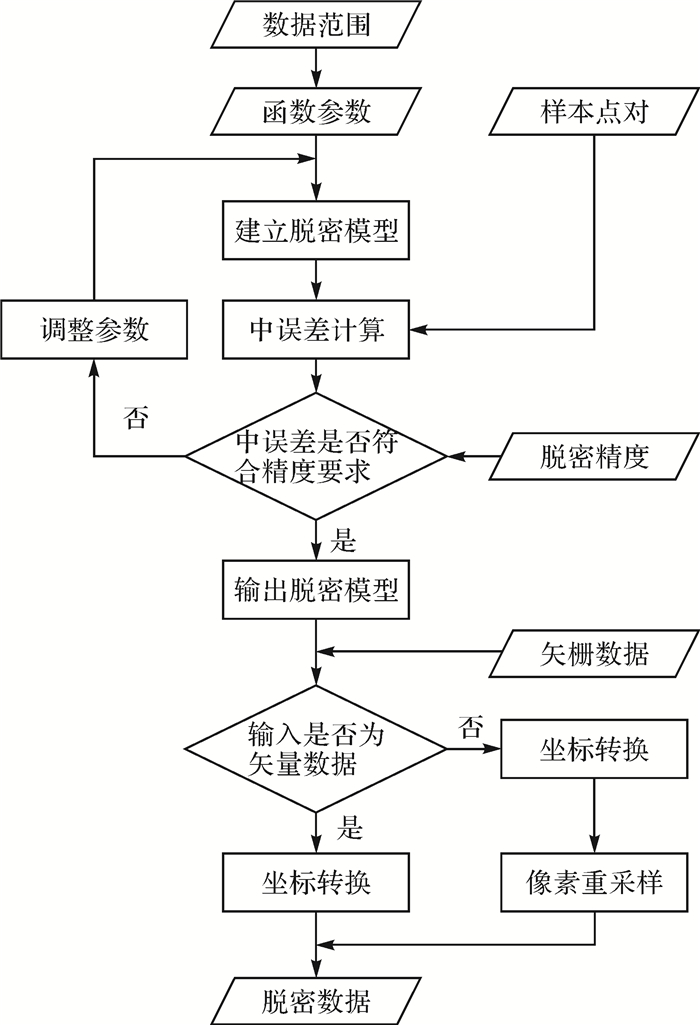
|
| 图 4 矢栅地理数据脱密流程 |
脱密模型构建的具体步骤如下:
(1) 确定数据范围。输入具有相同空间参考的矢量地理数据和栅格地理数据,获取数据范围。
(2) 解算模型参数。在保证三角函数图像均匀变化的条件下,设定形态参数a。根据数据范围或用户输入的周期T,按照式(10)计算周期参数ω1、ω2。
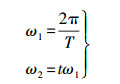 (10)
(10) 式中,t用于控制三角函数图像形状,本文设定t=0.5。
根据式(11)求取振幅参数的初始值,并将计算得到的5个参数代入式(11)中建立三角函数脱密模型。
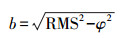 (11)
(11) (3) 样本点选择。以数据范围作为全局样本,取x方向的宽度为xlength,y方向的宽度为ylength,设定间隔为interval,在全局样本中均匀地选取num=(xlength/interval)·(ylength/interval)个点作为计算全图中误差的样本点。
(4) 中误差的迭代控制。用步骤(2)建立的脱密模型对样本点ps(ssXi, ssYi)(i=1, 2, …, num)作脱密处理,得到脱密后的样本点坐标Ts(tsXi, tsYi)(i=1, 2, …, num)。由式(7)计算样本点中误差RMSdecrypt,将RMSdecrypt与脱密指标d进行比较。如果RMSdecrypt < d,则根据式(12)增大b来增大全图中误差; 如果RMSdecrypt>d,则根据式(12)缩小b来减小全图的中误差。
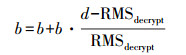 (12)
(12) 迭代步骤(2)到步骤(4),中误差达到脱密指标后执行步骤(5)。
(5) 矢栅地理数据脱密处理。采用步骤(4)输出的三角函数脱密模型对矢栅地理数据进行脱密处理,矢量地理数据对坐标点集进行坐标变换,栅格地理数据对像素点的坐标进行变换,之后,对像素点进行重采样,将脱密的矢栅地理数据叠加输出。
2.4 矢栅地理数据恢复模型构建矢栅地理数据恢复模型与脱密模型的流程类似,都是解算三角函数恢复模型的参数,并采用恢复模型处理矢栅地理数据。恢复模型构建的具体步骤如下:
(1) 恢复模型的建立。将前文步骤(4)输出的三角函数脱密模型的5个参数a、ω1、ω2、b、φ代入式(5)或式(6)中,建立恢复模型。
(2) 矢栅地理数据恢复处理。采用步骤(1)输出的恢复模型处理矢栅地理数据,矢量地理数据对坐标点集进行坐标变换,栅格地理数据对像素点的坐标进行变换之后,对像素点进行重采样,将恢复后的矢栅地理数据叠加输出。
3 试验分析本文采用某地相同区域TIF格式的栅格地理数据和SHP格式的湖泊、居民地和河流3种矢量地理数据作为试验数据,其坐标系统为WGS-84高斯投影坐标系,比例尺为1:2000。栅格数据的分辨率为0.2 m,数据尺寸为3667×3475像素。试验数据如图 5所示。

|
| 图 5 试验原始数据 |
采用试验数据进行三角函数脱密试验,模型的目标脱密精度为50 m。在数据范围中均匀选取255个样本点,根据前文流程计算三角函数脱密模型的5个参数,建立三角函数脱密模型,得到模型参数a=0.5, b=21.810 6, ω1=0.062 831 8, ω2=0.012 566 4, φ=48.587。3种矢量地理数据的脱密叠加效果如图 6所示,粗线部分是脱密前数据,细线部分为脱密数据;栅格地理数据的脱密效果如图 7所示,(a)表示脱密前数据,(b)表示脱密数据。
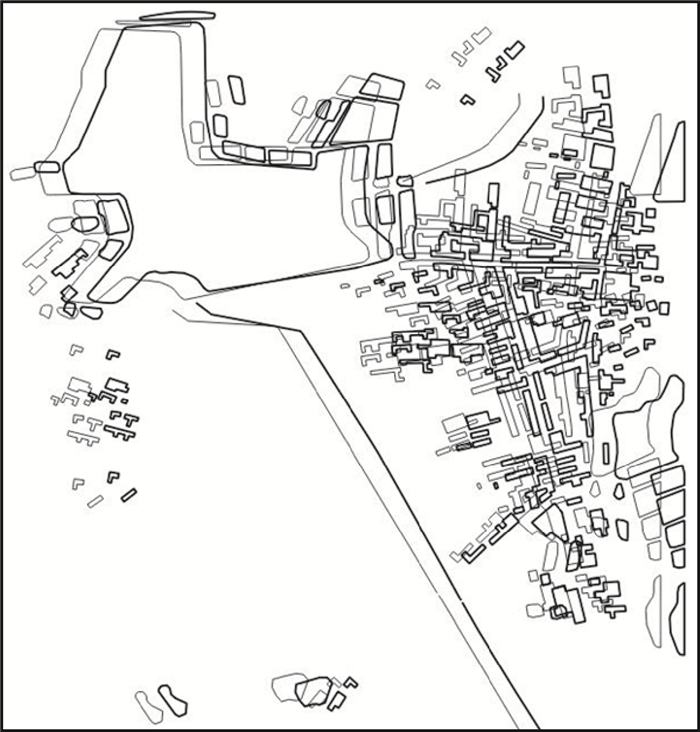
|
| 图 6 三角函数模型矢量地理数据脱密效果 |

|
| 图 7 栅格地理数据脱密效果 |
从图 6可以看出脱密后要素之间的拓扑关系保持较好,并且要素的几何形状并没有发生突变。其中,对河流、湖泊和居民地3种矢量地理数据采用同一种脱密模型进行脱密处理,可以看出3个矢量图层叠加后,要素之间的拓扑关系保持良好。
将脱密后矢栅地理数据叠加输出,并与脱密前数据叠加效果作对比,如图 8所示,(a)表示脱密前矢栅地理数据叠加效果,(b)表示脱密后矢栅地理数据的叠加效果。

|
| 图 8 矢栅地理数据叠加效果 |
从图 8(b)可以看出居民地、河流和湖泊要素叠加效果较好。
4 结语本文分析了矢栅地理数据的脱密特征,提出了脱密指标要求,结合三角函数良好的脱密数学特征,基于正、余弦函数,提出并构建了一体化的非线性矢栅地理数据可逆几何脱密模型,并进行了试验验证。结果表明,该模型具有安全可靠、可逆可控、拓扑关系保持、矢栅一体、数据脱密处理效率高等特点。
| [1] | 国家测绘地理信息局. 测绘管理工作国家秘密范围的规定[EB/OL]. 2003-12-23(2014-02-21). http://www.sbsm.gov.cn. |
| [2] | 国家测绘地理信息局. 公开图内容表示补充规定(试行)[EB/OL]. 2009-01-23. www.sbsm.gov.cn/artical/zcfg/zygfxwj/201009/2010090007392. shtml. |
| [3] | 国家测绘地理信息局. 基础地理信息公开表示内容的规定(试行)[EB/OL]. 2010-09-17. www.sbsm.gov.cn/article/zcfg/zygfxwj/201211/20121100116440. shtml. |
| [4] | 傅宏. 公众版地图地理要素脱密处理方法[J]. 地理空间信息, 2010, 8(4): 133–134. |
| [5] | 郭金运, 朱明法, 徐泮林. 地图数据几何纠正时仿射变换与相似变换的对比分析[J]. 测绘通报, 2001(4): 23–24, 27. |
| [6] | 秦李颗. 互联网环境下地理空间数据的保密技术研究[D]. 西安: 长安大学, 2007. |
| [7] | WANG P, QU Z G, WANG P, et al. A Coarse-to-fine Matching Algorithm for FLIR and Optical Satellite Image Registration[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 599–603. DOI:10.1109/LGRS.2011.2176102 |
| [8] | ROCCHINI D, DI RITA A. Relief Effects on Aerial Photos Geometric Correction[J]. Applied Geography, 2005, 25(2): 159–168. DOI:10.1016/j.apgeog.2005.03.002 |
| [9] | SU Q, CHENG H, SUN W, et al. A Novel Correction Algorithm Based on Polynomial and TPS Models[C]//Proceedings of the 2011 International Conference on Information Technology, Computer Engineering and Management Sciences (ICM).[S.l.]:IEEE, 2011:52-55. |
| [10] | WANG C, ZHANG Y, LIU P, et al. A Self-adjustive Geometric Correction Method for Seriously Oblique Aero Image[C]//Proceedings of the 2011 IEEE Geoscience and Remote Sensing Symposium(IGARSS), International.[S.l.]:IEEE, 2011:1433-1436. |
| [11] | GILLMAN D.Triangulations for Rubber Sheeting[C]//Proceedings of 7th International Sym posium on Computer Assisted Cartography (AutoCarto 7). Washington D.C.:[s.n.], 1985. |
| [12] | 闫娜. DOM几何精度脱密模型与算法研究[D]. 南京: 南京师范大学, 2013. |
| [13] | 李成名, 刘勇, 王继周, 等. 移动GIS及其在国土资源信息化中的应用[J]. 国土资源信息化, 2002(6): 33–36. |
| [14] | 徐耀群, 何少平. 三角函数自反馈混沌神经网络及其应用[C]//2009中国控制与决策会议论文集. 桂林: [s. n. ], 2009. |



