网络RTK技术是目前实现高精度定位的重要手段之一,其关键问题是基准站间整周模糊度的准确解算,只有准确地确定了基准站间的整周模糊度,才能建立高精度的误差模型,进而实现流动站整周模糊度的固定和得到高精度的定位结果。网络RTK基准站间的距离一般达到50 km左右,电离层延迟和对流层延迟等误差对双差观测值的影响远远大于0.5周,因此采用简单的差分算法很难准确固定基准站间的整周模糊度[1]。目前,国内外学者对网络RTK基准站间模糊度的解算进行了大量研究并取得了初步成果,文献[1]和文献[2]提出了中距离网络RTK模糊度解算方法[2];文献[3]提出了模糊度的单历元解算方法[3],文献[4]和文献[5]提出对流层延迟的误差解算模型,提高了模糊度浮点解的精度,但是目前已有的这些网络RTK基准站间模糊度的解算方法站间距只能达到80 km;而大范围的网络RTK基准站间的距离达到150 km左右[2, 4-5],现有的网络RTK基准站间模糊度的解算方法很难准确快速地固定模糊度,因此本文提出一种大范围网络RTK基准站间整周模糊度的解算方法,首先利用L1、L2载波相位观测值和P1、P2伪距观测值解算基准站间的双差宽巷模糊度,然后与无电离层组合观测方程联立消除电离层延迟误差,采用Saastamoinen模型和Chao映射函数模型相结合的方法解算双差对流层延迟误差,最终确定L1、L2双差载波相位整周模糊度。
1 观测方程 1.1 双差观测方程载波相位双差观测方程不仅消除了接收机钟差和卫星钟差,而且大大削弱了电离层延迟误差、对流层延迟误差、卫星轨道误差等误差的影响[6],因此本文采用双差观测值解算基准站载波相位整周模糊度。伪距和载波相位双差观测方程分别为
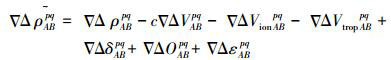 (1)
(1) 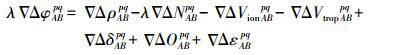 (2)
(2) 式(1)和式(2)中,▽△表示双差算子;A、B表示测站;p、q表示卫星号;
在双差观测方程中,基准站坐标被视为已知值,因此基准站方向余弦值为零[7],因此双差观测方程线性化后的形式分别为
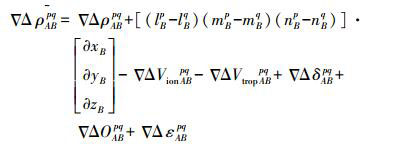 (3)
(3) 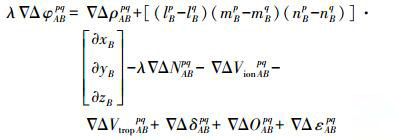 (4)
(4) 式中
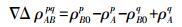 (5)
(5) 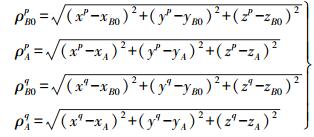 (6)
(6)  (7)
(7) 在解算大范围网络RTK基准站间整周模糊度的过程中,随着基准站间距离的增大,对流层延迟误差、电离层延迟误差和卫星轨道误差残差严重影响载波相位整周模糊度的固定,因此,本文采用不受电离层延迟误差、对流层延迟误差、卫星轨道误差和几何距离影响的MW组合观测值解算双差宽巷模糊度[8],即
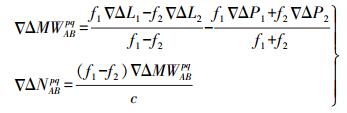 (8)
(8) 式中,f1、f2为载波L1、L2的频率;▽△L1、▽△L2为以距离为单位的L1、L2双差观测值;▽△P1、▽△P2为伪距P1、P2的双差观测值;▽△MWABpq为MW组合观测值;▽△NABpq为宽巷双差整周模糊度。
因为MW组合观测值消除了电离层延迟误差、对流层延迟误差和卫星轨道误差等误差的影响,只受观测噪声的影响,所以可以通过多个历元的平均值来求解双差宽巷整周模糊度。为了保证解算出的双差宽巷整周模糊度的正确性,需要对解算出的双差宽巷整周模糊度进行验证,以保证双差宽巷整周模糊度的准确固定[9-10]。利用3个基准站组成的闭合基线双差宽巷整周模糊度之和为零来验证,即
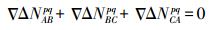 (9)
(9) 在宽巷双差整周模糊度准确固定后,为了保证载波相位整周模糊度的准确固定,需要对各项误差进行处理。本文采用的是广播星历数据进行解算,对于200 km长度以下的基线而言,卫星轨道误差可以忽略不计,电离层延迟误差可以通过无电离层组合观测值消除,而基准站一般设在比较开阔的地方,这在一定程度上削弱了多路径效应的影响,除对流层延迟以外的其他误差通过双差观测值处理以后的残差可以忽略不计,因此只需要着重处理对流层延迟的误差。
首先,采用Saastamoinen模型[11-13]计算天顶对流层的干、湿延迟分量,公式为
天顶干延迟分量
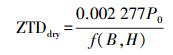 (10)
(10) 天顶湿延迟分量
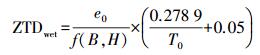 (11)
(11) 式中,标准大气压P0=1 013.25 mbar;标准水汽压e0=11.691 mbar;标准绝对温度T0=288.15 K;f(B, H)是与基准站大地坐标相关的函数,可表示为
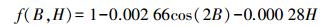 (12)
(12) 式中,(B, H)表示测站的大地坐标纬度和高程。选择Chao映射函数模型[14-15]作为解算对流层延迟的映射函数,如式(13)所示。最后,根据式(14)解算双差对流层延迟误差。
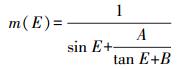 (13)
(13) 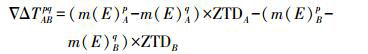 (14)
(14) 对于干分量的映射函数, 式(13)中的常数A=0.001 433,B=0.044 5;对于湿分量映射函数,式(13)中的常数A=0.000 35,B=0.017。式(14)中,▽△为双差算子;T为对流层延迟;A、B为基准站;p、q为卫星号;ZTDA、ZTDB分别为基准站A、B的天顶对流层延迟。
2.3 双差载波相位模糊度解算通过误差处理后,基准站A、B对卫星p、q的载波相位双差观测方程可表示为
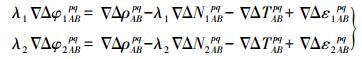 (15)
(15) 式中,1表示频率L1;2表示频率L2;λ为波长;▽△为双差算子;ρ为卫星到测站的距离;N为载波相位整周模糊度;T为对流层延迟;ε为测量噪声。
由式(15)可得到双差无电离层组合载波相位观测方程为
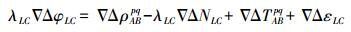 (16)
(16) 式中,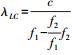
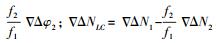
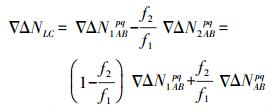 (17)
(17) 将式(17)代入式(16)双差无电离层组合载波相位观测方程可得
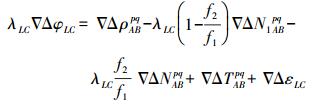 (18)
(18) 因此,利用式(18)即可实现L1载波相位双差整周模糊度的解算,而L2载波相位双差整周模糊度可以表示为
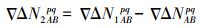 (19)
(19) 为了保证解算出的载波相位双差整周模糊度的正确性,需要对解算出的载波相位双差整周模糊度进行验证,以保证解算出的载波相位双差整周模糊度的可靠性。利用3个基准站组成的闭合基线载波相位双差整周模糊度之和为零来验证,即
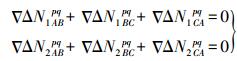 (20)
(20) 如果解算出的L1、L2载波相位双差整周模糊度满足式(20),则认为解算出的载波相位双差整周模糊度是正确的。
3 试验分析为了验证本文算法的正确性,采用CORS站的实测数据进行检验,采用2014年10月9日采集的CORS站数据进行大范围网络RTK基准站间模糊度的解算,卫星截止高度角设置为15°,数据采样率为15 Hz。
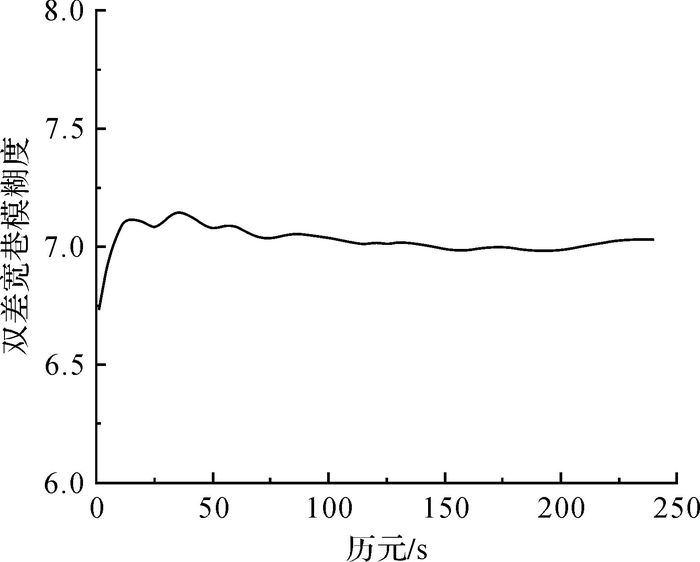
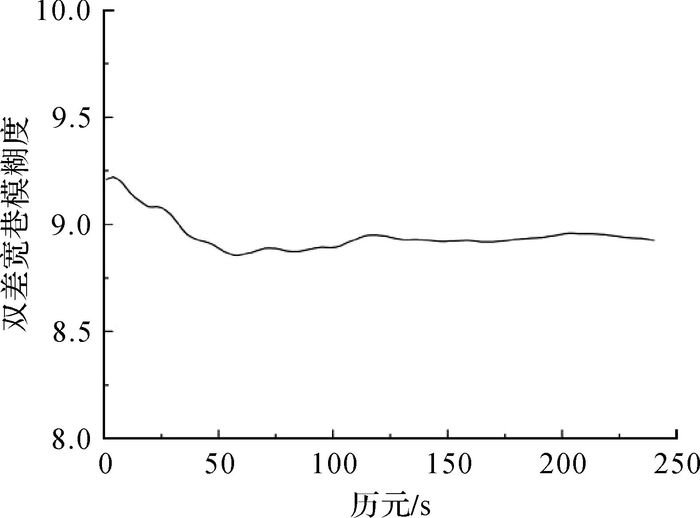
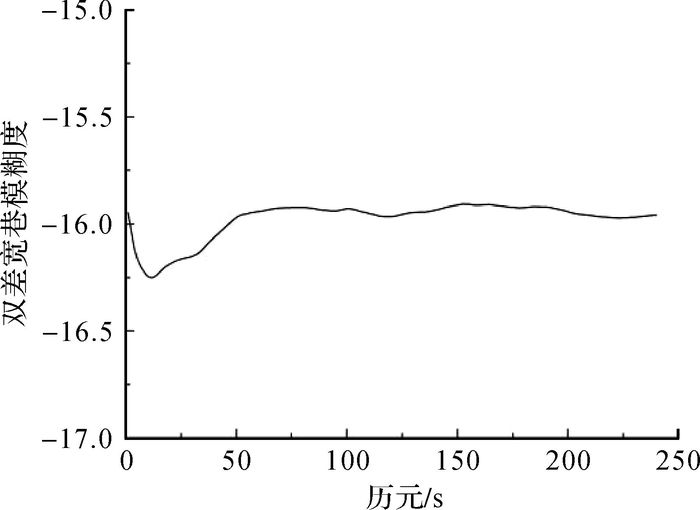
首先利用本文提出的基准站间双差宽巷整周模糊度的解算方法解算基准站间的双差宽巷整周模糊度,同时将本文的解算结果与GAMIT软件解算结果进行比较,这里以16号卫星为基准卫星,23号卫星的解算结果为例,GAMIT软件的解算结果见表 1,3条基线的双差宽巷模糊度的解算结果如图 1—图 3所示。
|
| 图 1 基线Base1—Base2双差宽巷模糊度 |
|
| 图 2 基线Base2—Base3双差宽巷模糊度 |
|
| 图 3 基线Base3—Base1双差宽巷模糊度 |
从图 1—图 3中可以看出,双差宽巷模糊度的浮点解只需要大约2 min的时间即可收敛,然后趋于稳定,因为本文采用多个历元求平均值的算法减少了观测噪声的影响,使双差宽巷模糊度计算值越来越稳定,3条基线的双差宽巷模糊度依次收敛于7、9和-16,与表 1中GAMIT软件的解算结果相同,同时满足双差宽巷模糊度的检核条件(式(19)),证明该算法可以准确快速地解算大范围网络RTK基准站间双差宽巷整周模糊度。
在正确解算出基准站间双差整周模糊度以后,采用Saastamoinen模型和Chao映射函数模型相结合的方法解算双差对流层延迟误差,然后根据式(18)解算双差载波相位整周模糊度,这里只给出L1双差载波相位模糊度解算结果,L2载波结果与L1载波类似。结果如图 4—图 6所示,同时将本文的解算结果与表 2中的GAMIT软件的解算结果进行比较,这里仍以16号卫星为基准卫星,23号卫星的解算结果为例。
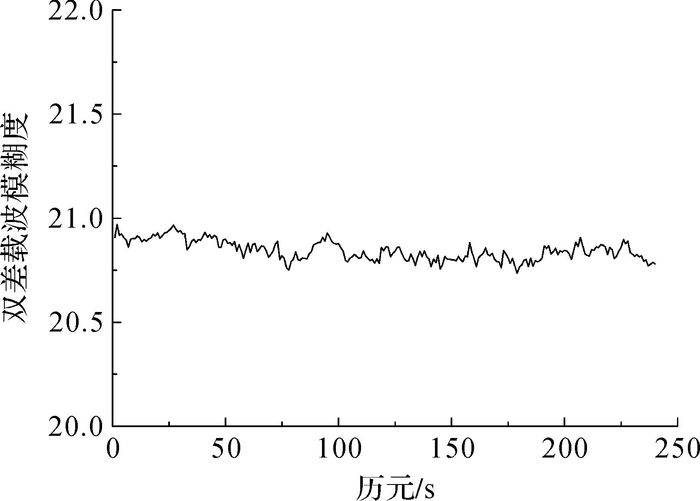
|
| 图 4 基线Base1—Base2双差载波模糊度 |
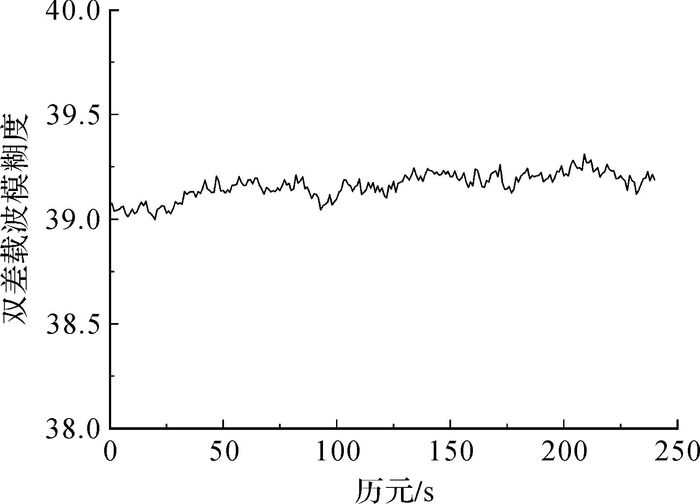
|
| 图 5 基线Base2—Base3双差载波模糊度 |
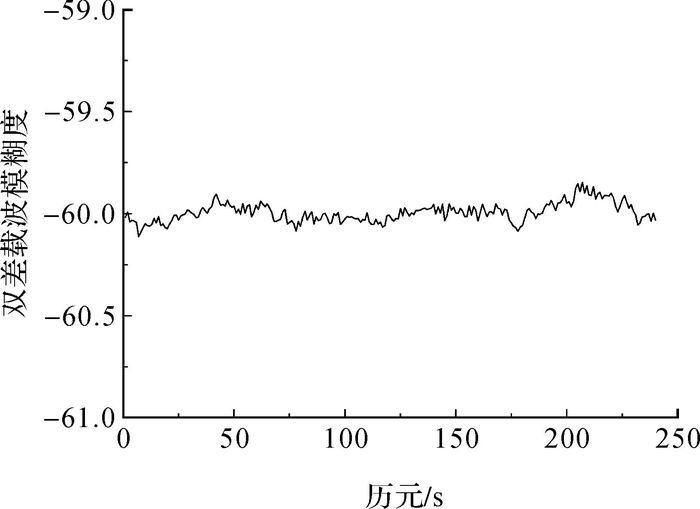
|
| 图 6 基线Base3—Base1双差载波模糊度 |
从图 4—图 6中可以看出,双差载波相位模糊度的浮点解单历元即可收敛,3条基线的双差载波相位模糊度依次收敛于21、39和-60,与表 2中GAMIT软件的解算结果相同,同时满足双差载波相位模糊度的检核条件(式(20)),证明该算法可以准确快速地解算大范围网络RTK基准站间双差载波相位整周模糊度。
4 结语本文首先采用L1、L2载波相位观测值和P1、P2伪距观测值组成的MW组合观测值解算基准站间的双差宽巷模糊度,然后与无电离层组合观测方程联立消除电离层延迟误差,采用Saastamoinen模型和Chao映射函数模型相结合的方法解算双差对流层延迟误差,最终确定L1、L2双差载波相位整周模糊度。经CORS网实测数据实验算例的验证,该方法可以实现大范围网络RTK基准站间的载波相位整周模糊度的实时快速准确解算,同时,用Saastamoinen模型和Chao映射函数模型相结合的方法解算双差对流层延迟误差在达到同样精度的情况下模型简便,计算量小,提高了载波相位整周模糊度的解算效率,实现了双差载波相位整周模糊度的单历元固定。
| [1] | 祝会忠, 徐爱功, 高猛, 等. BDS网络RTK中距离参考站整周模糊度单历元解算方法[J]. 测绘学报, 2016, 45(1): 50–57. |
| [2] | 王珍. 网络RTK动态中长基线模糊度解算方法比较研究[J]. 测绘与空间地理信息, 2016, 39(2): 71–74. |
| [3] | 刘会, 郑衍宁, 徐琪尧, 等. 一种GPS单历元整周模糊度固定方法[J]. 导航定位学报, 2016, 4(2): 57–61. |
| [4] | 祝会忠, 徐爱功, 高猛, 等. 长距离网络实时动态对流层延迟误差改正[J]. 测绘科学, 2015, 40(6): 30–35. |
| [5] | 王建敏, 黄佳鹏, 祝会忠, 等. 电离层总电子数预报方法研究[J]. 测绘科学, 2016, 41(12): 47–52. |
| [6] | 吕伟才, 高井祥, 张书毕, 等. 宽巷约束的网络RTK基准站间模糊度固定方法[J]. 中国矿业大学学报, 2014, 43(5): 933–937. |
| [7] | 李磊, 徐爱功, 祝会忠, 等. 长距离网络RTK基准站间整周模糊度的快速解算[J]. 测绘科学, 2014, 39(10): 22–25. |
| [8] | 祝会忠, 刘经南, 唐卫明, 等. 长距离网络RTK基准站间整周模糊度单历元确定方法[J]. 测绘学报, 2012, 41(3): 359–365. |
| [9] | 柯福阳, 王庆, 潘树国. 网络RTK长基线模糊度解算方法研究[J]. 大地测量与地球动力学, 2012, 32(5): 72–77. |
| [10] | 王建敏, 马天明, 祝会忠. 改进LAMBDA算法实现BDS双频整周模糊度快速解算[J]. 系统工程理论与实践, 2017, 37(3): 768–772. DOI:10.12011/1000-6788(2017)03-0768-05 |
| [11] | SAASTAMOINEN J. Contributions to Theory of Atmospheric Refraction[J]. Journal of Geodesy, 1972, 105(1): 279–298. |
| [12] | SAASTAMOINEN J. Introduction to Practical Computation of Astronomical Refraction[J]. Journal of Geodesy, 1972, 106(1): 383–397. |
| [13] | SAASTAMOINEN J. Contributions to the Theory of Atmospheric Refraction Part Ⅱ:Refraction Corrections in Satellite Geodesy[J]. Journal of Geodesy, 1973, 107(10): 13–34. |
| [14] | 赵铁成, 韩曜旭. GPS定位系统中几种对流层模型的探讨[J]. 全球定位系统, 2011, 36(1): 46–52. |
| [15] | 王鹏旭, 吕志伟, 杨东森, 等. 一种新的中长基线BDS三频模糊度快速解算方法[J]. 测绘通报, 2017(4): 25–29. |
| [16] | 王建敏, 马天明, 祝会忠. BDS/GPS整周模糊度实时快速解算[J]. 中国矿业大学学报, 2017, 46(3): 672–678. |
| [17] | 谢建涛, 郝金明, 于合理, 等. 基于BDS+GPS中长基线多频RTK定位的快速收敛模型[J]. 测绘通报, 2016(5): 6–10, 17. |



