在计算机制图的时代,GIS软件的功能日益强大,应用更加广泛。在对河流进行分级时,不必像过去一样对每一条河段进行选取、查看,而是依赖自动成图的手段,通过河段的属性、几何特征等信息对河流进行自动分级。相较于人工指定河流等级,自动分级不仅减轻了人工烦琐的劳动,也提高了河流分级的精确度。
目前对河流进行自动分级的研究有:毋河海[1]建立了河流树对进行分级,并认为河流中主流具有最大的长度,可以通过寻找最大长度的河流来确定主流,但仅用河流的长度来确定主流时,分级的结果不顾及河流的流向和特征,只追求最长,导致分级不准确;Paiva[2]等针对河流中各条河段流向的地质知识,即在河流的汇合处, 上下游河段的流向几乎在一条直线上,提出了一种用角度判别等级的方法, 但仅用角度进行分级时,若在河段的节点处出现角度偏差,分级结果也会出现较大偏差;郭庆胜[3]等认为,主流往往是最长的河流,在节点处也符合180°假设,将两种方法结合起来对河流进行主支流的判断,通过长度角度来综合考虑河流等级,但未考虑河流的属性信息和河流的实际意义;吴伟[4]等在对河流进行渐变时,运用了流向、图层、名称等的属性信息进行约束,加强了河流分级的合理性,但仅用角度进行分级会出现一些分级错误。以上的研究工作中,均未对河系中的环进行处理,且在求取河流的最长路径时效率较低。
综上,本文运用属性和几何规则对河系进行了分级,依据河系中不同的环类型分为单入单出环和多入多出环;并对不同类型的环运用最短路径和角度优先的方法进行了处理;同时,对于几何规则判断中最长路径搜索效率较低的问题,采用了启发式的算法,减少了搜索的次数,从而提高了效率。
1 河流分级规则在已有的研究成果中,河流分级的基本方法可总结如下[5-9]:
首先,对河系信息进行重新组织,构建河流树,以河流的一个汇出点作为起始节点来进行河流的搜索,寻找主流,并将主流作为河流的第一级;将该主流从河系中去除,从主流中存在支流的节点继续搜索,寻找主流,作为河流的第二级;递归调用对河流进行搜索,依次向下分级,直到河流的所有河段都被搜索过为止。
在搜索的过程中,如何准确地确定主流至关重要,决定了最终的河流分级结果[10-11]。对河流主流的判断采用属性信息和几何特征相结合的方式。其中,河流的属性包括:河流的名称、河流的类型、河流的流向等;几何特征包括:河流的角度、河流的长度、河流是否有环等。本文据此提出河流分级的规则如下:
1.1 属性信息规则运用河流的属性特征建立一些规则来确定主流,这些信息可以从河流的属性信息中读取和判断,规则如下(优先级自上而下):
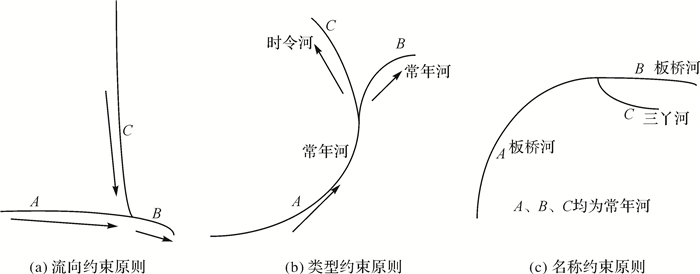
(1) 河流流向约束原则,即流向与当前河流不一致的河流不能构成同一河流。
(2) 河流类型约束原则,即相同的河流类型优先构成同一河流。
(3) 河流名称约束原则,即相同的河流名称优先构成同一河流。
如图 1所示,当前河流均是A河流,分别依据上述原则,选择B为下一条主流。
|
| 图 1 主流选择示意图 |
若河流无属性信息或属性信息不足以确定哪一个候选河段为主流时,就需要以河流的形状特征来判断。河流的几何特征主要是河流的角度、长度。河流的角度是判断当前河段与下一河段的角度,优先选择平直的河段;而河流的长度则是判断下一河段是否在从当前河段出发的最长路径上,优先选择在最长路径上的河段。规则如下(优先级自上而下):
(1) 长度优先原则,若该河段出发的最长路径远远大于其他路径,则选择最长路径上的河段优先构成同一河流。如图 2所示,应用该原则选择路径长的作为河流的主流。

|
| 图 2 长度优先原则 |
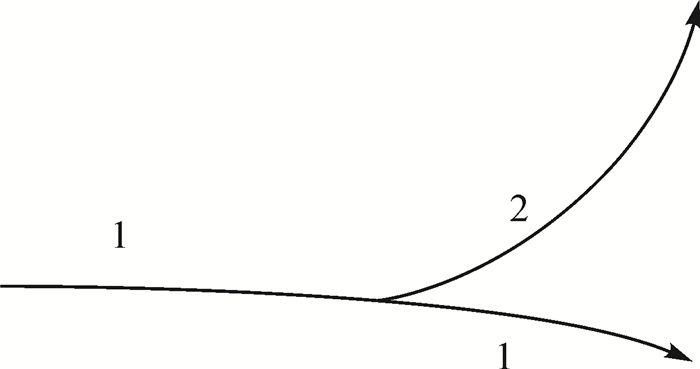
(2) 角度优先原则,若从该河段出发的最长路径与候选河段的长度相近,且候选河段的角度比最长路径上的角度好很多,则应选择角度好的候选河段作为主流。如图 3所示,应用该原则选择角度较好的作为河流主流。
|
| 图 3 角度优先原则 |
上述基本原则可以对无环的河流进行分级,但当河流中出现环时,上述规则对河流的分级效果欠佳。因此,本文对环进行了详细的分类,以选择不同的方法对河流环进行处理。
1.3.1 单入单出环河流中的单入单出环是指只有一个入口和一个出口的环。单入单出环在河流分级中最为常见,由于环的凸起部分路径往往较平直的路径长,运用上述原则对环进行判断时,一般选择长度较长的那条路径,会造成分级的错误。因此,需要对河流中的单入单出环作判断。在找出单入单出环后,选择从环的入口到出口之间的路径最短的或与入口处的弧段所成的角度较好的那条路径作为主流,可以大大减少单入单出环的分级错误。如图 4所示的单入单出环,选择了长度较短路径的作为河流的主流。

|
| 图 4 河流中单入单出环 |
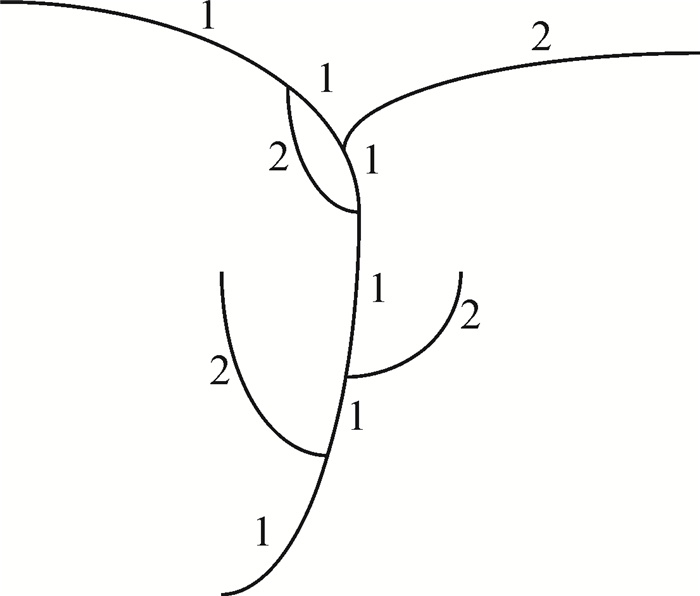
多入多出环则是河流环有多个入口或多个出口,环中的河流流向多条河流,如图 5所示。这时,可以遵照角度优先的原则,即选择入口河段与环的两条路径中所成角度最好的作为主流,这样就可避免大多数多入多出环的分级错误。如图 5所示的多入多出环,选择角度较好的作为河流的主流。
|
| 图 5 河流中多入多出环 |
河流的自动分级首先需要对河系构建河系树,寻找河流的一个汇出点作为起始节点来搜索;再通过主流识别,确定该条主流的等级;最后进行迭代处理,从而对每一条河流进行分级。主流识别需要利用河流的属性信息和几何特征,根据上文所述的规则进行判断。在分级的过程中,属性信息优先级大于几何特征优先级,即先通过属性信息判断等级,在无属性信息或属性信息不足以分级的情况下,再用几何信息进行分级。
|
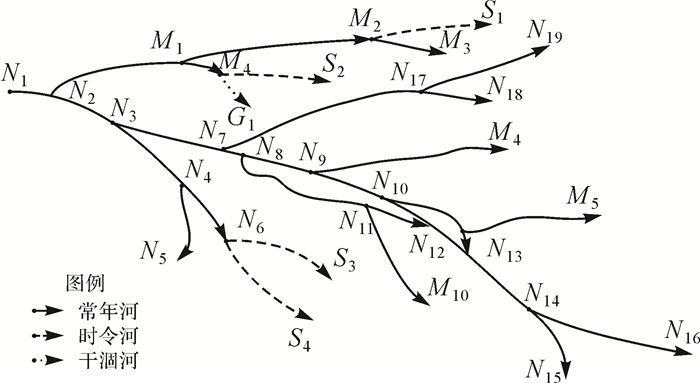
| 图 6 河系图 |
| 河段编号 | 河流类型 | 河流名称 |
| (N1,N2),(N2,N3),(N3,N4),(N4,N5),(N,N6),(N3,N7),(N7,N8),(N8,N9),(N9,N10),(N10,N12),(N8,N11),(N11,N12),(N10,N13),(N12,N13),(N13,N14),(N14,N15),(N14,N16) | 常年河 | 板桥河 |
| (N7,N17),(N17,N18),(N17,N19) | 常年河 | 三丫河 |
| (N2,M1),(M1,M4),(M1,M2),(M2,M3),(N9,M4),(N13,M5),(N11,M10) | 常年河 | — |
| (M2,S1),(M4,S2),(N6,S3),(N6,S4) | 时令河 | — |
| (M4,G1) | 干涸河 | — |
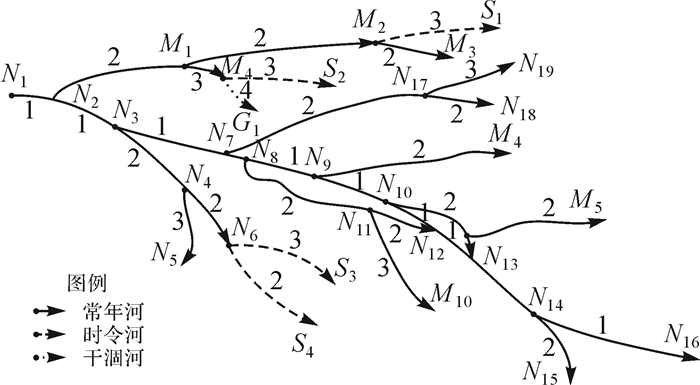
根据上文所述的属性信息规则,可以运用属性信息对河流的主流进行判断。如图 6所示,在M2处,由于(M2,S1)为时令河,与上一个河段的河流类型不同,因此选择(M2,M3)为主流。又如在N2处,选择下一条主流河段,由于两条候选河段与(N1,N2)的类型都相同,因此用名称信息来判断主流。由于(N2,M1)的河段名称与(N1,N2)河段不同,而与(N2,N3)的名称相同,因此选择(N2,N3)作为主流河段。在N3节点处,(N3,N7)与(N3,N4)为两条候选河段,两个河段的类型和名称均相同,因此需要用几何特征来选择主流河段。
2.2 几何特征确定主流在几何规则中,采用长度结合角度判断主流的方式对主流进行判别。利用长度判别时,需要寻找河流的最长路径,这可认为是对有向图进行单源最长路径的搜索问题。对河系树的最长路径问题[12]描述如下:
设G=(V, A)是一个完全连通图,V={0, 1, …, n}节点集合,(Xn, Yn)是节点n的地理坐标,A={(i, j), i, j∈V}是弧集合。其中, 0节点是起始节点, 最长路径的求解目标是找到一条从起始节点出发的最长的路径。
在河流最长路径的问题中,河流信息通常以空间数据库的方式存储,不仅有地理要素的属性数据,还有空间数据[13]。利用这些地理要素的位置数据,就可以对搜索的路径进行启发。搜索过程中引入启发信息,可以省略大量无效的搜索路径,提高效率。
启发式算法计算最长路径算法描述如下:
(1) 确定待搜索的目标节点队列T。输入图中所有度为1的节点,即叶子结点,计算所有的叶子结点与起始点的距离Dn,并求解max{Dn}。计算第i个叶子结点到起始节点的距离Di,当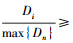
(2) 对河流图进行搜索。运用启发式搜索的思想,f(n)是节点n的估价函数,用f(n)=g(n)+h(n)进行估价[14-15]。其中,代价函数g(n)表示从当前节点m到扩展节点n之间弧段的长度,即lengthmn;评估函数h(n)表示从扩展节点n到目标节点t的欧氏距离,即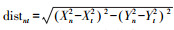
(3) 将节点n作为当前节点,按照步骤(2)的方法继续向下搜索,直到搜索到叶子结点,查看该叶子结点是否在待搜索的目标节点集合T中,若在,删除T中的该节点。
(4) 若目标节点集合为空,结束搜索;若不为空,选择当前节点为未完全搜索节点队列S的末尾节点,到步骤(2)继续搜索。
如在N3处,(N3,N7)与(N3,N4)为两条候选河段,且属性信息相同,因此需要用几何特征来选择主流河段。分别用启发式算法计算从N3出发经过N7和N4的最长路径,并进行比较选择主流。
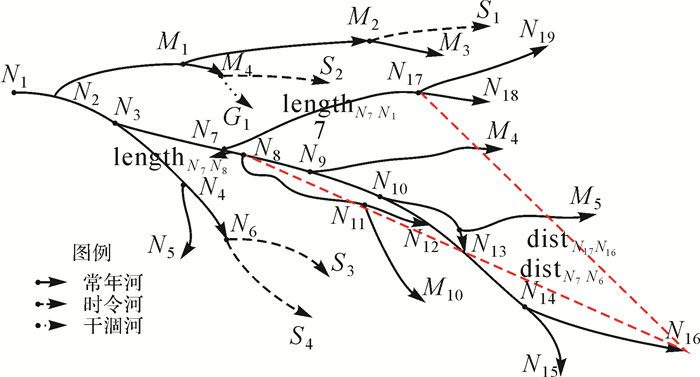
如图 7所示,计算从N3出发经过N7的最长路径。经过筛选后目标节点集合为{N15,N16},未完全搜索节点集合为空,当前状态空间的起始节点为N7,节点N7有两个可扩展节点N17和N8,选择目标节点为N16,f(N7,N17)=g(N7,N17)+h(N17)=lengthN7N17+distN17N16,f(N7,N8)=g(N7,N8)+h(N8,N17)=lengthN7N8+distN8N17,计算min{f(N7,N17),f(N7,N8)},因此f(N7,N8)较小,因此选择下一个节点为N8节点。同时,将节点N7放入未完全搜索节点集合中,继续搜索,直到搜索到目标节点N16,目标节点集合删除N16,未完全搜索集合放入节点N14。下一个目标节点为N15,从未完全搜索集合中取出最新放入的节点N14,继续搜索,搜索到N15,目标节点集合删除N15,集合为空,程序结束。
|
| 图 7 启发式算法选择主流 |
根据上述算法,求得从N3点出发分别经过N7和N4点的最长路径maxlengthN3N7、maxlengthN3N4。
在N8、N10节点处,河段有环,且环的类型为多入多出环,因此选择角度最好的河段作为主流河段,因此(N8,N9)、(N9,N10)、(N10,N12)、(N12,N13)为主流河段。
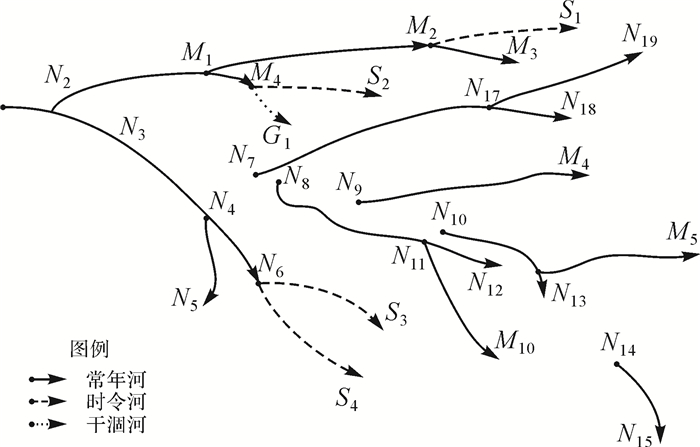
2.3 河流自动分级从N1节点搜索到N16节点为止,为一级河流。将一级河流从河系中去除,再进行迭代。图 8为迭代一次后的结果。
|
| 图 8 迭代一次后的结果 |
对主流上的节点继续搜索,直到所有河段都被搜索和分级过为止。最终的分级结果如图 9所示。
|
| 图 9 分级结果 |
试验平台基于WJ-Ⅲ无级地图工作站,开发环境基于Microsoft Visual Studio 2010,采用C++编程语言,试验测试的环境为单台PC机,系统版本为Windows 7,系统类型为64位操作系统,CPU为Intel Core i7-6700,主频为3.40 GHz,内存(RAM)为4 GB。试验数据采用地理国情监测的水系数据,对水系进行分级试验。水系数据中已有的信息包括:河流的流向、河流的类型、河流的名称。
试验利用两个地区的水系数据,对用启发式算法优化前和优化后的情况进行测试,见表 2。
| 指标 | 地区1 | 地区2 |
| 水系弧段总数/条 | 1093 | 13 012 |
| 完全遍历分级的时间/s | 1.984 | 15.05 |
| 启发式分级的时间/s | 1.881 | 12.71 |
| 提升时间率/(%) | 5.3 | 18.4 |
| 未优化的遍历弧段数/条 | 3189 | 42 532 |
| 优化的遍历弧段数/条 | 1961 | 35 521 |
| 减少遍历的比率/(%) | 62.6 | 19.7 |
| 启发式分级与完全遍历的差别数(差别率) | 0(0%) | 0(0%) |
由试验结果可以看出,对不同地区的河流数据进行分级的过程中,优化算法后,遍历的弧段数和时间都有不同程度的减少,但分级的结果相同,效率有所提高,且弧段总数越多,提升的时间越明显。对启发式算法的精确度和时间分析如下:
(1) 算法精确度:启发式算法与原算法的不同仅出现在对河流终结点的筛选中,可能将正确结果筛选掉。但在实际情况中,通过属性信息的分级后,运用该算法搜索的河流往往是一些较小的支流,通常短而直,因此正确的终结点被筛选掉的情况极少。
(2) 算法时间:在未优化的情况下,该算法是完全遍历,需要搜索每一个弧段,找出最长路径。优化后的算法首先会寻找符合条件的候选终结点,再通过启发信息对这些终结点进行寻找,通过减少搜索的次数来缩短算法的时间。优化后的最好情况下,在寻找最长路径时,目标节点只有一个,与起始节点构成一个最长路径,且每一次启发式选择的节点都是该条路径上的节点。此时,算法的总执行次数为最长路径上的节点的个数。在最差情况下,则需要对所有弧段进行遍历,与未优化时的情况相同。一般情况下,优化算法的时间介于最好和最差之间。
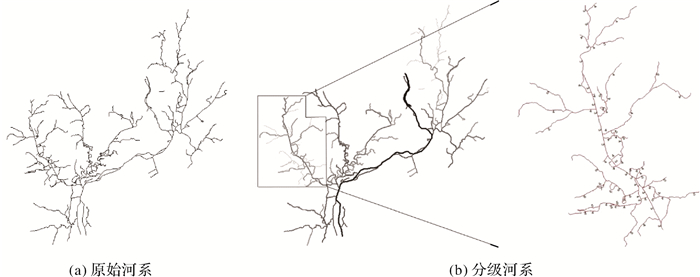
图 10(a)即为上述两试验地区之一的原始河系图。分级后的等级用颜色和粗细区分出来,其中颜色越深、线条越粗的代表的河系等级越高。从图 10(b)、(c)的河系分级结果可以看出,基于以上规则,分级取得了良好的效果,对河流等级识别准确,层次分明。尤其河系中出现复杂情况时,如河系中有环、节点处有多条弧段时,分级的效果优于已有的河流分级的算法,满足制图要求。
|
| 图 10 试验的分级结果 |
本文对河流分级的算法进行了改进,在准确性上,结合属性信息和几何特征的同时,通过对不同类型的环的处理,减少了复杂河流中尤其是有环河流的分级错误;在效率上,运用启发式算法改进了河系最长路径的算法,减少了搜索次数;并通过试验证明了该方法的有效性和合理性。在对河流分级的过程中,还可以考虑河流的更多几何特征,如河流的密度、河流的左右分支的数目等信息,以更进一步提升河流分级的准确性。
| [1] | 毋河海. 自动综合的结构化实现[J]. 武汉大学学报(信息科学版), 1996, 21(3): 277–285. |
| [2] | PAIVA J, EGENHOFER M J, FRANK A. Spatial Reasoning about Flow Directions:Towards an Ontology for River Networks[J]. International Archives of Photogrammetry and Remote Sensing, 1992, 24(B3): 318–324. |
| [3] | 郭庆胜, 黄远林. 树状河流主流的自动推理[J]. 武汉大学学报(信息科学版), 2008, 33(9): 978–981. |
| [4] | 吴伟, 李成名, 殷勇, 等. 有向拓扑的河系渐变自动绘制算法[J]. 测绘科学, 2016, 41(12): 89–93. |
| [5] | 张园玉, 李霖, 金玉平, 等. 基于图论的树状河系结构化绘制模型研究[J]. 武汉大学学报(信息科学版), 2004, 29(6): 537–539, 543. |
| [6] | 张青年, 全洪. 河系树的建立及其应用[J]. 中山大学学报(自然科学版), 2005, 44(6): 101–104. |
| [7] | 艾自兴. 地理信息系统中的河网平面结构模型及其自动建立[J]. 测绘, 1995(2): 75–79. |
| [8] | 郭庆胜. 河系的特征分析和树状河系的自动结构化[J]. 地矿测绘, 1999(4): 7–9. |
| [9] | 张青年. 线状要素的动态分段与制图综合[J]. 中山大学学报(自然科学版), 2004, 43(2): 104–107. |
| [10] | 艾自兴, 牛瑞芳, 毋河海, 等. 基于动态树结构的河网分析方法[J]. 测绘科学, 2006, 31(3): 80–81. |
| [11] | 谭笑, 武芳, 黄琦, 等. 主流识别的多准则决策模型及其在河系结构化中的应用[J]. 测绘学报, 2005, 34(2): 154–160. |
| [12] | 王建新, 杨志彪, 陈建二. 最长路径问题研究进展[J]. 计算机科学, 2009, 36(12): 1–4, 31. DOI:10.3969/j.issn.1002-137X.2009.12.001 |
| [13] | 邬伦, 刘瑜. 地理信息系统原理、方法和应用[M]. 北京: 科学出版社, 2001: 133-134. |
| [14] | 蔡自兴, 徐光祐. 人工智能及其应用[M]. 2版.北京: 清华大学出版社, 1996: 71-73. |
| [15] | 陆汝铃. 人工智能[M]. 北京: 科学出版社, 1996: 259-261. |


