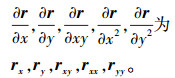2. 地理国情监测国家测绘地理信息局工程技术 研究中心, 陕西 西安 710064
2. National Administration of Surveying, Mapping and Geoinformation Engineering Research Center of Geographic National Conditions Monitoring, Xi'an 710064, China
车载或机载激光雷达(light detection and ranging, LiDAR)移动测量技术,能快速获取大面积、高密度、高精度的三维点云数据,是目前在大范围内采集地形原始数据最理想、最有效的方法和手段之一,已逐步成为我国高等级公路测设中最主要的地形数据来源[1]。然而,大面积、高密度的点云数据必然会导致数据量的大幅增加,在地形复杂区域,海量点云数据有助于地形特征的表达,而对于地形起伏不大、地势较平坦的区域,海量点云数据中则存在大量的冗余数据,这些冗余的数据不仅对地形的表达没有任何帮助,而且会消耗大量的存储空间,对数据的组织、处理、后期应用都带来了诸多不便[2]。如果能对原始点云数据进行有策略的抽稀精简,使得在减少点云数据量的同时,还能顾及地形特征,并保证地形精度,就可以有效地解决上述问题。因此,LiDAR点云数据抽稀是点云数据处理中的重要环节。
目前,国内外针对海量点云数据的抽稀算法可归纳为不顾及地形特征和顾及地形特征两种。
不顾及地形特征的抽稀算法中比较经典的有两种:①基于八叉树的格网抽稀[3]。该算法利用八叉树结构循环递归地将三维点云空间进行体元剖分,体元的大小控制着抽稀程度。②基于系统抽稀[4]。该算法首先确定采样间隔,然后按照采样间隔随机抽取一点予以保留。不顾及地形特征的抽稀算法主要应用于点云的快速显示。
顾及地形的抽稀算法主要有以下3种:①基于不规则三角网(TIN)的点云数据抽稀[5]。该算法首先对离散点云构建TIN, 然后计算某一点周围的三角面片间的法线偏差,并以此作为抽稀的判定条件。该算法能较好地顾及地形特征点,但是建立TIN的时间复杂度和空间复杂度大,效率低。②基于距离和高差的点云数据抽稀[6]。美国PAMELA女士提出的DDR(data density reduction)算法主要依靠两个参数:搜索半径及高差阈值。搜索半径用来指定邻域点云数据,高差阈值用来判定是否是冗余点。该算法利用高差作为判定条件只顾及了垂直方向上的地形特征。③基于曲率的点云数据抽稀[7-8]。该算法通过计算点云表面曲率作为抽稀判定条件,小于曲率阈值的点作为冗余点剔除,大于曲率阈值的点作为特征点予以保留。该算法能很好地顾及水平方向和垂直方向的地形特征,但是曲率阈值难以选取,而且在地势均匀变化区域(如公路路面、斜坡)会出现点云空洞,对于地形精度有一定影响。鉴于已有算法的优点和缺陷,本文提出一种改进的基于平均曲率的点云抽稀算法,该算法不仅顾及地形特征,减少冗余数据,还可避免点云空洞的出现。
1 改进的点云数据抽稀算法由于曲率反映了曲面性质的重要特征,因此它是描述地形特征的主要依据之一。目前曲率的计算一般采用的方法有:图像梯度求解法[9]、三角格网法[10]、二次曲面拟合法[11]。二次曲面拟合法计算简单、稳定性强、效率高,因此本文采用二次曲面拟合来计算曲率,其基本思路为:先取点云中任意一点pi(1≤i≤n,n为点云个数)的k个近邻点来进行二次曲面z(x, y)的拟合,再根据二次曲面的第一基本量和第二基本量来求出pi的平均曲率。二次曲面方程如下
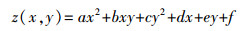 (1)
(1) 为了快速高效地得到海量点云数据中每个点的邻域信息,需要对原始点云数据建立空间索引。蒋晶钰等[12]认为KD-tree是一种组织LiDAR数据的有效方式。KD-tree由Bentley[13-14]于1975年首先提出,是一种分割k维数据空间的数据结构,主要应用于多维空间关键数据的搜索(如范围搜索和k近邻搜索)。本文采用三维KD-tree来实现k邻域搜索。KD-tree的核心技术包括建树和查找两个部分。
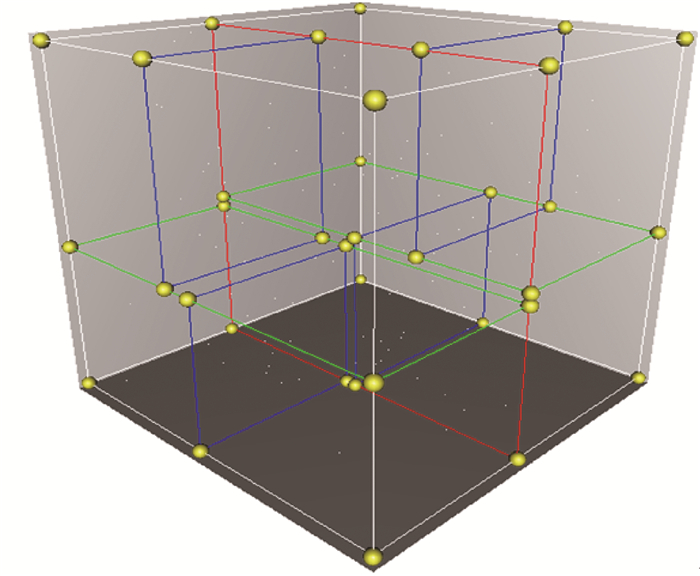
1.1.1 KD-tree的建立建立KD-tree的过程是一个递归的自顶向下的过程,将点云数据集所包含的整个三维空间作为根结点,用分割平面循环递归的按照X,Y,Z3个方向分裂,得到下级子空间作为中间结点,直到每个子空间所包含的点个数满足预先设定的值停止分割,并作为叶子结点。分割平面的选择通常采用以下几种规则[15]:标准差分割规则、中点分割规则、滑动中点分割规则。KD-tree的三维空间分割示意图如图 1所示。
|
| 图 1 KD-tree三维空间分割示意图 |
KD-tree的查找步骤与二叉树相同。在对点云数据集中的点进行k近邻查找时,在中间结点上根据分割该结点的分割平面的值与查找点对应维度的值的大小,决定是往左子空间查找还是往右子空间查找,最终搜索到所需要查找的叶子结点,在搜索过程中保存搜索路径。找到叶子结点后,在叶子结点中搜索k个近邻点,如果离查找点最远的近邻点的距离大于查找点到分割其父结点的分割平面的距离,则需要沿着搜索路径进行回溯,直到找到k个最近邻点。而进行范围查找时,是通过计算搜索路径上的点与查找点的距离是否小于搜索半径,来找到所有满足邻域条件的点集。
1.2 局部二次曲面的拟合国内外学者对邻域数据量k的确定做了大量试验,证明k值取24~30为最佳,太小不能满足精度要求,太大影响计算效率[16]。因此本文k取25来进行局部二次曲面的拟合。
由数据点pi和其k个邻域点,采用最小二乘法拟合局部二次曲面,建立目标函数为
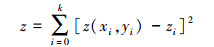 (2)
(2) 联立式(1)和式(2),对各项系数求偏导,并令偏导数等于零,得到线性方程组,见式(3),求解线性方程组,得到局部二次拟合曲面方程为
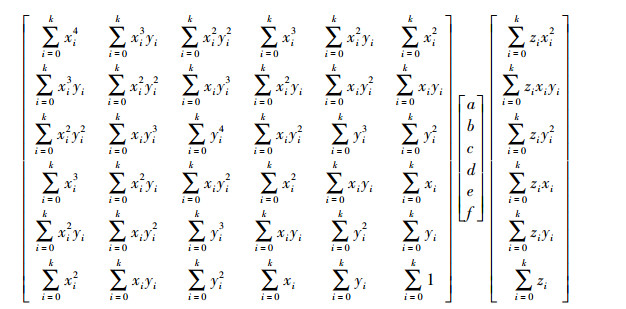 (3)
(3) 将式(1)写成曲面参数方程的形式,如下
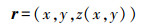 (4)
(4) 记曲面参数方程的偏导数
则二次曲面的第一基本量为
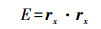 (5)
(5) 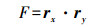 (6)
(6) 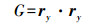 (7)
(7) 二次曲面第二基本量为
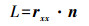 (8)
(8) 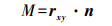 (9)
(9) 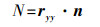 (10)
(10) 式中,n为单位法线
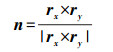 (11)
(11) 通过曲面的第一、第二基本量可求出局部曲面的高斯曲率K和平均曲率H为
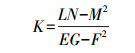 (12)
(12) 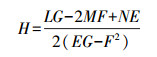 (13)
(13) 点云数据抽稀策略为:在顾及地形特征的前提下,点云抽稀后的点云密度应该与该点所在的曲面变化程度成正比,即在地势平坦区域(平均曲率小)多抽稀,地形复杂区域(平均曲率大)少抽稀。
传统的基于平均曲率的抽稀方法为设置一个曲率阈值,当某一点的平均曲率小于该阈值时,则将该点从点云中抽稀掉。首先,阈值难以确定,对不同点云阈值选取不同,一般采用经验阈值,需要人为设置;其次,由于公路点云数据的特殊性,其在公路路面处非常平坦,即路面上相邻点的曲率都非常小,抽稀后容易出现大面积点云空洞,对地形精度会有一定的影响。因此本文对传统的基于平均曲率的算法作了两方面改进,使其适用于公路点云数据的抽稀。具体步骤如下:
(1) 由目标点pi及其k个邻域点拟合局部二次曲面,并计算出平均曲率Hi,遍历所有点云。
(2) 将点云按平均曲率从小到大排序,依据抽稀率,将平均曲率排在前面的点设置标记flag=1,即待抽稀掉的非特征点,其他的点默认为0。
(3) 遍历被标记的点,进行半径为R的邻域搜索,如果搜索到的邻域点的flag全部为1,则将该点保留,并将flag设置为0,反之则抽稀掉该点。其中半径R表示在抽稀区域处允许出现的点云空洞范围上限,本文设置为3 m。
2 试验与分析为了检验本文算法针对公路点云数据的抽稀效果,在VS2013平台上使用C++编程语言实现了传统的基于曲率的抽稀方法和本文的改进算法。对京津唐高速公路一段点云数据(如图 2所示),共389 916个点,点云平均密度为2.4个/m2,进行抽稀试验,抽稀率设为50%。传统的平均曲率抽稀方法结果如图 3所示,本文改进算法抽稀结果如图 4所示。

|
| 图 2 原始点云 |

|
| 图 3 传统抽稀算法结果 |

|
| 图 4 本文抽稀算法结果 |
对比图 2—图 4可知,原始点云经过传统抽稀算法和本文抽稀算法处理后,点云数据明显减少,地形特征更加明显。
由于测量面积较大,图 3、图 4都进行了缩小显示,不易体现点云空洞的问题,因此本文还提供了抽稀结果的局部图。图 5是传统抽稀结果局部图,图 6是本文改进抽稀结果局部图。同时使用检查点法(检查点数为756个)评价抽稀后的点云数据生成数字高程模型的精度,统计信息见表 1。

|
| 图 5 传统抽稀结果局部图 |

|
| 图 6 本文抽稀结果局部图 |
| 抽稀方法 | 抽稀率/(%) | 剩余点数/个 | 中误差/m |
| 原始点云 | - | 389 916 | 0.086 |
| 传统算法 | 50.00 | 194 957 | 0.124 |
| 改进算法 | 49.91 | 194 606 | 0.091 |
对比图 5和图 6可发现,传统基于平均曲率的抽稀算法存在大面积的点云空洞问题,而本文算法则没有。结合表 1,可定量分析出在相同抽稀率下,由于点云空洞的存在使得传统算法的抽稀结果生成DEM的精度较低,而改进的算法抽稀结果生成DEM的精度较高,甚至与原始点云生成的DEM精度接近。
3 结语本文提出的用于公路点云数据的抽稀算法不仅顾及了地形特征,还解决了点云空洞的问题。在减少了LiDAR点云数据存储空间的同时,还保证了数据的质量。研究保证数据质量符合特定工程需求的最小抽稀率,从而最大限度地减少存储空间,是本文后续研究的重点。
| [1] | 赵文彦, 丁瑞. 遥感技术在公路测设中的应用综述[J]. 西部探矿工程, 2006, 18(5): 231–233. |
| [2] | 杜浩, 朱俊峰, 张力, 等. 顾及地形特征的LiDAR点云数据抽稀算法[J]. 测绘科学, 2016, 41(9): 140–146. |
| [3] | MARTIN R R, STROUD I A, MARSHAL A D. Data Reduction for Reverse Engineering, No.1068[R].[S.l.]:Computer and Automation Institute of Hungarian Academy of Science, 1996:63-69. |
| [4] | 缪志修, 齐华, 王国昌, 等. 基于机载LiDAR数据构建的DEM抽稀算法研究[J]. 铁道勘察, 2010, 36(4): 35–40. |
| [5] | CHEN Y H, NG C T, WANG Y Z. Data Reduction in Integrated Reverse Engineering and Rapid Prototyping[J]. International Journal of Computer Integrated Manufacturing, 1999, 12(2): 97–103. DOI:10.1080/095119299130344 |
| [6] | PAMELA S.A Data Density Deduction Algorithm for Post-processed Airborne Bathymetric Survey Data[D].Florida:University of Florida, 2000. |
| [7] | 周煜, 张万兵, 杜发荣, 等. 散乱点云数据的曲率精简算法[J]. 北京理工大学学报, 2010, 30(7): 785–789. |
| [8] | 蔡志敏, 王晏民, 黄明. 基于KD树散乱点云数据的Guass平均曲率精简算法[J]. 测绘通报, 2013(S1): 44–46. |
| [9] | 张济忠. 分形[M]. 北京: 清华大学出版社, 1995. |
| [10] | 龙毅. 扩展分维模型在地图目标空间信息描述中的应用研究[D]. 武汉: 武汉大学, 2002. |
| [11] | 王厚祥. 海图制图综合[M]. 大连: 大连舰艇学院, 1998. |
| [12] | 蒋晶珏, 张祖勋, 明英. 复杂城市环境的机载LiDAR点云滤波[J]. 武汉大学学报(信息科学版), 2007, 32(5): 303–306. |
| [13] | FINKEL R A, BENTLEY J L. Quad Trees a Data Structure for Retrieval on Composite Keys[J]. Acta Informatica, 1974, 4(1): 1–9. DOI:10.1007/BF00288933 |
| [14] | BENTLEY J L. Multidimensional Binary Search Trees Used for Associative Searching[J]. Communications of the ACM, 1975, 18(9): 509. DOI:10.1145/361002.361007 |
| [15] | ARYA S, MOUNT D M, NETANYAHU N S, et al. An Optimal Algorithm for Approximate Neraest Neighbor Searching[J]. Journal of the ACM, 1998, 45: 891–923. DOI:10.1145/293347.293348 |
| [16] | FALCONER K. 分形几何: 数学基础及其应用[M]. 曾文曲, 译. 沈阳: 东北大学出版社, 1991. |