2. 广西空间信息与测绘 重点实验室, 广西 桂林 541004;
3. 南宁市勘察测绘地理信息院, 广西 南宁 530022
2. Guangxi Key Laboratory of Spatial Information, Guilin 541004, China;
3. Nanning Exploration & Survey Geoinformation Institute, Nanning 530022, China
由于无人机影像具有较高的空间定位精度与地面分辨率,近年来在我国城市基础地理信息管理、城市规划等社会生产生活领域有广泛的应用[1-2]。
无人机影像的地面分辨率已经达到了毫米级,甚至更高,建筑物在该影像上的尺度、波谱、纹理特征与常规星载、机载遥感影像上的特征有一定区别,几何形状特征与普通高分影像相比更加显著。建筑物的角点决定了其轮廓的基本特征[3]。因此,对无人机影像建筑物角点的精确提取有着十分重要的理论和现实意义。
目前进行建筑物角点的检测与提取主要有以下两种方法:一种是从机载激光雷达数据中提取建筑物的激光角点,如罗伊萍通过支持向量机对单个激光点进行特征分类,从而有效地提取建筑物角点[4]。另一种是从光学影像中提取建筑物的角点。如Cui Shiyong等2008年用图搜索算法提取直角建筑物的角点,通过派生序列重建建筑物的形状[5],并在2012年根据Hough变换和循环检测的方法提取了复杂建筑物,并提高了提取精度[6]。Mustafa Turker和Dilek Koc-San通过集成的方法综合运用Hough变换和感知分组等方法标绘出建筑物屋顶形状,建筑物的提取精度为93.45%[7]。杜艺通过改进SUSAN算子提取航空影像中的特征点,从而成功提取出建筑物[8]。马潇潇通过改进的SVM算法对无人机影像中建筑物进行分类,分类精度为94.74%[9]。吴秀芸利用高斯函数计算建筑物边界曲线的曲率提取候选角点集,并通过动态曲率阈值代替固定的阈值筛选出正确的建筑物角点[10]。崔有祯通过改进的Harris算法提取建筑物的角点,并利用4种改进梯度算子提高了建筑物角点检测的成功率,建筑物角点检测正确率为89%[11]。
综上所述,建筑物角点检测和提取都是先依据灰度信息独立提取房屋角点,再依据屋顶的几何约束信息构建角点匹配规则提取建筑物[12],以上方法虽然能提取出建筑物的角点,但是部分建筑物角点被遮挡增加了提取难度。本文基于建筑物边缘角点检测和角点分类的综合方法提取建筑物,首先使用Harris算法提取边缘点集,然后基于SVM分类法对边缘点集进行匹配分类。
1 基于SVM的高分辨率影像建筑物角点提取方法 1.1 方法步骤基于SVM的无人机影像建筑物角点提取步骤(如图 1所示)如下:

|
| 图 1 基于SVM的建筑物角点提取方法流程 |
(1) 对影像进行图像预处理。根据植物和水体的特性,通过ENVI等影像处理软件得到影像的归一化植被指数,这样可以减少植被等对建筑物角点提取产生的干扰,从而提高建筑物角点的提取精度。
(2) 选取适当分割尺度参数,通过面向对象方法对建筑物进行区域分割。
(3) 通过Harris算法对分割后的影像进行建筑物边缘点粗提取,得到建筑物边缘点集。
(4) 选择训练样本。从边缘点集中随机选取部分点作为样本点,样本点分为建筑物角点和非建筑物角点。
(5) 特征提取。根据影像的特征提取部分属性值作特征向量,以此作为分类依据。
(6) 构建训练模型。为了获得高精度的检测结果,将样本映射到高维的特征空间,选择高斯径向基函数为核函数[13],进行SVM训练,得到模型分类器参数。
(7) SVM分类运算。对建筑物边缘点集进行分类提取,对建筑物角点提取结果进行精度评价。
1.2 Harris算子计算在影像中设置一个局部小区域窗口,并让其按照一定规则移动,遍历影像中每一个像素点,考察窗口的平均灰度变化,计算图像中的每个像素点在水平方向和垂直方向上的梯度,以及两者的乘积,构建自相关矩阵M
 (1)
(1)  (2)
(2) 式中,ω(u, v)为离散二维零均值高斯函数。对图像进行高斯滤波,离中心点越近的像素赋予越大的权重,以减少噪声影响。
M的特征值δ1、δ2能够反映像素点周围的结构特征,因此可以根据δ1、δ2来提取影像的角点和边缘,但是Harris算子不需要计算具体的特征值,而是定义角点响应值R来判断角点,特征值是隐含在detM和traceM中
 (3)
(3) 式中,detM为矩阵M的行列式;traceM为矩阵M的直迹;α为经验常数。
计算每一个像素的角点响应值R,对小于某一阈值的R设置为零,大于阈值的R保留,在一个n×n的邻域内进行非极大值抑制,即某一像素的角点响应值R为邻域极大值,则判别该像素为建筑物边缘点。
1.3 特征向量构建支持向量机分类技术中,特征向量的选择和提取是重要环节。在输入训练点集后,需要提取影像的属性特征,构建特征向量,以作为SVM分类器的输入训练数据。根据不同类型的无人机影像,选取不同的属性特征。一般情况下,多列举与分类有关的特征,可以充分利用各种有用的信息,改善分类精度。
本文特征向量选择方案如下:根据影像中建筑物边缘互相垂直的特性,可以分离建筑物的角点和边缘线上的点。观察建筑物边缘点集图可知:对任意一点A,找到与之距离最近的两个点B和C,拟合成角∠BAC,计算角度ρ=∠BAC。以坐标原点为基准,建筑物角点大致分为4个方向上的点,计算每一个点到原点的距离d,设置一定的取值范围,在范围以内的点为建筑物角点。通过Harris算子的二阶梯度, 计算边缘点集的响应值R,对小于某一阈值的R设置为零,大于阈值的R保留,在一个n×n的邻域内进行非极大的邻域内进行非极大值抑制,最终保留的像素点为建筑物角点。综上可以构建特征向量
1.4 角点SVM构建通过Harris算子获得建筑物的边缘点集,从建筑物边缘点集中随机选取部分点作为样本集(xi, yi),其中i=1, 2, …, n, n为样本数,xi∈Rd为建筑物角点样本的特征向量,yi∈(0, 1)为特征向量的分类标识,其中0表示非建筑物角点,1表示建筑物角点。通过构建角点SVM对建筑物边缘点集进行分类:首先通过高斯径向基函数将建筑物边缘样本点映射到高维特征空间,如下
 (4)
(4) 在这个高维线性空间中构造最优分类超平面,最大间隔将建筑物角点和非建筑物角点分隔开,如下
 (5)
(5) 式中,ω∈R(d), b∈R(d)的都进行了规范化。引入一个非负松弛变量ξi放宽约束条件,能够在最大限度上满足大部分数据的分类正确,最优分类超平面问题可以描述为
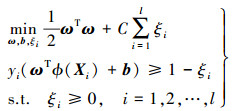 (6)
(6) 式中,C为惩罚参数,C越大表示对错误分类的惩罚越大。
采用拉格朗日乘子法求解建筑物角点二分类问题,即
 (7)
(7) 式中,αi、βi为拉格朗日乘子,0≤αi, 0≤βi。由此得到
 (8)
(8)  (9)
(9)  (10)
(10) 将式(8)、式(9)、式(10)代入式(7)得到对偶最优化问题
 (11)
(11) 由式(11)得到决策函数和参数b分别为
 (12)
(12)  (13)
(13) 式中,sign(·)为符号函数;αi为拉格朗日乘子,0≤αi;NNSV为标准支持向量数;JN为标准支持向量的集合;J为支持向量的集合;b是分类阈值。
选择适当的惩罚系数C与核函数宽度g,通过以上步骤,构建角点SVM分类模型。
2 试验 2.1 试验数据及预处理为了验证本文前面提出的方法,选择输入数据为广西某地无人机航拍影像,影像大小为764×375像素, 含可见光及近红外4个波段,该区域原始影像如图 2所示。考虑到影像中植被的叶绿素在波长0.65~0.7 μm的谱段形成强吸收带,通过近红外与红光波段反射率的归一化比值提取植被信息,归一化植被指数(NDVI)可以使植被区域和非植被区域分离开, 使用ENVI软件对影像进行NDVI植被指数计算,计算结果如图 3(a)所示。通过Matlab 2013a编程平台对去除植被干扰的影像进行面向对象分割,粗建筑物轮廓提取如图 3(b)所示。

|
| 图 2 研究区无人机影像 |

|
| 图 3 试验数据预处理结果 |
对预处理的影像进行建筑物边缘点集计算。通过Harris算子从水平和垂直方向上对影像进行梯度计算,获得图像Ix与Iy,同时x, y方向进行协方差相乘获得图像Ixy。采用高斯函数对图像进行边缘增强,设置高斯窗函数为[7×7],sigma值设置为2,计算每一个像元点响应值R,设置阈值T为R中最大值的0.01倍,并对小于阈值T的R置为零。在[7×7]的邻域内进行非极大值抑制,局部极大值点即为建筑物边缘点。
试验首先选取经验常数α=0.04,计算所得边缘点为251个,如图 4(a)所示,发现建筑物边缘点有聚簇现象,后来选取经验常数α=0.2,计算所得边缘点为116个,如图 4(d)所示,发现部分角点有缺失现象;选择经验常数α=0.06,计算所得边缘点为255个,如图 4(c)所示;选择经验常数α=0.08,计算所得角点为231个,如图 4(b)所示。

|
| 图 4 不同经验值α计算的边缘点集图 |
分析图 4发现, α值较大时,边缘点与角点的数量减少,增大角点检测误差;α值较小时,边缘点与角点的数量增加,产生点聚簇现象,增大分类计算复杂度。因此,本文选择经验常数α=0.1,这样可以保证在不缺失建筑物角点的前提下,降低检测候选点的数量,提高检测效率。计算结果见表 1。
表 1是Harris算子对影像进行梯度计算的结果:在x方向与y方向的一阶梯度的最大值与最小值相同,根据梯度的计算值Ix与Iy与x、y方向协方差相乘值Ixy构建自相关矩阵M
由矩阵M计算角点响应值R,其中Rmax=1.863×108, 选择阈值T=0.01×Rmax=1.863×106对R进行非极大值抑制后,计算所得边缘点为202个,边缘点集如图 5所示。
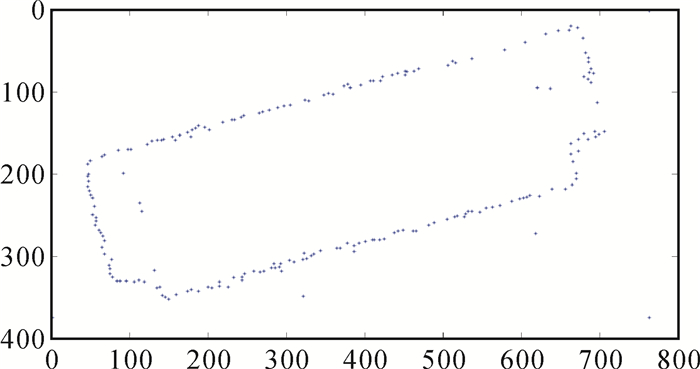
|
| 图 5 由Harris计算的建筑物边缘点集图 |
根据试验中影像的特点,结合前文特征向量构建方法,为描述建筑物角点与边缘点的特征,选择任3个角点之间组成的角度值ρ、每一个点与原点的距离d、影像二阶梯度计算的角点响应值R 3个属性特征,构建特征向量SV=[ρ d R]T。
对边缘点集中任意一点A,寻找与之距离最近的两个点B和C,拟合成角∠BAC,计算角度ρ=∠BAC。若ρ≈90°,则i为建筑物角点;若ρ≈180°,则A为建筑物边缘线上的点,否则A为干扰噪声点。根据这个特点计算每一个点的角度ρ,ρ的取值范围见表 2。
以坐标原点(图像左上角)为基准,建筑物角点大致分为4个方向上的点,计算每一个点到原点的距离d,设置一定的取值范围,在范围以内的点为建筑物角点。距离d的范围见表 3。
通过Harris算子的二阶梯度计算边缘点集的响应值R,对小于某一阈值的R设置为零,大于阈值的R保留,在一个n×n的邻域内进行非极大值抑制,最终保留的像素点为建筑物角点,见表 4。
试验在Matlab 2013a编程环境中完成,通过libsvm3.21工具箱构建角点SVM模型,从前文计算的边缘点集202个点中随机选取部分点作为样本点。本试验中随机选取了179个样本点,含角点与非角点两种类型,手动将样本点中的建筑物角点标记为1,非建筑物角点标记为0,构建模型时缺省核函数为高斯径向基函数,参数C和g采用基于交叉验证的网格搜寻方法来取值,最终选择惩罚参数C=2,核函数宽度g=0.01,采用最佳参数C与g对整个训练集进行训练获取支持向量机模型,训练结果信息见表 5。
表 5中, #iter为迭代次数,Nu为设置nu-SVC中参数nu值,Obj为求解二次规划问题的最小值,rho为记录的决策函数中常数项b,nsv是指支持向量个数为179个,nbsv是指位于边界的支持向量个数。训练模型构建完成后,文件显示为一个结构体变量,记录了得到的分类模型中的各种参数构成的结构体量(见表 6)。
| 参数类型 | Parameters | nr_class | TotalSV | rho | Lable |
| 参数值 | [0;2;3;0.01;0] | 2 | 179 | -0.9155 | [0, 1] |
表 6中SVM模型中记录了libsvm_options的参数选项[-s-t-d-g-r], 其中s=0指本模型中选择的libsvm类型为分类问题专用的C-SVC,t=2指构建模型时选择的核函数类型为径向基RBF函数,d=3指核函数多项式中的degree设置为3次,g=0.01指该核函数宽度为0.01,r=0指核函数中的coef0项,是针对多项式和sigmoid核函数的,缺省值为0。nr_class为2指待分类的点一共被分成了两类;TotalSV=179记录了总的支持向量的个数;rho=-0.915 5为决策函数中常数项b的相反数:Lable中记录了所分类别的标签,因为是二分类问题,所以只有0和1两个值,表示将建筑物的边缘点集分成了两类。除了上述信息,该模型文件中还详细记录了支持向量的索引目录sv_indices、具体支持向量值SVs、决策函数中支持向量的系数sv_coef。
2.4.2 建筑物角点提取使用SVM分类模型,对202个建筑物边缘点集进行分类,分类结果如图 6所示,其中建筑物角点10个,错分角点有2个,非建筑物角点192个,整体分类精度较高,将所提取的角点连接到一起,可以成功提取出建筑物。在最后通过SVM模型对角点分类提取时运行时间为2.014 s,效率较高。

|
| 图 6 SVM法识别与提取的建筑物角点 |
分类前后结果对比如图 7所示,成功从图 7(a)中的202个点中提取出建筑物角点,其中图 7(b)中灰色的点表示提取的建筑物角点。根据提取的结果,成功标绘出建筑物的位置和大小。
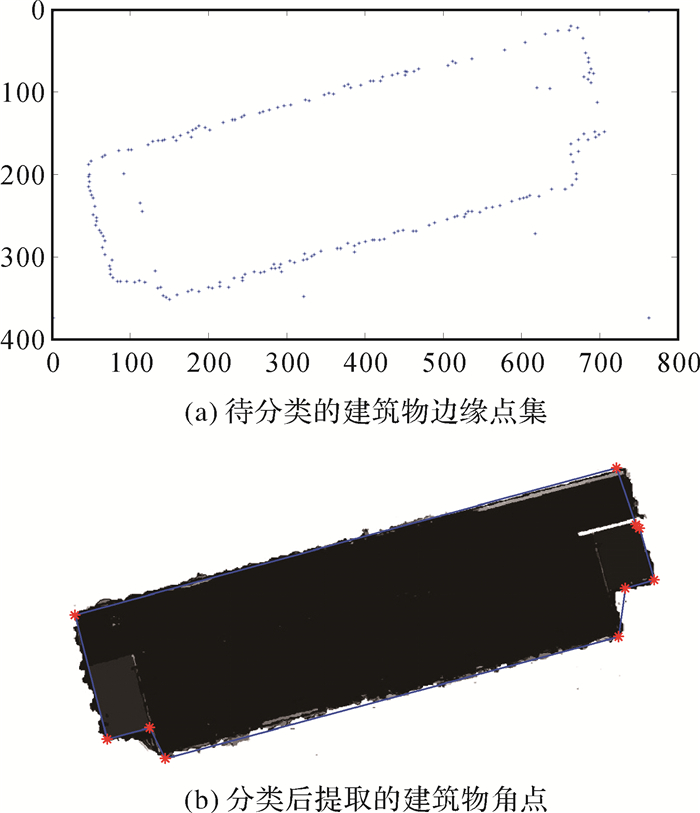
|
| 图 7 建筑物边缘点集分类前后对比 |
为验证分类效果, 分别从角点分类精度和提取的建筑物面积两方面对分类结果进行对比分析。首先, 从表 7可以看出, 在通过SVM分类方法进行建筑物角点提取时,漏检角点数为0,错检角点数为2,这是因为建筑物屋顶部分纹理和亮度值变化较大,相对比较难区分建筑物角点和边缘点,因此将2个边缘点错分为建筑物角点。
本文针对无人机影像中单个建筑物角点的快速识别,通过原理分析与试验研究提出了一种基于支持向量机的角点分类检测方法。在研究中使用了广西某地无人机的4波段光学、红外影像。为了保证算法的泛化能力,随机选取了179个样本点对建筑物边缘点集进行训练获取本文的SVM模型,成功提取建筑物角点。
与目前角点提取方法相比,本文提出的方法可以在保证分类精度的同时降低运算的复杂度,提高建筑物角点检测的精度,可进一步提取出轮廓清晰,形状完整的建筑物。
| [1] | 史先琳, 杨武年. 城市基础地理信息与公共平台数据差异与转换[J]. 测绘通报, 2014(6): 89–91. |
| [2] | 雷添杰, 李长春, 何孝莹. 无人机航空遥感系统在灾害应急救援中的应用[J]. 自然灾害学报, 2011, 20(1): 178–183. |
| [3] | 赖祖龙, 申邵洪, 程新文, 等. 基于图斑的高分辨率遥感影像变化检测[J]. 测绘通报, 2009(8): 17–20. |
| [4] | 罗伊萍, 姜挺, 王鑫, 等. 支持向量机的建筑物激光脚点提取方法[J]. 测绘科学, 2011, 36(4): 173–175. |
| [5] | CUI Shiyong, YAN Qin, LIU Z J.Right-angle Building Extraction Based on Graphsearch Algorithm[C]//2008 International Workshop on Earth Observation and Remote Sensing Applications.[S.l.]:[s.n.], 2008. |
| [6] | CUI Shiyong, YAN Qin, REINARTZ P. Complex Building Description and Extraction Based on Hough Transformation and Cycle detection[J]. Remote Sensing Letters, 2012, 3(2): 151–159. DOI:10.1080/01431161.2010.548410 |
| [7] | TURKER M, KOC-SAN D. Building Extraction from High-resolution Optical Spaceborne Images Using the Integration of Support Vector Machine (SVM) Classification, Hough Transformation and Perceptual Grouping[J]. Inteniational Journal Applied Earth Observation and Geoinformation, 2015, 35(5): 58–69. |
| [8] | 杜艺, 龚循平. 利用改进的SUSAN算法提取航空影像中孤立的特征点[J]. 测绘科学, 2011, 36(6): 131–132, 94. |
| [9] | 马潇潇, 张光胜, 李长春, 等. 改进支持向量机算法无人机影像信息精确提取[J]. 测绘科学, 2015, 40(3): 47–51. |
| [10] | 吴秀芸, 李艳, 周华. 基于角点检测的建筑物轮廓矢量化方法[J]. 遥感信息, 2011(5): 95–99. |
| [11] | 崔有祯, 吴露露, 辛星, 等. 基于改进Harris算法的高分辨率遥感影像建筑物角点检测研究[J]. 测绘通报, 2013(9): 24–26. |
| [12] | 严岩. 高空间分辨率遥感影像建筑物提取研究综述[J]. 数字技术与应用, 2012(7): 75–76, 78. |
| [13] | 闫丽丽. 基于散射特征的极化SAR影像建筑物提取研究[D]. 徐州: 中国矿业大学, 2013. |





