2. 西北大学信息科学与技术学院, 陕西 西安 710127;
3. 北京师范大学信息科学与技术学院, 北京 100875
2. Shool of Information Science and Technology, Northwest University, Xi'an 710127, China;
3. School of Information Science and Technology, Beijing Normal University, Beijing 100875, China
近年来随着三维扫描技术的迅速发展,各种各样的三维点云数据采集设备应运而生。三维扫描仪一次扫描只能获取物体表面的部分点云信息,要想获取其全局信息,需要进行多次扫描,再通过点云配准技术来实现。点云配准是三维建模的关键技术之一,其主要目的是求解不同设备或角度采集到的两个点云的最优空间变换,使其能够达到最佳配准。目前,点云配准已经在三维重建[1-2]、地面场景配准[3]、目标识别[4-5]以及颅面复原[6]等领域得到了广泛的应用。
目前的点云配准算法中,应用最为广泛的是由P.J.Besl等[7]提出的迭代最近点(iterative closest point, ICP)算法,该算法简单,易于理解和实现,但是算法的运行效率较低,而且对两个点云的初始位置要求较高。鉴于此,国内外学者提出了很多改进的ICP算法[8-13]。虽然这些改进算法在点云配准的精度、速度及抗噪性等方面有了一定程度的提高,但是依旧不能很好地描述点云的局部特征,而且对于低覆盖率的点云的配准效果也不佳。
针对低覆盖率的点云,本文提出一种基于二维局部特征的点云配准算法。算法主要思想为:首先采用基于区域层次上的自动点云配准算法实现粗配准;然后将三维点云转换成二维图像,并采用SURF算法提取两幅二维图像的特征点;最后根据二维匹配点获取两个点云的三维相关点,并采用最小二乘逼近法计算最优旋转矩阵,由此实现点云的快速精确配准。
1 粗配准算法粗配准采用基于区域层次上的点云配准方法[14],分为区域划分、区域配准、求解组合系数以及求解刚体变换等4个基本步骤。
(1) 进行区域划分。对于待配准的两个点云,分别对其均匀采样,然后计算每个采样点的基于欧氏距离的Voronoi图作为划分的区域,即以均匀采样点为初始聚类中心,执行多次基于欧氏距离的C-均值聚类,即可将每个点云划分为一系列互不相交的区域。通常,划分区域的数目与物体的形状和点云的重叠比例有关,通常设置为1~20个。
(2) 进行区域配准。与点云配准相比,区域配准是一种规模更小的配准过程,因此这里采用穷举法将两个点云中的所有对应区域对进行配准,并按照配准后两个区域的重叠比例来评价配准的效果。
(3) 求解组合系数。这里引入可信性和一致性的概念,通过最大化能量函数来求解组合系数,该能量函数定义为
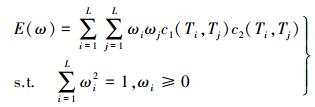 (1)
(1) 式中,ω={ωi}i=1L,为待求解的组合系数;c1(Ti, Tj)和c2(Ti, Tj)为可信性信息,即真实的全局刚体变换的可能性。
(4) 求解刚体变换。上个阶段求解的线性变换一般不是刚体变换,因此要将该线性变换分解为一个旋转矩阵R和一个平移向量t,这里的R采用四元数法[15]表示
 (2)
(2) 式中,q0≥0, q02+q12+q22+q32=1,R可通过下面的约束优化问题求得
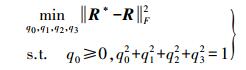 (3)
(3) 通过以上4个基本步骤,即可完成两个点云的粗配准,将两个点云初步对齐后,即可采用基于D局部特征的点云配准算法实现细配准。
2 三维点云转换成二维图像 2.1 BA图像通常三维图像的深度图像用于将三维点云转换成二维图像,不能用于表示三维点云中的点及其邻域点之间的关系。与深度图像不同,BA图像(bearing angle image)[16]可以突出由角度形成的边缘,因此可以从中提取到更多的信息。
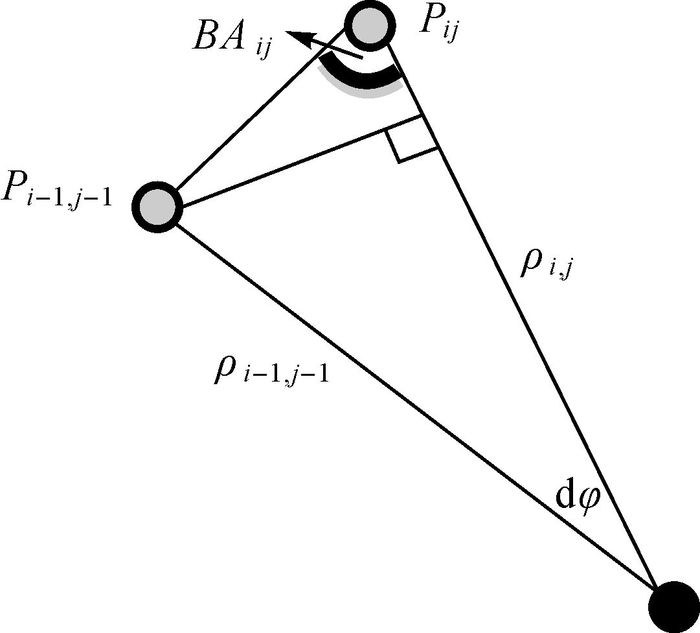
对于一个三维形状的物体,其BA图像的像素灰度水平定义为从该点到一个连续点的激光束和矢量之间的夹角,如图 1所示。点pij和pi-1, j-1是两个测量点,点o是点云的源点,也就是扫描仪的位置,点pij的角度值BAij定义为
|
| 图 1 BA图像的像素灰度水平 |
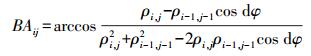 (4)
(4) 式中,ρi, j为第i个扫描层的第j个扫描点的测量值;ρi-1, j-1为第i-1个扫描层的第j-1个扫描点的测量值;dφ为相应的角度增量。
2.2 BA图像特征提取和匹配前文已将三维参考点云和目标点云转换成了二维的BA图像,下面采用基于特征的匹配方法来寻找BA图像的相关点,即采用SURF(speed-up robust features)算法[17-18]来实现。
SURF算法是一个尺度不变的二维图像特征检测方法,与SIFT算法相似,SIFT算法比较稳定,检测特征点更多,但是复杂度较高,而SURF要运算简单,效率高,运算时间更短。SURF算法由以下几个步骤组成:①构建黑森(Hessian)矩阵;②生成尺度空间;③利用非极大值抑制初步确定特征点和精确定位特征点;④构造SURF特征点描述子。
SURF提取的特征描述子可以确定特征点主方向及其邻近点的64个特征矢量。BA图像的特征点的匹配是通过计算两个特征矢量的欧几里得距离来实现的。匹配完成后,即可找到BA图像的相关特征点。
3 求解三维变换矩阵对于BA图像的任意一个像素点,BAij就对应初始三维点云中的第i个扫描层的第j个扫描点。三维点和二维像素是一种一对一的映像,因此二维图像像素BAij的初始三维点就是pij。
下面求解两个三维点云的最佳刚体变换。设两个待配准的三维点云为P和Q,它们通常有多于3对的相关点,因此求解P和Q的旋转矩阵的问题可以看作是一个正交Procrustes问题。首先,假设平移是从P的质心到Q的质心。因此,不考虑平移变换的情况下,两个点云可以写为
 (5)
(5) 式中,p和q分别为点云P和Q的质心,其计算式为
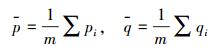 (6)
(6) 令新的相关点云分别为云Pc和Qc的。由于最佳旋转角R意味着最小的变换误差,因此R可表示为
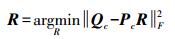 (7)
(7) 式中,||·||F为Frobenius范数,定义为
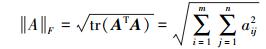 (8)
(8) 因此优化形式可以进一步写为
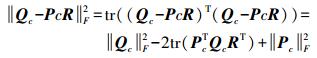 (9)
(9) 由于||Qc||F2和||Pc||F2都是常量,因此最小化式(9)的问题可转化为
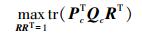 (10)
(10) 由于R是一个正交矩阵,因此该约束优化问题可以采用拉格朗日乘子来求解。拉格朗日乘子定义为
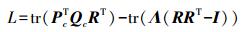 (11)
(11) 由于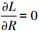
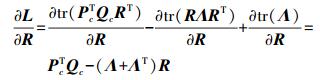 (12)
(12) 式(12)可进一步写为
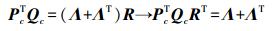 (13)
(13) 令PcT Qc的SVD为UΣVT,于是有
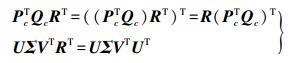 (14)
(14) 式中,Σ=diag(σ1(PcTQc), …, σn(PcTQc))。
由式(14)可计算出,最佳旋转矩阵为
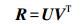 (15)
(15) 因此,最佳刚体变换可表示为
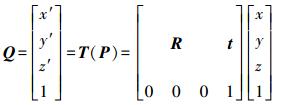 (16)
(16) 式中,t=q-p,且R=UVT,由此通过该刚体变换实现了两个三维点云的细配准。
4 试验结果与分析试验数据源于Stanford 3D Scanning Repository[19],采用了两个兔子点云数据,如图 2所示。

|
| 图 2 待配准点云 |
试验在CPU为Intel core i3 2.27 GHz,内存为2 GB的32位Win7操作系统上实现配准。对于图 2所示的点云数据,直接采用ICP算法进行配准,其配准结果如图 3所示。

|
| 图 3 直接使用ICP算法的配准结果 |
显然配准结果很不理想,主要是由于ICP算法对两个点云的初始位置要求较高,而且对低覆盖率点云的配准结果较差。因此本文首先采用基于区域层次的自动点云配准算法实现粗配准,粗配准结果如图 4所示,然后再分别采用ICP算法和本文提出的基于二维图像特征的点云配准算法实现细配准,其细配准结果分别如图 5和图 6所示。

|
| 图 4 粗配准结果 |

|
| 图 5 ICP算法的细配准结果 |

|
| 图 6 本文算法的细配准结果 |
在细配准阶段,ICP算法和本文提出的基于二维图像特征的配准算法的配准误差、算法耗时等参数见表 1。
从图 4—图 6及表 1的配准结果来看,基于区域层次的自动点云配准算法能够将两个点云粗略配准,ICP算法和基于二维图像特征的点云配准方法均可实现两个点云的细配准,但是基于二维图像特征的点云配准方法的配准精度和速度要比ICP算法分别提高了20%和60%。因此,本文的点云配准算法是一种快速、精确的点云配准算法。
5 结语点云配准是三维建模的一个关键步骤,其应用范围涉及多个领域。本文利用二维图像特征,提出了一种快速、高精度的低覆盖率点云配准方法。该方法首先通过区域划分、区域配准、求解组合系数及求解刚体变换等步骤快速实现点云的粗配准,然后基于二维图像特征提出了一种快速、高精度的点云的细配准算法,由此实现了点云的精确配准。在以后的点云配准算法研究中,要综合考虑多种因素,作进一步的深入研究,如进一步完善二维特征提取算法,以提高点云配准精度;针对点云中存在的问题作进一步的研究,提高算法的抗噪性;将点云配准算法应用到兵马俑碎块拼接或颅面复原研究中,以扩大算法的应用范围。
| [1] | LUO Y, GUAN T, WEI B, et al. Fast Terrain Mapping from Low Altitude Digital Imagery[J]. Neurocomputing, 2015(156): 105–116. |
| [2] | 闫阳阳, 李永强, 王英杰, 等. 三维激光点云联合无人机影像的三维场景重建研究[J]. 测绘通报, 2016(1): 84–87. |
| [3] | 郑敏辉, 臧玉府, 梁福逊, 等. 不同场景的地面激光点云配准方法研究[J]. 测绘通报, 2015(8): 30–34. |
| [4] | GAO Y, WANG M, TAO D, et al. 3-D Object Retrieval and Recognition with Hypergraph Analysis[J]. IEEE Transactions on Image Processing, 2012, 21(9): 4290–4303. DOI:10.1109/TIP.2012.2199502 |
| [5] | GAO Y, WANG M, JI R, et al. 3-D Object Retrieval with Hausdorff Distance Learning[J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 2088–2098. DOI:10.1109/TIE.2013.2262760 |
| [6] | 税午阳, 周明全, 武仲科, 等. 数据配准的颅骨面貌复原方法[J]. 计算机辅助设计与图形学学报, 2011, 23(4): 607–614. |
| [7] | BESL P J, MCKAY N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 14(2): 239–256. |
| [8] | ZHU J, DU S, YUAN Z, et al. Robust Affine Iterative Closest Point Algorithm with Bidirectional Distance[J]. Iet Computer Vision, 2012, 6(3): 252–261. DOI:10.1049/iet-cvi.2011.0178 |
| [9] | HAN J, YIN P, HE Y, et al. Enhanced ICP for the Registration of Large-scale 3D Environment Models:An Experimental Study[J]. Sensors, 2016, 16(2): 1–15. DOI:10.1109/JSEN.2015.2493738 |
| [10] | DU S, LIU J, ZHANG C. Probability Iterative Closest Point Algorithm for m-D Point Set Registration with Noise[J]. Neurocomputing, 2015(157): 187–198. |
| [11] | DU S, ZHENG N, XIONG L. Scaling Iterative Closest Point Algorithm for Registration of m-D Point Sets[J]. Journal of Visual Communication and Image Representation, 2010, 21(5-6): 442–452. DOI:10.1016/j.jvcir.2010.02.005 |
| [12] | ZHAO L, SHEN X, LONG X. Robust Wrinkle-aware Non-rigid Registration for Triangle Meshes of Hand with Rich and Dynamic Details[J]. Computers & Graphics, 2012, 36(5): 577–583. |
| [13] | 戴玉成, 张爱武. 三维激光扫描数据快速配准算法研究[J]. 测绘通报, 2010(6): 8–11. |
| [14] | 韩宝昌, 曹俊杰, 苏志勋. 一种区域层次上的自动点云配准算法[J]. 计算机辅助设计与图形学学报, 2015, 27(2): 313–319. |
| [15] | HORN B K P. Closed-form Solution of Absolute Orientation Using Unit Quarternions[J]. Journal of the Optical Society of American, 1987, 4(4): 629–642. DOI:10.1364/JOSAA.4.000629 |
| [16] | SCARAMUZZA D, HARATI A, SIEGWART R.Extrinsic Self Calibration of a Camera and a 3D Laser Range Finder from Natural Scenes[C]//Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems.San Diego:IEEE, 2007:4164-4169. |
| [17] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-up Robust Features(SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346–359. DOI:10.1016/j.cviu.2007.09.014 |
| [18] | Bay H, Tuytelaars T, VAN GOOL L.SURF:Speeded Up Robust Features[C]//Computer Vision-ECCV 2006.Berlin:Springer, 2006:404-417. |
| [19] | Stanford Computer Graphics Laboratory.The Stanford 3D Scanning Repository[EB/OL].(1996-9-10)[2016-06-15].http://graphics.stanford.edu/data/3Dscanrep. |


