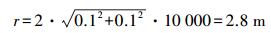2. 中国土地勘测规划院, 北京 100035
2. Chinese Land Surveying and Planning Institute, Beijing 100035, China
正在开展的新一轮土地利用现状更新调查工作,按照继承和创新的原则,充分继承年度土地变更调查成果,利用互联网+核查新技术手段,提高调查工作效率,确保调查成果准确性。具体技术路线是:采用国家2000坐标系,最新优于1 m的遥感影像,将城镇土地利用调查比例尺提高到1:2000,继承年度土地变更调查成果,判读提取全要素土地利用调查地类信息,同时,明确了数据的检查与核查机制,对更新过程有了更加严格规范的要求,采用计算机自动比对和人机交互检查方法,对县市报送成果逐图斑内业比对,提取调查初步成果、上年度基础数据库和国家内业判读结果之间的差异图斑,据此开展外业实地核查,对外业图斑进行认定,拍摄图斑实地照片,最终将调查成果报送至国家。
由于近年来面向各行业特定需求的专项调查工作蓬勃开展,同一空间区域可为新一轮土地利用现状调查借鉴复用的多尺度矢量空间数据比较多,同名复合要素的地理表达也较复杂,在数据模型、时相、分级分类、空间基准、属性编码及几何位置等诸多方面存在不一致,定量评判同名要素之间的一致性和完整性不仅决定了不同尺度的地理特征能否被准确客观地表达,也直接表征了空间数据质量的优劣[1-2]。空间数据匹配是多尺度空间数据融合、差异检测、数据更新等技术的基础和关键。
土地利用现状更新调查中地物复合要素是由点、线、面3类几何要素构成的,因此复合要素之间的匹配研究也最终转化为对3类要素之间同构或异构匹配方法的剖析。近年来,国内外专家对空间匹配问题进行了深入研究,取得了良好效果。通常点要素匹配常利用模糊集理论[3-4]来解决独立点状地物的匹配问题。线要素匹配大部分都是针对道路网数据展开匹配研究,应用最广泛的是缓冲区增长法[5-6],通过增长弧段的缓冲区来选定多个候选匹配集,然后计算形状、位置和拓扑关系等特征相似度。面要素匹配是依据要素的几何特征和拓扑关系构建综合的相似度评价模型来获得最终的匹配结果。其中几何特征相似度评价的正确性关键在于对面要素形状描述函数的选择,目前已提出的描述方法有几何距法[7]、形状多级描述法[8]及正切空间描述法[9]等。而针对多尺度数据存在几何类型异构的匹配问题(如线-面匹配),则提出了构建面要素内部的TIN三角网,并提取面要素的骨架线与线要素进行匹配的方法[10]。
目前空间匹配的研究主要针对同构要素类型,异构类型是同名地物在不同比例尺的地理表达,实质是以不同程度的制图综合形成复合要素体现的,方式有两种:选取与概括,概括是通过去掉制图物体总体中的细部及类别、等级的合并,更突出地反映物体的基本特征。对于新一轮土地利用调查工作中,多专题、多尺度间复合要素1:N、N:1和M:N的复杂匹配关系研究较少。
本文围绕土地调查实际业务需要,研究土地调查空间要素定量匹配和差异检测技术,从制图综合概括误差角度分析多尺度数据的几何特征差异的原因,提出基于缓冲区膨胀的匹配方法。基本原理是对候选匹配集中的要素进行一次优化,通过对匹配集中的每个目标要素建立缓冲区多边形,并不断膨胀这个多边形,由于缓冲区的作用,弱化同名要素间的尺度细节差异,强化非同名要素间的形状总体差异,同时,也使得所有要素归一化为面要素匹配,然后再针对面-面要素计算圆弧投影形状相似度,得到最终的匹配差异结果。
1 多尺度矢量空间数据概括误差分析制图综合是造成尺度间同名要素差异最大的主观因素[11-12]。制图综合是表达空间数据多尺度概念的重要方法[13]。空间要素的细节层次的表达随着空间表达尺度的差异而改变,细微轮廓特征可以在大比例尺地图中充分地表现出来,可是在小比例尺地图上要表现这些特点,则需要借助制图综合的优势,将其非主要的特征剔除,达到突出主要地物特征的目的[14-15]。这就导致了同名要素可能从原有的同种几何类型匹配转变为不同几何类型间的要素匹配,甚至是混合要素间的匹配问题。本文把这种概括和简化操作给同名要素带来的影响称为概括误差。概括误差会导致要素几何类型、详尽程度和拓扑结构发生变化,具体可以归纳为M:N、N:1、1:N、1:1和1:0(或0:1)5种同名要素映射关系。
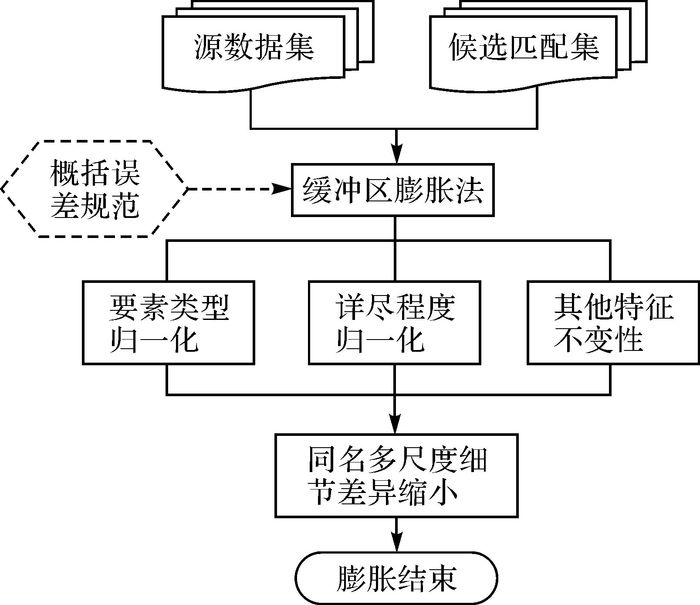
2 缓冲区膨胀法 2.1 基本原理与可行性分析不同比例尺的土地调查数据,描述同名要素在详尽程度、要素类型、精度位置方面都有明显不同。基于概括误差的缓冲区膨胀原理是对各不同尺度同名地物,按其所处尺度的概括误差做缓冲区,归一化到真实场景尺度,弱化了要素的细节特征,突出了要素的主体形态特征,再进行比较匹配,具体如图 1所示。
|
| 图 1 缓冲区膨胀法原理 |
缓冲区膨胀将几何类型不一致的要素匹配问题都归结为面与面的要素匹配。
2.1.2 详尽程度归一化根据缓冲区尖锐角平滑特性可知,采用构建缓冲区的办法可以使得详尽程度高的矢量数据在膨胀过程中得到图形形状简化。而简化的程度应依据不同比例尺的制图规范来调节缓冲半径。另外,就同名要素而言,只需要较小的缓冲半径就可以令两者要素间的差异缩小。反之,如果是非同名要素建立缓冲区,则要求更大的缓冲半径才能符合几何相似度阈值的要求。换言之,缓冲区膨胀法能够提高同名要素的匹配度,增强非同名要素间的形状差异。
2.1.3 其他特征不变性根据缓冲区重心、方向及形态基本不变性原理可以知道尖锐角平滑特性只是提高了同名要素的形状相似度,没有对待匹配要素的其他相似度判断造成影响,因此同名要素的综合几何相似度得到了提高,也保证了缓冲区膨胀法在相似度评价匹配模型中的可行性。
2.2 缓冲区膨胀步骤假设有一源数据集A和目标数据集B。Ai为A中的一个源实体,Ai的候选匹配集表示为Zi={Zi1, Zi2, …, Zin},对Zi进行缓冲区膨胀,并将最终膨胀好的缓冲区多边形结果保存在Zi′={Zi1′, Zi2′, …, Zin′}中。缓冲区膨胀法的具体步骤如下。
2.2.1 缓冲区膨胀半径的阈值设定判断Ai是否为点实体,如果是,则令Zi直接作为最终膨胀结果Zi′=Zi1′, Zi2′, …, Zin′保存起来。反之,Ai可根据距离d1建立缓冲区Ai′,然后对Zi中的每个候选匹配实体Zij(j=1, 2, …, n)进行缓冲区膨胀,起始缓冲半径为d2,缓冲半径阈值为dMAX,缓冲半径每次膨胀的距离为d′,通过式(1)得到初始缓冲区膨胀多边形集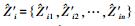
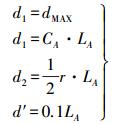 (1)
(1) 式中,CA为《国家基本比例尺地图汇编规范》中源数据集A在当前比例尺下允许的最大概括误差;LA为源数据集A的实际距离;r为下节中设定的候选集缓冲半径。采用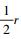
平移Ai′,使得Ai′的重心与Zij′的重心重合,计算每个Zij′与Ai′的初始面积重叠相似度。其中面积重叠相似度计算为
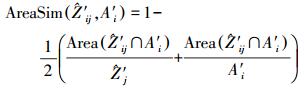 (2)
(2) 首先判断面积重叠相似度与前次相比是否提高(首次比较时视为面积重叠相似度有所提高)。如果没有,则将前一次膨胀的多边形结果Zij′作为最终的缓冲区多边形保存到Zi′中,候选匹配实体Zij膨胀结束。反之,如果有所提高,那么在保证缓冲半径d<dMAX的前提下,在当前的缓冲半径基础上不断增加d′距离,并按照增长后的缓冲半径重新对候选匹配实体Zij进行缓冲区膨胀,直至面积重叠相似度达到最大值为止。最后将膨胀好的多边形结果Zij′作为最终的缓冲区多边形保存到Zi′中。
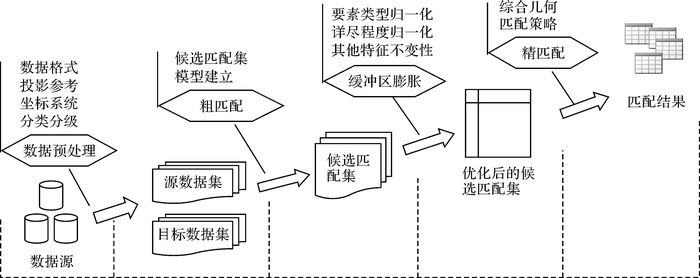
3 基于缓冲区膨胀的多尺度矢量空间数据匹配模型基于缓冲区膨胀的多尺度矢量空间数据匹配模型如图 2所示。
|
| 图 2 匹配模型 |
首先利用源实体建立缓冲区,将目标实体与刚建立的缓冲区进行叠加分析,令位于缓冲区内的目标实体集作为源实体的候选匹配集。该方法能够在一定程度上消除由于投影误差和精度误差造成候选匹配集不完整的可能性。缓冲区的半径r一般按照两个数据集的点位精度来确定
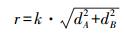 (3)
(3) 式中,dA、dB分别为源数据集A和目标数据集B的点位精度;k表示倍数,一般取2或3。
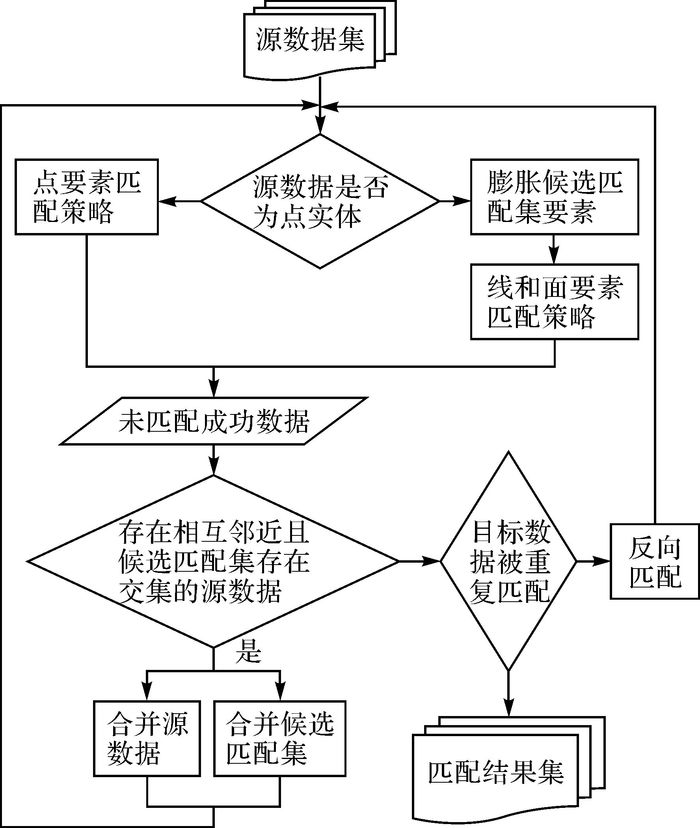
3.2 精匹配几何匹配是矢量空间数据匹配的主要研究方向,结合语义和拓扑匹配来提高匹配精度。依据矢量要素的几何特征,按照一定的匹配模型来对同名要素进行比对,从而得到最终的匹配结果,具体如图 3所示。本文采用计算两个要素间多个特征相似度的加权平均值的方式来获得实体的综合相似度。
|
| 图 3 归一化空间要素综合几何匹配策略 |
设待匹配要素Ai、Zij共有n个几何特征,第i个几何特征的相似度值为σi,权重为ωi,其中i=1, 2, …, n,那么要素Ai、Zij的综合相似度为
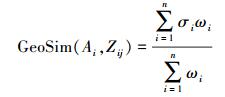 (4)
(4) 式中,ωi的取值由专家经验来确定,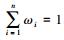
本文提出一种基于圆弧投影的空间形状相似度衡量指标。原理是将两个待匹配要素的边界坐标投影到同一个外包络圆周上,用两要素随角度变化的差异描述函数考量要素差异的定位定量指标。
设有一面要素A,圆O为面要素A的外包络圆,记外包络圆的半径为r。从圆心出发,以平行于横轴且与横轴同方向的半径射线为起始边,θ为间隔角度,逆时针旋转射线,那么多边形A将按角度θ剖分成k个等分,k=2π/θ。计算多边形上的每个等分点Pi投影到外包络圆上的投影长度记为li,如图 4(a)所示。令角度θ为自变量,投影长度l为因变量,可以描述出多边形A的形状函数为lA(θ)。其中,定义域θ∈(0, 360],值域l∈[0, r)。分别用360和r对θ和l进行归一化处理,使得要素形状描述满足缩放不变性。图 4(b)是图 4(a)lA(θ)绘制出的曲线。

|
| 图 4 圆弧投影差异描述函数 |
将待匹配要素A、B的圆弧投影形状函数表示为lA(θ)、lB(θ)。计算当横坐标取相同值时,lA(θ)、lB(θ)所对应的纵坐标的差值序列f,并且求f的平均值μf,则要素A、B的形状相似度为
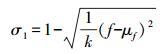 (5)
(5) 重心距离指标(σ2)及多边形方向指标(σ3)是经典的传统相似度匹配指标,这里不再累述。
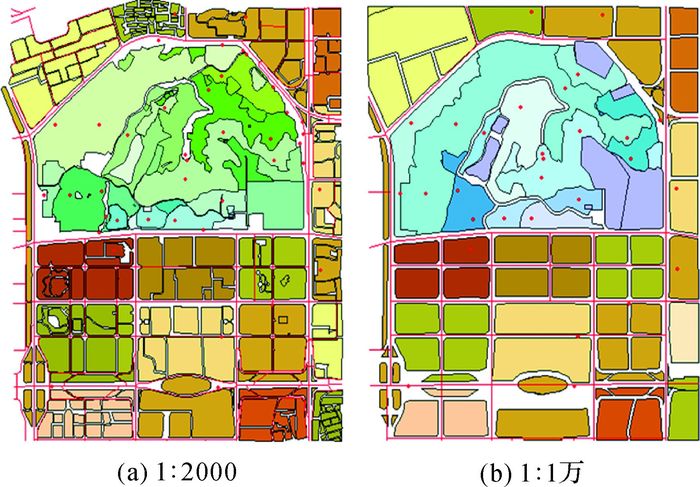
4 试验与质量评价 4.1 试验数据介绍按照新一轮土地利用调查城镇区域的技术要求,选取某市部分2006年1:2000(如图 5(a)所示)和2005年1:10 000(如图 5(b)所示)土地利用调查数据进行匹配试验,包含了植被、居民地、道路等要素。
|
| 图 5 居民地匹配数据 |
首先,将1:1万数据作为源数据集,1:2000数据作为目标数据集,采用高斯-克吕格投影到单位为米的平面直角坐标系,然后,令源数据集的缓冲区半径为
在目标数据集中搜索每个要素的候选匹配集,对面要素候选匹配集作缓冲区膨胀,同时对源要素也作缓冲区膨胀,根据1:10 000地图汇编规范,其允许的最小点位误差为0.1 mm,最大概括误差为0.6 mm,所以令d1=6 m、d2=1.4 m、d′=1 m、dMAX=6 m,再按照前文的匹配策略进行匹配,其中权值分别定为ω1=0.4、ω2=0.3、ω3=0.3,匹配阈值为0.8。居民点实际匹配情况见表 1。传统匹配方法是指在获得要素候选匹配集后直接进行综合几何相似度匹配,结果见表 2。缓冲区膨胀法匹配结果见表 3。
| 匹配类型 (1:1万—1:2000) | 匹配情况 | 源数据匹配个数 (1:1万) | 目标数据匹配个数 (1:2千) | 源数据不匹配个数 (1:1万) | 目标数据不匹配个数 (1:2千) |
| 面—面 | 1:1 | 21 | 21 | 0 | 8 |
| M:N | 82 | 199 |
| 匹配类型(1:1万 —1:2000) | 匹配 情况 | 实际匹配 个数 | 实际不 匹配个数 | 匹配 个数 | 不匹配 个数 | 正确匹配 个数 | 错误匹配 个数 | 假匹配 个数 | 正确不 匹配个数 | 假不匹配 个数 |
| 面—面 | 1:1 M:N | 21 82 | 0 | 19 73 | 11 | 19 59 | 0 14 | 0 0 | 0 | 11 |
| 综合 | 查准率=86.00% 查全率=90.09% 速度=69个/s | |||||||||
| 匹配类型(1:1万 —1:2000) | 匹配 情况 | 实际匹配 个数 | 实际不 匹配个数 | 匹配 个数 | 不匹配 个数 | 正确匹配 个数 | 错误匹配 个数 | 假匹配 个数 | 正确不 匹配个数 | 假不匹配 个数 |
| 面—面 | 1:1 M:N | 21 82 | 0 | 21 81 | 1 | 21 76 | 0 5 | 0 0 | 0 | 1 |
| 综合 | 查准率=95.45% 查全率=97.30% 速度=61个/s | |||||||||
尺度间居民地要素M:N匹配关系是居民地匹配的重点和难点。缓冲区膨胀法在查全率方面提高了7.21%,匹配精度方面提高了9.45%,说明该方法在M:N情况中的多尺度居民地匹配中有很好的适用性。
5 结语根据新一轮土地利用现状调查的工作要求,本文研究了复合要素空间差异的定量判别技术,引入制图综合工作中概括误差概念,通过缓冲区膨胀解决多尺度复合要素尺度归一到实地的问题,提出了一种圆弧投影的空间形状相似度定量检测方法,并综合重心距离法和多边形方向法,实现了尺度间复合要素差异的快速定量检测。在验证试验中,对城市打开前后,1:10 000(2005年)和1:2000(2006年)的同区域数据作空间匹配试验,进行精度评价,采用基于缓冲区膨胀的尺度间综合匹配方法完成了土地调查复合要素空间差异的定量判别。试验结果表明,在与传统方法速度相当的情况下,该方法在查全率与匹配精度方面有很大提高,能够充分满足新一轮土地调查数据差异检测工作的需要。
| [1] | 郭黎. 多源地理空间矢量数据融合理论与方法研究[D]. 郑州: 信息工程大学, 2008. |
| [2] | 童小华, 邓愫愫, 史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2): 210–217. |
| [3] | BEERI C, DOYTSHER Y, KANZA Y, et al.Finding Corresponding Objects when Integrating Several Geo-spatial Datasets[C]//Proceedings of the 13th Annual ACM International Workshop on Geographic Information Systems. Bremen:ACM, 2005:87-96. |
| [4] | 李爱国, 胡圣武. 基于直觉模糊集多属性决策的空间数据质量评价的研究[J]. 测绘通报, 2014(3): 46–50. |
| [5] | 赵彬彬, 邓敏, 徐震, 等. 多尺度地图面目标匹配的统一规则研究[J]. 武汉大学学报(信息科学版), 2011, 36(8): 991–994. |
| [6] | 徐枫, 邓敏, 赵彬彬, 等. 空间目标匹配方法的应用分析[J]. 地球信息科学学报, 2009, 11(5): 657–663. |
| [7] | 赵东保, 盛业华, 张卡. 利用几何矩和叠置分析进行多尺度面要素自动匹配[J]. 武汉大学学报(信息科学版), 2011, 36(11): 1371–1375. |
| [8] | 安晓亚, 孙群, 肖强, 等. 一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用[J]. 测绘学报, 2011, 40(4): 495–501. |
| [9] | FILIN S, DOYTSHER Y. The Detection of Corresponding Objects in a Linear-based Map Conflation[J]. Surveying and Land Information Systems, 2000, 60(2): 117–128. |
| [10] | 刘闯, 钱海忠, 王骁, 等. 利用城市骨架线网的道路和居民地联动匹配方法[J]. 测绘学报, 2016, 45(12): 1485–1494. DOI:10.11947/j.AGCS.2016.20160221 |
| [11] | 王家耀, 钱海忠. 制图综合知识及其应用[J]. 武汉大学学报(信息科学版), 2006, 31(5): 382–386. |
| [12] | 钱海忠, 武芳, 郭健, 等. 基于制图综合知识的空间数据检查[J]. 测绘学报, 2006, 35(2): 184–190. |
| [13] | 王家耀, 邓红艳. 基于遗传算法的制图综合模型研究[J]. 武汉大学学报(信息科学版), 2005, 30(7): 565–569. |
| [14] | 章莉萍, 郭庆胜, 孙艳. 相邻比例尺地形图之间居民地要素匹配方法研究[J]. 武汉大学学报(信息科学版), 2008, 33(6): 604–607. |
| [15] | 胡云岗, 陈军, 赵仁亮, 等. 地图数据缩编更新中道路数据匹配方法[J]. 武汉大学学报(信息科学版), 2010, 35(4): 451–456. |