2. 武汉大学中国南极 测绘研究中心, 湖北 武汉 430079
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China
早期人们普遍假设GPS坐标时间序列为独立分布,即只有白噪声(white noise,WN)。近年来,许多研究表明除白噪声外,有色噪声也广泛存在于各种连续GPS站坐标时间序列,如闪烁噪声(flicker noise,FN)和随机游走噪声(random walk noise,RWN)等。Williams使用最大似然估计法(MLE)分析了9种全球GPS解的坐标时间序列噪声特性,发现其最优噪声模型为白噪声+闪烁噪声[1]。蒋志浩等采用功率谱分析方法和最大似然法估计了CGCS2000框架下国家CORS网坐标时间序列的噪声特性,发现白噪声+闪烁噪声+随机游走噪声是该GPS网络的最优噪声模型[2]。姜卫平等对澳大利亚板块10个连续GPS测站1998—2009年坐标时间序列的噪声特性进行了分析,发现这些坐标时间序列水平分量的最优噪声模型为白噪声+闪烁噪声[3]。上述研究表明,各区域适用的噪声模型主要包括白噪声和两种有色噪声(FN和RWN)。
东南极区域大部分被厚重冰盖所覆盖,仅在沿海区域存在少数测站,是国际上地球动力学研究的重点区域之一。近年来,随着气候变暖的影响,南极一些冰川在加速融化,损失的质量往往会引起地表的黏弹性形变,获取精确的三维地壳形变速度,对于气候学、冰川学、地球动力学等领域的研究都具有非常重要的意义[4-6]。目前长期连续GPS观测已经可以监测这些微小形变,对GPS测站坐标时间序列噪声特性进行研究,有利于改善GPS测站速度估计的精度[7-8]。本文收集了东南极区域6个连续GPS测站长期观测数据,通过处理和分析来研究两种有色噪声(WN和RWN)对测站坐标时间序列参数估计的影响。
1 噪声分析方法白噪声是一种随机过程或信号,其功率谱密度在全部频域内都是均匀分布的,而其他不具备这一特性的噪声统称为有色噪声。如果坐标时间序列中存在有色噪声,那么随着观测次数的增加,参数估计值的方差不再随之变小。在利用GPS重复观测估计测站速度时,假设只考虑白噪声而不考虑有色噪声的影响,就会导致速度值方差的估计过于乐观,并不能反映实际的精度[9]。
目前,用于坐标时间序列噪声估计的方法主要有:最大似然估计方法[10]、频谱估计方法[11]和经验估计方法[12-13]等。本文采用的噪声分析方法为最大似然估计法,其基本思想为:对于给定的一系列观测量x,必须使这些值发生的概率(l,也称似然)最大。假定存在一个高斯分布,其似然l为
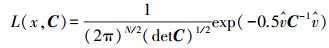 (1)
(1) 式中,det为一个矩阵的行列式;C为假设噪声的协方差矩阵,每种噪声均使用一个特定的协方差矩阵来表示;N为历元数,是使用相同协方差矩阵C并利用加权最小二乘方法对线性函数拟合后的残差。对式(1)两边求对数,并使其对数似然最大,即
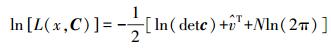 (2)
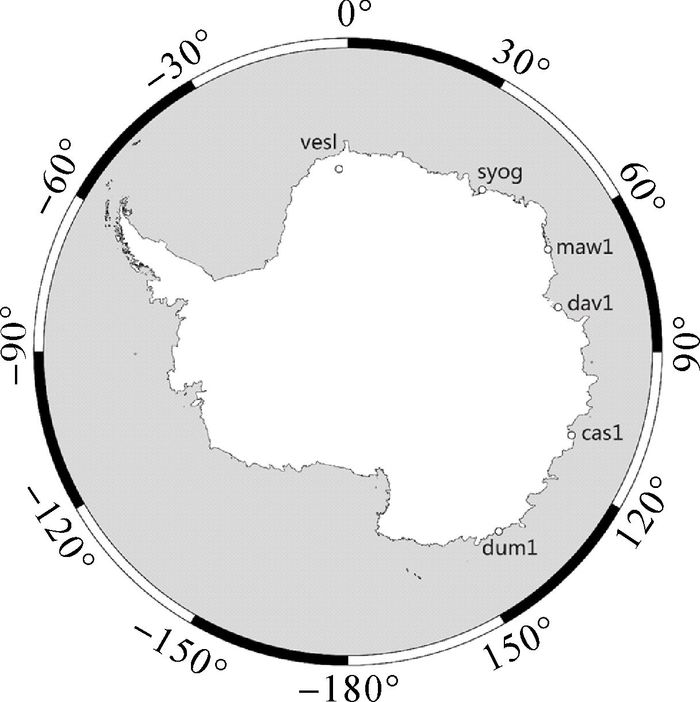
(2) 本文选取了东南极沿海区域6个GPS测站(CAS1、DAV1、DUM1、MAW1、SYOG、VESL,如图 1所示),均为连续观测的IGS站,数据跨度为2005—2014年,原始数据可以从SOPAC(Scripps Orbit and Permanent Array Center)数据库下载。
|
| 图 1 东南极区域GPS测站分布 |
GAMIT/GLOBK 10.5是一个高精度GNSS综合分析软件集,可用来估计测站坐标和速度、震后变形的随机函数、大气延迟、卫星轨道及地球定向参数等。本文使用该软件对GPS原始数据进行基线解算,基线解算的策略见表 1。
| 选项 | 策略 |
| 解算模式 | RELAX |
| 观测值类型 | LC_AUTCLN |
| 基准站约束/m | 0.05、0.05、0.10 |
| 其他站约束/m | 100、100、100 |
| 截止高度角/(°) | 15 |
| 历元间隔/s | 30 |
| 对流层模型 | Saastamoinen |
| 潮汐模型 | FES2004 |
| 光压模型 | BERNE |
| 参考框架 | ITRF2008 |
基线处理后,本文使用GLOBK软件将基线解在ITRF2008框架下进行网平差。为了维持区域GPS网络框架的稳定性,本文平差时加入了全球IGS网络1996—2014年igs1—igs9共计9个子网的基线解算结果(由SOPAC提供下载,链接为:ftp://garner.ucsd.edu/archive/garner/solutions/global/),与IGS全球网基线解算结果进行联合平差。部分GPS测站时间序列由于天线变化或地震发生阶跃,对阶跃前后的坐标时间序列分段拟合,求出阶跃前后的坐标拟合差(即阶跃值),然后对阶跃后的测站坐标进行改正。平差后各测站坐标时间序列水平方向的加权均方根误差均小于5 mm,垂向的加权均方根误差均小于10 mm。
2.4 异常值剔除由于外界环境变化或内部元件的变化等因素,网平差得到的测站时间序列具有少量异常值,对分析结果影响很大,应予以剔除[14]。本文使用3倍四分位数差法则(interquartile range,IQR)[15]来剔除坐标时间序列中的异常值,公式如下
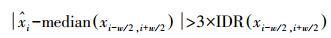 (3)
(3) 式中,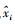
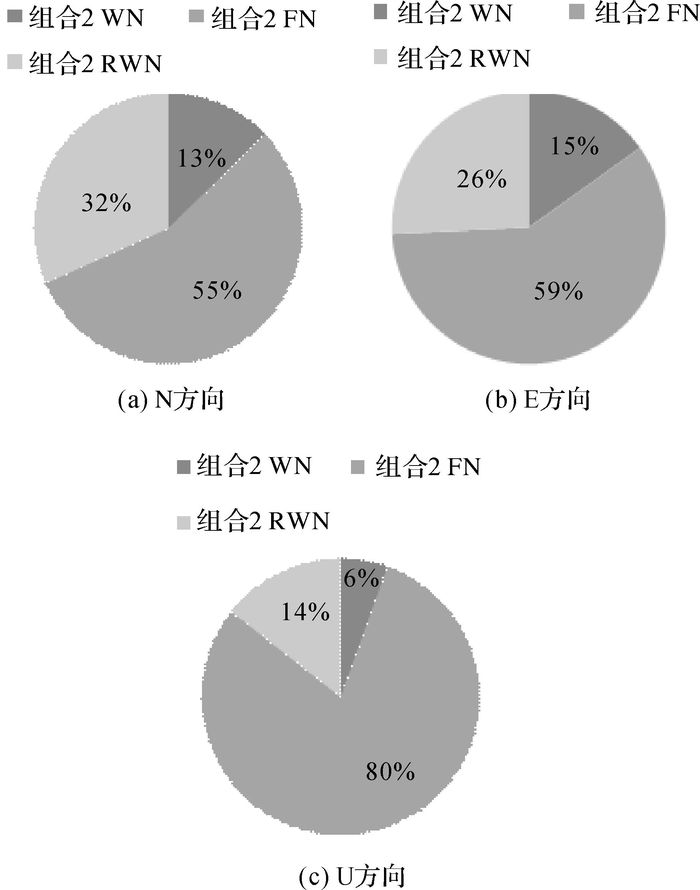
为了研究有色噪声对GPS测站三维速度估计的影响,本文假设两种噪声组合,第一种仅包含白噪声,第二种为白噪声+闪烁噪声+随机游走噪声的组合。本文利用这两种假设噪声组合分别估计了GPS测站坐标时间序列的3种噪声量级(见表 2)。由表 2可知,组合1中所有站点都存在白噪声,而组合2中所有站点都存在白噪声和闪烁噪声,部分测站如CAS1、DAV1、DUM1还存在随机游走噪声,特别是DUM1的N、E、U这3个方向的坐标时间序列中都存在较大量级的随机游走噪声。图 2给出了噪声组合2中3种噪声平均量级占总平均噪声量级的百分比,可以看出在N、E、U这3个方向上闪烁噪声都占据了主导地位,其次是随机游走噪声,白噪声占比最小。组合2的白噪声量级小于组合1,但是组合2的闪烁噪声量级远远大于白噪声量级,对于DUM1测站,随机游走噪声量级不可忽视,表明在进行时间序列参数估计时不考虑有色噪声会高估白噪声的真实量级,同时大大低估坐标时间序列中的总噪声。对于同种噪声,N、E方向的噪声量级十分相近,U方向的噪声量级除组合2白噪声外,都比N、E方向大。组合2白噪声量级在N、E、U这3个方向上基本一致,说明真实的白噪声对N、E、U这3个方向的影响大小一致。
| mm | ||||||
| 测站 | 分量 | 组合1 | 组合2 | |||
| WN | WN | FN | RWN | |||
| CAS1 | N方向 | 2.13 | 1.01 | 4.88 | 0.00 | |
| E方向 | 2.47 | 1.51 | 4.54 | 1.27 | ||
| U方向 | 8.15 | 1.28 | 21.00 | 0.00 | ||
| DAV1 | N方向 | 3.02 | 1.11 | 4.19 | 4.26 | |
| E方向 | 2.17 | 1.44 | 4.73 | 0.00 | ||
| U方向 | 8.62 | 1.54 | 19.61 | 5.03 | ||
| DUM1 | N方向 | 3.36 | 1.05 | 5.09 | 13.14 | |
| E方向 | 3.92 | 0.99 | 6.99 | 12.87 | ||
| U方向 | 8.67 | 1.44 | 21.42 | 17.24 | ||
| MAW1 | N方向 | 2.11 | 1.21 | 4.95 | 0.00 | |
| E方向 | 2.38 | 1.62 | 4.91 | 0.00 | ||
| U方向 | 6.46 | 1.67 | 18.77 | 0.00 | ||
| SYOG | N方向 | 2.34 | 1.35 | 5.68 | 0.00 | |
| E方向 | 2.64 | 1.38 | 6.15 | 0.00 | ||
| U方向 | 7.25 | 1.27 | 20.39 | 0.00 | ||
| VESL | N方向 | 2.36 | 1.32 | 5.81 | 0.00 | |
| E方向 | 2.11 | 1.34 | 5.05 | 0.00 | ||
| U方向 | 7.25 | 1.29 | 22.37 | 0.00 | ||
|
| 图 2 N、E、U这3个方向噪声组合2中各噪声平均量级占总平均噪声量级的百分比 |
坐标时间序列的参数估计主要包括三维速度、周期、振幅等,本文在比较不同噪声组合对参数估计影响时,以速度为例进行分析,见表 3。两种噪声组合条件下的速度估计值之间差别较小,U方向差别大于N、E方向,N、E、U方向的最大差别量级为-0.32、-0.31、0.84 mm/a,而且利用噪声组合2估计的速度误差要大于组合1,说明是否考虑有色噪声对于速度估计值的影响较小,对U方向的影响大于N、E方向,但是不考虑有色噪声会大大低估速度估计的真实不确定性,给误差定量分析带来困难。因此,在进行测站三维速度估计时,应考虑有色噪声对其的影响。
| mm/a | ||||
| 测站 | 噪声组合 | VN | VE | VU |
| CAS1 | 组合1 | -9.32±0.01 | 1.08±0.01 | 2.56±0.05 |
| 组合2 | -9.39±0.16 | 1.38±0.44 | 2.58±0.66 | |
| DAV1 | 组合1 | -5.18±0.02 | -3.47±0.01 | 2.59±0.05 |
| 组合2 | -5.37±1.35 | -3.38±0.15 | 1.80±1.73 | |
| DUM1 | 组合1 | -12.24±0.02 | 7.81±0.02 | 0.09±0.05 |
| 组合2 | -11.91±4.14 | 7.80±4.06 | -0.75±5.49 | |
| MAW1 | 组合1 | -2.00±0.01 | -4.02±0.01 | -0.18±0.04 |
| 组合2 | -2.12±0.16 | -3.92±0.16 | -0.36±0.59 | |
| SYOG | 组合1 | 2.93±0.01 | -4.03±0.02 | 0.31±0.04 |
| 组合2 | 2.79±0.18 | -3.90±0.20 | 0.24±0.64 | |
| VESL | 组合1 | 10.37±0.02 | -0.50±0.02 | -0.06±0.07 |
| 组合2 | 10.34±0.23 | -0.37±0.20 | 0.15±0.89 | |
本文采用GAMIT/GLOBK10.5软件对东南极区域6个连续GPS测站2005—2014年的实测数据进行了解算和平差,并利用最大似然法(MLE)分别估计了在两种假设噪声模型条件下的测站三维运动速度及其不确定性,结果表明:
(1) 白噪声和闪烁噪声广泛存在于东南极区域的坐标时间序列中,随机游走噪声仅存在于少数测站(如DUM1)的坐标时间序列,而且闪烁噪声的量级普遍大于随机游走噪声和白噪声。
(2) 考虑两种有色噪声(FN和RWN)对东南极区域GPS测站速度估计量级的影响不大,水平方向最大约为0.3 mm/a,垂直方向最大约为0.8 mm/a。
(3) 不考虑有色噪声会大大低估东南极测站速度估计的真实不确定性,给误差定量分析带来了困难,因此在进行测站坐标时间序列参数估计时,应考虑有色噪声的影响。
| [1] | WILLIAMS S D P, BOCK Y, FANG P, et al. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 2004, 109(B3): 1–19. |
| [2] | 蒋志浩, 张鹏, 秘金钟, 等. 顾及有色噪声影响的CGCS 2000下我国CORS站速度估计[J]. 测绘学报, 2010, 39(4): 355–363. |
| [3] | 姜卫平, 周晓慧. 澳大利亚GPS坐标时间序列跨度对噪声模型建立的影响分析[J]. 中国科学:地球科学, 2014, 44(11): 2461–2478. |
| [4] | 贾路路, 相龙伟, 雒燕飞. 利用空间大地测量观测数据研究北美陆地水储量变化[J]. 测绘通报, 2014(8): 6–9. |
| [5] | 李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496–503. |
| [6] | 吴伟伟, 孟国杰, 伍吉仓. 华北地区GPS基准站坐标时间序列噪声特征研究[J]. 大地测量与地球动力学, 2016, 36(8): 708–713. |
| [7] | 田云锋, 沈正康, 李鹏. 连续GPS观测中的相关噪声分析[J]. 地震学报, 2010, 32(6): 696–704. |
| [8] | 杨登科, 安向东, 黄广利, 等. 不同GPS时间序列跨度对噪声模型建立的影响[J]. 测绘科学, 2016, 41(5): 33–37. |
| [9] | 李斐, 马超, 张胜凯, 等. 南极半岛地区GPS坐标时间序列噪声分析及形变模式初探[J]. 地球物理学报, 2016, 59(7): 2402–2412. DOI:10.6038/cjg20160707 |
| [10] | JOHNSON H. Correlated Errors in Geodetic Time Series:Implications for Time-dependent Deformation[J]. Journal of Geophysical Research, 1997, 102(B1): 591–603. DOI:10.1029/96JB02945 |
| [11] | BERAN J. On Parameter Estimation for Locally Stationary Long-memory Processes[J]. Journal of Statistical Planning & Inference, 2009, 139(3): 900–915. |
| [12] | WILLIAMS S D P. The Effect of Coloured Noise on the Uncertainties of Rates Estimated from Geodetic Time Series[J]. Journal of Geodesy, 2003, 76(9-10): 483–494. DOI:10.1007/s00190-002-0283-4 |
| [13] | 张恒璟, 程鹏飞. 基于经验模式分解的滤波去噪方法研究进展[J]. 测绘通报, 2014(2): 1–4. |
| [14] | 黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31–33. |
| [15] | NIKOLAIDIS R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[J]. Cancer Research, 2002, 71(8 Supplement): 714–714. |



