2. 甘肃省地理国情监测工程实验室, 甘肃 兰州 730070;
3. 中国测绘科学研究院, 北京 100039;
4. 中国地震局第二监测中心, 陕西 西安 710054
2. Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou 730070, China;
3. Chinese Academy of Surveying and Mapping, Beijing 100039, China;
4. The Second Monitoring and Application Center, CEA, Xi'an 710054, China
流动重力是一种相对重力,是某一固定测点在一定周期内重力重复观测之差[1]。作为地震监测的重要数据之一,流动重力的观测备受关注。自20世纪60年代我国开展地震监测工作以来,陆续在主要构造带和地震危险区建立了由3000多个观测点组成的重力监测网[2],这些成果为流动重力在中国地震系统监测中的应用奠定了坚实的地位[3]。尽管重力测站已经足够多,但要获取流动重力的空间分布特征,掌握流动重力更为详细的信息,仍需要对其进行插值;此外,个别测站可能受人为或自然因素的影响,致使数据缺失,要获取这个区域内的流动重力,较为可靠的方法也是插值。目前,在二维离散点数据插值方面,没有固定统一的插值方法,比较常用的有:Kriging法、反距离加权法、Shepard法及趋势面法等。
对于重力数据的插值,学者们作了一定的研究:徐遵义等利用改进的Shepard算法对重力数据进行了插值,结果表明该算法可减小插值误差[4];吴太旗等利用Kriging法、改进的二次曲面Shepard法和径向基函数法对海洋重力数据进行了插值研究,得出Kriging插值速度优于其他两种插值法,但精度稍低于其他两种插值法[5];彭泽辉等利用最小二乘配置法对重力变化数据进行了格网化,取得了较好的结果,并与其他插值法(如Kriging等)进行了比较[6];李振海等比较了重力数据格网化的方法,得出格网化的结果与数据分布有较大关系,同一数据插值,Kriging插值效果最好,但其计算速度较慢[7];孙文等使用Kriging、CoKriging、Shepard法对高精度重力数据进行格网化插值比较,得出了与李振海相似的结论[8]。总结这些研究成果,可以发现在重力数据插值方面,Kriging法、Shepard法、反距离加权法效果较好。然而,对于流动重力的获取,需要进行仪器误差改正、固体潮改正、大气改正、格值改正、零漂改正及相应的平差处理等诸多环节[2, 9],因此,对其插值还需要在重力插值方法的基础上作进一步研究。一般的,插值结果要求能反映区域的总体特征,受地球内部随机性分布的密度异常等因素的影响,简单的数学插值方法有时不能准确地反映地球重力场的特性,而且流动重力监测网测点的分布情况以及数据解算过程中的数学方法对插值效果影响较大,寻求更加适合流动重力变化特性的插值方法是流动重力插值中的重要内容。本文选取对重力数据插值效果较好的Kriging法、反距离加权法、改进的Shepard法对流动重力数据进行插值,从数据分布、插值点个数、插值分辨率等方面对比分析这3种插值方法的插值效果,以期得到最佳的插值方法。
1 插值方法基本原理 1.1 Kriging法[10-11]Kriging法由南非矿山工程师Krige提出,法国地理数学家Matheron对其进行了推广和完善。普通Kriging是地理、测绘等学科使用最为广泛的插值方法。设Z为待插值点,Zi为第i个样本的实测值,实测样本数为m,λi为第i个样本的权重系数,则Kriging法的数学表达式为
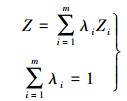 (1)
(1) 计算中λi需要保证Z为无偏估计,且估计方差σ2小于观测值的其他线性组合产生的方差,式(2)为Z的最小方差表达式。要确保σ2最小,则对于∀j,均存在式(3)。
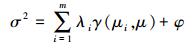 (2)
(2) 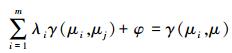 (3)
(3) 式中,γ(μi, μj)和γ(μi, μ)分别为第i个样本点和第j个样本点、第i个样本点和待插值点的半方差;φ为拉格朗日因子。
半方差函数是插值数据空间结构的描述,也是Kriging插值计算过程中最重要的部分。常见的半方差函数有球面模型、指数模型、高斯模型、线性模型。本文插值过程中使用球面模型进行半方差计算,利用式(2)、式(3)计算每个点的权重系数及拉格朗日因子,进而通过式(1)求取插值点的估算值。
1.2 反距离加权法反距离加权是最常用的空间插值法之一,由美国国家气象组于1972年首次提出[10]。该方法易于计算,便于理解,在样本点分布均匀的情况下能得到较好的插值结果,其核心是根据插值点与样本点之间的距离赋予插值权重,距离插值点越近的样本点权重值越大[12]。设Z为待插值点,Zi为第i个样本的实测值,实测样本数为m,di为第i个样本点与插值点之间的距离,n为幂指数(距离反比平方中n=2),则距离反比插值的数学表达式可写为
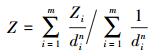 (4)
(4) Shepard法既适合局部插值又可用于整体插值,广泛应用于GIS、生命科学、机械工程等学科[4]。最初的Shepard法存在一些问题,如当样本点过多,计算耗时;权函数确定仅依赖于距离等。经过学者们对其不断的修正、改进,目前所使用的改进Shepard法能得到对数据有较好平滑效果的权函数,能极大地减小插值结果中的“牛眼”现象。改进的Shepard法其实质是距离倒数加权的最小二乘法[5]。设Z为待插值点,Zi为第i个样本值,实测样本数为m,ρ(ri)为第i个样本的权重系数,ri为插值点与第i个样本点之间的欧氏距离,则改进Shepard法的数学表达式可以表示为[13-14]
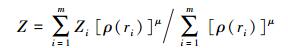 (5)
(5) 当ri为0时,插值点的值等于第i样本点,一般μ取2[4]。ρ(ri)通过下式计算
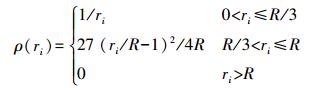 (6)
(6) 式中,R为以插值点为圆心的搜索半径。
2 试验及结果分析 2.1 试验数据及插值方法参数设定本文选取陕西省关中地区观测点流动重力解算值进行插值研究,数据来源于陕西省测绘地理信息局,数据的时间尺度为2009—2014年(每年1月与6月各一期数据),空间尺度为106.5°—111°E,33.5°—36°N。
由于解算过程中对一些错误数据的舍去以及某些测站某期没有测得数据,使得每一期的流动重力数据数量不一致,空间分布也不相同,因此,本文仅在试验中给出各期流动重力测点(样本点)的空间分布图。
为便于插值研究,对原始数据进行简单的预处理,以2011年1月为基准,对所有数据进行基准扣除,得到第1组待插值的9期数据;以2011年6月为基准,对所有数据进行基准扣除,得到第2组待插值的9期数据。
对各类方法分别设置不同的参数,以期得到较为理想的插值方法,为下文制图和描述的方便,文中对各类插值方法进行编码,表 1为具体的参数设置。
| 插值方法 | 插值格网 分辨率/(′) | 搜索半 径/(′) | 搜索点 数/(个) | 插值方 法代码 |
| 普通Kriging法 (球面函数) | 2 | — | 9 | I1 |
| 5 | — | 12 | I2 | |
| 反距离加权法 | 2 | 5 | — | I3 |
| 5 | 15 | — | I4 | |
| 30 | — | I5 | ||
| 改进的 Shepard法 | 2 | 15 | — | I6 |
| 5 | 30 | — | I7 |
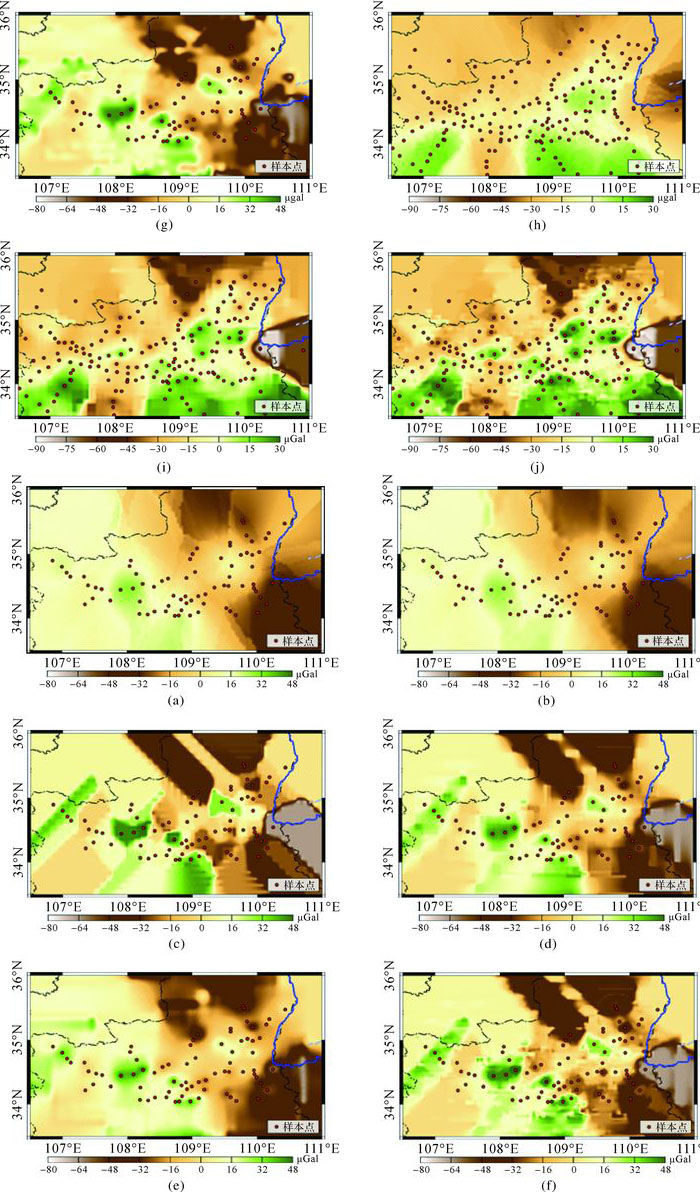
本文使用的插值函数库为中国测绘科学研究院大地测量与地球动力研究所地球重力与垂直基准研究课题组开发,已申报专利。在现有函数库的基础上,实现3种插值方法的批量计算及插值反算(利用插值结果反算插值点的值,下文简称反插)程序设计。对18期数据分别进行插值,共得到每期数据的7种插值结果。以第1组数据2012年6月的插值结果与第2组数据同期2′分辨率插值结果为例进行结果展示,如图 1所示。
|
| 图 1 插值结果展示 |
从图 1(b)、(e)、(g)可以看出,在相同的空间尺度下5′分辨率插值结果过于平滑,根据流动重力数据最主要的用途,其插值结果需要反映局部的一些变化特征,过于平滑的结果不能反映区域异常,相比较,2′的插值结果(如图 1(a)、(c)、(d)、(f)、(h)、(i)、(j)所示)细部特征明显,局部异常得到了较好的体现。就2′分辨率插值结果而言,在区域细节表达方面,改进的Shepard插值结果(如图 1(f)、(j)所示)明显优于球面Kriging插值结果,与距离反比平方插值结果较为接近;球面Kriging插值结果(如图 1(a)、(h)所示)呈现点状向外扩散特征,其总体插值结果整体性较强,这种辐射特征更适于大气、降水[15-16]等一些区域性明显的数据插值,可以看出,其插值过程中丢失了局部极大值和极小值信息,结果整体偏小,而重力数据离散性较强,因此,该方法对流动重力的插值结果不太理想,只有当样本中不存在异常值时,能获得连续性好、平滑程度高的插值结果;反距离加权法的插值结果(如图 1(c)、(d)、(i)所示)15′搜索半径优于5′,5′搜索半径不仅在插值过程中需要大量的迭代才能完成整个区域计算,而且插值结果局部“牛眼”效应较为严重,因此可以确定插值过程中搜索范围不是越小越好,而应该根据样本点个数,对插值范围做相应的调整。整体上,在插值范围内插值分布越均匀,插值结果越好。
对于地球要素插值,某一插值方法的结果精度主要取决于其对要素空间变异性与空间相关性的反应[17],因而插值过程中需要充分考虑数据的地理特性。重力数据反映了地球物理特征,不同于大气、降水数据,具有高频特性,与位置有很大关系。地球重力向量是地球引力和离心力的合力[9, 18],而引力与质点间距离平方成反比,离心力与地球半径成反比,因此插值过程中利用反距离加权解算未知点更能吻合真实值。此外,流动重力的解算过程中使用了最小二乘法进行结果配权,因此,使用改进的Shepard法对流动重力插值,结果的准确度相对较高。
2.3 结果验证为验证各种插值结果的准确度,本文利用插值结果反插样本点,计算反插结果与真值的差值,并分别进行统计。对应前文中结果,表 2给出其对应的统计结果。
| 组别 | 插值方法 | 样本点个数 | 均值 | 标准差 | 最小值 | 最大值 |
| 第1组 | I1 | 75 | -0.749 3 | 14.659 1 | -30.990 0 | 33.710 0 |
| I2 | 75 | -0.826 1 | 15.998 6 | -34.980 0 | 36.300 0 | |
| I3 | 75 | -0.012 0 | 2.944 4 | -10.842 7 | 11.230 5 | |
| I4 | 75 | -0.028 2 | 4.065 7 | -13.358 8 | 12.576 9 | |
| I5 | 75 | -0.634 5 | 9.322 6 | -21.532 8 | 20.867 8 | |
| I6 | 75 | 0.009 5 | 2.101 6 | -8.418 1 | 8.391 3 | |
| I7 | 75 | -0.422 5 | 6.297 1 | -19.650 2 | 12.074 8 | |
| 第2组 | I1 | 183 | 1.787 3 | 18.345 8 | -65.230 0 | 65.890 0 |
| I4 | 183 | 0.049 3 | 3.691 4 | -10.058 6 | 13.864 7 | |
| I6 | 183 | -0.013 2 | 2.256 7 | -8.932 6 | 8.455 0 |
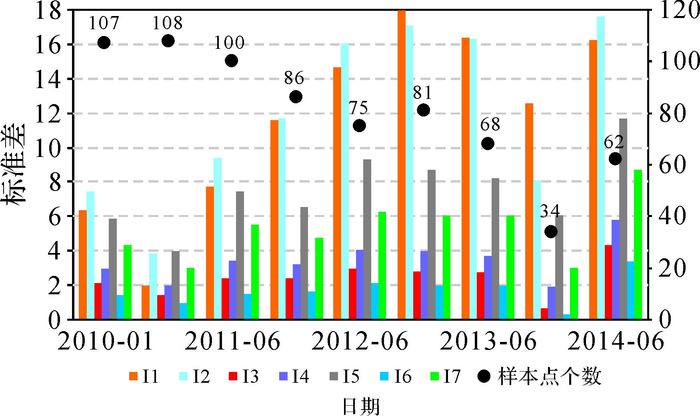
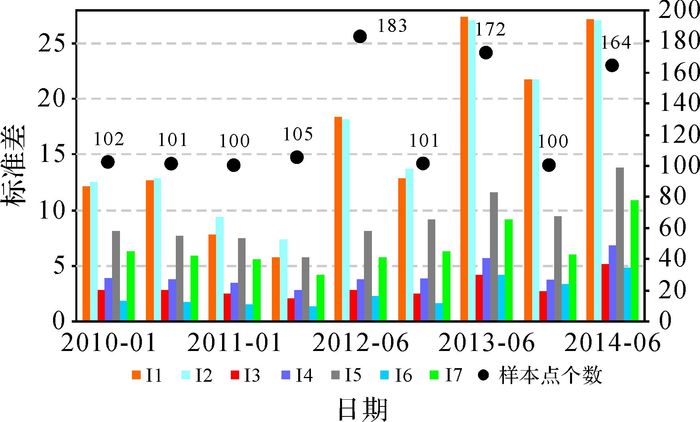
从统计结果可以看出,在样本点相同的情况下,同样的插值分辨率,使用改进的Shepard法插值结果与真值之差的均值、标准差最小,与真值较吻合度较高。为了进一步验证这一结果,图 2、图 3给出了所有插值结果与真值差值的标准差,可以看出同一期数据,改进的Shepard法标准差最小;此外,在插值范围内,样本点为100个左右时,插值结果与真值差值标准差整体较小,虽然第1组2014年1月的数据样本点仅有34个,但十分均匀地分布于插值范围内,因此其标准差也相对较小,可以得出:在插值方法、插值范围、插值分辨率确定的情况下,获得较好插值结果的主要元素是一定数量分布均匀的样本点。
|
| 图 2 第1组数据反插结果与真值差值标准差 |
|
| 图 3 第2组数据反插结果与真值差值标准差 |
为了进一步验证改进的Shepard法对流动重力插值是否能取得相对较好的结果,对三峡地区106.5°—114°E,30°—34°N区域的3期流动重力数据插值,并反插样本点,获得结果与真值的差值,对其进行统计(见表 3)。可以看出使用改进的Shepard法在小区域内插值效果是较为良好的。
| 参数 | 第1期 | 第2期 | 第3期 |
| 样本点个数 | 32 | 22 | 27 |
| 均值 | 0.017 0 | -0.001 7 | 0.020 0 |
| 标准差 | 0.085 4 | 0.066 6 | 0.143 8 |
| 最小值 | -0.044 0 | -0.248 7 | -0.218 4 |
| 最大值 | 0.389 1 | 0.102 4 | 0.598 7 |
流动重力插值的本质就是一个不确定的估计,是一种通过样本点进行空间建模生成充分逼近样本值空间分布特征的函数方程来模拟未知值的方式。本文通过大量的试验,以验证获得对于流动重力插值结果较好的插值方法,得到以下几点结论:
(1) 在插值分辨率、插值范围、样本点一定的情况下,与球面Kriging、反距离加权法相比较,改进的Shepard法对流动重力的插值能取得较好的结果。
(2) 当插值区域内流动重力样本点的变化较小、不存在异常点时,使用球面Kriging插值会获得连续性好、平滑度较高的插值结果。
(3) 流动重力插值过程中,插值分辨率会影响插值的结果,插值过程中要根据样本点分布特征、插值范围选取适当的分辨率。
(4) 对于地球要素插值,要充分考虑其空间相关性、变异性以及地球物理构造性质,在此基础上选择对应的插值方法会获得较为理想的结果。
随着插值技术的逐步完善成熟,将与插值要素相关的属性数据融入模型进行协同插值已经可行,如降水插值过程中加入高程进行协同插值。对于流动重力,将大地高、潮汐改正等要素融入插值模型将是插值研究的一个新方向。
| [1] | 项爱民, 孙少安, 李辉. 流动重力运行状态及质量评价[J]. 大地测量与地球动力学, 2007, 27(6): 109–114. |
| [2] | 董运洪, 李辉, 薄万举. 流动重力资料处理方法的研究[J]. 山西地震, 2006(2): 34–39. |
| [3] | 陆汉鹏, 郝洪涛, 吕子强. 山东地区流动重力历史资料清理综述[J]. 国际地震动态, 2012(10): 15–22. DOI:10.3969/j.issn.0253-4975.2012.10.005 |
| [4] | 徐遵义, 姜玉祥, 赵亮, 等. 改进的Shepard算法及其在重力异常插值中的应用[J]. 武汉大学学报(信息科学版), 2010, 35(4): 477–480. |
| [5] | 吴太旗, 黄谟涛, 欧阳永忠, 等. 高精度海洋重力异常格网插值技术研究[J]. 测绘科学, 2008, 33(5): 70–72. |
| [6] | 彭泽辉, 李辉, 申重阳, 等. 基于最小二乘配置的重力变化插值方法[J]. 大地测量与地球动力学, 2010, 30(3): 43–46. |
| [7] | 李振海, 汪海洪. 重力数据网格化方法比较[J]. 大地测量与地球动力学, 2010, 30(1): 140–144. |
| [8] | 孙文, 吴晓平, 王庆宾, 等. 高精度重力数据格网化方法比较[J]. 大地测量与地球动力学, 2015, 35(2): 342–345. |
| [9] | 党亚民, 章传银, 陈俊勇, 等. 现代大地测量基准[M]. 北京: 测绘出版社, 2015. |
| [10] | 邓敏, 刘启亮, 吴静. 空间分析[M]. 北京: 测绘出版社, 2015. |
| [11] | 邬伦, 刘瑜, 张晶, 等. 地理信息系统:原理、方法和应用[M]. 北京: 科学出版社, 2001. |
| [12] | BARTIER P M, KELLER C P. Multivariate Interpolation to Incorporate Thematic Surface Data Using Inverse Distance Weighting(IDW)[J]. Computers & Geosciences, 1996, 22(7): 795–799. |
| [13] | RENKA R J. Multivariate Interpolation of Large Sets of Scattered Data[J]. ACM Transactions on Mathematical Software, 1988, 14(2): 139–148. DOI:10.1145/45054.45055 |
| [14] | FRANKE R. Scattered Data Interpolation:Tests of Some Methods[J]. Mathematics of Computation, 1982, 38(157): 181–200. |
| [15] | 孔云峰, 仝文伟. 降雨量地面观测数据空间探索与插值方法探讨[J]. 地理研究, 2008, 27(5): 1097–1108. |
| [16] | 刘登伟, 封志明, 杨艳昭. 海河流域降水空间插值方法的选取[J]. 地球信息科学学报, 2006, 8(4): 75–79. |
| [17] | 朱会义, 刘述林, 贾绍凤. 自然地理要素空间插值的几个问题[J]. 地理研究, 2004, 23(4): 425–432. |
| [18] | 胡明城. 现代大地测量学的理论及其应用[M]. 北京: 测绘出版社, 2003. |


