2. 江南大学信息学院, 江苏 无锡 214000
2. Department of Information Science, Jiangnan University, Wuxi 214000, China
得益于通过智能手机提供基于位置的服务,以及按需服务所具备的市场价值,室内定位技术[1]已经成为未来智能服务的重要研究课题。其应用十分广泛,如商场中的商品定位[2]、停车场的车辆导航[3]等。尽管GPS是目前最流行的定位系统,但GPS并不适用于室内导航[4],因为室内环境和高层建筑会遮蔽信号。与GPS不同,智能手机配备了很多传感器(如加速计、陀螺仪、磁传感器和相机),为开发室内导航技术提供了可能性。
一般而言,使用相机估计用户的位置具备可行性,这是因为相机提供了三维世界和二维图像之间的映射[5]。在已知世界坐标系和相机坐标系之间的相对旋转与平移情况下,可以对用户位置进行计算。该技术也被称为相机外参标定,即通过构建一个投影矩阵以完成相机标定[6]。但是,为估计出一个投影矩阵,必须要得到至少6个空间点坐标及其对应的图像点。而执行最小二乘法或奇异值分解法,从投影矩阵中提取旋转矩阵,会使得计算复杂度变得非常高。此外,还必须获悉相机之间的相关旋转和平移。
用户位置定位问题的求解一般在图像传感器通信[7](imaging sensor communication, ISC)中,通过对LED光强度进行调制,以传送数据并保持恒定的照明度,再使用一个相机对数据进行接收和解码,关于ISC的更多信息可以参阅文献[7]。
为避免ISC求解复杂的数学模型,一般可以利用神经网络。由于神经网络能够求解困难和多样化的问题,因此被用于确定二维图像和三维世界的坐标关系。如文献[8]使用了一个3层前馈神经网络,从两个相机拍摄的影像坐标内提取世界坐标。然而,仅使用一个相机也可能完成这一目的。文献[9]提出的方法采用了一个多层感知器神经网络,将图像坐标转化为世界坐标。文献[10]提出了基准标记的室内定位技术,在提取一个标记特征后,对神经网络进行训练,以估计用户位置。然而,标记方法需要明确的特征标识,对标记的坐标信息要求较高。
与上述方法不同,本文依靠ISC接收LED的坐标信息,然后构建一条穿过LED虚拟投影不变的直线。使用一个简单的几何方程和一个神经网络估计相机指向。而且考虑了一个较广范围的旋转矢量。
1 系统结构本文假设每个LED都安装在一个平面(天花板)上,且均平行于世界坐标系的XOY平面(笛卡尔坐标系),一个LED和一个手机之间通信的发起需要LED和手机相机之间的视距,具体如图 1所示,图中Pitch为俯仰角,Roll为翻滚角,Yaw为偏航角。一般可以考虑相机的xoy平面平行于世界坐标系的XOY平面。在这种情况下,相机坐标系和世界坐标系之间的旋转则变成了z轴(偏航)的一个旋转矢量以及x轴(俯仰)和y轴(翻滚)的一个可忽略的旋转矢量。如图 1(a)所示,相机的xoy平面平行于世界坐标系的XOY平面。由于LED能够通过自身的光线链路传送其坐标信息,可以计算出在世界坐标系统中连接任意两个LED的直线的斜率。由此可以建立一个关系,以计算相机坐标的x轴与世界坐标系X轴之间的角度,该角度即是z轴(偏航)的一个旋转矢量。

|
| 图 1 世界坐标系统和相机坐标系的示意图 |
这里X轴和Y轴的旋转矢量是可忽略的。偏航角度的计算如图 2所示。如果(XW1, YW1, Z)和(XW2, YW2, Z)为两个LED的坐标信息,则有
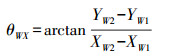 (1)
(1)
|
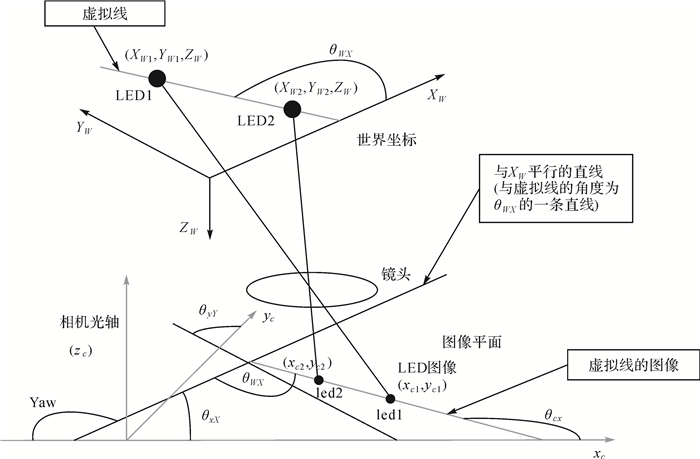
| 图 2 偏航(Yaw,Z轴旋转矢量)角度的计算 |
式中,θWX为一个平面中连接两个LED直线的倾斜角,该平面平行于世界坐标系的XOY平面。
如图 2所示,(xc1, yc1)和(xc2, yc2)分别为一个相机的图像平面上代表LED图像的两个点,则通过相机的z轴旋转矢量进行考虑,利用在世界坐标系中连接两个LED的直线斜率(θWX),以及在相机坐标系中连接两个LED图像的直线斜率,可以计算出相机坐标系和世界坐标系之间的相关旋转。因此有
 (2)
(2) 式中,θcx和k满足如下关系
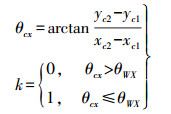 (3)
(3) 式中,θxX是相机坐标系的x轴和世界坐标系的X轴之间的角度,也是y轴和Y轴之间的角度,因为X轴和Y轴在任何一个坐标系中均为正交。根据图 2,θxX是一个相机坐标系到世界坐标系的Z轴的旋转矢量。因此,世界坐标系到相机坐标系统的偏航角(κ)为
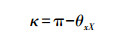 (4)
(4) 以上解释仅当偏航小于π时是正确的。在偏航大于π时也可以对偏航角度进行度量。算法1给出了如何度量偏航大于π的偏航角。该算法是基于镜头的特有性质,即如图 2所示,镜头总是在成像平面上将图像反转。此处LED1和LED2在一个成像平面中互相交换位置。由此可以得出xc1>xc2以及XW1 < XW2。如果θWX=0,则对于所有θxX < π/2,该条件为真。在θxX=π/2时,LED1和LED2图像点之间的斜率将为无穷大,即xc1=xc2。在该条件下,俯仰和翻滚均为零。
因此,总结如下:对于角度较小的俯仰和翻滚,算法1是可行的。在俯仰和翻滚的角度较大的情况下,LED将会失焦,将无法度量相机位置。
2 基于神经网络的定位方法神经网络可以对输入和输出间的任何关系(线性或非线性)进行学习。在本文的模型中使用了多层感知器(multiple-layer perceptron, MLP),MLP能够通过监督式训练及误差反向传播算法,求解困难和多样化的问题。
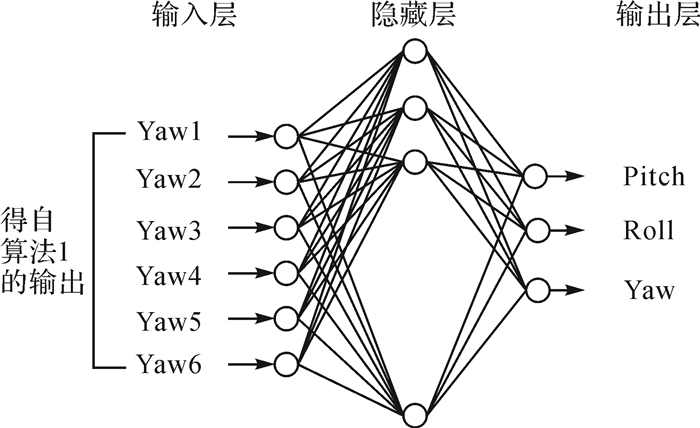
2.1 利用神经网络估计旋转矢量训练神经网络[11-12]使用上一节描述的方法,从计算出的平行线偏航中对旋转矢量(俯仰、翻滚和偏航)进行估计。本文的神经网络结构如图 3所示,其中使用了4个LED,以构建6条虚拟直线,从这些直线中计算出6个偏航角度。本文使用一个3层前馈网络,其中隐藏层由25个神经元组成。隐藏层中的所有神经元都有一个tan-sigmoid传递函数以适应非线性。对于输出层神经元,使用了线性传递函数。
|
| 图 3 本文的神经网络结构 |
该神经网络的训练方法如算法2所示。首先,通过模拟不同位置和旋转矢量的相机模型,创建一个训练数据库。每次从4个LED图像中计算出6个偏航角度,并存储在训练数据库中。将俯仰和翻滚的角度范围分别设置为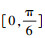

算法2步骤:
(1) 以不同相机位置和旋转仿真储相机模型;
(2) 得到LED图像坐标;
(3) 使用算法1得到6个偏航,建立神经网络输入数据库;
(4) 输入数据库进行数据训练和测试工作;
(5) 确定某个旋转矢量(俯仰、翻转和偏航);
(6) 使用相机模型为该旋转矢量和房间内所有位置进行模拟,得到每个相机位置LED图像坐标;
(7) 使用算法1计算出6个偏航角,将其反馈为神经网络的输入;
(8) 由步骤(4)和步骤(7)共同得出神经网络输出。
2.2 世界坐标系中的相机位置估计共线条件被用于建立二维图像与三维空间点之间的关系。根据这一条件,每个目标点及其图像和投影中心,都应属于同一直线。可表示如下[13]
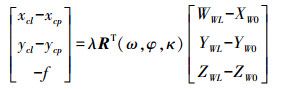 (5)
(5) 式中,(xcl, ycl)表示相机坐标系中的目标图像点(LED图像);(xcp, ycp)表示相机坐标系统中的投影中心坐标;(XWL, YWL, ZWL)表示世界坐标系统中的目标点坐标;(XW0, YW0, ZW0)表示世界坐标系统中的相机位置;RT(ω, φ, κ)表示世界坐标系和相机坐标系之间的相对旋转;f表示相机镜头的焦距;λ表示比例因子。
旋转矩阵R是旋转矢量俯仰、翻滚和偏航的函数,因此可以使用神经网络的输出构建该矩阵。此外,LED坐标XWL可以通过链路接收到,LED图像坐标xcl可以通过对图像的特征进行提取获取,因此如果获得相机投影中心和焦距,则可以通过求解式(7)估计出未知的相机位置(用户位置)。相机进行标定的方法比较成熟,也比较多,如七参数模型[14]。按照文献[15]的方法,为了从式(5)中消除λ,可以作如下调整
 (6)
(6) 式中,(xcl, ycl)表示相机坐标系中的LED图像点,对于LED1和LED2,l=1或者2;(xcp, ycp)表示相机坐标系中投影中心的坐标;(XWL, YWL, ZWL)表示世界坐标系统中的LED位置,对于LED1和LED2,L=1或者2;(XW0, YW0, ZW0)表示世界坐标系中的相机位置;rij表示旋转矩阵RT(ω, φ, k);f为相机镜头的焦距。
3 仿真试验结果与分析仿真试验参数见表 1。天花板上放置了4个LED;从距离地面1500 mm的高度对相机性能进行评估。考虑了4种情形,相机的旋转矢量分别为
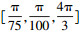
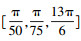
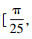
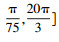
| 参数 | 数值 |
| 房间面积/mm3 | 5000×5000×3500 |
| LED位置(LED1,LED2,LED3,LED4) | (2000,2000,3500) |
| (3000,2000,3500) | |
| (3000,3000,3500) | |
| (2000,3000,3500) | |
| 接收平面高度(Z)/mm | 1500 |
| 焦距f/mm | 1.3 |
| 图像尺寸/像素 | 1920×3096 |
| 投影中心 | (910,1548) |
| 偏斜 | 0 |
4个LED的位置保持固定不变,对X轴旋转(俯仰)向量进行估计的误差见表 2,对Y轴旋转(翻滚)向量进行估计的误差见表 3,对Z轴旋转(偏航)向量进行估计的误差见表 4。为避免LED和相机之间的非视距情况,x轴和y轴旋转矢量必须保持低量值。因此,所有情形的俯仰和翻滚均被保持在较低量值。从表 2—表 4的情形1结果可以看出,估计出的俯仰误差低于0.001。但是,在表 2中,随着x轴旋转矢量的增长,性能出现了下降。表 3给出了神经网络对于y轴旋转矢量(翻滚)的性能。神经网络在对y轴的旋转矢量进行估计时性能没有达到处理x轴旋转矢量时的精确度;但是,该神经网络在面对所有旋转矢量时表现出了稳定的性能。表 4给出了神经网络在估计偏航时的性能。同样的,由表 4中第3行可以看出,随着俯仰和翻滚的增加,神经网络的性能出现了下降。表 4中情形3和情形4给出了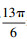
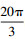
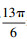
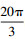
| 情形 | LED1 | LED2 | LED3 | LED4 |
| 1 | 0.005 0 | 0.005 2 | 0.003 9 | 0.003 8 |
| 2 | 0.004 8 | 0.004 9 | 0.003 0 | 0.004 1 |
| 3 | 0.007 0 | 0.005 1 | 0.003 9 | 0.003 6 |
| 4 | 0.006 0 | 0.006 0 | 0.900 0 | 0.270 0 |
| 情形 | LED1 | LED2 | LED3 | LED4 |
| 1 | -0.017 7 | -0.017 0 | -0.019 1 | -0.017 2 |
| 2 | -0.017 1 | -0.018 0 | -0.017 1 | -0.018 3 |
| 3 | -0.022 5 | -0.020 1 | -0.022 5 | -0.020 4 |
| 4 | -0.022 6 | -0.018 6 | -0.022 6 | -0.018 0 |
| 情形 | LED1 | LED2 | LED3 | LED4 |
| 1 | -0.005 0 | 0.000 0 | -0.005 0 | 0.000 0 |
| 2 | -0.005 2 | 0.003 1 | 0.000 0 | 0.007 0 |
| 3 | -0.001 0 | -0.000 5 | -0.001 0 | -0.000 5 |
| 4 | -0.001 0 | -0.001 0 | 0.000 8 | 0.001 0 |
首先使用神经网络输出(俯仰、翻滚和偏航),利用式(6)计算相机位置;其次从估计出的相机位置计算出均方根(RMS)误差;神经网络对于各旋转矢量的输出用于计算相机的位置,最后再计算RMS误差。4种情形的误差如图 4所示,图中,LED1、LED2、LED3和LED4的位置分别表示为符号*、●、■和▲。由图 4可以看出,当x轴和y轴旋转矢量较小时,误差较低。图 4(a)和图 4(b)的RMS误差最高为100 mm。然而,对于房间中的大部分地方,RMS误差在35 mm之内。
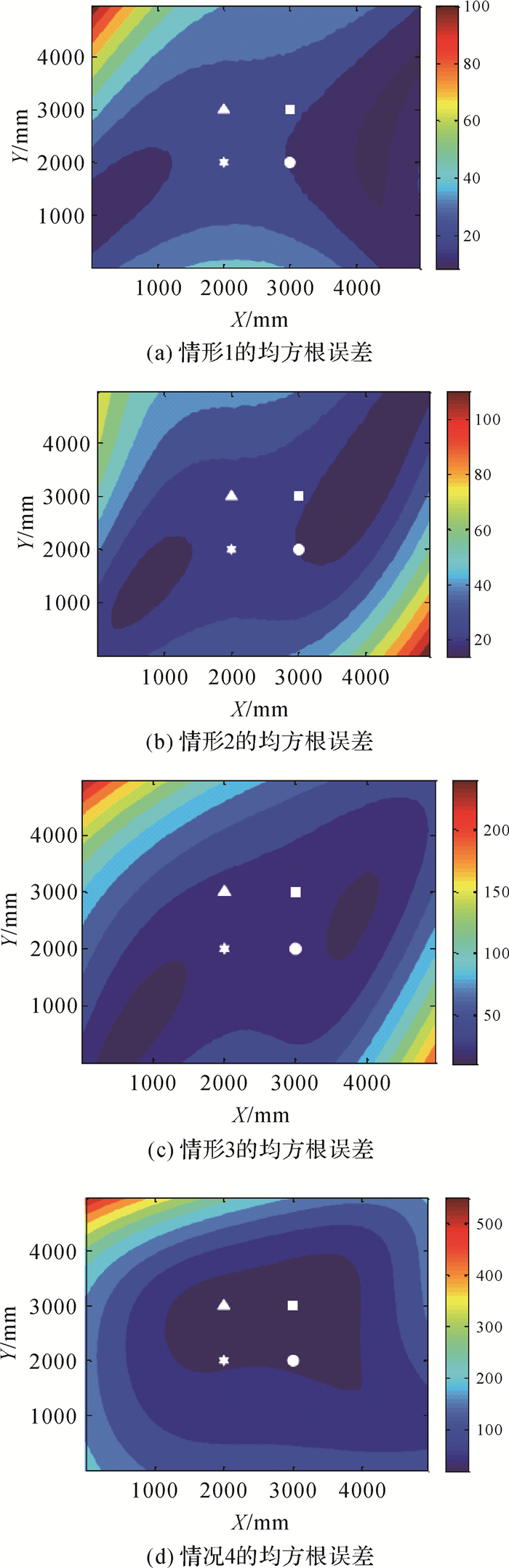
|
| 图 4 本文提出方法的定位性能 |
由于各定位方法的试验环境有所差异,试验方法也不尽相同。为了公平起见,本文不作具体详细的数值比较,只作总结性比较和分析。
文献[8-10]仅对偏航进行估计,忽略了俯仰和翻滚。本文提出的方法使用了一个神经网络,对其他两个旋转矢量(俯仰和翻滚)也进行了估计,同时充分利用LED光线的投影不变性,借助ISC完成虚拟直线的构建。其他具体比较信息见表 5,可以看出本文方法综合性能更优。
由于三维场景和拍摄到的二维图像之间存在着非线性和高度复杂的关系,使用一个相机对用户的位置进行估计需要研究复杂的数学模型。而神经网络可最大限度地减少该复杂关系。为此,本文提出了一种基于神经网络的定位方法,而且考虑了较广范围的旋转矢量。仿真结果表明,该方法在x轴和y轴旋转矢量较低时性能较优,但是当x轴和y轴旋转矢量较大时误差会增加。未来将会研究如何降低x轴和y轴旋转矢量带来的误差。
| [1] | 苏松, 胡引翠, 卢光耀, 等. 低功耗蓝牙手机终端室内定位方法[J]. 测绘通报, 2015(12): 81–84. |
| [2] | 鲍向华. 基于室内定位技术的商场导购系统的设计与开发[D]. 长春: 吉林大学, 2015. |
| [3] | 周亮, 付永涛, 李广军. 无线定位与惯性导航结合的室内定位系统设计[J]. 电子技术应用, 2014, 40(4): 73–76. |
| [4] | 孔天恒. 基于Radar-scanner/INS的微小型旋翼无人机室内组合导航与控制的研究[D]. 杭州: 浙江大学, 2014. |
| [5] | 郭涛, 达飞鹏, 方旭. 小视场环境下的摄像机标定[J]. 中国激光, 2012, 39(8): 164–168. |
| [6] | LIU G H, WANG W B, YUAN J Y, et al. A Novel Camera Calibration Method of Variable Focal Length Based on Single-view[C]//International Symposium on Electronic Commerce and Security.Nanchang:IEEE, 2009:125-128. |
| [7] | SAHA N, IFTHEKHAR M S, LE N T, et al. Survey on Optical Camera Communications:Challenges and Opportunities[J]. Iet Optoelectronics, 2015, 9(5): 172–183. DOI:10.1049/iet-opt.2014.0151 |
| [8] | IFTHEKHAR M S, MONDAL R K, LE N T, et al.Simple Method for Indoor Localization in OCC Using Smart Phone Image Sensor[C]//Ubiquitous and Future Networks.Shanghai:IEEE, 2014:55-58. |
| [9] | 柯炜, 吴乐南, 殷奎喜. 基于神经网络的数字广播信号无线定位算法[J]. 东南大学学报(英文版), 2010, 26(3): 394–398. |
| [10] | MAZAN F, KOVAROVA A.Optimizing Artificial Neural Network for Beacon Based Indoor Localization[C]//International Conference on Computer Systems and Technologies.New York:ACM, 2016:261-268. |
| [11] | SIMONHAYKIN. 神经网络与机器学习(英文版)[M]. 3版.北京: 机械工业出版社, 2009. |
| [12] | 许雄, 钟燕飞, 张良培, 等. 基于空间自相关BP神经网络的遥感影像亚像元定位[J]. 测绘学报, 2011, 40(3): 307–311. |
| [13] | 付强, 王春平. 一种点目标三维重构的新算法[J]. 科学技术与工程, 2008, 8(3): 643–647. |
| [14] | 李东, 毛之琳, 廖文兵, 等. CGCS2000向独立坐标系转换的精度分析与估计研究[J]. 测绘通报, 2013(10): 8–10. |
| [15] | QI Z, XIAO L, FU S, et al. Two-step Camera Calibration Method Based on the SPGD Algorithm[J]. Applied optics, 2012, 51(26): 6421–6428. DOI:10.1364/AO.51.006421 |



