2. 中铁第一勘察设计院集团有限公司, 陕西 西安 710043;
3. 甘肃铁道综合工程勘察院有限公司, 甘肃 兰州 730000
2. China Railway First Survey and Design Institute Group Co. Ltd., Xi'an 710043, China;
3. The General Engineering Survey Institute of Railways of Gansu Co. Ltd., Lanzhou 730000, China
高斯-克吕格投影(以下简称高斯投影)是一种等角投影,应用比较广泛,被许多国家用作地形图的数学基础[1-3]。高斯投影的特点是中央经线和赤道投影是垂直的直线,中央经线投影后保持长度不变,投影无角度变形。由于高斯投影是在地球椭球面上采用等角横切椭圆柱进行投影,因此无法利用球面坐标计算,其公式计算十分复杂和烦琐[4-5]。为此,在保留高斯投影的前两个条件下,本文研究了一种等距离球面高斯投影,即一种双重高斯投影:首先从椭球面投影到等距离球面上,再从等距离球面上采用横轴圆柱投影到平面上。等距离球面高斯投影可直接利用球面坐标计算,简化了各种与投影相关的计算。本文着重分析等距离球面高斯投影的各种数学性质和变形情况,并与高斯投影进行比较,进而说明等距离高斯投影的可用性。
1 等距离球面高斯投影 1.1 等距离球面高斯投影公式若先将地球椭球面按一定法则投影到一个球面上,经度坐标l不变,球面纬度坐标φ是大地纬度B的函数;再将球面按照等角横切圆柱投影到平面上(球面高斯投影)。这样的双重投影显然满足中央经线和赤道投影是垂直的直线,若还要中央经线投影后保持长度不变,由于球面按照等角横切圆柱投影到平面上时中央经线投影后保持长度不变,因此地球椭球面投影到球面上时也必须要保持中央经线投影后长度不变,那么这个球面就必然是等距离纬度球面,即球面纬度坐标φ就是等距离纬度ψ。
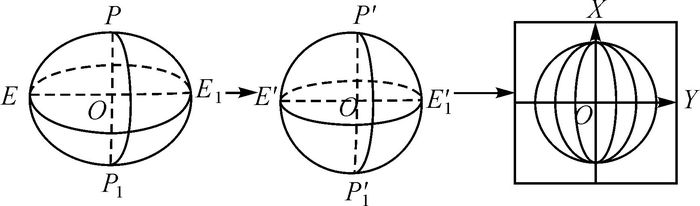
等距离球面高斯投影是一种双重投影,先投影到球面上,再投影到平面上,如图 1所示。由球面高斯投影(球面横墨卡托投影)的闭合公式,从等距离球面上投影到平面时,对球面上的一点(ψ, l),对应的投影平面坐标(x, y)为[6-7]
|
| 图 1 等距离球面高斯投影示意图 |
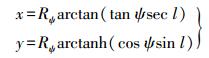 (1)
(1) 式中,(ψ, l)为点在等距离球面上的经纬度;(x, y)为投影平面坐标;Rψ为等距离球半径
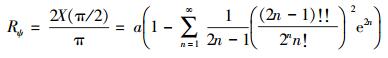 (2)
(2) 从地球椭球面上投影到等距离球面上时,经度坐标不变,纬度坐标ψ是大地纬度B与椭球第一偏心率e的函数,等于子午线弧长除以等距离球半径,即ψ=X/Rψ,具体展开式为
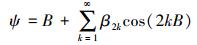 (3)
(3) 式中,等距离纬度关于大地纬度的正解展开式系数βk也可参考文献[8-9]。
结合式(1)及等距离纬度关于大地纬度的展开式,即等距离球面高斯投影公式,联系等距离纬度反解公式,可得球面高斯投影的反解公式为
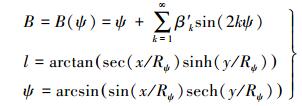 (4)
(4) 式中,等距离纬度关于大地纬度的反解展开式系数βk′可参考文献[8-9]。
1.2 等距离球面高斯投影经纬网投影平面上所建立的经纬网构成了地图投影的数学基础。根据投影公式(1),经过推导,消去经纬度坐标,可得等距离球面高斯投影子午线和纬线圈的投影方程
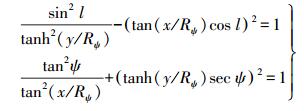 (5)
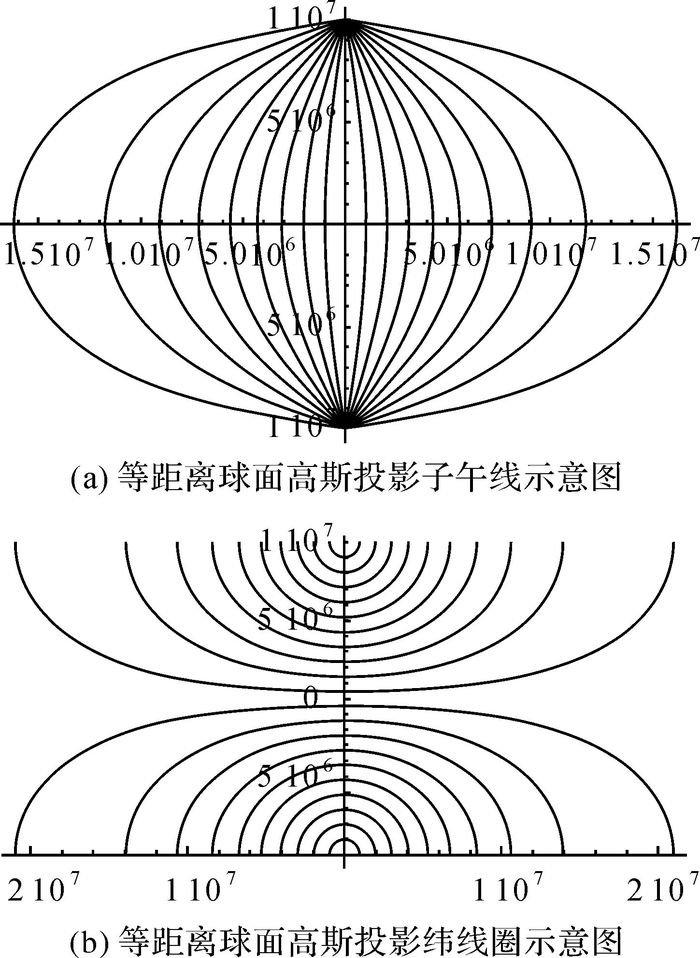
(5) 取CGCS2000参考椭球[10-11],根据式(1),可以绘出等距离球面高斯投影的子午线和纬线圈投影示意图,如图 2所示。
|
| 图 2 |
从图 2可以看出,等距离球面高斯投影的子午线投影为汇聚到极点的曲线,在极点附近接近于直线;等距离球面高斯投影的纬线圈投影接近于椭圆的曲线,将南北半球的纬线圈投影拼合在一起可以得到类似于椭圆的闭合曲线;等距离球面高斯投影的经纬线投影仍然正交。
2 等距离球面高斯投影变形分析 2.1 长度变形尽管等距离球面高斯投影在从球面投影到平面时是等角投影,但从椭球面投影到球面时是等距离投影,而非等角投影,因此椭球面上的各个方向长度比不相等。由于等距离球面高斯投影的经纬线投影仍然正交,故经纬线长度比m、n与极值长度比a、b一致。为分析等距离球面高斯投影的长度变形,先求得一阶偏导数
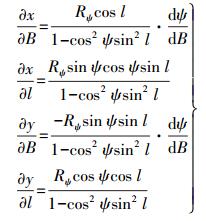 (6)
(6) 式中,等距离纬度对大地纬度的导数闭合形式为(M为子午圈曲率半径)
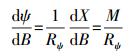 (7)
(7) 或有级数形式
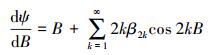 (8)
(8) 由式(6)可得
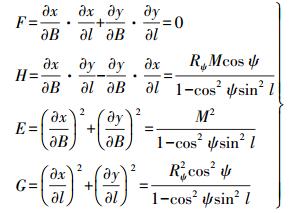 (9)
(9) 因此,经纬线交角投影后的角度与90°的差值ε为
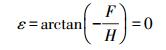 (10)
(10) 表明等距离球面高斯投影的经纬线投影仍然正交。
经纬线长度比m、n为
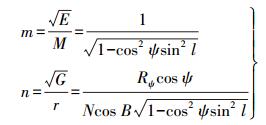 (11)
(11) 式中,r=Ncos B,N为卯酉圈曲率半径。
根据式(11),可以绘出一个6°条带内等距离球面高斯投影的经纬线长度比(极值长度比)示意图,如图 3所示。由于等距离高斯投影在南北半球内的投影对称,故只分析北半球的情况。
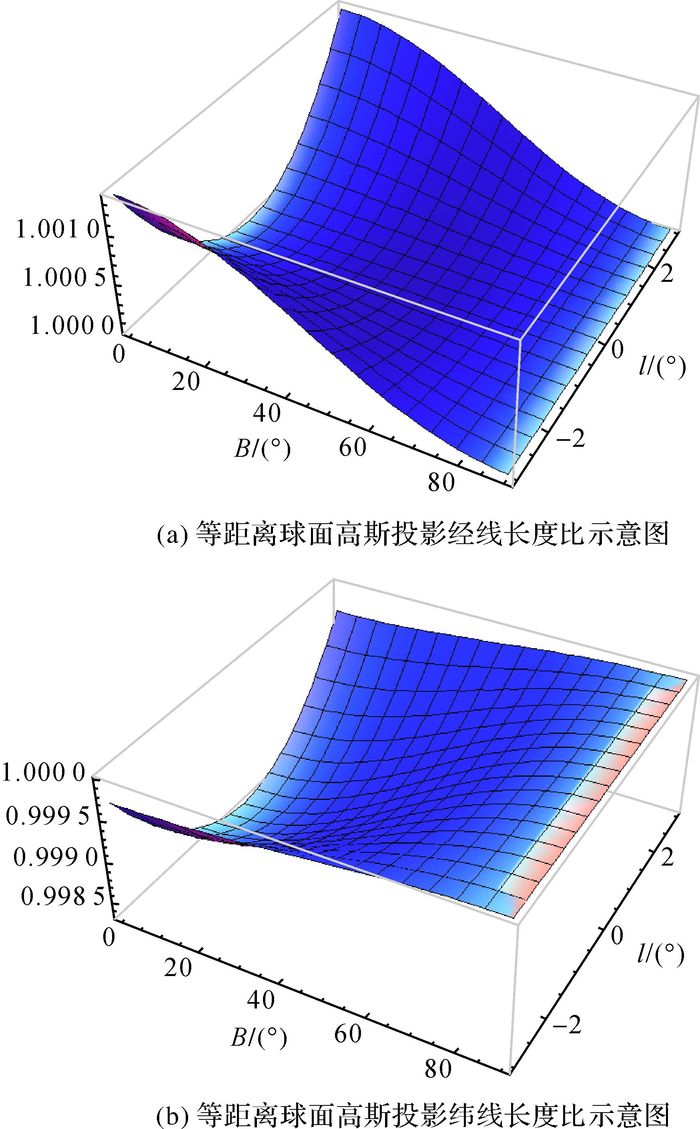
|
| 图 3 |
从图 3可以看出,在[-3°, 3°]带内,等距离球面高斯投影经线长度比m随纬度增大逐渐减小,随经度增大逐渐增大,等距离球面高斯投影经线长度比n随纬度增大逐渐增大,随经度增大逐渐增大;长度变形m-1、n-1绝对值均随纬度增大而减小,m-1绝对最大值在边界处,为0.001372,n-1绝对最大值在原点处,为0.001676,绝对值均在0.001676范围内,因此长度变形vμ=±max(|m-1|, |n-1|)绝对最大值不超过0.1676%;m始终大于等于1,n始终小于等于1,说明m是极大长度比,n是极小长度比。长度变形m-1为正数,随点远离极点而增大,长度变形n-1为负数,绝对值随点远离原点而减小。另外,在更大的椭球面范围内,m-1为正数,n-1有正有负,但m始终大于n。
2.2 角度、面积变形等距离球面高斯投影并不是一个等角投影,存在一定的角度变形,最大角度变形ω为
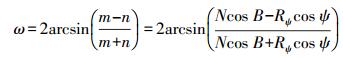 (12)
(12) 由式(12)可知,ω仅与纬度坐标有关,与经度坐标无关。根据式(12),可以绘出一个6°条带内等距离球面高斯投影的角度变形示意图,如图 4所示。
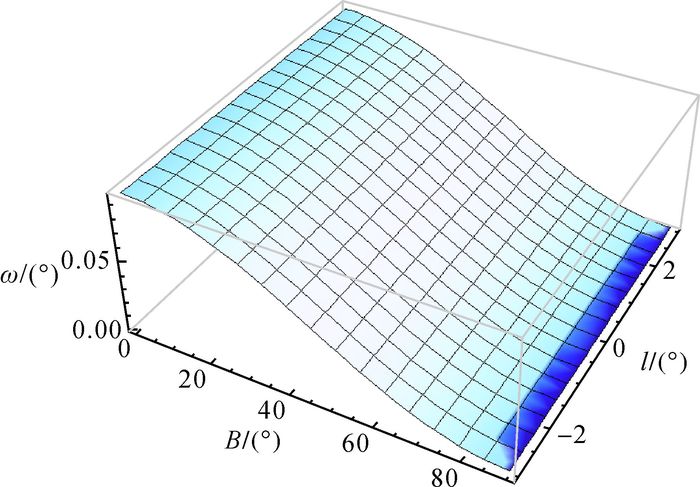
|
| 图 4 等距离球面高斯投影角度变形示意图 |
从图 4可以看出,等距离球面高斯投影的角度变形都随纬度增大而减小,与经度无关,最值在纬线圈B=0即赤道处,约为0.09609°=5.765′。
等距离球面高斯投影有面积变形,面积比P为
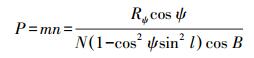 (13)
(13) 面积变形
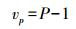 (14)
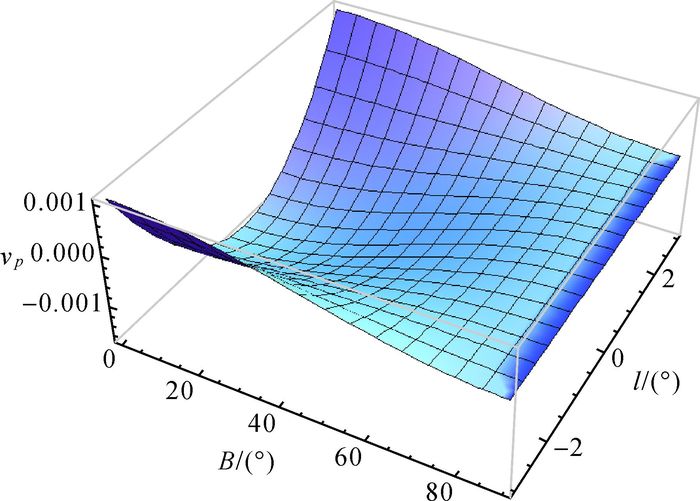
(14) 根据式(14),可以绘出一个6°条带内等距离球面高斯投影的面积变形示意图,如图 5所示。
|
| 图 5 等距离球面高斯投影面积变形示意图 |
从图 5可以看出,在[-3°, 3°]带内,面积变形较小,绝对值最大值在原点处,约为0.001676。
2.3 子午线收敛角任意一点处的子午线收敛角是过该点所引经线与X轴正向的夹角,根据文献[1],结合式(6),可推得投影平面第一象限内的子午线收敛角为
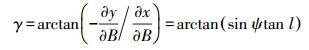 (15)
(15) 结合投影反解式(4),式(15)还可以表示为投影平面坐标(x,y)的函数
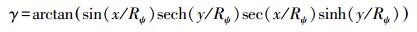 (16)
(16) 经纬线长度比m、n,以及角度/面积变形也可以表示成(x,y)的函数。
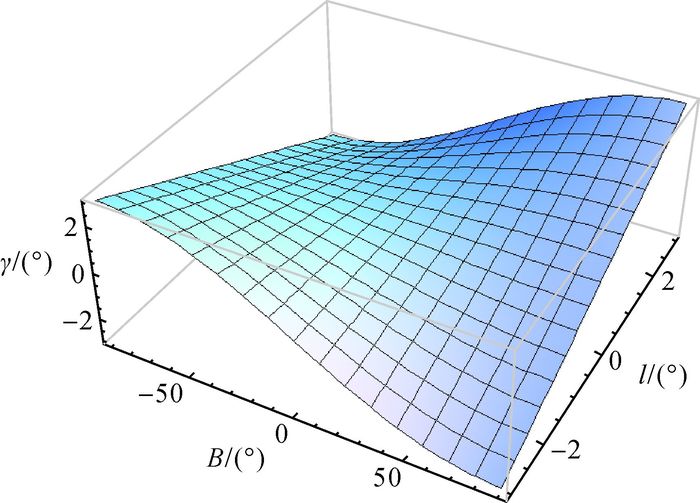
根据式(15),可以绘出一个6°条带内等距离球面高斯投影的子午线收敛角示意图,如图 6所示;由于子午线收敛角在南北半球也有区别(互为正负关系),故绘出一个6°条带全部区域内的子午线收敛角示意图。
|
| 图 6 等距离球面高斯投影子午线收敛角示意图 |
从图 6可以看出,在6°条带内,子午线收敛角绝对值随经纬度绝对值增大而增大,在原点处为0,随点远离极点逐渐增大,在边界处(B, l)=(±90°, ±3°)处取得最大值, 为±3°。
3 与传统高斯投影比较分析可以看出,等距离球面高斯投影保持了投影前后中央子午线无变形和投影后中央经线仍与赤道垂直的性质,但并不是严格意义上的等角投影,与传统高斯投影还是有区别的。为此,下面研究二者之差异。
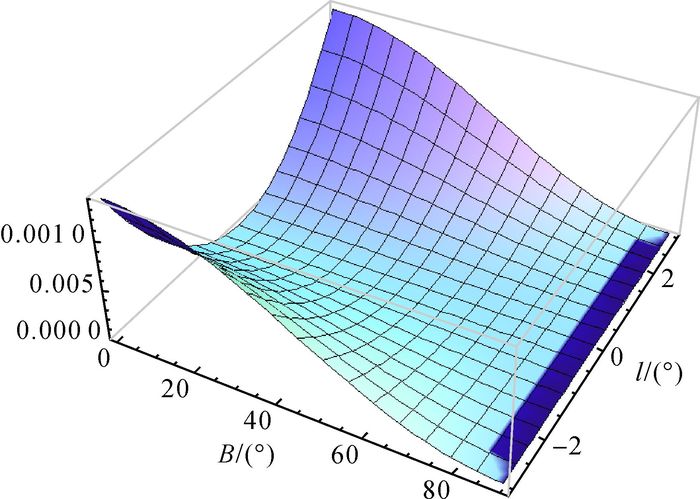
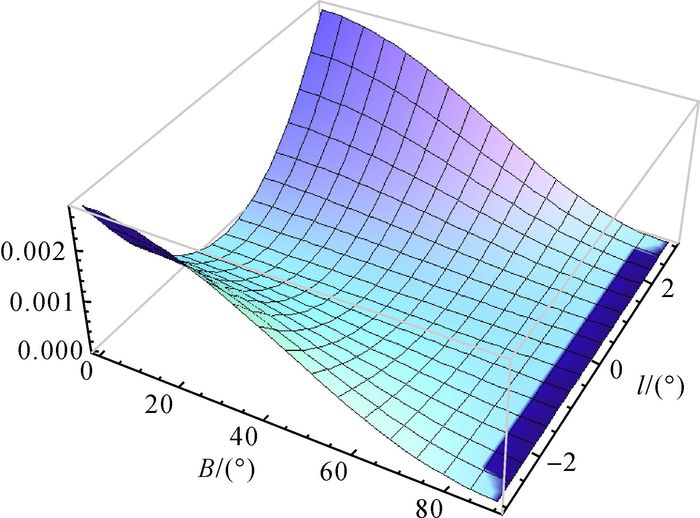
设高斯投影平面坐标为(x′, y′),投影长度变形、角度变形、面积变形及子午线收敛角分别为vμ′、ω′、vp′、γ′(ω′=0)。根据相应的投影和变形计算公式[1, 7, 12-13],可以绘出高斯投影变形参数vμ′、vp′在一个6°条带内的示意图,如图 7、图 8所示。由于对称性,故只研究[0, 3°]条带内等距离球面高斯投影与传统高斯投影的变形差异,设经线长度变形差异Δvμ=(m-1)-vμ′,子午线收敛角差异Δγ=γ-γ′,平面坐标差异Δx=x-x′、Δy=y-y′,分别列于表 1、表 2、表 3、表 4;值得注意的是,m≥1,高斯投影是等角投影,故Δω=ω-ω′=ω,已在图 4中体现,椭球参数取CGCS2000参数。
|
| 图 7 高斯投影vμ′示意图 |
|
| 图 8 高斯投影vp′示意图 |
| l/(°) | B/(°) | ||||||
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | |
| 0 | 1.110×10-15 | -4.441×10-16 | 1.776×10-15 | 7.772×10-15 | 1.465×10-14 | -7.550×10-15 | 0 |
| 0.5 | -2.566×10-7 | -1.995×10-7 | -7.258×10-8 | 3.176×10-8 | 5.606×10-8 | 2.292×10-8 | 0 |
| 1 | -1.027×10-6 | -7.982×10-7 | -2.903×10-7 | 1.271×10-7 | 2.243×10-7 | 9.168×10-8 | 0 |
| 1.5 | -2.311×10-6 | -1.797×10-6 | -6.532×10-7 | 2.863×10-7 | 5.047×10-7 | 2.063×10-7 | 0 |
| 2 | -4.112×10-6 | -3.196×10-6 | -1.161×10-6 | 5.096×10-7 | 8.975×10-7 | 3.667×10-7 | 0 |
| 2.5 | -6.430×10-6 | -4.997×10-6 | -1.814×10-6 | 7.976×10-7 | 1.403×10-6 | 5.729×10-7 | 0 |
| 3 | -9.268×10-6 | -7.201×10-6 | -2.612×10-6 | 1.151×10-6 | 2.021×10-6 | 8.249×10-7 | 0 |
| (″) | |||||||
| l/(°) | B/(°) | ||||||
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | -2.186 | -3.399 | -3.210 | -1.969 | -0.5892 | 0 |
| 1 | 0 | -4.374 | -6.800 | -6.421 | -3.938 | -1.178 | 0 |
| 1.5 | 0 | -6.565 | -10.20 | -9.633 | -5.907 | -1.767 | 0 |
| 2 | 0 | -8.761 | -13.61 | -12.85 | -7.875 | -2.355 | 0 |
| 2.5 | 0 | -10.96 | -17.03 | -16.07 | -9.843 | -2.943 | 0 |
| 3 | 0 | -13.17 | -20.45 | -19.29 | -11.81 | -3.530 | 0 |
| m | |||||||
| l/(°) | B/(°) | ||||||
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | |
| 0 | 0 | -3.541×10-10 | 2.124×10-9 | 8.497×10-9 | 2.974×10-8 | 3.965×10-8 | 0 |
| 0.5 | 0 | -0.3795 | -0.5295 | -0.4088 | -0.1775 | -0.02751 | 0 |
| 1 | 0 | -1.519 | -2.118 | -1.635 | -0.7099 | -0.1100 | 0 |
| 1.5 | 0 | -3.418 | -4.768 | -3.679 | -1.597 | -0.2475 | 0 |
| 2 | 0 | -6.080 | -8.479 | -6.541 | -2.839 | -0.4399 | 0 |
| 2.5 | 0 | -9.507 | -13.25 | -10.22 | -4.435 | -0.6870 | 0 |
| 3 | 0 | -13.70 | -19.10 | -14.72 | -6.384 | -0.9887 | 0 |
| m | |||||||
| l/(°) | B/(°) | ||||||
| 0 | 15 | 30 | 45 | 60 | 75 | 90 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | -93.28 | -84.12 | -60.73 | -33.14 | -11.75 | -1.632 | 0 |
| 1 | -186.6 | -168.3 | -121.5 | -66.27 | -23.48 | -3.263 | 0 |
| 1.5 | -280.0 | -252.4 | -182.2 | -99.38 | -35.21 | -4.890 | 0 |
| 2 | -373.5 | -336.7 | -243.0 | -132.5 | -46.91 | -6.514 | 0 |
| 2.5 | -467.1 | -421.1 | -303.7 | -165.5 | -58.58 | -8.131 | 0 |
| 3 | -560.9 | -505.6 | -364.5 | -198.5 | -70.21 | -9.741 | 0 |
由表 1可以看出,在一个6°条带内,等距离球面高斯投影经线长度变形与高斯投影长度变形差异很小,绝对值的最大值取在(B, l)=(0, ±3°)处,为9.268×10-6,二者几乎完全一致;由图 3、图 7、表 1可以看出,由于纬线变形的影响,等距离球面高斯投影长度变形绝对值整体上比高斯投影要大。由图 5、图 8可以看出,等距离球面高斯投影面积变形绝对值比高斯投影要小,前者最大面积变形取在原点处,绝对值为0.001676,后者最大面积变形取在(B, l)=(0°, ±3°)处,为0.002765,后者最大面积变形绝对值是前者的1.65倍。
由表 2可以看出,等距离球面高斯投影子午线收敛角比高斯投影小,但差异很小,最大差值Δγ取在约(B, l)=(±35.3°, ±3°)处,绝对值为20.9954″。
从表 3、表 4可以看出,等距离球面高斯投影平面坐标基本上都比高斯投影更靠近坐标轴,差异Δx随纬度增大先增大后减小,随经度增大而增大,差异Δy随纬度增大而减小,随经度增大而增大,纵坐标最大差值取在约(B, l)=(±30°, ±3°)处,绝对值为19.10m,横坐标最大差值取在约(B, l)=(0, 3°)处,绝对值为560.9m。
4 结语本文研究了等距离球面高斯投影,通过分析等距离球面高斯投影的各种数学性质及变形情况,并与高斯投影进行比较,确定了等距离球面高斯投影的可用性。等距离球面高斯投影经纬网投影保持正交,在一个6°条带内,最大长度变形绝对值为0.1676%,最大角度变形绝对值为5.765′,最大面积变形绝对值为0.1676%,子午线收敛角最大值为3°。等距离球面高斯投影经线长度变形与高斯投影几乎一致,子午线收敛角差异很小,角度变形比高斯投影大,面积变形比高斯投影小。总的来说,等距离球面高斯投影各变形参数与传统高斯投影相当。虽然等距离球面高斯投影不是等角投影,但有能基于球面坐标直接进行换算、面积变形较小等优势,有一定的理论价值和应用前景。
| [1] | 孙达, 蒲英霞. 地图投影[M]. 南京: 南京大学出版社, 2005. |
| [2] | 陈键, 晁定波. 椭球大地测量学[M]. 北京: 测绘出版社, 1989. |
| [3] | GRAFAREND E W, KRUMM F W. Map Projections[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2014. |
| [4] | GRAFAREND E W. The Optimal Universal Transverse Mercator Projection[C]//Geodetic Theory Today. Berlin:Springer Berlin Heidelberg, 1995:51-51. |
| [5] | DEAKIN R E, HUNTER M N, KARNEY C F F. The Gauss-Krüger Projection[C]//Victorian Regional Survey Conference. Warrnambool:[s.n.], 2010. |
| [6] | 李忠美, 于金星, 李厚朴, 等. 高斯投影与横墨卡托投影等价性证明[J]. 海洋测绘, 2013, 33(3): 17–20. |
| [7] | PETER O. The Mercator Projections[M]. Edinburgh: Edinburgh University Press, 2008: 23-29. |
| [8] | 李厚朴, 边少锋, 钟斌. 地理坐标系计算机代数精密分析理论[M]. 北京: 国防工业出版社, 2015. |
| [9] | 杨启和. 地图投影变换原理与方法[M]. 北京: 解放军出版社, 1989. |
| [10] | 魏子卿. 2000中国大地坐标系[J]. 大地测量与地球动力学, 2008, 28(6): 1–5. |
| [11] | 程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS80和WGS84的比较[J]. 测绘学报, 2009, 38(3): 189–194. |
| [12] | DEAKIN R E, HUNTER M N, KARNEY C F F. The Gauss-Krueger Projection:Karney-Krueger Equations[C]//The 25th International Cartographic Conference. Paris:[s.n.], 2011. |
| [13] | KARNEY C F F. Transverse Mercator with an Accuracy of a Few Nanometers[J]. Journal of Geodesy, 2011, 85(8): 475–485. DOI:10.1007/s00190-011-0445-3 |


