对流层延迟改正建模是全球卫星导航系统(global navigation satellite system, GNSS)研究的一个重要方向。对流层延迟模型可表示为
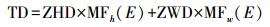 (1)
(1) 式中,TD为对流层延迟,它是指在卫星和接收机之间对流层信号的延迟;ZHD是天顶干延迟;ZWD是天顶湿延迟;MFh(E)是在高度角E下ZHD部分的映射函数;MFw(E)是在高度角E下ZWD部分的映射函数。
ZTD建模是对流层延迟建模的一个重要组成部分,它的任务是确定ZHD和ZWD。目前,根据ZTD模型的使用条件可以分为两大类模型。一种类型为基于实测气象参数的ZTD模型,这一类模型是基于用户位置实测的气象数据来计算ZTD,包括Hopfield模型、Saastamoinen模型和Black模型。这些模型的特征是通过在GNSS天线所在位置实测的气象元素(如大气压力PS、温度TS和水汽压力eS)来表达ZHD和ZWD,其缺陷是并非所有GNSS接收机都具有气象传感器或具有能够获取实测气象参数的条件。另一种类型为经验ZTD模型, 其特点是使用一些经验数据建立对流层延迟模型。其中, UNB3m和EGNOS[1]是两种早期使用的经验ZTD模型。试验表明, UNB3m和EGNOS精度较低且呈现出较大的系统偏差。为此,一些学者提出了一些更高精度的经验ZTD模型,如国外学者提出的GPT2模型[2-3]、GPT2w模型[4]、TropGrid2模型[5]等;国内学者提出的ITG模型[6]、IGGtrop模型[7]和GZTD模型[8]等。这些新提出的模型比UNB3m和EGNOS模型在精度上有很大的提高。同时,其全球范围内的精度大致为3.5~4.0 cm。这些模型的缺陷是需要大量的外部格网数据作为初始使用条件,如GPT2w模型需要约1 632 000个外部格网数据作为输入,这限制了GNSS用户的使用。
另外,神经网络技术具有强大的非线性拟合能力,且单一神经网络模型就可以表达非常复杂的非线性问题[9],在基于实测气象参数型的ZTD建模中已经取得了一定的成果。这些神经网络模型大多以GNSS接收机天线位置的实测气象数据作为神经网络的输入参数。由于经验ZTD模型与基于实测气象参数的ZTD模型的建模机制和使用条件不一样,因此构造经验ZTD的神经网络模型需要依据该类模型建模机制。同时,国内虽然有部分学者[4, 10]构建了神经外网络的经验ZTD模型,但依旧存在以下不足:首先,他们的神经网络模型仅考虑将坐标作为输入,忽略了ZTD时间变化的周期性特征,只适合短期预报;其次,他们构建的模型仅能预报ZTD,而在实际应用中ZWD和ZHD均需要单独获取,这些模型预报的功能也有限。基于此,本文针对以往神经网络模型的缺点,提出一种新的神经网络模型,探讨其是否适用于对ZHD和ZWD的长期预报。
1、 神经网络模型构造模型 1.1 神经网络建模参数分析经验ZTD模型也叫无需实测气象参数的ZTD模型,虽然目前的大多数经验ZTD模型在构造原理上并不完全一致,但是这些模型总体上都是利用ZTD或气象元素的周期变化规律和格网插值原理而构造的。基于此,GNSS用户只需知道其所在位置和使用时间便可以获取他们需要的ZTD (或是ZHD和ZWD)。一方面,文献[7]指出ZTD受经度λ、纬度φ和高程h共同影响;另一方面,ZTD在时间上表现出明显的周期变化规律:在中纬度和高纬度地区,ZTD时间变化周期时间是一年;而低纬度地区ZTD周期时间为半年[11]。因此也需要考虑ZTD的周期性,通常用年积日DOY来描述ZTD的时间变化。
综上,ZTD是由λ、φ、h和DOY这4个参数共同决定的。这4个参数与ZTD的关系可以表示为两个非线性数学关系。其中,λ、φ、h和DOY为自变量,而ZHD和ZWD为两个独立的因变量。
1.2 模型设计本文采用的神经网络模型为反向传播神经网络(back-propagation neural network,BPNN)[12]。BPNN是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。BPNN属于有教师指导的学习方式,主要包括两个过程:正向传播输入信号从输入层经隐含层,传至输出层的过程;反向误差传播将误差从输出层反向传至输入层,并通过梯度下降算法来调节连接权值与偏置值的过程。BPNN可以学习和存储大量的输入-输出模式映射关系,而无需事前揭示、描述这种映射关系的数学方程。因此,BPNN可以处理复杂的非线性拟合的问题。因此,本文尝试使用BPNN来解释ZTD和4个变量(λ、φ、h和DOY)之间的关系。由于ZHD和ZWD变化规律区别较大,且GNSS用户在使用时也需要分别获取ZHD和ZWD。因此,本文在设计神经网络时构造了两个BPNN:BPNN_ZHD和BPNN_ZWD, 分别用于预报ZHD和ZWD。BPNN_ZHD和BPNN_ZWD模型构造见表 1。BPNN_ZHD和BPNN_ZWD输入均是DOY、λ、h、φ,输出分别为ZHD和ZWD。
| 模型 | 输入 | 隐含层 | 输出 |
| BPNN_ZHD | DOY,λ,h,φ | 神经元个数为3的单隐含层 | ZHD |
| BPNN_ZWD | DOY,λ,h,φ | 神经元个数为3的单隐含层 | ZWD |
本文选择欧洲地区及附近地区作为研究领域,其范围为:(35°N~60°N,-10°E~40°E)。
2.2 训练数据本文的训练数据是来自澳大利亚维也纳技术大学的GGOS Atmosphere数据[12]。GGOS Atmosphere数据可在网址http://ggosatm.hg.tuwien.ac.at/下载,GGOS Atmosphere可以提供丰富的对流层产品。这些数据是基于ECMWF (European Centre for Medium-Range Weather Forecasts)的40年再分析资料所提供的数据。训练数据选用位置如图 1中标记为“*”所示,数据基本信息见表 2。
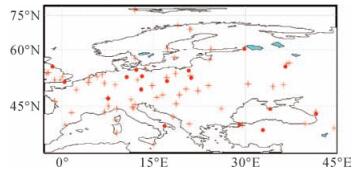
|
| 图 1 训练站和测试站分布 |
测试试验地点包含了欧洲范围及周边区域的18个IGS站,其分布如图 1中标记为“·”所示。数据信息见表 2。为了客观地体现模型的精度,测试数据是选择与训练数据不同的数据源且测试的位置和时间也与训练的数据不同。测试数据是IGS分析中心提供的ZTD产品(ftp://cddis.gsfc.nasa.gov/pub/gps/products/troposphere/zpd/)。对应的实测气象数据可以在网站ftp://cddis.gsfc.nasa.gov/pub/gps/data/daily/下载获取。目前,虽然全球已经有超过400个IGS站,但是能够提供实测气象参数的站却不到100个。IGS站ZTD产品可以作为近似真值,文献[13-14]的结果显示IGS的ZTD产品达到的精度为1.5~5 mm。ZHD的近似真值是根据Saastamoinen模型[15]计算得到的。Saastamoinen模型计算ZHD的精度可以达到亚毫米级,模型计算公式为
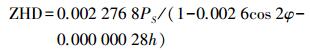 (2)
(2) 式中, PS为GNSS接收机天线位置的大气压力,单位为mbar;φ为纬度,单位为(°);h为高度,单位为m。那么,ZWD的近似真值的提取可以表示为
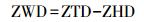 (3)
(3) 式中,ZHD是使用实测PS代入Saastamoinen模型计算值;ZTD是从IGS站提供的ZTD产品获取。
2.4 结果分析与比较本文将GPT2w模型计算结果作为精度参考值进行对比。GPT2w模型目前是精度最高的经验ZTD模型之一,其格网数据水平分辨率为1°,包括了一些与对流层延迟有关的气象元素的平均值、年周期和半年周期的参数。GPT2w模型计算ZHD的基础模型为式(2)的Saastamoinen模型。GPT2w模型计算ZWD的基础模型为
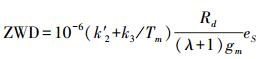 (4)
(4) 式中,k′2和k3是常系数;Rd是干空气的气体常数;eS是GNSS接收机天线位置的水汽分压,单位为mbar;Tm是加权平均温度;λ是水汽梯度因子;gm是重力系数,其计算式为
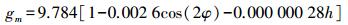 (5)
(5) Tm和λ的定义分别为
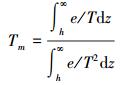 (6)
(6) 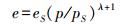 (7)
(7) 由于式(4)中k′2、k3和Rd是常系数,因此GPT2w模型提供Tm、λ和eS的经验值用于计算经验的ZWD,而提供的PS的经验值用于计算经验的ZHD。
本文使用平均偏差Bias和均方根误差RMSE两个指标来评估模型的精度。表 3和表 4分别是ZHD和ZWD精度。整体来说,神经网络预报的结果误差仅与GPT2w模型预报的结果相差4.0%和2.6%,因此神经网络预报的ZHD精度和ZWD精度与GPT2w模型相当。从单站的精度来看,所有测试站的精度均与GPT2w相当,未出现较大的偏差。因此,本文提出的神经网络模型预报ZHD和ZWD均已经获取较高精度,而且,文中测试数据的时间范围是2010-2014年,可以看出该模型在长达5年时间内仍然可以保持较好的精度。
| mm | |||||
| 测试站 | GPT2w | BPNN_ZHD | |||
| Bias | RMSE | Bias | RMSE | ||
| 所有站 | 0.1 | 19.0 | -3.7 | 19.8 | |
| MORP | 2.4 | 29.1 | 4.5 | 29.2 | |
| HERT | -0.5 | 22.8 | -4.8 | 23.4 | |
| HERS | 1.6 | 22.7 | -2.9 | 22.9 | |
| ZIMM | -0.8 | 15.3 | -9.2 | 18.2 | |
| PTBB | 0.7 | 19.4 | -4.2 | 20.0 | |
| WARN | -0.1 | 20.3 | -3.3 | 20.6 | |
| WTZR | -0.9 | 16.2 | -8.2 | 18.3 | |
| POTS | -5.4 | 18.4 | -10.6 | 20.5 | |
| MATE | -1.0 | 13.3 | -4.1 | 14.2 | |
| WROC | -1.3 | 17.3 | -7.5 | 19.1 | |
| LAMA | -0.4 | 19.3 | -2.2 | 19.6 | |
| JOZE | -3.1 | 18.7 | -7.7 | 20.2 | |
| ISTA | 2.4 | 13.3 | -4.3 | 14.7 | |
| SVTL | 0.0 | 25.4 | 2.6 | 25.4 | |
| ANKR | 2.3 | 10.8 | -1.3 | 12.3 | |
| CRAO | 0.8 | 12.8 | -2.2 | 13.9 | |
| MOBN | -1.5 | 27.1 | -3.4 | 27.1 | |
| ZECK | 2.1 | 10.8 | -2.3 | 10.9 | |
| mm | |||||
| 测试站 | GPT2w | BPNN_ZWD | |||
| Bias | RMSE | Bias | RMSE | ||
| 所有站 | -0.1 | 33.3 | -0.6 | 34.2 | |
| MORP | 1.7 | 31.2 | -7.9 | 32.6 | |
| HERT | 4.7 | 36.2 | -1.7 | 36.7 | |
| HERS | -0.7 | 36.0 | -7.0 | 37.5 | |
| ZIMM | 0.2 | 27.4 | -5.9 | 28.9 | |
| PTBB | -4.7 | 35.8 | -10.0 | 37.0 | |
| WARN | 2.3 | 35.6 | -0.3 | 35.7 | |
| WTZR | 0.2 | 29.0 | -3.3 | 29.4 | |
| POTS | 4.7 | 37.8 | 0.8 | 38.0 | |
| MATE | 0.5 | 31.1 | 6.2 | 33.7 | |
| WROC | 0.5 | 35.2 | -3.4 | 35.4 | |
| LAMA | -0.6 | 34.2 | -1.1 | 34.0 | |
| JOZE | -1.6 | 35.0 | -4.3 | 35.3 | |
| ISTA | -3.9 | 35.7 | 4.0 | 36.9 | |
| SVTL | 0.9 | 31.8 | 1.3 | 32.1 | |
| ANKR | -1.3 | 28.0 | 9.5 | 30.7 | |
| CRAO | -5.0 | 34.5 | 8.8 | 35.6 | |
| MOBN | 3.0 | 27.6 | 2.8 | 28.0 | |
| ZECK | 4.8 | 25.9 | 1.7 | 25.0 | |
但是,GPT2w模型需要1°水平网格的外部数据。由于当计算ZWD时,GPT2w模型需要计算水汽压力、加权平均温度、水汽梯度影响因子等气象元素的格网参数,可知GPT2w模型不仅需要准备大量的计算数据而且计算过程也相对比较复杂。本文设计的神经网络模型仅仅需要两个训练完毕的模型,即可以实现分别预报不同位置和不同时段的ZHD和ZWD。
因此,从综合考虑的角度来看,本文提出的基于神经网络模型的经验ZTD模型,不仅能较好地长期预报ZHD和ZWD,而且比经验ZTD具有更好的适用性。
3、 结论与展望针对经验ZTD模型与神经网络在ZTD应用中的不足,本文提出了基于神经网络的经验ZTD模型。试验结果表明,本文提出的神经网络模型具有良好的精度。相比于传统的神经网络模型而言,本文模型的优点是不仅能够单独预报ZHD和ZWD,而且也适合长期预报。与精密格网的经验ZTD模型相比,本文构造的神经网络模型使用更为简单,并且在使用前无需准备大量数据,因此,该模型在GNSS领域值得推广应用。
| [1] | PENNA N, DODSON A, CHEN W. Assessment of EGNOS Tropospheric Correction Model[J]. The Journal of Navigation, 2001, 54(1): 37–55. DOI:10.1017/S0373463300001107 |
| [2] | KOUBA J. Testing of Global Pressure/Temperature (GPT) Model and Global Mapping Function (GMF) in GPS Analyses[J]. Journal of Geodesy, 2009, 83(3-4): 199–208. DOI:10.1007/s00190-008-0229-6 |
| [3] | LAGLER K, SCHINDELEGGER M, BÖHM J, et al. GPT2:Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069–1073. DOI:10.1002/grl.50288 |
| [4] | 王勇, 张立辉, 杨晶. 基于BP神经网络的对流层延迟预测研究[J]. 大地测量与地球动力学, 2011, 31 (3) : 134–137. |
| [5] | SCHVLER T. The TropGrid2 Standard Tropospheric Correction Model[J]. GPS Solutions, 2014, 18(1): 123–131. DOI:10.1007/s10291-013-0316-x |
| [6] | YAO Y, XU C, SHI J, et al. ITG:A New Global GNSS Tropospheric Correction Model[J]. Scientific Reports, 2015(5): 10273. |
| [7] | 李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57 (15) : 1317–1325. |
| [8] | 姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56 (7) : 2218–2227. |
| [9] | HAYKIN S. Neural Networks:A Comprehensive Foundation[J]. New Jersey:IEEE, 2010. |
| [10] | 尹为松, 陶庭叶, 邓清军, 等. 遗传算法优化的GPS对流层延迟内插算法[J]. 测绘科学, 2016, 41 (1) : 180–184. |
| [11] | JIN S, PARK J, CHO J, et al. Seasonal Variability of GPS-derived Zenith Tropospheric Delay (1994-2006) and Climate Implications[J]. Journal of Geophysical Research Atmospheres, 2007, 112(D9): 139–155. |
| [12] | 姚宜斌, 胡羽丰, 余琛. 一种改进的全球对流层天顶延迟模型[J]. 测绘学报, 2015, 44 (3) : 242–249. |
| [13] | DOW J M, NEILAN R E, RIZOS C. The International GNSS Service (IGS):Preparations for the Coming Decade[C]//20th Int Tech Meeting of the Satellite. Fort Worth, Texas:Division of the US Inst of Navigation, 2007:25-28. |
| [14] | DOW J M, NEILAN R E, GENDT G. The International GPS Service:Celebrating the 10th Anniversary and Looking to the Next Decade[J]. Advances in Space Research, 2005, 36(3): 320–326. DOI:10.1016/j.asr.2005.05.125 |
| [15] | SAASTAMOINEN J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[J]. The Use of Artificial Satellites for Geodesy, 1972, 15(6): 247–251. |
| [16] | BÖHM J, MÖLLER G, SCHINDELEGGER M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433–441. DOI:10.1007/s10291-014-0403-7 |
| [17] | LEANDRO R F, LANGLEY R B, SANTOS M C. UNB3m_pack:A Neutral Atmosphere Delay Package for Radiometric Space Techniques[J]. GPS Solutions, 2008, 12(1): 65–70. DOI:10.1007/s10291-007-0077-5 |
| [18] | SUPARTA W, ALHASA K M. Application of ANFIS Model for Prediction of Zenith Tropospheric Delay[C]//20133rd International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering (ICICI-BME).[S.l.]:IEEE, 2013:172-177. |
| [19] | SUPARTA W, ALHASA K M. Prediction of ZTD Based on ANFIS Model[C]//Modeling of Tropospheric Delays Using ANFIS.[S.l.]:Springer International Publishing, 2016:85-107. |
| [20] | 胡伍生. 神经网络理论及其工程应用[M]. 北京: 测绘出版社, 2006. |



