随着GNSS技术的发展与完善,多个国家、地区、行业纷纷建立了满足自身需求的连续运行GNSS基准站网[1]。随着基准站网数量的不断增加,其数据处理方法也越来越引起人们的重视。如何形成一套有效的数据处理策略,在保证解算精度与可靠性的前提下节省解算时间和存储空间,一直是人们所研究的重点[2]。
将全部测站、所有时段的观测数据一并处理虽可保证数学模型的严密性,但仍存在诸多难点。如目前全球公认的高精度GNSS数据解算软件GAMIT、GIPSY、Bernese、EPOS等中,GAMIT只能解算不超过100个测站的数据[3],Bernese、EPOS等虽可同时解算100个以上测站的数据,但解算时间过长,占用内存较多。为解决上述问题,目前常用的参数估计方法一般分3步完成:①将整个观测网分为若干子网,将各个子网、各个时段的观测数据单独解算得到松约束下的参数估值及其方差-协方差矩阵;②结合所有松约束结果得到站坐标、速度场、地球自转参数及卫星轨道等的统一估值;③根据外部信息引入基准,得到参数最终估值[4]。此算法大幅节省了计算时间,也可最大限度地保证理论严密。上述步骤②一般通过法方程叠加完成。法方程叠加的本质为序贯最小二乘,理论严密,且省略诸多矩阵求逆运算,效率较高。以基线向量为虚拟观测值,施闯研究了基于法方程叠加的大规模GNSS网平差方法,并编制了相关软件[5]。姚宜斌研究了坐标模式的法方程叠加方法,推导了相应公式,对各类参数的估计方法进行了总结[6-7]。但法方程叠加法对状态参数的处理较复杂。起源于20世纪60年代的Kalman滤波理论将状态空间的概念引入到随机估计问题中,把信号过程视为白噪声作用下线性系统的输出,并用状态方程描述这种关系,可方便处理状态参数,且不需存储中间过程,大幅节省了存储空间,可有效地应用于GNSS基准站网数据处理[8]。
本文以Kalman滤波理论为基础,研究滤波算法在大规模GNSS网参数(测站坐标、卫星轨道、极移参数等)估计中的作用,并根据实测数据对方法进行验证。结果表明,利用Kalman滤波理论可以高精度、高效率地进行GNSS网各类参数的估计。
1、 参数估计方法采用Kalman滤波算法进行参数估计,首先应根据未知参数的先验信息及状态方程预测下一时刻的参数估值及其方差-协方差矩阵;再以下一时刻所有子网在基线解算阶段所得参数估值及其方差-协方差阵为虚拟观测值对预测值进行修正,并根据修正后的参数信息预测下时刻的状态。该过程循环渐进,依次进行,直至所有信息均考虑在内。利用Kalman滤波算法结合多个子网的松约束结果与结合多个时段的解算结果方法类似,实际上前者可看作是后者在时段间隔为0时的特殊情况。
假设δlk=lk-l0k为tk时刻线性化后的准观测值向量。其中l0k为外部提供的参数先验信息;lk为基线解算阶段所得参数估值。则观测方程为
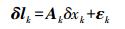 (1)
(1) 式中,δxk为待估参数向量,包含所有测站位置参数、所有参与解算卫星轨道参数,以及各测段中间历元的ERP参数及其线性速度;Ak为设计矩阵;εk是方差为Pk的零均值噪声向量。状态方程为
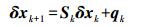 (2)
(2) 式中,Sk为状态转移矩阵;qk为方差为Qk的随机过程噪声向量。为估计tk+1时刻的状态,首先预测tk+1时刻的参数估值及其方差-协方差阵
 (3)
(3) 式中,Ck为基线解算阶段所得参数估值的方差-协方差矩阵。
然后利用虚拟观测值对预测的参数状态进行修正
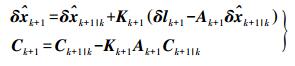 (4)
(4) 其中
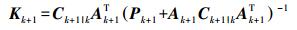 (5)
(5) 上述即为利用Kalman滤波进行GNSS网参数估计的过程,其流程如图 1所示。
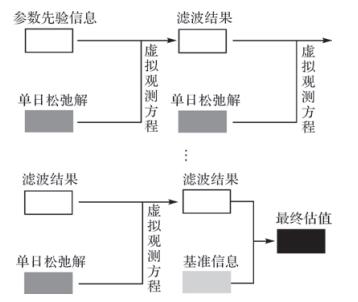
|
| 图 1 基于Kalman滤波的参数估计流程 |
在Kalman滤波过程中,滤波起始阶段的先验信息对于滤波是否收敛及收敛速度具有重要影响。在GNSS网参数估计中,一般选取基线解算阶段所得参数估值为先验值启动滤波器。滤波时需在状态方程中加入随机过程噪声以削弱诸如测站震后蠕变、天线高量测误差、ERP参数变化等的影响。随机游走过程(random walk process,RWP)较多地被应用其中。测站坐标的随机游走噪声参数需根据各测站数据采集过程中的具体情况确定。根据IERS的结果,极移的随机游走噪声方差一般可设为22.8 mas2/a,表示允许极移参数每天变动0.25 mas。结果表明,允许时段之间参数的随机变化可有效吸收模型误差及测站位置变动等对估计结果的影响,提高状态参数的估值精度[9]。
为消除各时段/子网解之间的系统误差,需在滤波函数模型中通过扩充状态空间引入系统误差参数。系统误差可分为位置基准的系统误差、时间演变基准的系统误差、尺度基准的系统误差和空间方位基准的系统误差4类。对于粗差可用残差加权平方和进行探测。残差的加权平方和定义为
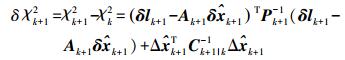 (6)
(6) 其中
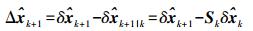 (7)
(7) 滤波过程中每步均计算残差加权平方和,若其超限则说明基线解算阶段所得参数估值中可能含有粗差,或对参数的先验约束过紧。经验表明,残差加权平方和的限差设为100较为适宜。
若在滤波起始阶段对参数的约束较松,则滤波完成后得到的结果是一无约束或松约束网形,需引入外部信息,以确定整网基准[10]。对测站位置基准的定义可通过HERMERT参数转换的方法实现。该方法最大限度地保留了GNSS观测的原始精度,防止引入的基准信息误差破坏参数估计结果。已有研究表明,利用Helmert参数转换的方法定义基准在只估计3个旋转参数的情况下GNSS网形不发生任何变化;若同时顾及3个平移参数会导致网形畸变,但对上万千米的基线,畸变量在3 mm以内[11]。
2、 数据分析为验证上述理论结果,本文利用实测数据进行了试验。文中基线解算采用GAMIT软件完成。
2.1 方案设计本文采用的数据为2013年1月1日(年积日1)至2月19日(年积日50)全球均匀分布的40个IGS跟踪站的观测数据,站点分布如图 2所示。文中将40个跟踪站分为两个子网分别进行基线解算。子网1包含26个测站(图 2中灰色点与黑色点);子网2包含25个测站(图 2中灰色点与浅灰色点)。两个子网拥有11个公共站点(图 2中灰色点)。公共站点基本均匀分布于全球,用于滤波时联结两个子网的解算结果。
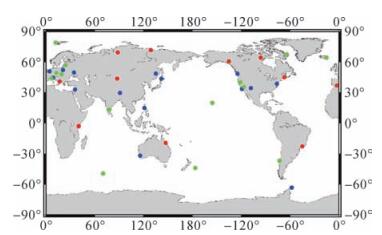
|
| 图 2 测站分布 |
基线解算阶段的参数设置见表 1。
基线解算时为防止先验信息不准确引入误差,对各类参数的约束均较松,导致结果整体存在平移、旋转和缩放,在滤波时需根据参数的先验信息确定基准。滤波以基线解算所得100个单日松弛解为对象,将其作为准观测值输入滤波器。
2.2 结果分析本文主要通过Kalman滤波实现测站位置参数、卫星轨道参数、极移参数等的估计。
估计测站位置参数时以两个子网的100个单日松弛解为输入。由于对测站位置的估计可利用Helmert转换的方式引入基准,故Kalman滤波时测站位置、卫星轨道、ERP参数的先验约束均松弛,以滤波不发散为目的。Helmert转换中用于基准定义的测站为图 2中11个公共站点,基准测站坐标采用IGS公布的结果。本文以IGS结果为准检验其余测站位置估值精度。
图 3为各测站坐标分量估值与IGS结果之差(不包括11个公共站点)。由图 3可看出,本文对测站位置参数的估值精度较高;各测站坐标分量与IGS结果的较差基本在2 cm以内。统计结果显示,各分量较差均值分别为0.24、0.35、-0.14 cm,RMS值分别为0.85、1.1、1.21 cm。
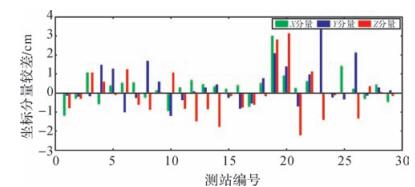
|
| 图 3 测站坐标估值与IGS结果之差 |
估计卫星轨道参数时可以广播星历为先验值。为防止轨道估计的“末端效应”,本文利用年积日1日至3日连续3天共6个单日松弛解文件估计卫星轨道,并取2日的轨道与IGS轨道对比以检验参数估计精度。在基线解算阶段所有3天的卫星轨道参数均为中间一天中间时刻的密切元素以及太阳光压、Y轴偏差等。在滤波过程中紧约束测站位置及ERP参数,以提供基准。测站坐标的先验值采用IGS的结果,ERP参数的先验值采用IERS的结果。
图 4为作为初始值的广播星历与IGS轨道在参考时刻之差。图 5为估计的卫星轨道参数外推1小时得到的卫星位置与IGS轨道之差。与IGS精密星历相比,本文所得轨道在3个方向的较差均值分别为-0.6、-0.9、-1.1 cm;各分量较差的RMS值分别为9.8、8.6、7.2 cm。作为初始值的广播星历3个方向的较差均值分别为5.2、-5.1、11.5 cm;各分量较差的RMS值分别为66.6、77.8、60.7 cm。由此可知,利用Kalman滤波,融合多天观测数据以估计卫星轨道的方法大幅提高了轨道精度。本文的主要目的为方法验证,因此采用的测站数目与观测时间有限。可以预见,如果利用更多测站、更长的观测时间估计卫星轨道,应该可以得到更好的结果。

|
| 图 4 广播星历与IGS精密星历之差 |
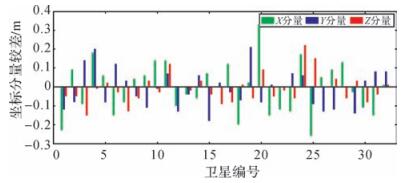
|
| 图 5 卫星轨道估值与IGS精密星历之差 |
ERP参数是不断变化的,因此本文每天估计一套对应于测段中间历元的ERP参数。在估计ERP参数时需对测站位置及卫星轨道紧约束。同时,由于日长变化(length of day,LOD)与卫星轨道的升交点赤经Ω强相关,因此利用GNSS技术不能实现LOD的直接估计。本文仅针对极移参数进行分析。
图 6为极移估值与IERS所公布结果的较差。由图 6可知,本文所得极移参数估值与IERS结果之差基本在0.1 mas以内,约对应地球表面赤道处3.1 mm的位移,精度较高。但由图 6可知估值存在系统误差,原因尚需进一步分析。

|
| 图 6 极移参数估值与IERS结果之差 |
随着GNSS技术的发展,其逐渐成为获取各类参数的重要手段。本文主要研究了利用Kalman滤波结合多个子网、多个时段的松弛解文件进行大规模GNSS网参数估计的理论,并通过实测数据对方法进行了验证。结果表明,利用Kalman滤波技术可进行地面测站位置参数、导航卫星轨道参数及地球自转参数(主要为极移参数)的高精度估计,从而为利用GNSS技术估计各类参数提供了一种有效的技术手段,可以在科研生产中推广应用。
| [1] | 李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009. |
| [2] | 杨凯.大规模GNSS基准站网数据处理关键技术研究与实现[D].武汉:武汉大学, 2011. |
| [3] | MIT. GAMIT Reference Manual Release 10.4[EB/OL].[2014-11-15].http://www-gpsg.mit.edu/~simon/gtgk/GAMIT_Ref.pdf. |
| [4] | DONG D, HERRING T A, KING R W. Estimating Regional Deformation from a Combination of Space and Terrestrial Geodetic Data[J]. Journal of Geodesy, 1998, 72(4): 200–214. DOI:10.1007/s001900050161 |
| [5] | 施闯. 大规模高精度GPS网平差与分析理论及其应用[M]. 北京: 测绘出版社, 2002. |
| [6] | 姚宜斌, 刘经南, 陶本藻, 等. 基于坐标模式的广义网平差模型研究[J]. 武汉大学学报(信息科学版), 2006, 31 (1) : 16–18. |
| [7] | 姚宜斌. GPS精密定位定轨后处理[M]. 北京: 测绘出版社, 2008. |
| [8] | 付梦印, 邓志红, 闫莉萍. Kalman滤波理论及其在导航系统中的应用[M]. 2版. 北京: 科学出版社, 2010. |
| [9] | HERRING T A, DAVIS J L, SHAPRIO I I. Geodesy by Radio Interferometry:The Application of Kalman Filtering to the Analysis of Very Long Baseline Interferometry Data[J]. Journal of Geophysical Research, 1990, 95(B8): 12561–12581. DOI:10.1029/JB095iB08p12561 |
| [10] | HEFLIN M, BERTIGER W, BLEWITT G, et al. Global Geodesy Using GPS without Fiducial Sites[J]. Geophysical Research Letters, 1992, 19(2): 131–134. DOI:10.1029/91GL02933 |
| [11] | 肖玉钢, 刘鸿飞, 王峥. GNSS网参数估计中基准定义方法研究[J]. 大地测量与地球动力学, 2012, 32 (4) : 79–82. |
| [12] | DONG D, BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research, 1989, 94(B4): 3949–3966. DOI:10.1029/JB094iB04p03949 |
| [13] | SCHMID R, ROTHACHER M, THALLER D, et al. Absolute Phase Center Corrections of Satellite and Receiver Antennas[J]. GPS Solutions, 2005, 9(4): 283–293. DOI:10.1007/s10291-005-0134-x |


