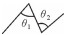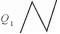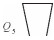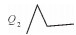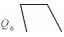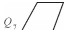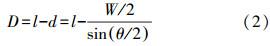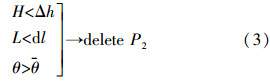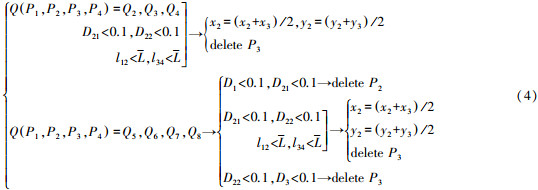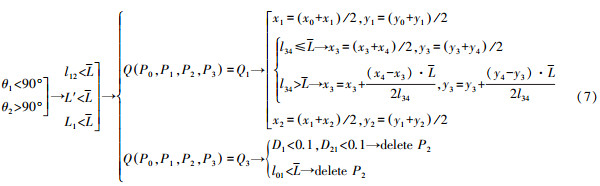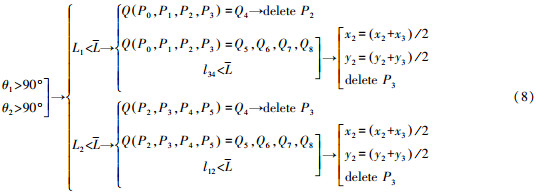随着由库到图的制图技术越来越成熟,新版《国家普通地图集》采用国家1:100万基础地理信息数据库作为制图数据进行缩编成图。然而,从百万比例尺缩编成几百万,甚至是千万比例尺的地图,不可避免地面临着线要素综合问题。其中,线要素简化是线要素综合的核心问题。
目前,国内外已有很多关于线要素简化方面的研究。其中较著名的有Douglas算法[1],该方法通过判断曲线节点与直线的距离是否小于给定的阈值,从而达到数据简化的目的,如果小于,则剔除节点。为了弥补Douglas算法在简化过程中损失的信息,Tong等利用最小二乘理论,提出了一种不确定性过程模型,避免了简化后曲线长度、面积等信息的失真[2]。Li等受启发于自然界中所观察到的自然综合过程原理,提出了一种自适应线状要素综合算法,该方法利用最小可见目标尺寸作为曲线细节信息删除与否的阈值,以达到简化的目的[3]。针对Li-Openshaw算法的不足,朱鲲鹏等利用局部极大值点[4]、黄志坚等利用角点检测器筛选出的关键点[5],将曲线在特征点处分段,每段再用Li-Openshaw进行简化,从而更好地保持了曲线整体形状。
近年来,学者们探寻出了一条利用弯曲识别来达到线要素简化的新思路。艾廷华利用约束的Delaunay三角网模型提出了一种曲线弯曲特征的深度层次结构,实现了大弯曲套小弯曲层次结构的表达[6]。毋河海通过多次应用矢量叉积乘积,结合曲线光滑原理,以寻找曲线的最或然拐点[7]。罗广祥利用坐标非单调性变化产生线状地图要素弯曲的认知模型,并通过顺序比较坐标大小来识别地图弯曲[8]。郭庆胜从视知觉的角度,综合利用曲线的极值点、拐点、迂回曲线分界点、方向扰动奇异点来识别弯曲[9]。操震洲以曲线轴线作为弯曲划分基准,通过递归方式层次化提取不同方向、不同区间上的弯曲[10]。
不置可否,目前所见文献对线要素简化有一定的研究意义,但现有处理方法所获得的简化结果较难令人满意,以至于在制图过程中,人们往往更愿意采用手工为主的方式对线要素进行简化,原因有以下几点:
1) 就制图而言,线要素简化不仅要减少节点,保持弯曲特征,还要考虑地图出版印刷等问题。
2) 针对不同类型、比例尺的线要素,阈值较难保证统一,从而导致方法的适用性不高。
3) 仅利用弯曲识别较难获得满意的结果,还需要对弯曲进行分类,因为不同类型的弯曲处理方式不同。
综上所述,如何提出一种能够处理多类型线要素,且能与手工处理结果相接近的简化方法,已成为《国家普通地图集》迫切需要解决的问题[3]。为此,本文提出一种深度简化方法,该方法将线要素简化分解成若干子过程,各个子过程通过弯曲识别与分类,并根据自适应或符合视觉认知的阈值进行组合,处理不同类型的弯曲。
一、弯曲分类与简化阈值 1. 弯曲分类假设两线段组成的弯曲为一级弯曲,三线段组成的弯曲为二级弯曲。
由于一级弯曲是最底层弯曲,具有普遍性,因此一级弯曲的可分类性不高,本文重点在于二级弯曲的分类。根据二级弯曲中是否存在拐点,可将其分为两大类。其中拐点存在与否可利用式(1)来判断[7],即
结合下文中的弯曲夹角θ,又可将每个大类分成4小类,具体见表 1。
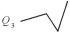
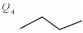
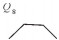
令Q(P1,P2,P3,P4)为弯曲识别函数,P为输入的节点,其值域为Q1~Q8。由表 1可知,任何节点数大于4的线要素都是由二级弯曲组合而成的。
2. 简化阈值为了判断二级弯曲在何种情况下需要处理,阈值是个不可避免的问题,其定义如下:
1) 弯曲口长L[11]:一级弯曲中,首尾节点之间的距离,如图 1所示。
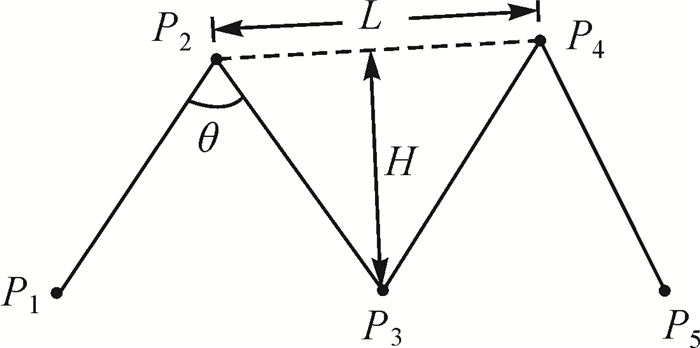 |
| 图 1 一级弯曲上的简化阈值 |
2) 弯曲深度H[11]:一级弯曲中,中间节点到首尾节点所在直线的距离,如图 1所示。
3) 弯曲夹角θ:一级弯曲中,两线段的夹角,其中0 < θ < 180°,如图 1所示。
4) 拐线长度L′:二级弯曲中间线段的长度。
5) 平均线段长度L:曲线上所有线段的平均值。
6) 平均弯曲夹角θ:曲线上弯曲夹角的平均值。
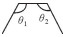
7) 弯曲重叠度D:因线宽导致的曲线在转角处产生重叠与相邻线段的差值,如图 2所示,其中
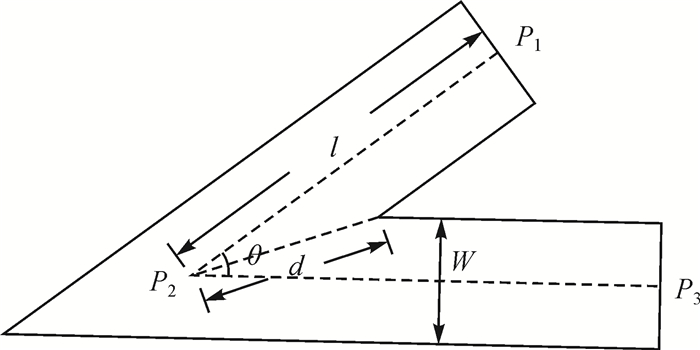 |
| 图 2 弯曲重叠度 |
式中,W为线宽。需要说明的是二级弯曲的拐线有两个弯曲重叠度。
二、线要素深度简化简化目标:在保证弯曲特征的情况下,使原始线要素禁锢在结果线要素的线宽范围内,且尽可能使原始线要素处于结果线要素的中间,如图 3所示,黑色为原始线要素。灰色为简化结果线要素。
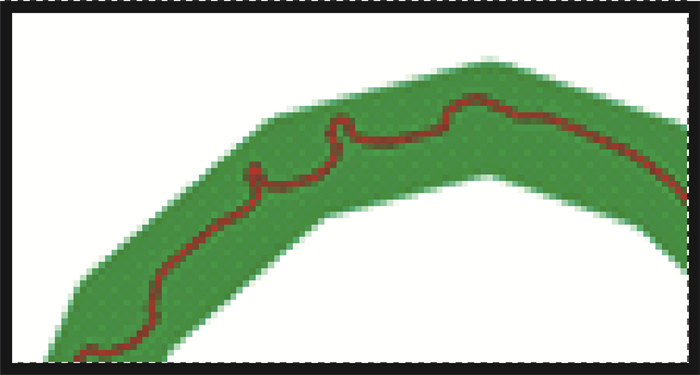 |
| 图 3 简化目标 |
简化思想:如果仅将线要素分成一级弯曲来处理,很难得到满意的结果,因为一级弯曲之间的关联性很强,处理一级弯曲时,会对其相邻的一级弯曲造成破坏。虽然二级弯曲之间的关联性较弱,但如果将弯曲对象仅局限于单个的二级弯曲,也较难获得满意的结果,因为在线要素节点环境非常复杂的情况下,往往存在单个二级弯曲的处理是模糊的情况,即使人工都难以决策。而且在线要素简化的过程中,线要素上各个一、二级弯曲的尺寸是逐渐变大的。
基于此,深度简化方法应运而生。该方法将线要素的简化过程剥离成多个子过程,每个子过程处理不同类型的弯曲,且每个子过程的阈值组合随着弯曲类型的不同而不同。具体如下:
1. 重点剔除输入节点P1、P2,计算点间距l12,若l12 < Δl,则删除节点P1或P2,并进行迭代,直到没有新点删除为止。
2. 第1层简化考虑到当比例尺相差较大时,如从百万数据库到千万比例尺图的缩编过程,线要素上的节点数量是非常巨大的,因此需要首先对一级弯曲进行处理,为下层简化减轻负担。假设输入节点(P1,P2,P3),计算弯曲深度、弯曲口长和弯曲夹角,利用如下阈值组合,判断是否处理当前弯曲
式中]表示“并”,下同。式(3)表明,当弯曲深度小于Δh、弯曲口长小于dl,且弯曲夹角小于平均弯曲夹角时,一级弯曲近似于线段,故删除节点P2。
迭代上述过程,直到没有新点删除为止。如图 4(a)所示。
 |
| 图 4 深度简化过程 |
该层简化主要对独立的二级弯曲进行处理。假设输入节点(P1,P2,P3,P4),首先利用式(2)计算该二级弯曲首尾两线段的弯曲重叠度D1、D3,以及拐线的弯曲重叠度D21、D22,然后根据二级弯曲的类型,进行如下处理
式中{表示“或”,下同。由式(4)可知,当弯曲类型为Q2~Q8时,判断D21、D22是否小于0.1 mm。若两者都小0.1 mm,说明拐线很短,在视觉上会被相邻线段淹没掉。此时,若l12、l34均小于平均点间距,那么移动节点P2,并删除节点P3。
若弯曲类型为Q5~Q8时,判断D1、D21是否小于0.1 mm。若相邻两线段的弯曲重叠度均小于0.1 mm,那么在视觉上两线段近似重合。此时,需要删除节点P2。同理,当D22、D3均小于0.1 mm时,删除节点P3。
由于线要素的节点环境对于计算机而言是未知的,在某些情况下,式(4)的判断会无效,但是拐线在视觉上仍然会被淹没掉,主要原因是L′ < W,因此在这种情况下,需根据式(5)来处理弯曲
式中,n为显著系数。由式(5)可知,当存在L′ < W的情况时,首先判断l12与l34的关系,如果l12明显比l34长,那么删除节点P3,反之删除节点P2。如果两者长度对比不明显,就移动节点P2,并删除节点P3。迭代上述过程,直到没有新点删除为止,如图 4(b)所示。
4. 第3层简化实际上,第2层简化能够对大部分独立二级弯曲进行处理,但在某些情况下,独立二级弯曲的处理是模糊的,即使人工都难以判断,因此需要对独立二级弯曲进行延伸,以作为辅助判断来决定当前二级弯曲处理方式。
假设输入节点(P0,P1,P2,P3,P4,P5),(P1,P2,P3,P4)为当前二级弯曲,P0、P5为延伸点,从而将独立的二级弯曲延伸为3个相邻的二级弯曲。
1) 若当前弯曲类型为Q1,弯曲的处理方式见式(6)
式(6)表明,为了控制弯曲的处理长度,保证曲线特征,首先比较l12、L′及第1个弯曲口长L1与平均点间距L的大小,若都小于L,继续判断Q(P0,P1,P2,P3)的弯曲类型,若为Q1,则直接移动节点P2,同时根据l12与l34的关系,移动节点P3;若当前二级弯曲的前后相邻的二级弯曲为Q2和Q5~Q8,则删除节点P2。同理,比较L′、l34及第2个弯曲口长L2与L的关系,进行同样过程的处理。最后,若拐线较短,且二级弯曲首尾线段较长,即比较l12、L′、l34与L的大小,若符合式(6),则移动节点P2,并删除节点P3。
2) 若当前弯曲类型为Q2时,弯曲的处理方式见式(7),需要说明的,弯曲类型Q3与Q2处理方式一致。
根据式(7),首先判断l12、L′、L1与L的关系,若均小于,则判断Q(P0,P1,P2,P3)是否为Q1,若是,则移动节点P1和P2。为处理节点P3,还需判断l34与L的大小,若l34小于L,可认为l34很短,则根据两节点坐标平均值移动节点;否则,认为l34较长,直接根据坐标平均值会影响简化的效果,故利用l34与的比值关系来移动节点P3。若Q(P0,P1,P2,P3)为Q3,则先判断D1和D21是否小于0.1 mm,若是,则删除节点P2;否则,为剔除无意义的突起弯曲,再判断l01是否小于L,若是,则删除节点P2。
3) 若当前弯曲类型为Q4时,弯曲的处理方式见式(8)。
根据式(8),首先判断L2是否小于L,若是,再判断Q(P0,P1,P2,P3)是否为Q4,若是,则删除节点P2。若Q(P0,P1,P2,P3)没有拐点,且l34小于平均点间距,那么移动节点P2,并删除节点P3,当L2 < L时,弯曲的处理方式与L1 < L一致。
迭代上述过程,直到没有新点删除为止。如图 4(c)所示。
需要说明的是:
1) 在线要素深度简化的过程中,平均点间距的作用是控制弯曲的长度,保证弯曲特征。
2) 式(5)—式(8)中,部分节点有的根据坐标均值来移动,有的根据线段比值关系来移动。主要是考虑到当线段明显较短时,可以直接用坐标均值的方式移动节点,而当线段明显较长时,如果用坐标均值的方式移动节点,会导致简化后的线段偏离原始线段,这就背离了上文阐述的“简化目标”,因此需要根据线段的比值关系来移动节点。
图 4中,黑色为原始线要素,灰色为各子过程简化后的线要素。
三、试验结果与分析 1. 阈值赋值1) 对于重点剔除过程中的Δl取值,试验中将其赋值为0.000 1 mm。需要说明的是,Δl取值不固定,只要认为两点的点间距小于Δl,就视为重点即可,但该值一定不能为0,因为计算机的浮点计算是有精度的。
2) 对于式(3)中的Δh、dl的取值,根据图上最小可视距离[11]为0.3~0.6 mm。试验中将dl取值为0.3 mm。同时,考虑到线宽是线要素一个非常重要的制图因子,试验中将Δh取值为线宽的1/4。因此,当一级弯曲满足式(3)的阈值组合时,可用直线代替一级弯曲,达到简化的目的。
3) 对于式(5)中的显著系数n,可取值为1.5,因为当线段A的长度大于线段B的1.5倍时,可视为线段A明显长于线段B。
4) 弯曲重叠度的赋值,主要考虑到线段在视觉上是否会被淹没等情况。一般情况下取值为0.1,即当两线段间距小于0.1 mm时,可视为两线段重合。
5) 其他阈值在简化过程中是自适应的,与平均点间距、平均弯曲夹角有关。
2. 简化试验试验数据来源于国家百万数据库。
1) 同线宽不同比例尺下的深度简化试验,见图 5、表 2,线宽为0.2 mm,黑色细线为原始线要素。
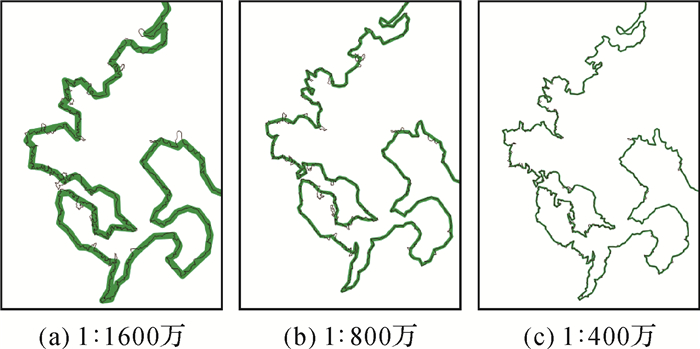 |
| 图 5 不同比例尺线要素的深度简化 |
2) 同比例尺不同线宽的深度简化试验,见图 6、表 3,线要素的比例尺为1:800万。
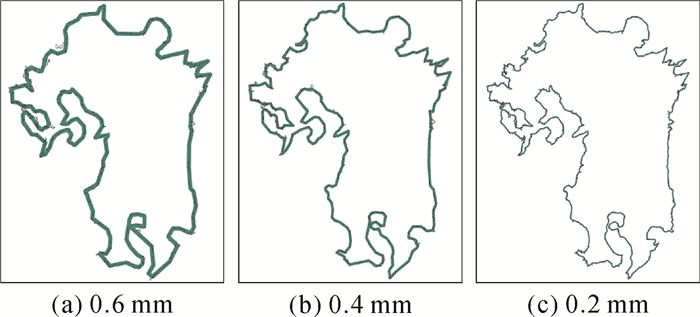 |
| 图 6 不同宽度线要素的深度简化 |
3) 不同类型要素的深度简化试验,如图 7所示,包括岛屿、境界线、道路、海岸线。
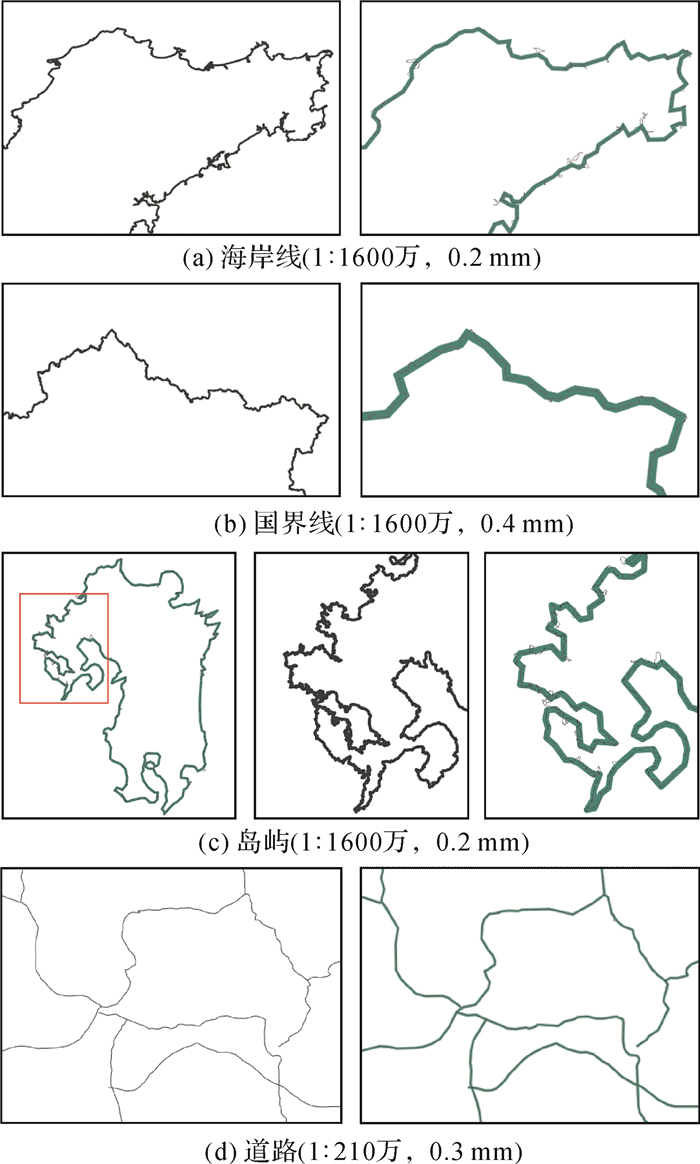 |
| 图 7 不同型线要素的深度简化 |
4) 与其他简化方法的对比试验,见图 8、表 4,线宽为0.2 mm,比例尺为1:1600万。
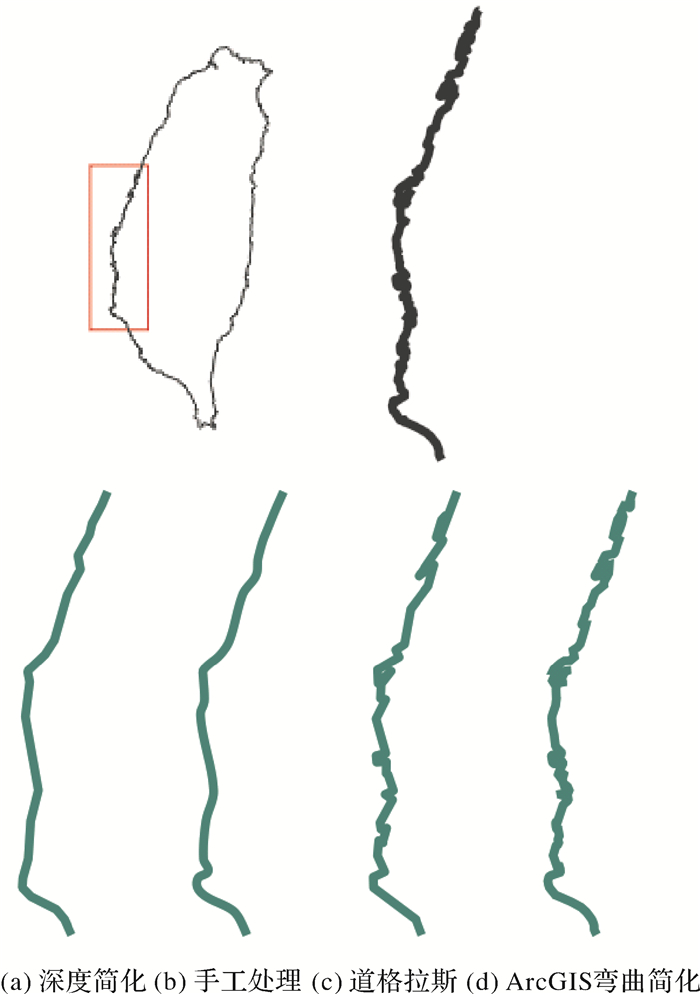 |
| 图 8 不同简化方法对比 |
1) 根据图 5和表 2,在线宽相同的条件下,随着比例尺的增大,深度简化能够保留线要素更多的细节,相应的,线要素的节点也会增加;反之,会剔除多余弯曲,使节点更少。这与客观认识是相符合的,因为对同一要素而言,比例尺越大,范围就越大,有意义的信息就会越多,就越能看清要素的细节部分;反之,能看到的细节就越少。
2) 根据图 6和表 3,在比例尺相同的情况下,随着线宽的减小,深度简化能够保留线要素更多的细节,相应的,线要素节点就会增加;反之,会剔除无意义细节,使节点更少。这与客观认识是相符合的,因为,线宽越小,弯曲之间的影响就越小,能够显示的细节就越多,反之,细节会被淹没。
3) 根据图 7,深度简化能够适应于多种不同类型的线要素简化。但各类型线要素的简化结果并非是相同的。其中,道路简化的效果最好,简化后,几乎不用人工再参与;相比较而言,海岸线与岛屿的简化结果就没有道路那么好,还需要人工检查与再编辑;境界线次之。主要原因是自然要素的边界无规律可循,节点环境非常复杂,而人文要素边界规律性较强,节点环境相对较简单。
4) 根据图 8和表 4,深度简化的结果与人工的简化结果最接近,优于道格拉斯与ArcGIS弯曲简化所获得的结果。
本文提出了一种深度简化方法,该方法将简化过程剥离成数个子过程,每个子过程通过弯曲识别与分类,并利用不同的阈值组合来处理弯曲。试验证明,该方法充分考虑了线要素的制图因子——线宽,并针对不同比例尺、不同类型的对象都有很好的简化效果。同时,相比于其他简化方法,该方法的简化结果更接近于人工处理结果,基本实现了以计算机为主、人工为辅的目标,提高了制图效率。
为了进一步减少人工参与,提高要素尤其是自然要素简化的满意度,本文后续将会尝试对三级甚至更高级的弯曲进行分类与处理。
| [1] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. Canadian Cartographer, 1973, 10(2):112-122. |
| [2] | TONG X, XU G. A New Least Squares Method Based Line Generalization in GIS[J]. International Geoscience and Remote Sensing Symposium, 2004(5):2912-2915. |
| [3] | LI Z L. OPENSHAW S. Linear Feature's Self-adapted Generalization Algorithm Based on Impersonality Generalized Natural Law[J]. Translation of Wuhan Technical University of Surveying and Mapping, 1994(1):49-58. |
| [4] | 朱鲲鹏,武芳,王辉连,等. Li-Openshaw算法的改进与评价[J]. 测绘学报,2007,36(4):450-455. |
| [5] | 黄志坚,张金芳,徐帆江. 关键点检测的线要素综合算法[J]. 中国图象图形学报,2012,17(2):241-248. |
| [6] | 艾廷华,郭仁忠,刘耀林. 曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报,2001,30(4):343-348. |
| [7] | 毋河海. 数字曲线拐点的自动确定[J]. 武汉大学学报(信息科学版),2003,28(3):330-335. |
| [8] | 罗广祥,祝国瑞,毋河海,等,坐标单调分析下地图曲线弯曲识别模型的研究[J],测绘通报,2005(10):21-24. |
| [9] | 郭庆胜,黄远林,章莉萍. 曲线的弯曲识别方法研究[J]. 武汉大学学报(信息科学版),2008,33(6):596-599. |
| [10] | 操震洲,李满春,陈亮. 曲线弯曲的多叉树表达[J]. 测绘学报,2013,42(4):602-607. |
| [11] | 黄博华,武芳,崔仁健,等. 保持弯曲特征的线要素化简算法[J]. 测绘科学技术学报,2014,31(5):533-537. |