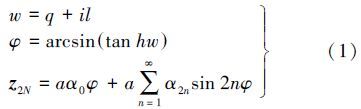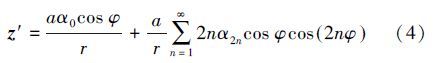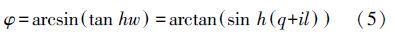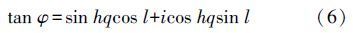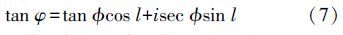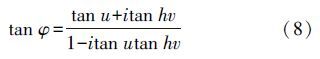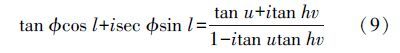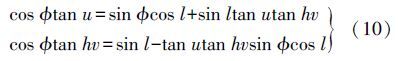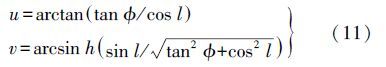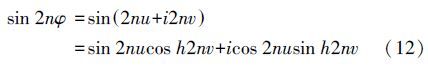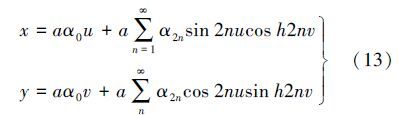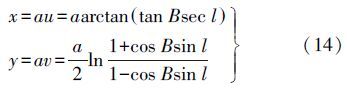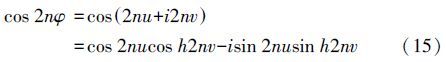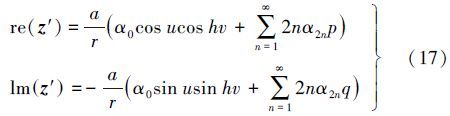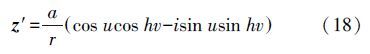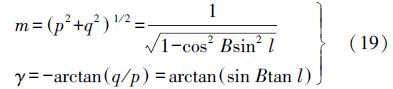2. 海军驻天津地区航保军事代表室, 天津 300042
高斯投影作为大地测量常用的一种投影,被国内外学者广泛研究。如文献[1-4]中借助黎曼-柯西方程给出了高斯投影的实数型幂级数展开式,这种展开式形式在我国大地测量中被广泛应用,但是由于其被表示为经差的幂级数形式,因此该公式的适用范围仅限于一条很窄的条带内。由于复变函数在解决等角映射问题中具有得天独厚的优势,因此国内外学者常借助复变函数进行等角投影研究,如文献[5-11]采用不同方法推导出了高斯投影的复变函数表示,并将其表示成地球椭球第一或第三偏心率的形式,该形式适用于不同的参考椭球,并使得投影不受限于狭窄的条带内,具有“不分带”的优势。可以说,将复变函数应用于高斯投影研究中,已取得卓有成效的成果。
然而,被表示为复变函数表达式的高斯投影公式形式上虽然非常简洁,但因式中包含复数变量,导致结果不够直观且难以直接对其进行代数分析。鉴于此,本文将借鉴文献[9-11]中的方法,利用双曲 正弦函数及其与三角函数的关系,进而将高斯投影复变函数表示式等价变换为实数形式。经变换得到的实数型公式仍然具有复变函数公式的“不分带”优势,且表示结果将更直观,便于直接应用及后续分析。
一、高斯投影复变函数表示 1. 高斯投影复数公式
在利用复变函数求解高斯投影坐标的问题中 ,可将等号左边子午线弧长S向复数域开拓而得高斯投影复数坐标 z=x+iy,等号右边由等量纬度q开拓至复数等量纬度w=q+il,而等角纬度$\phi $复数开拓至复数等角纬度φ,最终得到高斯投影正解复变函数表示式。在文献[9]中,它一般表示为复数等角纬度倍角的正弦和形式,如下
式中,系数α2n参见文献[8]。 2. 长度比及子午线收敛角复数公式在对高斯投影进行性质分析时,必然要推导出对应的长度比及子午线收敛角公式。借助复变函数来求解高斯投影问题时,尺度比和子午线收敛角就是解析函数在某点处的导数。有
式中,r=NcosB;N为卯酉圈曲率半径。根据长度比及子午线收敛角的定义可知,长度比为该导数的模,而子午线收敛角为该导数幅角的反向,即将式(1)代入式(2),则式(2)最终可表示为
式中,系数α2n同式(1)。 二、高斯投影实数表示1. 高斯投影实数公式
在式(1)中,高斯投影公式被表示为复数等角纬度φ的表达式,为将投影公式表示为实部与虚部分开的形式,可将复数等角纬度φ表示成实部与虚部分开的形式,即令φ=u+iv。
将式(1)中第2个方程作如下等价变换
对式(5)两边分别取正切,并利用双曲正弦和函数的关系,可得
又根据文献[9]中可知,等量纬度q与等角纬度$\phi $存在关系式sin hq=tan$\phi $,进而可得关系式cos hq=$\sqrt{1+{{\sinh }^{2}}q}=\sqrt{1+{{\tan }^{2}}\phi }$=sec$\phi $,将这两个关系式代入式(6),则式(6)中可消去等量纬度q,等价转换为
又根据双曲函数与三角函数的关系式
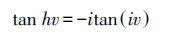
将式(7)、式(8)进行联立,可得
经化简,令式(9)中等号两边实部与虚部对应相等,可分别得实部及虚部对应关系为
求解该方程组,略去推导过程,可得
至此,已将复数等角纬度φ表示成实部与虚部分开的形式。
根据双曲函数与三角函数的关系式sin hv=-isin iv,cos hv=cos iv,则得
因此,则方程组(1)的第3个方程可表示为实部和虚部分开的形式,其中实部x为高斯投影纵坐标,虚部y为高斯投影横坐标
综上,已将高斯投影公式表示为实部与虚部分开的形式。
特别的,当地球第一偏心率e=0时,即系数α2n=0 n≥1 ,根据反双曲正弦的定义及其对应的对数表达式,则高斯投影公式简化为
由文献[12]可知,当地球椭球的第一偏心率e=0时,基于高斯投影复变函数公式推导出的“不分带”实数坐标公式(14)与文献[12]中给出的公式完全相同,该特例在一定程度上验证了本文推导的高斯投影实数型“不分带”公式的正确性。
2. 长度比及子午线收敛角实数公式
根据双曲函数与三角函数的关系式sin hv=-isin iv,cos hv=cos iv,则得
略去推导,令cosφcos 2nφ的实部与虚部分别为p和q,经过化简可得
将式(15)、式(16)代入式(4),则式(4)可最终表示为实部与虚部分开的形式
至此,已推导出长度比及子午线收敛角公式的实数公式。
特别的,当地球第一偏心率e=0时,即系数α2n=0 n≥1 ,根据反双曲正弦的定义及其对应的对数表达式,则高斯投影公式简化为
因此,高斯投影的长度比及子午线收敛角公式的实数公式分别为
由文献[13]可知,当地球椭球的第一偏心率e=0时,利用高斯投影复变函数公式推导出的“不分带”实数型长度比及子午线收敛角公式(19)与文献[13]中的公式相同,该特例一定程度上验证了长度比和子午线收敛角实数型“不分带”公式的正确性。
三、算例分析
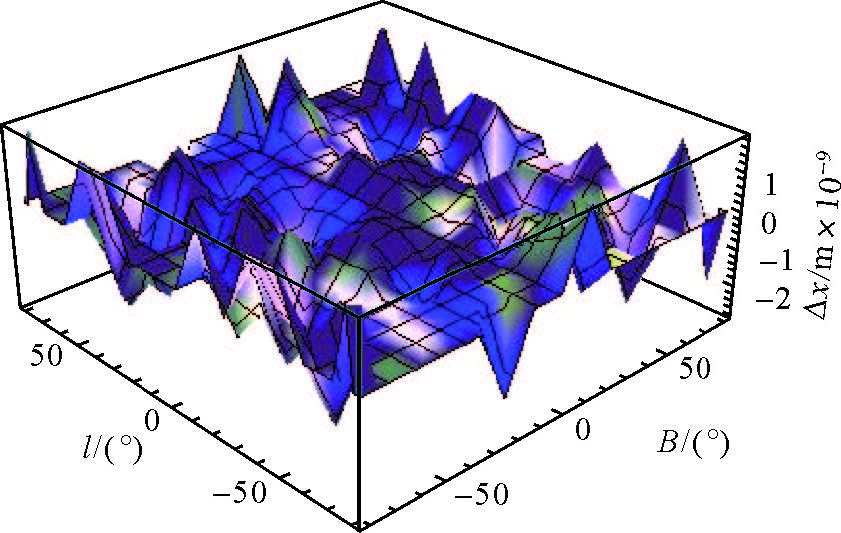
为验证本文推导公式的正确性,将其与高斯投影复变函数表示式进行比较。以CGCS2000椭球(长半轴a=6378137m,扁率f=1/298.257222101)为例,取展开至e10的高斯投影公式,记x1、y1、m1、γ1分别为借助实数公式推导出的纵坐标、横坐标、长度比及子午线收敛角;x2、y2、m2、γ2分别为借助复数公式推导出的纵坐标、横坐标、长度比及子午线收敛角;令Δx=x1-x2,Δy=y1-y2,Δm=m1-m2,Δγ=γ1-γ2,可借助计算机代数系统[14-15]分别绘制出在P={ B,l : l ≤80°,B ≤80°}范围内,Δx、Δy、Δm、Δγ的变化趋势图,分别如图 1-图 4所示,其中Δx、Δy的单位为m,Δm的单位为1,Δγ的单位为角秒。
|
| 图 1 实数和复数公式计算的高斯纵坐标差异 |
|
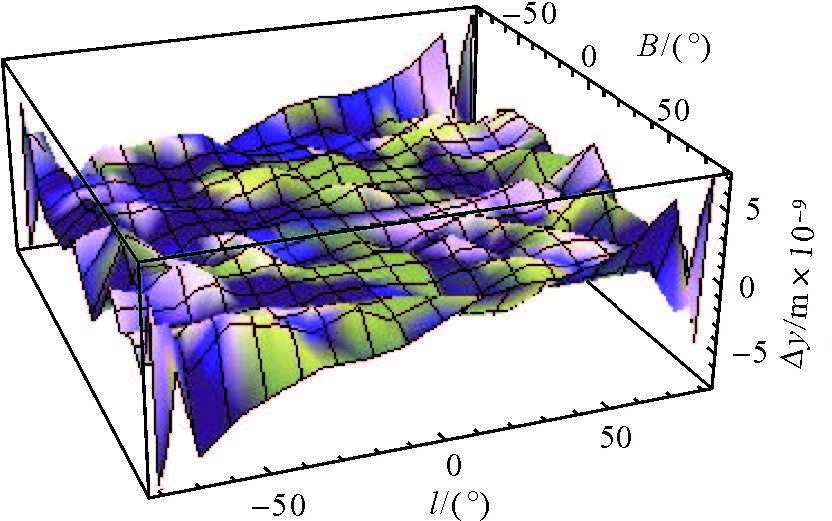
| 图 2 实数和复数公式计算的高斯横坐标差异 |
|
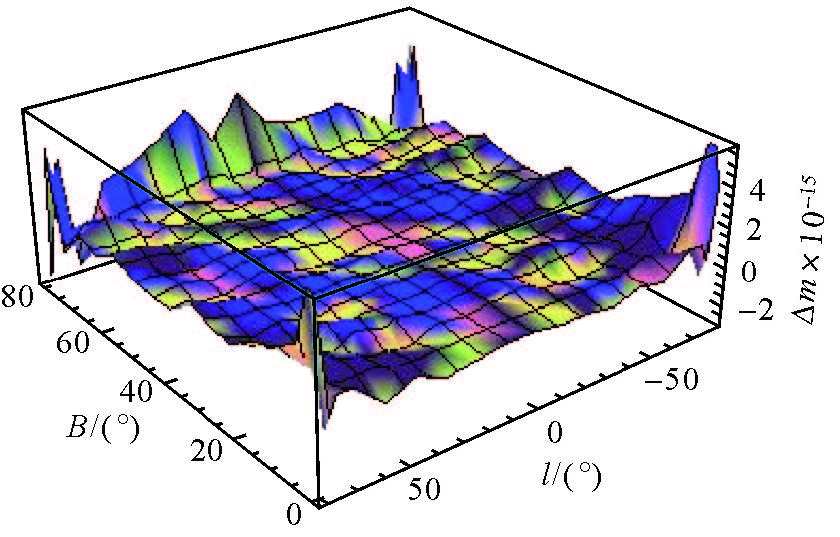
| 图 3 实数和复数公式计算的高斯投影长度比差异 |
|
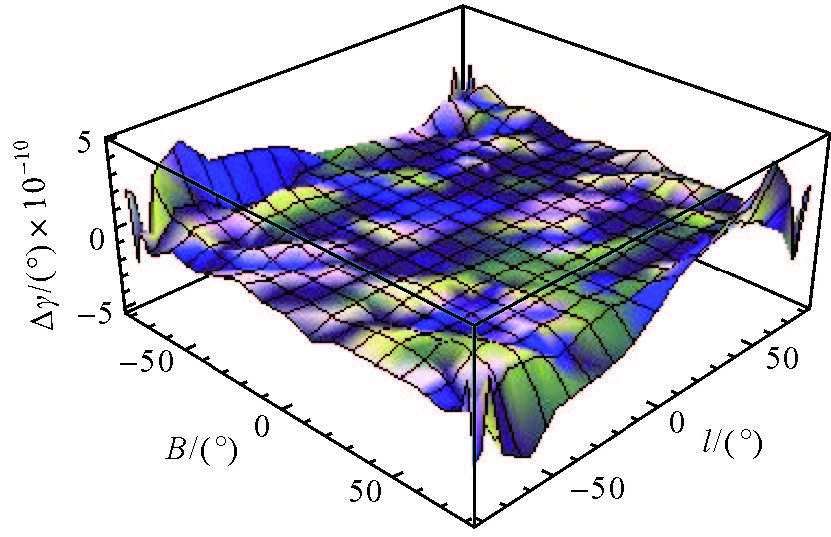
| 图 4 实数和复数公式计算的子午线收敛角差异 |
由图 1、图 2可以看出,在P={ B,l : l ≤80°,B ≤80°}范围内,利用高斯投影实数型“不分带”公式与利用高斯投影复变函数公式计算的坐标间差异绝对值均小于10-8m,其中,纵坐标差异在-3×10-9~2×10-9m范围内,横坐标差异在-7×10-9~7×10-9m范围内。考虑到计算机代数系统本身存在的计算误差,可得出结论:利用以上两种公式计算的高斯坐标完全相同,经变换后的高斯投影实数型“不分带”坐标公式与高斯投影复变函数坐标公式是等价的,即该算例验证了本文推导的实数型“不分带”坐标公式的正确性。
由图 3、图 4可以看出,在P={ B,l : l ≤80°,B ≤80°}围内,利用高斯投影实数型“不分带”公式与利用高斯投影复变函数公式计算的差异为:长度比差异在-4×10-15~5×10-15范围内,子午线收敛角的差异在-5×10-10″~5×10-10″范围内。考虑到计算机代数系统本身存在的系统误差,可得出结论:利用以上两种公式分别计算的长度比及子午线收敛角完全相同,经变换后的高斯投影长度比及子午线收敛角实数型“不分带”公式,与高斯投影长度比及子午线收敛角复变函数表示式是等价的,即该算例验证了本文推导的实数型“不分带”长度比及子午线收敛角公式的正确性。
综上,高斯投影实数型“不分带”公式具有与复数公式相同的运算结果,即本文基于高斯投影复变函数表示式推导高斯投影实数型“不分带”公式的过程是等价变换,以上两个算例验证了该推导过程的正确性。
四、结 论本文通过借助双曲正弦和公式、双曲函数与三角函数间的函数关系,经过一系列变换,将高斯投影复变函数表示式等价变换为实数形式,并借助计算机代数系统验证了该实数公式的可靠性,得出如下结论:
1) 与高斯投影复变函数表示式相比,本文推导出的实数型公式同样具有“不分带”的优点,且表示结果更直观、了然,便于直接应用及后续的研究分析。
2) 本文推导出的高斯投影实数型“不分带”公式,在一定程度上完善了高斯投影理论,丰富了地图投影数学基础。
3) 由于复变函数在解决等角问题中具有得天独厚的优势,可进一步借助双曲函数及其与三角函数间的变换关系,实现由复数公式到实数公式的等价转换,这种思路在解决类似等角问题具有较好的应用前景。
| [1] | 杨启和. 地图投影变换原理与方法[M]. 北京: 解放军出版社, 1989. |
| [2] | 熊介. 椭球大地测量学[M]. 北京: 解放军出版社, 1988. |
| [3] | YANG Q H, SNYDER J P, TOBLER W R. Map Projection Transformation: Principles and Applications[M]. London: Taylor&Francis, 2000. |
| [4] | SNYDER J P. Map Projections-A Working Manual [M]. Washington D C: Government Printing Office, 1987. |
| [5] | 边少锋, 张传定. Gauss 投影的复变函数表示[J]. 测绘学院学报, 2001,18(3): 157-159. |
| [6] | 李厚朴, 边少锋. 高斯投影的复变函数表示[J]. 测绘学报, 2008, 37(1): 5-9. |
| [7] | BIAN S F, LI H P. Mathematical Analysis in Cartography by Means of Computer Algebra System[C]//Carlos Bateira. Cartography-A Tool for Spatial Analysis. Croatia: InTech, 2012. |
| [8] | 李厚朴. 基于计算机代数系统的大地坐标系精密计算理论及其应用研究[D]. 武汉: 海军工程大学, 2010. |
| [9] | BOWRING B R. The Transverse Mercator Projection-A Solution by Complex Numbers[J]. Survey Review, 1990, 30(237): 325-342. |
| [10] | BERMEJO M, Otero J. Simple and Highly Accurate Formulas for the Computation of Transverse Mercator Coordinates from Longitude and Isometric Latitude [J]. Journal of Geodesy, 2009(83):1-12. |
| [11] | KARNEY C F F. Transverse Mercator with an Accuracy of a Few Nanometers[EB/OL].[2015-05-01]. http://geographiclib.sf. net/tm.html. |
| [12] | 孙达, 蒲英霞. 地图投影[M]. 南京: 南京大学出版社, 2005. |
| [13] | 刘强, 边少锋, 李忠美. 球面高斯投影及其变形的闭合公式[J]. 海军工程大学学报, 2015, 27(1): 45-49. |
| [14] | 边少锋, 许江宁. 计算机代数系统与大地测量数学分析[M]. 北京: 国防工业出版社, 2004. |
| [15] | BIAN S F, CHEN Y B. Solving an Inverse Problem of a Meridian Arc in Terms of Computer Algebra System[J]. Journal of Surveying Engineering, 2006, 132(1): 153-155. |