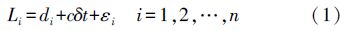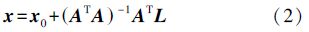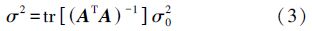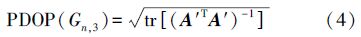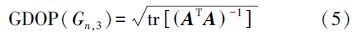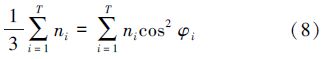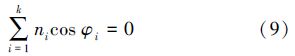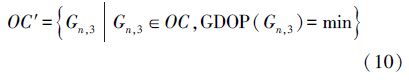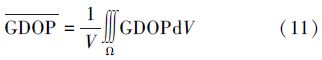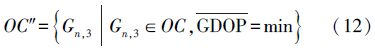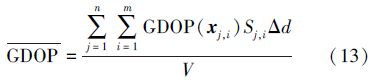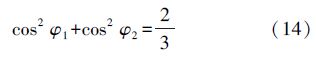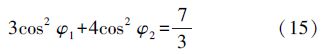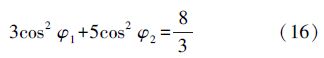在水下定位中,信号在水介质中的传播可近似看成球面波,通过在水面布设多个GNSS浮标构成浮标阵列,测量信号从水下目标点到达不同定位浮标的时间,依据伪距测量原理,实现水下定位。定位的准确性和可靠性是评价水下定位系统性能的重要依据。可靠性与冗余观测量和定位构型有关,准确性则由几何精度因子(GDOP)与测距精度共同决定。在测距精度和控制点数目固定的情况下,定位图形的GDOP越小,定位精度越高[1]。
几何精度因子是衡量定位构型优劣的重要指标[2],与控制点的空间分布和数目相关,由定位图形决定。传统的定位构型多局限于正多边形或正四面体等单一图形,文献[3]给出了具有丰富几何结构的圆锥构型、笛卡儿构型、Walker构型等最小GDOP三维定位图形。文献[4]设计了非线性伪距观测方程的雅克比矩阵A (满足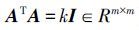 ),来最小化GDOP。
),来最小化GDOP。
对于任意给定的水下定位浮标数目n(n≥4),由单圆锥定位构型扩展的一类嵌套圆锥定位构型可满足最小GDOP。但是由于水下定位浮标均需布设于同一水平面而导致共面约束,在由定位浮标和水下目标点构成的定位图形中,其GDOP达不到理论最小值。在该约束条件下需要对嵌套圆锥图形进行二次优化来实现GDOP最小化。本文提出用GDOP密度来衡量浮标阵列的定位能力。为了实现嵌套圆锥构型GDOP最小化,嵌套圆锥构型的二次优化问题可分解为3步:①对于给定的浮标数目n,通过对n进行整数分解可构造不同的浮标组合;②基于嵌套圆锥构型最小PDOP的极值条件,在PDOP取得最小的前提下,改变圆锥张角,寻找每组浮标组合嵌套圆锥构型GDOP密度最小的局域最优解,缩小问题的可行域;③从候选的所有浮标组合构型中寻找GDOP密度最小的全局最优解。最后分别以6~8枚浮标为例,给出它们水下定位浮标阵列的最佳嵌套圆锥构型。
一、水下测距单点定位构型GDOP极值条件 1. 水下定位GDOP
在水面布设多个定位浮标以构成浮标阵列Θ=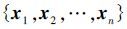 ,由水面定位浮标和水下目标点构成的定位图形可记为
,由水面定位浮标和水下目标点构成的定位图形可记为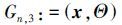 。根据GNSS伪距测量原理,其观测方程为[5]
。根据GNSS伪距测量原理,其观测方程为[5]
式中,Li为第i个浮标xi至待定点x间的伪距;di=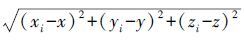 ,为欧氏距离,(x,y,z)为水下目标点x的位置坐标,(xi,yi,zi)为第i个浮标xi的空间坐标;δt为钟差;c为水介质中信号传播的平均速度;εi表示其他误差因素的等效距离误差。
,为欧氏距离,(x,y,z)为水下目标点x的位置坐标,(xi,yi,zi)为第i个浮标xi的空间坐标;δt为钟差;c为水介质中信号传播的平均速度;εi表示其他误差因素的等效距离误差。
式(1)的最小二乘解为
式中,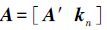 ,为非线性伪距观测方程的设计矩阵,也称雅克比矩阵;
,为非线性伪距观测方程的设计矩阵,也称雅克比矩阵;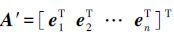 ,kn=[1 …1]T;ei=[ci,1-x1ci,2-x2…ci,m-xm ]/
,kn=[1 …1]T;ei=[ci,1-x1ci,2-x2…ci,m-xm ]/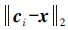 ,为待定点x至第i个已知点xi的方向余弦。
,为待定点x至第i个已知点xi的方向余弦。
水下定位的中误差为
式中,σ02为单位权方差,与测量精度有关;tr()为求矩阵的迹。假设对不同定位浮标的测量精度一致,且测量统计值相对独立,则当无钟差参数时,PDOP为水下测距单点定位构型的位置精度因子,可定义为[3, 6]
当考虑钟差因子影响时,GDOP为水下测距单点定位构型的几何精度因子,可定义为[4]
2. GDOP极值条件由式(3)可知,水下定位的精度由两个因素决定:一个是单位权方差σ02,它由伪距测量精度、浮标坐标精度等因素确定;另一个是与未知参数协因数阵有关的GDOP,它由定位浮标的几何结构决定。水下测距单点定位构型的位置精度因子PDOP取极小值,等价于[4]
式中,n为控制点的数目;3表示定位构型的维数;I为单位矩阵。当且仅当
时,几何精度因子GDOP取得极小值。
当式(6)与式(7)同时成立时,可推导出3种最小GDOP三维测距单点定位构型,包括圆锥构型、笛卡儿构型、Walker构型,其中Walker构型因其良好的对称性和均匀覆盖性已被GPS星座设计所采用。
二、嵌套圆锥构型浮标阵列优化在水下定位中,由于圆锥构型的结构更易于使定位浮标布设在同一水平面上,本文采用圆锥构型来优化浮标阵列。
1. 嵌套圆锥构型
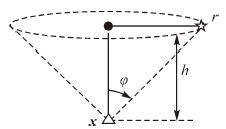
如图 1所示,x为水下目标点,h 表示目标点距离水面的深度,φ表示单圆锥定位构型的圆锥张角,r为圆锥的底面半径。由式(6)可知,当圆锥张角φ为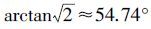 时,在顶点x处PDOP取得最小值,但此时顶点处的GDOP趋于无穷大。为解决此问题,如图 2所示,单圆锥定位构型需扩展为嵌套圆锥构型。
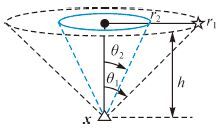
时,在顶点x处PDOP取得最小值,但此时顶点处的GDOP趋于无穷大。为解决此问题,如图 2所示,单圆锥定位构型需扩展为嵌套圆锥构型。
|
| 图1 单圆锥构型 |
|
| 图2 嵌套圆锥构型 |
对于给定的浮标数目n,通过对n进行整数分解可构造出不同浮标组合的嵌套圆锥构型,可记为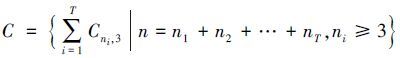 ,如n=9,可分解为9=3+6、9=4+5或9=3+3+3。寻找每组浮标组合嵌套圆锥构型GDOP的最小值则需要研究嵌套圆锥构型最小GDOP的极值条件。
,如n=9,可分解为9=3+6、9=4+5或9=3+3+3。寻找每组浮标组合嵌套圆锥构型GDOP的最小值则需要研究嵌套圆锥构型最小GDOP的极值条件。
若嵌套圆锥定位构型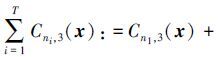 Cn2,3(x)+…+CnT,3(x)满足条件方程[3]
Cn2,3(x)+…+CnT,3(x)满足条件方程[3]
则GDOP取得极值的条件方程式(6)成立,此时在嵌套圆锥构型的顶点处PDOP取得最小值;当且仅当
时,条件方程式(7)成立,此时,在嵌套圆锥构型顶点处GDOP取得最小值。
2. 共面约束的嵌套圆锥构型
由于水下定位浮标均需布设于同一水平面,即圆锥张角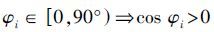 ,导致共面约束,即式(9)不成立。由定位浮标和水下目标点构成的嵌套圆锥定位图形,其GDOP达不到理论最小值。在该约束条件下需要对嵌套圆锥图形进行二次优化来实现GDOP最小化。
,导致共面约束,即式(9)不成立。由定位浮标和水下目标点构成的嵌套圆锥定位图形,其GDOP达不到理论最小值。在该约束条件下需要对嵌套圆锥图形进行二次优化来实现GDOP最小化。
寻找满足PDOP最小的嵌套圆锥构型,可记为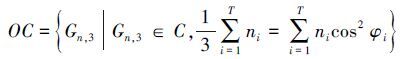 。条件方程式(8)为一不定方程,当T>1时,一般存在无穷多解。通过改变圆锥张角,可构造出无穷多个满足最小PDOP但不同结构的嵌套圆锥图形。从中寻找一组GDOP最小的解即为固定浮标组合嵌套圆锥构型GDOP最小的局域最优解。因此,嵌套圆锥构型最小GDOP的优化问题可记为
。条件方程式(8)为一不定方程,当T>1时,一般存在无穷多解。通过改变圆锥张角,可构造出无穷多个满足最小PDOP但不同结构的嵌套圆锥图形。从中寻找一组GDOP最小的解即为固定浮标组合嵌套圆锥构型GDOP最小的局域最优解。因此,嵌套圆锥构型最小GDOP的优化问题可记为
从候选的所有浮标组合构型中寻找GDOP最小的一组即为共面约束条件下嵌套圆锥构型GDOP最小的全局最优解。
为考察定位浮标对水下区域的定位性能并讨论圆锥构型覆盖区域最佳定位构型,本文引入GDOP密度来衡量水下定位浮标阵的区域定位能力。对于给定的三维空间区域Ω,GDOP密度定义为
式中,dV为体积微元,用于考察三维空间区域中的GDOP密度。GDOP密度的最佳浮标阵列优化问题可记为
上述优化问题在定义积分区间后,可使用数值积分方法实现。
三、实例分析假设定位目标区域为一球体,如图 3所示,半径R为100 m,目标区域中心点处水深为200 m。将球由内向外分为n=200个同心球,相邻两个同心球之间的半径差Δd=0.5 m,并把每个球表面分成m=1280个三角微元,则式(11)可记为
|
| 图3 目标球体球表面三角微元 |
式中,GDOP(xj,i)为第j个球面上的第i个三角网重心处的GDOP;Sj,i为第j个球面上的第i个三角网的面积;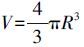 ,为目标区域的体积。
,为目标区域的体积。
为简化定位构型结构,下面分别以布设6~8枚浮标,分布在嵌套着两个单圆锥的图形上为例(ni表示第i个圆锥上浮标数),研究其水下定位浮标阵列的最佳嵌套圆锥构型。
1. n=6当浮标平均分布在两个嵌套的圆锥上,记C3,3(x)+C3,3(x),由嵌套圆锥定位构型的极值条件式(8)可推出
根据式(14)可知 ,则
,则 35.3°。
35.3°。
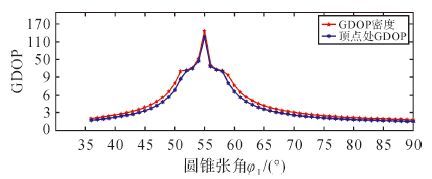
式(14)表明第2个圆锥的圆锥张角φ2随着φ1在35.3°≤φ1≤90°的范围内变化,由图 4可得:
|
| 图4 C3,3(x)+C3,3(x) 的GDOP |
1) 目标区域中心点处GDOP随着圆锥张角φ1的变化趋势与整个区域的GDOP密度变化趋势一致。
2) 当两个圆锥重合,即两个圆锥张角φ都为54.7°时,嵌套圆锥构型变为单圆锥定位构型,定位区域中心点处的GDOP与整个区域的GDOP密度都达到最大值。
3) GDOP密度随着圆锥张角φ1的变化而变化,在φ=54.7°的左侧单调递增,在φ值的右侧单调递减,在φ1的左右端点处的GDOP密度相等。因此,整个区域的GDOP密度最小值在φ1的端点处取得。
2. n=7对于嵌套圆锥组合C3,3(x)+C4,3(x),由式(8)可推出
根据式(15)可知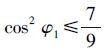 ,则
,则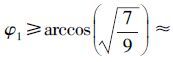 28.1°。
28.1°。
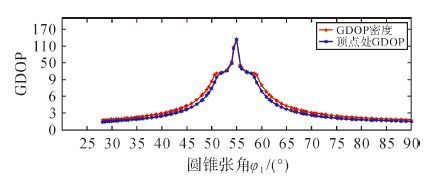
图 5表示C3,3(x)+C4,3(x)浮标组合嵌套圆锥构型的GDOP随圆锥张角φ1的变化趋势,由图 5可得:
|
| 图5 C3,3(x)+C4,3(x)的GDOP |
1) 图 5与图 4在单调性、最值问题上相似,并进一步证明了嵌套圆锥构型顶点处GDOP最小等价于整个区域的GDOP密度最小。
2) 当浮标在两个圆锥上分布不相等时,GDOP在左右端点处的值也不相等,圆锥张角φ1取最小值时GDOP达到最小。
3) 图 5 中GDOP密度的最小值小于图 4中 GDOP密度的最小值,说明嵌套圆锥定位构型GDOP的最小值随着浮标个数的增加而变小。
3. n=8当浮标个数n=8时,对n进行整数分解为8=3+5或8=4+4,因此有两个不同的嵌套圆锥组合C3,3(x)+C5,3(x)和C4,3(x)+C4,3(x)。
对于嵌套圆锥组合C3,3(x)+C5,3(x),由式(8)可得
根据式(16)可知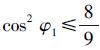 ,则
,则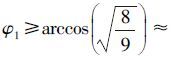 19.5°。由嵌套圆锥定位构型的极值条件可知嵌套圆锥组合C4,3(x)+C4,3(x)的GDOP与n=6时C3,3(x)+C3,3(x)组合的GDOP一致。
19.5°。由嵌套圆锥定位构型的极值条件可知嵌套圆锥组合C4,3(x)+C4,3(x)的GDOP与n=6时C3,3(x)+C3,3(x)组合的GDOP一致。
如图 6所示,可得以下结论:
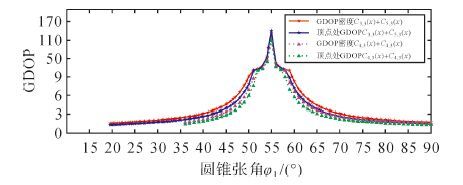
|
| 图6 C3,3(x)+C5,3(x) 和C4,3(x)+C4,3(x) 的GDOP |
1) 相同圆锥张角的构型中,浮标组合C4,3(x)+C4,3(x)的GDOP比C3,3(x)+C5,3(x)组合的GDOP小。
2) 在嵌套圆锥组合C3,3(x)+C5,3(x)上取得GDOP密度最小的全局最优解,此时,φ1=19.5°,φ2=90°,GDOP=1.485;而在嵌套圆锥组合C4,3(x)+C4,3(x)上只能取得GDOP密度最小的局域最优解,此时,φ1=35.3°,φ2=90°,GDOP=1.578。
四、结论在水下定位中,嵌套圆锥构型的结构更易于定位浮标的布设,然而由于共面约束,定位构型的GDOP达不到理论最小值,为此,需要对嵌套圆锥构型进行二次优化来寻找最小GDOP。为简化构型结构,本文对嵌套着两个单圆锥的定位构型进行了研究,得出以下结论:
1) 目标区域中心点处GDOP最小等价于整个区域的GDOP密度最小,表明可用目标区域中心点代替整个目标区域进行最小GDOP定位构型优化研究。
2) 对于给定的浮标数目n,通过对n进行整数分解可构造不同组合的嵌套圆锥构型,每一个浮标组合构型都存在一个GDOP最小的局域最优解。当在两个圆锥上浮标分布满足1∶2时,嵌套圆锥构型GDOP最小的全局最优解在该分布上取得;当浮标个数不能满足1∶2分布时,GDOP最小的全局最优解在近似1∶2分布上取得。
3) 对于浮标组合固定的嵌套圆锥构型,GDOP随着两个圆锥张角差值的增大而变小。当考虑定位信号在水中的折射率时,最佳圆锥张角依据信号折射的截止角进行调整,如截止角为10°,定位浮标个数为6时,嵌套圆锥定位构型GDOP全局最优解将由φ1=35.3°,φ2=90°调整为φ1=37.1°,φ2=80°。
4) 在水下定位的实际应用中,依据本文内容,根据给定的浮标数目可以快速给出最优浮标组合及最佳圆锥张角,并结合实测水深,确定浮标的布设半径。
| [1] | SHARP I, YU K, GUO Y J. GDOP Analysis for Positioning System Design[J]. IEEE Transactions on Vehicular Technology, 2009, 58(7):3371-3382. |
| [2] | YARLAGADDA R, ALI I, AL-DHAHIR N, et al. GPS GDOP Metric[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(5):259-264. |
| [3] | 薛树强, 杨元喜. 最小GDOP测距单点定位构型的一种嵌套圆锥结构[J]. 武汉大学学报(信息科学版),2014,39(11):1369-1373. |
| [4] | 薛树强, 杨元喜, 陈武,等. 正交三角函数导出的一类最小GDOP测距单点定位构型解集[J]. 武汉大学学报(信息科学版),2014,39(7):820-825. |
| [5] | 党亚民,秘金钟,成英燕.全球导航卫星系统原理与应用[M].北京:测绘出版社,2007. |
| [6] | 万军,党亚民,王川阳,等.最小几何精度衰减因子定位图形研究进展[J].测绘科学,2015,40(12):73-76. |
| [7] | LEVANON N. Lowest GDOP in 2-D Scenarios[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000,147(3):149-155. |
| [8] | 蔡艳辉, 程鹏飞.差分GPS水下定位系统的解析法网形分析[J].武汉大学学报(信息科学版),2008,33(8):324-327. |
| [9] | 杨元喜. 动态定位自适应滤波解的性质[J]. 测绘学报, 2003,32(3):189-192. |
| [10] | XUE S, YANG Y, DANG Y, et al. Dynamic Positioning Configuration and Its First-order Optimization[J]. Journal of Geodesy, 2013,88(2):127-143. |
| [11] | YANG Y, LI J, XU J, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011,56(26):2813-2819. |
| [12] | 李建文,李作虎,周巍,等.卫星导航中几何精度衰减因子最小值分析及应用[J].测绘学报,2011,40(S1):86-88. |
| [13] | PHILLIPS A H. Geometrical Determination of PDOP[J]. Navigation,1984,31(4):329-337. |
| [14] | 冯遵德,卢秀山,郭英.测距空间交会测量模式中交会图形优劣的诊断[J].测绘通报,2004(12):24-26. |
| [15] | 高扬.同时顾及精度和可靠性准则的控制网优化设计[J]. 测绘学报,1987,16(3):232-239. |