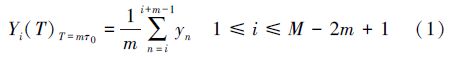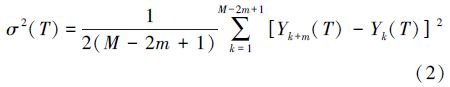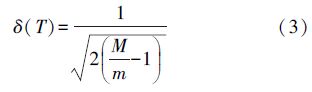,
,
,
北斗卫星导航定位系统(BDS)自2012年正式运行以来，已经在交通运输、灾害监测及电力调度等方面发挥着重要作用[1-2]。目前大部分的精密定位算法都是基于观测噪声为高斯白噪声的前提条件下进行参数解算。但是大量研究表明，GPS观测噪声并不服从这一假设，实际观测数据中还含有大量有色噪声和未模型化的误差，这将严重影响GNSS定位精度与收敛速度[3-5]。
目前关于GPS噪声特性分析已经有许多相关性的研究，如极大似然估计 [6-8]、Allan方差[4, 9-11]等。由Allan提出的Allan方差法是一种时域分析方法，现已广泛应用于INS与GNSS数据处理 [12-14]。文献[4]分析得出了GPS非差观测值的随机模型特性，其噪声组成为WM+GM，并得出了具体噪声参数的数值。BDS系统由于其独特的星座属性，区别于GPS的频谱分布，不同的接收机硬件属性，使其噪声特性较GPS有一定的区别。本文利用交叠式Allan方差，采用iGMAS高频数据，通过大量试验对比分析了BDS与GPS观测噪声成分，得出了具体的噪声参数，分析了可能产生的原因。
一、Allan方差基本原理Allan方差反映了噪声在时域上的不稳定性，它不仅能够分析数据的噪声成分，而且还可以求解出相应的噪声参数，其中的交叠式Allan方差在相同的置信水平下比普通Allan方差分析方法具有更大的置信区间，是对Allan方差的一种改进[15]。假定数据序列有M个数据点，采样率为τ，交叠式Allan方差计算过程如下：
1) 构造数组。根据交叠式分组规律，将样本空间{y1,y2,…,yM}依次按照每m个数据分成一组，得到数组[14]。
2) 求平均值。根据式(1)计算每一组序列的平均值Yi(T)，其中T=mτ，得到随机变量Yi(T)的序列
3) 计算方差。计算相应的交叠式Allan方差，计算公式如下
4) 改变T值。通过改变m值，使T不断变化，重复步骤1)—3)，得到不同T对应的方差值。
5) 构造曲线图。在双对数坐标系中构造σ(T)～T 曲线，称为Allan方差曲线。
不同噪声具有不一样的特性，这些都会反映在σ(T)～T曲线的斜率上，根据Allan方差图中曲线斜率判断相应的噪声类型，再根据相应的特征点提取相应的参数(见表 1)。
| 噪声类型 | Allan方差 | 噪声参数 | 斜率 | 参数取值 |
| 白噪声(WN) | 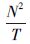 | N | 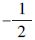 | N=σ(1) |
| 闪烁噪声(FN) |  | B | 0 | B=σ(f0) |
| 随机游走(RW) | 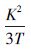 | K | 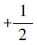 | K=σ(3) |
| 一阶马尔可夫过程(GM) | 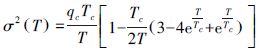 | Tc,σGM |  |  |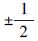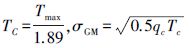
Allan在实际运用中利用一组有限的数据来分析数据的时间序列关系，其精度随着m的增加而减小，IEEE标准给出的Allan方差的计算误差公式为[15]
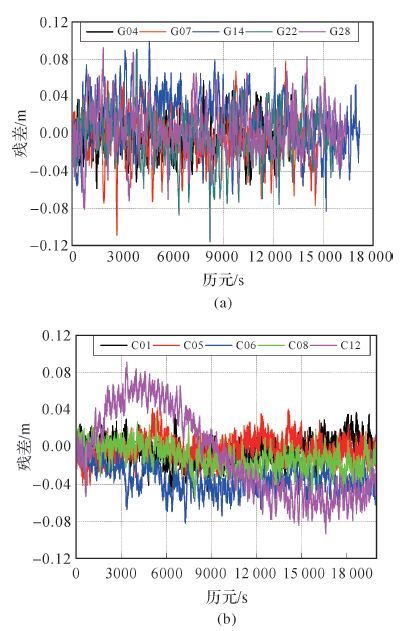
二、相位残差序列分析
在GNSS精密单点定位中，一般默认为观测值噪声满足高斯白噪声特性，然而实际操作中由于观测对象、手段、仪器设备、环境等的影响，存在各种有色噪声，如果不考虑这些非白色噪声部分，将会影响状态参数的估计。本文选取了iGMAS中8个测站2015年中年积日为71 d的1 Hz的高频数据，截止高度角为10°，采用PPP模式进行单站单天解算，输出GPS与BDS卫星相位验后残差数据，数据预处理标记并剔除残差序列中的粗差，选取其中XIA1站GPS与BDS各5颗卫星为代表，其相位残差序列及Allan方差噪声特性分析如图 1、图 2所示。
|
| 图1 XIA1站GPS与BDS部分卫星相位残差序列 |
|
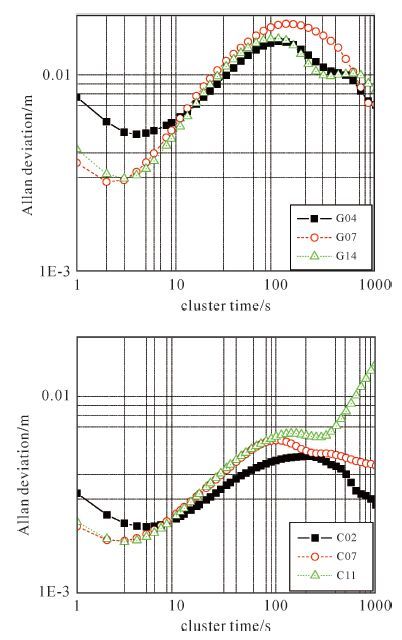
| 图2 GPS与BDS部分卫星相位残差的Allan方差 |
XIA1站部分卫星相位验后残差如图 1所示。由文献[2-3]可知，不同的数据长度对WN、FN、RW影响较小，不影响其特征分析，且GPS的GM时间相关性约为53 s，序列长度在18 000以上时可以满足本文的数据要求。
GPS验后残差序列变化平稳，没有表现出明显的趋势项。BDS卫星IGSO(C06、C08)与GEO(C01、C05)卫星相位残差与GPS卫星相当，MEO(C12)卫星的残差较大，且与高度角变化的趋势项相同。
以XIA1站部分GPS与BDS卫星相位残差序列为例，其Allan方差对数如图 2、表 2所示。对比相应的Allan方差特征(见表 1)，从图中可以看出GPS与BDS卫星相位残差噪声类型相一致，都为白噪声与一阶马尔可夫过程的叠加，但是具体特征点差异较大。
| PRN | WN | GM | |
| TC/s | σGM/mm | ||
| C01 | 2.48 | 67.72 | 1.65 |
| C02 | 1.93 | 56.61 | 1.31 |
| C03 | 1.5 | 80.42 | 0.91 |
| C04 | 3.08 | 80.42 | 1.28 |
| C05 | 2.69 | 56.61 | 1.3 |
| C06 | 1.46 | 67.72 | 1.89 |
| C07 | 1.44 | 56.61 | 1.82 |
| C08 | 2.04 | 67.72 | 1.69 |
| C09 | 1.56 | 56.61 | 1.51 |
| C10 | 1.83 | 67.72 | 2.19 |
| C11 | 1.65 | 67.72 | 1.93 |
| C12 | 1.49 | 80.42 | 1.62 |
| C13 | - | - | - |
| C14 | 1.56 | 47.6 | 21.7 |
以北斗C07卫星为例，在高频段Allan方差图BDS斜率约等于-1/2，根据表 1可以判断出为白噪声，在T=1处取得特征值2.18×10－3，即N=2.18 mm，数据序列长度为20 000，计算误差为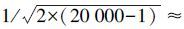
0.5%。在中频段BDS的Allan方差图斜率近似为±0.5，由此可以判断噪声类型为一阶马尔可夫过程。在最高点T=101±2处得到最大值σ=5.96×10－3，由表 1公式计算可得
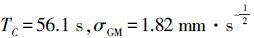，计算误差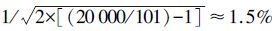
。 北斗卫星的具体结果见表 2，其中13号卫星因为故障原因没有观测数据。
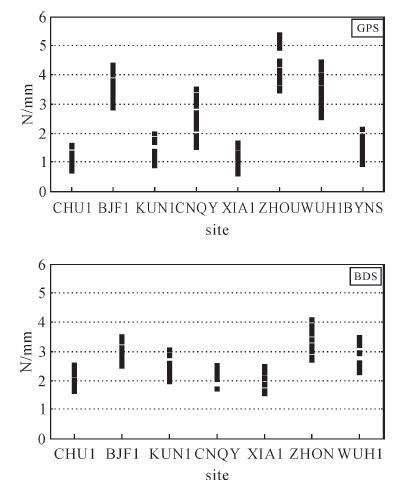
对所有测站观测到的所有GPS与BDS卫星的相位残差的Allan方差进行统计分析，其中，对白噪声参数以测站分类，对一阶马尔可夫过程按照卫星号进行分类，统计结果如图 3、图 4所示，其中BYNS测站由于北斗卫星观测数少于4颗无法定位，故只有GPS数据。
|
| 图3 各测站GPS与BDS的WN参数 |
|
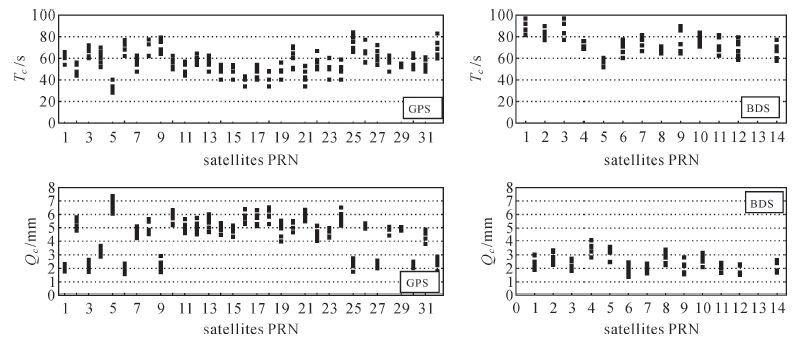
| 图4 GPS与BDS卫星的GM参数 |
从图中可以看出，白噪声参数与各测站相关性高，这说明白噪声的产生与测站接收机和观测环境有很大关系；一阶马尔可夫过程与卫星相关性大，这说明误差产生原因与卫星端有关，具体原因尚不明确，有可能是受未被参数准确估计的对流层残余、电离层二阶项及卫星钟漂等的影响。
同一测站，GPS与BDS的白噪声没有明显的联系，不同测站接收机与观测环境对GPS与BDS的影响有较大区别，这直接反映在不同测站的GPS与BDS白噪声的大小关系上，且同一系统不同测站间差异较大，如CHU1与ZHON站GPS的白噪声差异达到3 mm左右。横向对比多个测站可以发现，BDS白噪声的变化波动小于GPS的变化波动，全部集中在2.5~4.2 mm之间，GPS分散在0.5~5.5 mm间。相比于GPS，BDS各卫星的GM过程的相关时间TS明显要大，Qc较小，且各个卫星之间差异较小，这可能与北斗卫星运动的角速度慢有关[5]。
统计各个测站与各卫星噪声参数值如图 5、图 6和表 3所示。从图表中可以看出，iGMAS大部分测站的相位白噪声在2.5 mm左右，方差在0.6 mm以内，BDS的白噪声参数绝对值与方差都稍大于GPS，所有测站GPS与BDS的WN均值分别为2.33、2.50 mm；方差分别为0.50、0.53 mm。相应的GM过程，BDS的相关时间明显大于GPS，其中MEO卫星的时间相关性明显小于其他种类卫星，相应的GPS与BDS的GM过程噪声分别为4.43、2.38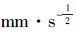 
；相关时间分别为55.51、71.07 s。
|
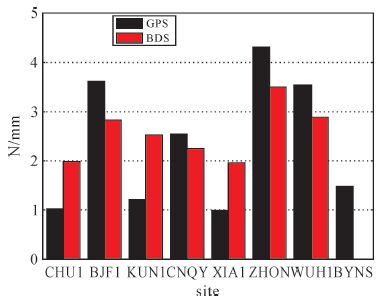
| 图5 各测站GPS与BDS的WN参数统计 |
|
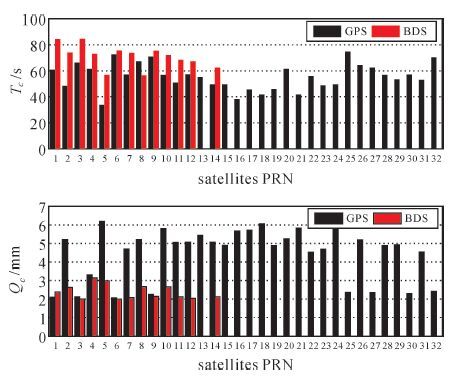
| 图6 各测站GPS与BDS的GM参数统计 |
| 系统 | WN | GM | ||||
| N | Var | Ts | Var | Qc | Var | |
| GPS | 2.33 | 0.5 | 55.51 | 10.1 | 4.43 | 1.36 |
| BDS | 2.5 | 0.53 | 71.07 | 8.55 | 2.38 | 2.36 |
综合上述信息可以得出，相位观测值噪声为白噪声与一阶高斯马尔科夫过程噪声的叠加，不是简单的白噪声，参数估计需要重新考虑观测值的随机模型。
四、结论正确的随机模型是一切平差的基础，同时也可以为BDS随机模型提供近似的先验值，提高解算精度，加快收敛速度。本文采用iGMAS实测数据，利用交叠式Allan方差法经过大量试验对比分析了GPS与BDS相位噪声差异。结果表明：
1) BDS与GPS观测数据噪声成分一样，都为WN+GM的组合；观测数据噪声为高斯白噪声的假设明显是不准确的。
2) BDS与GPS白噪声值较为接近，分别为2.33，2.50 mm，且方差也基本相同；不同测站间BDS白噪声变化波动小与GPS。
3) BDS与GPS的GM过程噪声参数相差较大，BDS的相关时间为77.07 s，明显大于GPS 55.51 s的相关时间；过程噪声为2.38 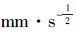，明显小于GPS 4.43 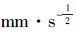的过程噪声。
| [1] | 中国卫星导航系统管理办公室. 北斗卫星导航系统发展报告2.2[M]. 北京:[s.n.],2013. |
| [2] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1):1-6. |
| [3] | Rankin J. An Error Model for Sensor Simulation GPS and Differential GPS[C]//Position Location and Navigation Symposium, 1994, IEEE.[S.l.]:IEEE, 1994:260-266. |
| [4] | 张小红,朱锋,薛学铭,等. 利用Allan方差分析GPS非差随机模型特性[J]. 测绘学报, 2015,44(2):119-127. |
| [5] | 宋超, 精密单点定位快速收敛技术与方法研究[D]. 郑州:信息工程大学, 2015. |
| [6] | 黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2):31-33. |
| [7] | 李昭, 姜卫平, 刘鸿飞,等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4):496-503. |
| [8] | 廖华, 徐锐, 陈维锋,等. 汶川地震前后四川区域GPS时序特征演变及统计分析[J]. 地球物理学报, 2013, 56(4): 1237-1245. |
| [9] | NIU X, CHEN Q, ZHANG Q, et al. Using Allan Variance to Analyze the Error Characteristics of GNSS Positioning[J]. GPS Solutions, 2014, 18(2):231-242. |
| [10] | FRENDERICHS T. Analysis of Geodetic Time Series Using Allan Variances[D]. Stuttgart: University of Stuttgart, 2010. |
| [11] | 薛学铭. Allan方差分析测量数据噪声特性的性能研究[J]. 大地测量与地球动力学, 2014,34(6):131-134. |
| [12] | ALLAN D W. Statistics of Atomic Frequency Standards[J]. IEEE Proceedings, 1996, 54(2):221-230. |
| [13] | RILEY W J, RILEY W J. Handbook of Frequency Stability Analysis[J]. NIST SP-1065, 2007, 1065:1-123. |
| [14] | 李晓莹, 胡敏, 张鹏,等. 交叠式Allan方差在微机械陀螺随机误差辨识中的应用[J]. 西北工业大学学报, 2007, 25(2):225-229. |
| [15] | IEEE 1139. Definitions of Physical Quantities for Fundamental, Frequency and Time Metrology-Random Instabilities[S].[S.I.]: IEEE Standard Board, 2008. |