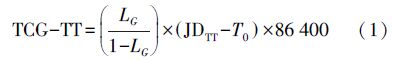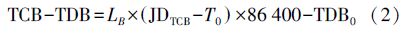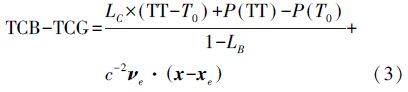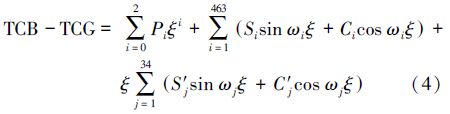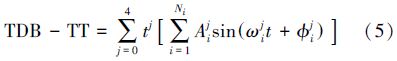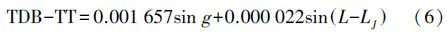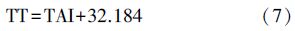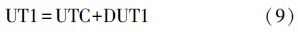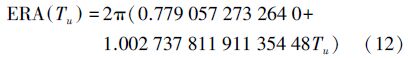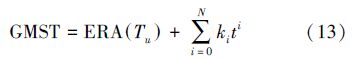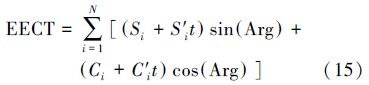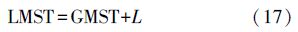2. 中国科学院上海天文台,上海 200030
现代大地测量学中出于不同目的会采用不同的时间系统[1-15]。如各类观测资料记录时间基准为协调世界时(coordinated universal time,UTC);国际地球参考系(international terrestrial reference system,ITRS)、岁差-章动模型、轨道计算中运动积分等的时间基准均为地球时(terrestrial time,TT);国际天球参考系(international celestial reference system,ICRS)、天文历表的时间基准为质心力学时(barycentric dynamical time,TDB);计算地球自转角的时间基准为世界时(Universal Time,UT1);计算格林尼治平恒星时(Greenwich mean sidereal time,GMST)、格林尼治恒星时(Greenwich sidereal time,GST)的时间基准有UT1和TT;而TT则是由国际原子时(international atomic time,TAI)具体实现的;此外,坐标时是广义相对论框架所定义的四维时空参考系中的一个坐标量,质心天球参考系(barycentric celestial reference system,BCRS)的坐标时为质心坐标时(barycentric coordinate time,TCB),地心天球参考系(geocentric celestial reference system,GCRS)的坐标时为地心坐标时(geocentric coordinate time,TCG)。
上述时间系统虽然各不相同,但彼此之间存在内在的关联,本文拟就现代大地测量中相关时间系统的定义、应用、分类、转换关系等内容进行明确,以满足理论研究和实际计算的需要。
一、时间系统的分类根据IAU决议、IERS规范[16-17],以及美国海军天文台第179号通报对IAU决议的解释[18],目前在科学研究和工程应用中所涉及的时间系统主要分为两大类:一类是以国际单位制秒长为基准的原子时系统,另一类是以地球自转为基准的世界时系统。
1. 原子时系统定义国际单位制秒长是建立原子时系统的基础。目前国际计量局对国际单位制秒长的最新定义为[14, 19]:铯133原子基态的两个超精细能级在零磁场下跃迁辐射震荡9 192 631 770周所持续的时间。国际单位制秒长可根据定义在任意地方予以实现,其中在大地水准面上实现的国际单位制秒长称为TAI秒长。TAI是根据遍布世界各地50多个国家计时实验室按照国际单位制秒长定义制作的300多座原子钟的测量数据经加权平均得到的是目前稳定度最高、最均匀的时间系统。
出于研究太阳系天体运动的目的,1976年IAU定义了TDB和地球力学时(terrestrial dynamical time,TDT),随后在IAU 1991决议中,将TDT重新命名为TT,且同时定义了广义相对论框架下的时空统一参考系。在全局惯性参考系BCRS和局部惯性参考系GCRS中,坐标时分别为TCB和TCG。
虽然定义了TCB和TCG,但为了保持以往重要工作的连续性,IAU同意继续使用TDB和TT[16-18],因此在BCRS中用作历表和动力学方程的时间基准是TDB而非TCB,同样GCRS中的时间基准是TT而非TCG。TDB与TCB、TT与TCG之间均存在简单的线性变换关系,且在地球质心处,TDB与TT速率十分接近,而在大地水准面上,TT与TAI速率相同。
2. 世界时系统世界时系统的建立基础是UT1秒长。UT1秒长是建立在地球自转基础上且消除了极移影响后的秒长,由于受到季节性变化、潮汐摩擦等相关地球物理作用的影响,地球自转速率长期变慢,因此UT1秒长是不均匀的,这就使得稳定度极高的TAI与低稳定度的UT1之间存在不断的变化,带来使用的不便性。
为了协调TAI和UT1这两类基准不同的时间系统,引入了UTC。UTC的秒长与TAI一致,通过加入跳秒使UT1-UTC<0.9 s,使其与UT1在时刻上尽量保持一致,兼顾了地球自转变慢的效应,而UTC与TAI之间仅存在跳秒的差异。
在IERS 2010规范中[17],UT1认为是平太阳在天球中间极(celestial intermediate pole,CIP)赤道上与地球中间零点(terrestrial intermediate origin,TIO)之间的夹角,而在CIP赤道上天球中间零点(celestial intermediate origin,CIO)与TIO之间的夹角定义为地球自转角(earth rotation angle,ERA),它与UT1之间存在线性关系。CIO的位置接近ICRS的赤经零点,TIO的位置接近ITRS的零子午线方向。同样,GMST、GST分别认为是瞬时平春分点、瞬时真春分点在CIP赤道上与TIO之间的夹角,二者与ERA之间存在明确的函数关系。
上述各类世界时系统之间的关系可用图 1进行描述,由于瞬时平春分点与瞬时真春分点位置几乎相同,故而图中仅给出GST。
|
| 图1 世界时系统示意图 |
原子时系统彼此间的转换主要是基于相对论框架,而世界时系统之间的转换主要是基于地球自转和岁差-章动模型,这些转换关系由IAU决议和IERS规范所给出[16-18]。
1. TT、TCG、TDB、TCB之间的转换转换公式如下
式中,JD为儒略日;LG=6.969 290 134×10-10;T0=2 443 144.500 372 5;LB=1.550 519 768×10-8;TDB0=-6.55×10-5;LC=1.480 826 867 41×10-8;c为光速,xe、νe分别为地球质心在BCRS中的位置、速度向量,x为测站在BCRS中的位置向量,可基于天文历表计算获得;非线性部分P(TT)的最大振幅不超过1.6 ms,差项P(TT)-P(T0)可基于时间历表计算获得。
计算TCB与TCG之差除式(3)外,Harada和Fukushima[20]还给出了一个解析公式,在1600—2200年间,该公式的精度为0.4 ns,被IERS 2010规范采纳并推荐使用,即
式中,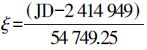 ;P0=-36.074 229 013 122 05;P1=70.048 073 545 563 13;P2=1.543 558 5×10-7;Si、Ci、S´j、C´j分别为各展开项的振幅;ωi、ωj分别为各展开项的频率。
;P0=-36.074 229 013 122 05;P1=70.048 073 545 563 13;P2=1.543 558 5×10-7;Si、Ci、S´j、C´j分别为各展开项的振幅;ωi、ωj分别为各展开项的频率。
而TDB与TT间的差值有3种计算方法,第1种方法是由天文历表(如DE、INPOP、EPM历表)计算得到;第2种方法是根据Fairhead和Bretagnon[21]发布的解析公式计算获得,即
式中,t为从J2000.0起算的儒略千年数;Aij、ωij、φij分别为各展开项的振幅、频率和初相。其结果精度优于1 ns,被SOFA程序库所采纳使用。当所需的计算结果精度不超过100 ns时,可采用只展开至127项的简化解析式进行计算。后来Irwin[22]发布了包含1075个展开项的精密解析式,以期获得0.1 ns的计算精度。
当精度要求不高时,可采用Urban[23]给出的近似计算公式获得
式中,g、L、LJ分别为地球平近点角、太阳平黄经、木星平黄经,三者的计算公式见参考文献[24]。式(6)适用范围为1980—2050年间,计算精度在30 μs以内。
2. TT、UTC、TAI、UT1之间的转换转换公式如下
式中,LS在1972年之前是与MJD相关的小数,1972年之后为整数,具体数值可由IERS Bulletin C获得,也可从巴黎天文台、美国海军天文台等相关机构网站下载;DUT1的具体数值可由IERS Bulletin D获得,也可从IERS发布的EOP 08 C04模型中获得。
3. UT1与TT的转换转换公式为
ΔT的数据来源之一是美国海军天文台发布的historic_deltat.data、deltat.data、deltat.preds 3个数据文件,提供了1657—2023年间ΔT的具体数值,且定期对数据进行更新。ΔT的第2个数据来源是由IERS发布的EOP 08 C04模型中的DUT1、IERS Bulletin C中的LS数据经计算后得到
ΔT也可根据经验公式计算得到。目前常用的经验公式主要是Morrison和Stephenson给出的用多项式形式表达的一组经验公式,该组公式根据年代的不同,分别用2~7次多项式进行表达,且公式中涉及年代参数的计算公式及方法也各不相同,不便于进行程序设计。
文献[25]根据USNO发布的3个ΔT数据文件,基于最小二乘法拟合得到一组新的六次多项式经验公式,不仅适用于公元纪年、JD、MJD及从J2000.0起算的儒略世纪数等4种时间格式,便于程序设计,而且精度远高于Morrison和Stephenson公式的结果,建议在计算ΔT时使用。
4. UT1、ERA、GMST、GST、LMST、LST之间的转换转换公式如下
式中,Tu是从J2000.0起算的儒略日数,时间系统为UT1;t为从J2000.0起算的儒略世纪数;N、ki的值可从IERS 2003、2010规范中获取;Δψ、εA在IERS 2003、2010规范中[16-17],分别为相应岁差-章动模型中的元素;式(15)在两个规范中是相同的;式(18)L为测站的地理经度。
图 2为各个时间系统之间转换关系的示意图,图中箭头处括号内代表相应的转换公式。
|
| 图2 各种时间系统的转换关系图 |
根据时间系统间的转换公式,本文分别计算了1950年1月1日至2050年1月1日,时间间隔1 h的TT与TCG、TCG与TCB、TCB与TDB、TT与TDB间的差值序列;计算TCG与TCB、TT与TDB的差值时,分别采用式(4)和式(5),各差值序列及其随时间的变化如图 3所示。由于TDB与TT间的差值甚微,二者间的差值序列单独绘于图 4中。TAI与TT间差值为固定值,本文不再计算。
|
| 图3 各个时间系统间的差值序列图 |
|
| 图4 TT与TDB之间差值序列图 |
基于文献[25]计算ΔT的经验公式、IERS Bulletin C、Bulletin D、EOP 08 C04模型,本文还计算了UTC与TAI、UTC与UT1、UT1与TT间的差值序列,其中前两个差值序列的时间范围自1962年1月1日至2015年8月1日,第3个差值序列的时间范围自1950年1月1日至2015年8月1日,时间间隔均为1 h,3个差值序列及其随时间的变化也如图 3所示。
由图 3中可知,TCG与TCB、TCB与TDB间的差值序列随时间呈线性变化关系,且差值绝对值在1977年后均随时间在不断增大。而TT与TCG间的差值序列随时间虽然也呈线性变化关系,但差值的增幅相对于前两个差值序列而言则非常微小,原因在于LG的数值远小于LB、LC。同时可见UTC与TAI间的差值(跳秒)序列是不连续的,且增幅随时间在减小,这反映了地球自转不断变慢的趋势。
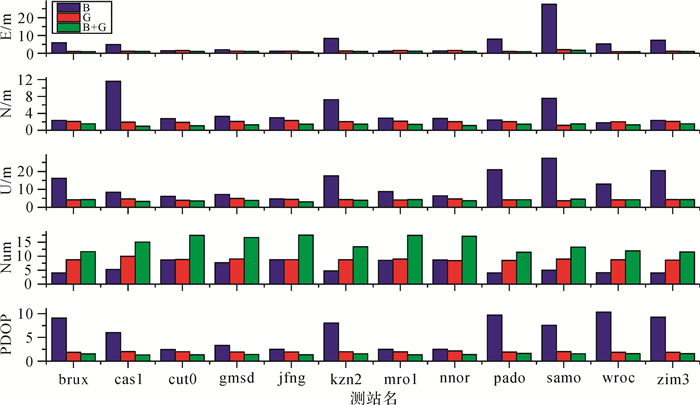
由图 4可知,TT与TDB间差值序列表现出以一年为周期的变化特征,且差值大小在1.7 ms以内,此差值在天文历表计算中可忽略不计[1-6, 26]。
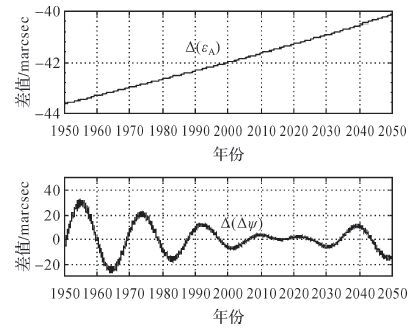
岁差-章动模型的更新带来GST计算公式的改变。为了得到GST在IERS 2003、2010规范间的差异,首先计算了岁差量εA、黄经章动Δψ在两个规范间的差值序列,分别记为Δ(εA)、Δ(Δψ)。时间范围自1950年1月1日至2050年1月1日,时间间隔为1 h,差值序列Δ(εA)、Δ(Δψ)及其随时间的变化如图 5所示。
|
| 图5 Δ(εA)、Δ(Δψ)差值序列图 |
由图 5可知,εA在两个规范间的差值序列随时间呈线性变化关系,在1950—2050年间,ΔεA在-44~-40 marcsec之间。而Δψ在两个规范间的差值序列随时间呈不规则变化关系,在1950—2050年间,Δ(Δψ)在-28~33 μarcsec之间。
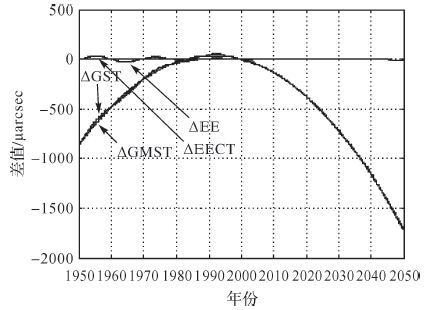
GST是由GSMT、EE、EECT计算得到的。本文计算IERS 2003、2010规范间四者的差值序列,分别记为ΔGST、ΔGMST、ΔEE和ΔEECT,时间范围自1950年1月1日至2050年1月1日,时间间隔为1 h,各差值序列及其随时间的变化如图 6所示。
|
| 图6 ΔGST、ΔGMST、ΔEE、ΔEECT差值序列图 |
由图 6可知,ΔEECT序列的值等于0,说明EECT在两个规范中是相同的;ΔEE序列随时间呈现不规则变化关系,在1950—2050年间,ΔEE在-27~32 μarcsec之间;而ΔGMST、ΔGST序列随时间呈类抛物线关系,在1950—2050年间,ΔGMST、ΔGST分别在-1699~37、-1711~51 μarcsec之间。
四、结束语时间系统是现代大地测量学中最基础同时也是最重要的内容之一,面对日益发展壮大的现代大地测量学,明确时间系统的定义及其转换关系对理论研究和工程实践均具有重要意义。在时间系统的转换过程中,需要理解相对论框架、天球参考系、地球自转、岁差-章动模型等天文学基本理论,时间系统间的转换结果可以根据上述内容自行计算获取,也可以参考IAU SOFA发布的程序计算获取。
| [1] | 李广宇.天球参考系变换及其应用[M].北京:科学出版社,2010:108-128. |
| [2] | 李广宇.天体测量和天体力学基础[M].北京:科学出版社,2015:14-23. |
| [3] | 漆贯荣.时间科学基础[M].北京:高等教育出版社,2006:19-35. |
| [4] | 刘佳成.新天文参考系若干问题的研究[D].南京:南京大学,2012:7-31. |
| [5] | MICHAEL F, RALF L.Space-Time Reference Systems[M].Berlin:Springer-Verlag, 2013:11-48. |
| [6] | MEEUS J.Astronomical Algorithms[M].2nd ed. Richmond Virginia:Willmann-Bell, 1999:71-75. |
| [7] | 张捍卫,马国强,杜兰.广义相对论框架中有关时间的定义与应用[J].测绘学院学报,2004,21(3):160-162. |
| [8] | 张捍卫,王志军,杜兰.完整后牛顿近似下原时与坐标时的转换[J].测绘学院学报,2004,21(2):79-81. |
| [9] | 魏二虎,李广文,畅柳.定位导航中常用时间系统的转换及教学研究[J].测绘地理信息,2013,38(2):7-10. |
| [10] | 魏二虎,李智强,殷志祥.相对论框架下时间系统转换及SOFA软件的教学应用[J].全球定位系统,2013,38(2):7-11. |
| [11] | 马高峰,陆强,郑勇.月球探测中的天文时间尺度[C]//中国宇航学会深空探测技术专业委员会第一届学术年会论文集.哈尔滨:[s.n.],2005:105-110. |
| [12] | IAU Division I Working Group "Nomenclature for Fundamental Astronomy". Explanation of the Proposed Terminology[R].NFA WG Explanatory Document B:[s.n.], 2005: 1-19. |
| [13] | 黄天衣,刘佳成.IAU2006"基本天文学术语"及其解释[R].南京:南京大学,2007:1-17. |
| [14] | Klioner S. Relativistic Scaling of Astronomical Quantities and the System of Astronomical Units[J]. Astronomy and Astrophysics, 2008, 478(3): 951-958. |
| [15] | HOHENKERK C Y. SOFA and the Algorithms for Transformations between Scales & between Systems[C]//Proceedings of the Journées 2011"Systèmes de référence spatio-temporels" (JSR2011): Earth Rotation, Reference Systems and Celestial Mechanics: Synergies of Geodesy and Astronomy. Vienna: Vienna University of Technology, 2011: 21-24. |
| [16] | DENNIS D M, GéRARD P. IERS Conventions (2003), IERS Technical Note 32[R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2004: 104-108. |
| [17] | GÉRARD P, BRIAN L. IERS Conventions (2010), IERS Technical Note 36[R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2010: 133-139. |
| [18] | GEORGE H K. The IAU Resolutions on Astronomical Reference System, Time Scales, and Earth Rotation Models Explanations and Implementation. United States Naval Observatory Circular NO.179[R]. Washington D.C:U.S Naval Observatory,2005: 7-18. |
| [19] | 马高峰,郑勇,杜兰,等.时空参考系中的坐标和时间单位[J].天文学进展,2010,28(4):383-390. |
| [20] | HARADA W, FUKUSHIMA T. Harmonic Decomposition of Time Ephemeris TE405[J]. The Astronomical Journal, 2003, 126(5): 2557-2561. |
| [21] | FAIRHEAD L, BRETAGNON P. An Analytical Formula for the Time Transformation TB-TT[J]. Astronomy and Astrophysics, 1990, 229(1): 240-247. |
| [22] | IRWIN A W, FUKUSHIMA T. A Numerical Time Ephemeris of the Earth[J]. Astronomy and Astrophysics, 1999, 348(2): 642-652. |
| [23] | URBAN E, SEIDELMNN K.Explanatory Supplement to the Astronomical Almanac[M].3rd ed.[S.l.]:University Science Books, 2013: 104-113. |
| [24] | SIMON J L, BRETAGNON P, et al. Numerical Expressions for Precession Formulae and Mean Elements for the Moon and the Planets[J]. Astronomy and Astrophysics, 1994, 282(2): 663-683. |
| [25] | 雷伟伟,李凯,张捍卫.世界时与地球时转换经验公式的改进与比较[J].飞行器测控学报,2015,34(5):552-557. |
| [26] | 谢懿,刘宇飞,邓雪梅.深空探测中不同时间的比较[C]//中国宇航学会深空探测技术专业委员会第八届学术年会论文集.上海:[s.n.],2011:628-631. |