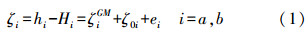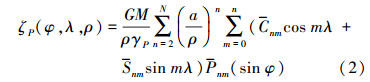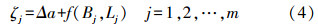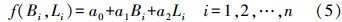2. 铁道第三勘察设计院集团有限公司测绘分院，天津 300251
,
,
高程基准由高程起算基准面和相对于该起算基准面的水准原点高程组成，可为高程测量提供统一的起算依据，一般采用区域某一验潮站或多个验潮站的长期观测数据确定的平均海水面作为国家高程起算面,我国采用1985国家高程基准，高程起算面是采用我国1952—1979年间青岛验潮站数据确定的平均黄海海水面[1]。不同的国家由于采用的验潮站及其数据资料不一样，导致国家间的高程基准不一致，这不利于全球范围内的重力场、现代地壳运动、板块运动及监测等地球科学研究，也不利于跨国工程项目的实施，因此全球或区域高程基准的统一问题始终是大地测量学的研究热点之一，目前主要采用验潮站数据、GNSS/水准数据、卫星测高数据、全球重力场模型等数据源，基于GNSS/水准法、重力边值法及重力场模型法等方法确定[2, 3, 4, 5, 6, 7, 8, 9, 10, 11]，而随着全球重力场模型精度和分辨率的逐步提高，利用重力场模型实现全球或区域高程基准统一的方法也逐步被国内外学者关注[2, 4]。本文主要探讨利用GNSS/水准数据及地球重力场模型实现高程基准统一的方法，并实现某一跨国工程的高程基准统一。计算结果表明，本文方法简单可行，在小区域范围具有较高的精度。
一、原理与方法 1. 地球重力场模型法
在图 1中，地面a和b两点处于两个不同的高程基准中，高程起算面分别是由验潮站Oa和Ob确定的平均海水面，则有
 |
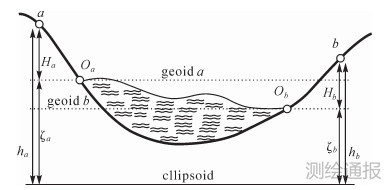| 图 1 不同高程基准示意图 |
根据Bruns公式，地球表面上任意点p的模型高程异常可由下式获得[6]
式中，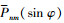
为完全规格化Legndre函数；GM为地心引力常数；N为地球重力场模型展开的最高阶数；对于超高阶Legndre函数计算要特别注意计算的稳定性，其他参数含义见文献[6]。
根据式(1)和式(2)，在每一个高程基准区域选择一定量的GNSS/水准数据即可确定各区域高程基准与重力场模型确定的全球高程基准间的基准差，也可以求得两个区域高程基准间的系统差，即可实现两高程基准统一及高程转换。
2. 基于GNSS/水准数据拟合法在由验潮站Oa确定的高程基准内(以下称为基准1)(如图 1所示)，可利用一定量的GNSS/水准数据采用一定的拟合方法建立将GNSS大地高转换为正常高的拟合模型，则有
在由验潮站Ob确定的高程基准内(以下称为基准2)，采用的拟合模型同基准1，但由于基准1和基准2间存在基准系统差，故将式(3)改为如下形式
式中，Δa为基准1和基准2间的基准差(为常数)。若取拟合模型为平面模型，则有 式中，a0、a1和a2为拟合系数。若在基准1中有n个GNSS/水准数据，在基准2中有m个GNSS/水准数据，则式(3)—式(5)可联合写为 式中，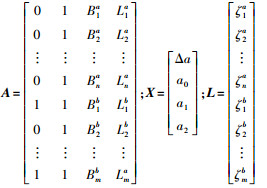
利用式(6)即可确定两个不同高程基准间的系统差，进而实现不同高程基准间的统一。为了提高参数解算的稳定性，需要对各点坐标进行归一化处理及单位换算。
二、精度分析现选择某一跨国工程勘测项目进行试验研究，该项目对应的高程基准分别为我国1985国家高程基准和波罗的海高程基准，共收集到10个GNSS/水准点，其中1985国家高程基准点有4个，波罗的海高程基准点有6个，GNSS/水准点的点位分布如图 2所示,由于GNSS成果是无约束平差结果，故大地高会存在一个系统差，但这并不影响基准统一，也不影响两高程基准间系统差的确定。
 |
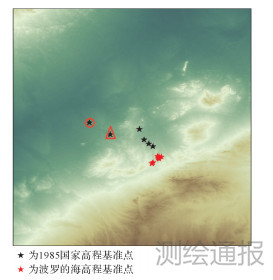| 图 2 GNSS/水准点示意图 |
选择具有代表性的EGM2008和EIGEN-6c4stat(以下简称EIGEN-6c4)超高阶重力场模型进行试验研究[6, 7, 8, 9]。其中，EGM2008是利用GRACE卫星数据(ITG-GRACE03S)、地面重力数据及卫星测高数据等数据源获得的第一代超高阶重力场模型，该模型在精度和分辨率方面均实现了质的飞跃；而EIGEN-6c4模型是利用EGM2008重力场模型数据、GRACE卫星、GOCE卫星及卫星测高等数据源获得的新一代超高阶重力场模型，由于采用了GOCE卫星数据，理论上模型在100~200阶应当比EGM2008模型具有更好的精度。利用EGM2008和EIGEN-6c4分别对基准1对应的GNSS/水准数据和基准2对应的GNSS/水准数据进行处理：首先根据式(2)利用GNSS点的大地坐标计算各点的模型高程异常；然后根据式(1)分别计算各个高程基准与重力场模型表示的高程基准间的系统差；最后将计算获得的两个高程基准系统差作差，即可获得基准1和基准2间的系统差，计算结果见表 1。由于本次试验中GNSS成果为无约束平差结果，其坐标会存在较大的系统差，但并不影响各点的相对精度，且高程异常对点的坐标不敏感，故也不影响两独立高程基准间系统差的确定。
| m | ||||||
| 高程基准 | 重力场模型 | 最小值 | 最大值 | 平均值 | 标准差 | 备注 |
| 基准1 | EGM2008 | -5.896 | -5.861 | -5.872 | 0.016 | 1985高程基准 |
| EIGEN-6c4 | -5.916 | -5.884 | -5.894 | 0.015 | ||
| 基准2 | EGM2008 | -5.539 | -5.376 | -5.409 | 0.064 | 波罗的海高程基准 |
| EIGEN-6c4 | -5.551 | -5.394 | -5.427 | 0.061 | ||
| 基准2 | EGM2008 | -5.389 | -5.376 | -5.383 | 0.005 | 粗差剔除后 |
| EIGEN-6c4 | -5.411 | -5.394 | -5.402 | 0.006 | ||
表 1结果表明，对于基准1，EGM2008和EIGEN-6c4模型都具有较高的精度，标准差分别为0.016和0.015m，两模型精度基本一致，模型确定的高程异常与GNSS/水准确定的高程异常的平均值分别为-5.872和-5.894m。对于基准2，EGM2008和EIGEN-6c4模型对应标准差分别为0.064和0.061m，经进一步分析发现有1点可能为粗差点，见图 2中画圆圈点，剔除该粗差点后，EGM2008和EIGEN-6c4模型对应的标准差分别为0.005和0.006m，两模型精度基本一致，模型确定的高程异常与GNSS/水准确定的高程异常的平均值分别为-5.383和-5.402m。理论上这些平均值即为区域高程基准与重力场模型所表示的大地水准面的差值，分析发现该值较大，很大一部分是由于大地高存在较大系统差造成的，故该平均值不具有明确的物理意义。由表 1中的各模型平均值可获得基准1和基准2间的基准差，对于EGM2008模型该基准差为0.489m，EIGEN-6c4模型该基准差为0.492m，相差约0.003m。扣除模型高程基准系统差后，基于EGM2008和EIGEN-6c4模型的整体高程转换精度分别为9.9和9.6mm。
2. 基于GNSS/水准数据拟合法利用9个GNSS/水准点(已剔除粗差)，根据式(5)建立考虑高程基准间系统差的拟合模型，一并求解高程拟合参数及高程基准间系统差，点间最长距离约24km，各点的拟合残差见表 2。
| mm | |||||||||
| 点数 | 基准1 | 基准2 | |||||||
| C8 | LS1 | C6 | LS2 | BM1 | Rp1 | Rp2 | BM2 | Rp3 | |
| 9个点 | 13.4 | -8.8 | -4.0 | -0.6 | 1.2 | 1.3 | 6.5 | -4.8 | -4.2 |
| 8个点 | 1.1 | -4.8 | 0.9 | 2.8 | 0.9 | -4.1 | 2.2 | 1.0 | — |
当选用GNSS/水准点为9个时，法方程条件数为80.0965，说明方程状态良好，解结果稳定，此时高程异常拟合残差最大值为13.4mm，最小值为-0.6mm，标准差为6.3mm(见表 2)，获得的两高程基准系统差为463.2±9.8mm。删除较远的Rp3点(图 2中三角符号点)，此时点间最长距离约18km，再进行高程拟合，法方程条件数为129.0965，说明方程状态良好，解结果稳定，此时高程异常拟合残差最大值为2.8mm，最小值为-4.8mm，标准差为2.6mm(见表 2)，获得的两高程基准系统差为462.4±4.1mm。若首先扣除由EGM2008模型获得的两基准间的系统差0.489m，再进行以上计算，则9个点和8个点计算得到两基准间的系统差分别为-25.8和-26.6mm，该结果即是由EGM2008模型确定的高程基准间的系统差与GNSS/水准拟合法确定的基准间系统差之差，各点残差与表 2结果一致。由以上结果可以看出：①两次获得的高程基准间的系统差并无明显差异，但精度差异较大，主要原因是该方法受GNSS/水准点的数量、分布、拟合模型及区域地形起伏大小等因素的影响；②考虑高程基准间系统差参数后，是否扣除模型确定的基准间系统差对高程转换结果无影响。
三、结束语本文主要研究采用EIGEN-6c4和EGM2008等重力场模型及GNSS/水准数据确定区域不同高程基准间的系统差，进而实现不同高程基准间的高程转换及基准统一，试验结果表明：
1) 采用EIGEN-6c4和EGM2008超高阶重力场模型可较好地确定不同高程基准间的系统差，在本次试验中EGM2008和EIGEN-6c4模型确定的高程基准差分别为0.489和0.492m，考虑该基准差后，EGM2008和EIGEN-6c4模型的整体高程转换精度分别为9.9和9.6mm。
2) 利用GNSS/水准数据，采用考虑高程基准间系统差的拟合模型，一并求解高程拟合参数及高程基准间系统差参数的方法同样可以获得较好结果，9个点和8个点(删除较远一个GNSS点，如图 2所示)获得的两高程基准系统差分别为463.2±9.8和462.4±4.1mm，与重力场模型确定的结果相差约2.6cm，但从统计意义讲，两种方法获得结果具有很好的符合度。
3) 鉴于地球重力场模型法使用简单，但会受模型在该区域精度影响，而GNSS/水准法同样受水准点的数量、分布、拟合模型及区域地形起伏大小等因素影响，故可将这两种方法融合，即采用移去-恢复法，理论上应当可提高解算精度。但由于本文试验区域较小，且两模型精度很高，采用该方法几乎无影响，因此未在本文中列出相应结果。
4) 综合考虑本次试验收集到的GNSS/水准点数及试验区域特点，本文只选用平面拟合法进行了相关研究，其他拟合方法效果需进一步探讨。
| [1] | 程鹏飞,成英燕,文汉江,等.2000国家大地坐标系实用宝典[M].北京:测绘出版社,2008:24-65. |
| [2] | GERLACH C, RUMMEL R.Global Height System Unification with GOCE: a Simulation Study on the Indirect Bias Term in the GBVP Approach[J]. Journal of Geodesy,2013,87(1):57-67. |
| [3] | AMOS M J, FEATHERSTONE W E. Unification of New Zealand's Local Vertical Datums: Iterative Gravimetric Quasigeoid Computations[J]. Journal of Geodesy,2009, 83(1):57-68. |
| [4] | GATTI A, REGUZZONI M, VENUTI G.The Height Datum Problem and the Role of Satellite Gravity Models[J].Journal of Geodesy,2013,87(1):15-22. |
| [5] | TENZER R, DAYOUB N, ABDALLA A.Analysis of a Relative Offset between Vertical Datums at the North and South Islands of New Zealand[J].Applied Geomatits,2013,5(2):133-145. |
| [6] | 张兴福,刘成.综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J].测绘学报,2012, 41(1):25-32. |
| [7] | 张兴福,李博峰,魏德宏,等.多类重力场模型的精度分析及联合确定GPS点正常高的方法[J].测绘学报,2013, 42(1):6-12. |
| [8] | 张兴福,刘成,王国辉,等.基于EGM2008重力场模型的GPS高程转换方法及精度分析[J].地球物理学进展, 2012, 27(1): 38-44. |
| [9] | FÖRSTE C H, BRUINSMA S L, ABRIKOSOV O, et al.EIGEN-6C4:The Latest Combined Global Gravity Field Model Including GOCE Data Up to Degree and Order 2190 of GFZ Potsdam and GRGS Toulouse[R]. [S.l.]:5th GOCE User Workshop, 2014. |
| [10] | 冯林刚,赵志军,王占政,等.GPS高程转换的严密平差算法[J].测绘通报,2012(4):44-46. |
| [11] | 张潘,余代俊,张玉刚,等.GPS高程拟合方法研究及精度对比实验[J].测绘通报,2015(9):54-56. |