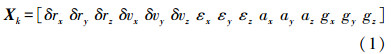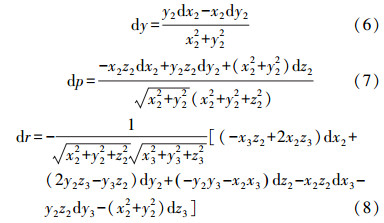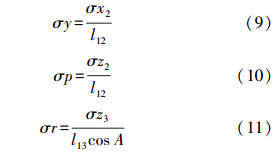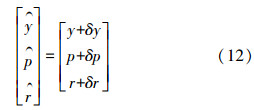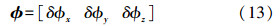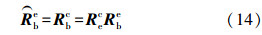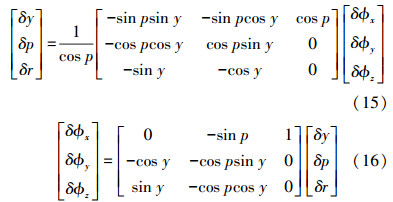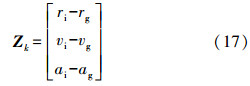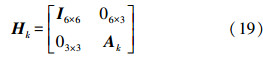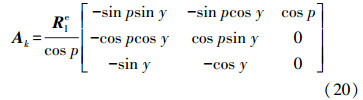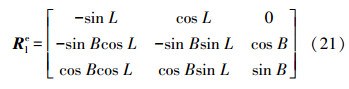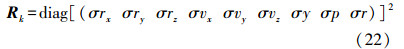2. 中国测绘产品质量检验测试中心,北京 100830;
3. 南京市城市地下管线数字化管理中心,江苏南京 210000
GPS/INS组合导航系统综合了GPS和INS的优点,同时克服了各自的缺点,已成为当今导航系统的一个重要发展方向[1]。随着GPS应用技术进一步发展,GPS多天线测量获取实时姿态已进入实用阶段[2, 3],因此在传统的位置和速度组合中加入姿态组合,可以克服传统组合方式中姿态误差及INS元件误差需要根据位置和速度等误差之间的关系来估计的缺陷,提高导航定位的精度。
许多学者在位置和速度组合的基础上提出了附加外部辅助信息测量姿态的组合方式。文献[4]提出当地水平坐标系下速度/姿态的组合方法,但没有考虑位置的组合;文献[5]提出一种姿态角更新算法,但仅适用于车载导航;文献[6, 7]提出GPS单天线测姿技术,即载体运动的情况下,由GPS观测到的载体的加速度和速度计算载体的姿态角,但由于受加速度计、陀螺仪等误差影响,得到的姿态角精度较低。
本文采用位置、速度和姿态全组合方式进行组合导航,导航坐标系选择地固系,其优点是可以直接输出地固系中载体的位置及经纬度。通过在载体上方布设3台接收机天线,利用直接法求取载体的3个姿态参数,与位置和速度共同作为观测量进行组合导航。本文介绍了全组合方式的状态模型和观测方程,推导的GPS姿态测量的误差矩阵及全组合观测噪声矩阵,利用实测的机载数据与位置和速度组合对比验证全组合方式的有效性。
一、状态方程组合导航系统选用15维系统状态参数,分别为位置误差、速度误差、平台失准角误差、加速度计偏置和陀螺仪漂移,系统状态向量为
因此,在k历元组合导航系统误差状态方程为 式中,Fk为连续系统的状态转移矩阵;Gk为系统动态噪声矩阵;Wk为系统白噪声矢量。式中符号具体表达式可参考文献[7, 8]。 二、量测方程 1. GPS测姿误差载体的姿态是指载体坐标系相对于当地水平坐标系各轴的角度关系,一般由3个姿态角确定载体的姿态[9],分别为航向角(Yaw)、俯仰角(Pitch)和横滚角(Roll)。在实际测量姿态中,一般采用直接法,GPS天线布局如图 1所示,以某个天线为基站,并视为载体坐标系原点,由此三角形确定的面为载体姿态的参考面,参考面的法向n的方向变化即为载体姿态变化。
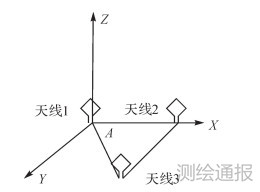 |
| 图 1 GPS天线布局 |
为计算3个姿态角,应将测得的空间直角坐标转换为以天线1为原点的载体坐标系中。假设天线2和天线3在载体坐标系的坐标分别为(x2,y2,z2)和(x3,y3,z3),则载体姿态可由直接法求出[10]
为了得到姿态角的量测误差,分别对式(3)—(5)求微分得
由式(6)—(8),可得近似的姿态测量误差为
式中,l12、l13分别为天线1到天线2和天线3的距离;A为图 1中l12和l13之间的夹角。由式(9)—(11)可知,航向角和俯仰角的精度与l12的长度成反比,横滚角的精度与l13的长度成反比,当l12与l13垂直时,横滚角的误差最小。 2. 姿态误差与平台失准角之间关系由于惯性导航元件的误差,使得惯性系统从载体坐标系到地固坐标系之间的姿态转换矩阵的计算结果产生误差δRbe,称为平台失准角[6]。由于状态方程与平台失准角有关,因此姿态组合是利用GPS观测得到的3个姿态角与INS力学编排得到的3个姿态角之间的差值,建立其与平台失准角之间的关系。姿态角可以表示为
式中,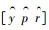 为捷联惯导系统通过力学编排得到的姿态角;[y p r]为真实姿态角;[δy δp δr]为姿态角误差。平台失准角误差可以表示为
为捷联惯导系统通过力学编排得到的姿态角;[y p r]为真实姿态角;[δy δp δr]为姿态角误差。平台失准角误差可以表示为
捷联惯导系统计算得到的姿态矩阵为
式中,R be 为载体系到地固系的坐标转换矩阵;R bc为载体系到计算坐标系的坐标转换矩阵;R ec为地固系到计算坐标系的坐标转换矩阵。具体表达式可参考文献[6]和文献[11]。将式(12)代入式(14),忽略二阶小量,可以得到姿态角误差和平台失准角之间的变换关系为
3. 全组合量测方程全组合方式选取GPS和INS各自输出的位置、速度和姿态之差作为观测量构造量测方程。假设GPS和INS在地固系中位置、速度和姿态输出分别为rg、vg、ag和ri、vi、ai,观测向量可以表示为
式(17)的误差方程为
式中,Vk为残差向量;Hk为观测矩阵;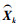 为状态向量。观测矩阵可以表示为
式中,I6×6为单位阵。由式(15)可得
式中,Rle为当地水平坐标系到地固系的坐标转换矩阵,可由载体的经度B与纬度L求得
三、试验分析
1. 全组合参数设置
为状态向量。观测矩阵可以表示为
式中,I6×6为单位阵。由式(15)可得
式中,Rle为当地水平坐标系到地固系的坐标转换矩阵,可由载体的经度B与纬度L求得
三、试验分析
1. 全组合参数设置
本文的试验数据采用北京中测新图 2011年8月25日采集的航空飞行数据,飞行时间约2.6h。飞行轨迹及使用的组合导航参数分别如图 2和表 1所示。
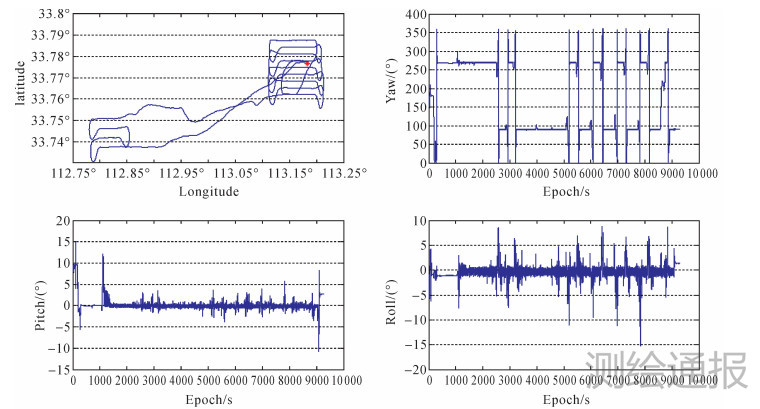 |
| 图 2 载体运动轨迹 |
| Sensos | Parameters | Accuracy |
| IMU | 采样率 | 200Hz |
| 失准角 | 0.01° 0.01° 0.03° | |
| 陀螺仪零偏 | 0.05°/h | |
| 陀螺角速率随机游走 | 0.002°/sqrt(h) | |
| 加速度计零偏 | 250ug | |
| 加速度随机游走 | 0.001m/s/sqrt(h) | |
| GPS | 采样率 | 1Hz |
| 位置测量噪声 | 0.03m | |
| 速度测量噪声 | 0.01m/s | |
| POS | 采样率 | 200Hz |
| 位置测量噪声 | 0.01m | |
| 速度测量噪声 | 0.01m/s | |
| 姿态测量噪声 | 0.003° 0.003° 0.01° |
由式(9)—式(11)可知,通常点位中误差为0.5cm,高程中误差为1cm,可以推算,对于1m的基线,航向角和俯仰角可达0.1°的精度,横滚角可达0.2°的精度,量测噪声协方差阵为
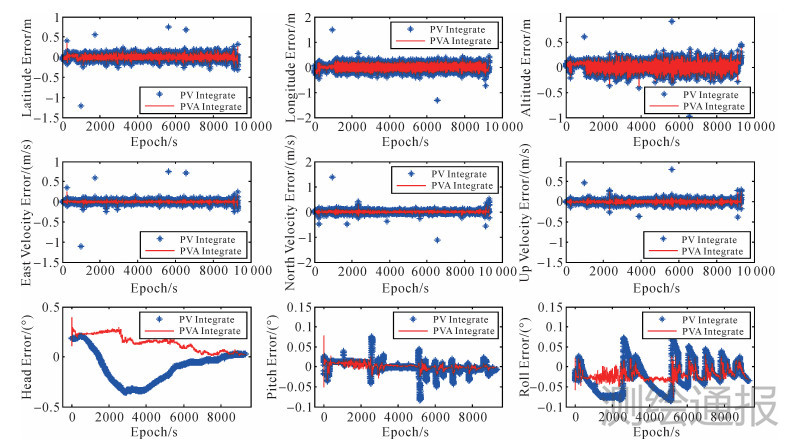
2. 试验分析本文分别使用全组合模式和位置/速度组合模式与NovAtel公司研制的Inertial Explorer软件计算得到的结果作对比,结果如图 3与表 2所示。
 |
| 图 3 两种组合方式解算误差 |
| 参数 | Position | Velocity | Attitude | |||||||
| N/cm | E/cm | U/cm | N/(cm/s) | E/(cm/s) | U/(cm/s) | Y/(°) | P/(°) | R/(°) | ||
| PV | RMS | 5.93 | 12.98 | 8.69 | 3.2 | 4.37 | 3.78 | 0.1883 | 0.0127 | 0.0461 |
| STD | 5.92 | 12.96 | 8.61 | 3.2 | 4.37 | 3.78 | 0.1608 | 0.0127 | 0.0385 | |
| PVA | RMS | 5.39 | 11.59 | 8.04 | 2.08 | 3.28 | 2.81 | 0.1625 | 0.0071 | 0.0238 |
| STD | 5.39 | 11.57 | 7.98 | 2.08 | 3.28 | 2.81 | 0.0806 | 0.007 | 0.0127 | |
| Improve | RMS | 9.11% | 10.71% | 7.48% | 35.00% | 24.94% | 25.66% | 13.70% | 44.09% | 48.37% |
| STD | 8.95% | 10.73% | 7.32% | 35.00% | 24.94% | 25.66% | 49.88% | 44.88% | 67.01% | |
由图 3可以看出,全组合模型对于姿态精度的提高非常明显,航向角一般被认为是最难估计的参数,在全组合模式下精度也得到改善。速度和位置组合的横滚角和俯仰角在飞机转弯等大机动飞行时出现大幅震荡的情况,但在全组合模式中横滚角和俯仰角受到的影响较小,这是由于引入了GPS的姿态信息,使得系统的可观测性得到了改善,不受载体的飞行轨迹影响,从而提高了姿态角的精度。速度精度也有较大的提高,并且没有出现某些历元解算出现跳变。这说明姿态组合对于组合导航系统数据有一定的平滑作用,增强了系统的稳定性。
由表 2的统计结果也可以看出,全组合模式对姿态精度改善最大,横滚角和俯仰角的RMS和STD都提高了40%以上,虽然航向角的RMS变化不是很明显,但其STD变小,说明结果更加平滑。由于姿态角精度的改善,3个方向的速度精度也有一定程度的提高,但位置精度几乎没有变化,主要原因是为了简化计算,在状态模型中忽略了一些次要的误差项,如GPS位置误差等。另外,对系统噪声和观测噪声的统计特性缺乏足够的了解也抵消掉了一部分提高的精度。
四、结束语本文在传统GPS/INS位置和速度组合的基础上增加了姿态观测,通过推导GPS与INS量测姿态之间的差值与平台失准角之间的关系,给出了位置、速度和姿态全组合的量测方程,分析了GPS的测姿精度,并由此给出量测噪声协方差阵。以商业软件IE的解算结果作为参考,全组合方案相对于传统的位置和速度组合姿态角和速度精度有了较大改善,位置精度几乎没有变化。
| [1] | YANG Y. Tight Coupled MEMS INS/GPS Integration with INS Aided Receiver Tracking [D]. Calgary: University of Calgary, 2008. |
| [2] | 刘新明, 赵李健. 一种GPS测姿系统的设计及精度分析[J]. 中国惯性技术学报, 2013, 21(1): 77-79. |
| [3] | TEUNISSEN P J G, GIORGI G, BUIST P J. Testing of a New Single-frequency GNSS Carrier Phase Attitude Determination Method: Land, Ship and Aircraft Experiments [I]. GPS Solutions, 2011, 15(1): 15-28. |
| [4] | 蒋庆仙. 关于MEMS惯性传感器的发展及在组合导航中的应用前景[J]. 测绘通报, 2006(9): 5-8. |
| [5] | 吴富梅, 聂建亮, 何正斌. 低成本车载GPS/INS组合导航姿态角更新算法[J]. 中国惯性技术学报, 2000, 18(6): 675-679. |
| [6] | 项冬. 高精度机载INS/GPS组合导航关键算法研究[D]. 北京:中国测绘科学研究院, 2013. |
| [7] | SHIN E. Estimation Technique for Low-cost Inertial Navigation [D]. Calgary: University of Calgary, 2005. |
| [8] | 何晓峰. 北斗/微惯导组合导航方法研究[D]. 长沙: 国防科技大学, 2012. |
| [9] | 田增山, 胡小川, 刘丽川. GPS姿态测量系统基线长度和天线布局设计[J]. 电波科学学报, 2001, 9(3): 379-383. |
| [10] | 赵建虎, 刘经南, 周丰年. GPS测定姿态方法研究[J]. 武汉测绘科技大学学报, 2000, 25(4): 353-357. |
| [11] | 董绪荣. GPS/INS组合导航定位及其应用[M]. 长沙:国防科技大学出版社, 1998. |